Влияние эластичного элемента при посадке тарели на седло клапана бурового поршневого насоса

Развитие техники и технологии бурения скважин требует постоянного совершенствования буровых насосных установок. Надежность насоса зависит от ресурса уплотнительных устройств гидравлической части и в значительной степени определяется сроком службы его важнейших органов: клапанов, долговечность которых при давлениях 16-18 МП и не превышает 100 часов. Такая долговечность клапанов не удовлетворяет требованиям бурения. Поэтому в настоящее время задача увеличения срока службы в среднем до 200-300 часов остается не решенной. Обеспечение бесперебойной работы буровых насосов – сложная научно-техническая задача. В настоящее время в мировой практике применяются самые различные конструкции клапанов буровых насосов (рис. 1).

Рис. 1. Конструкции клапанов отечественного и зарубежного производства

а) схема клапана: 1 – седло; 2 – тарель; 3 – уплотнительное кольцо; 4 – прижимная втулка; 5 – упорная гайка; 6 – крестовина; 7 – хвостовик; 8 – ограничитель подъема; б) в сборе; в) в разборе

Рис. 2 Предлагаемый клапан.

Клапанные устройства, используемые в буровых насосах, отличаются: 1) конструкцией уплотнительного элемента, местом его установки, 2) способом закрепления, 3) конструкцией опор и направляющих.

Авторами предлагается новая конструкция клапана бурового насоса (рис. 2).

Существенным отличием данной конструкции является то, что представленная форма уплотнительного элемента, обеспечивает улучшенную посадку. Выполнение данного вида уплотнения позволяет обеспечить взаимозаменяемость, сэкономить расход материалов и повысить технико-экономические показатели насоса.

При работе бурового клапана при определенных условиях происходит ударная посадка клапана на седло – ударные волны передаются на корпус насоса, что может иметь негативные последствия при работе бурового насоса.

Для определения максимальных усилий, передающихся на корпус насоса и их частот колебаний после удара, проведено моделирование удара тарели клапана бурового насоса при ее посадке на седло (рис. 3, а, б, в, г) заменой тарели и седла эквивалентными стержнями круглого сечения (рис. 3, б, в).

Еще академик Мандельштам отмечал, что трудно сказать, что лучше моделирует удар двух стержней: сплошная или дискретная модель [1]. В данном случае тарель и седло (массами m и m соответственно – рис. 3, б) заменяются двумя объектами, массами m ₁ (седла) и m ₂ (тарели), соединенными невесомыми пружинами (коэффициенты жесткости: с ₁ – тарели;

с ₂ – седла) - (рис. 3, г).

Примем, что m = m / 3; m = m / 3 [2].

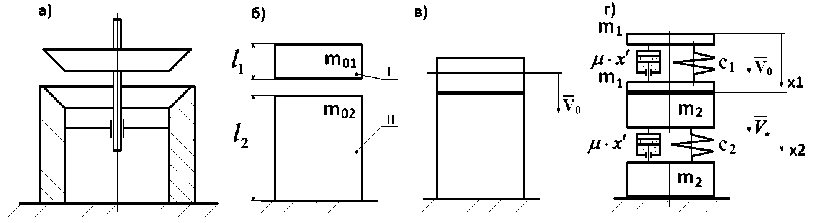
Рис. 3. Моделирование удара тарели бурового клапана о седло.

Дифференциальные уравнения, описывающие движение рассматриваемых масс после удара следующие:

m • x‘ = -ci • (xi - x2) - ц- (x‘ - x2)

(m + m2) • x" = -e2 • x2 + c • (Xj - x2) - ц • x‘ + ц • (x‘ - x‘), где xt, x2 - координаты объектов, массами mx и m2 соответственно (рис. 3, г); x‘', x‘ - их скорости;

µ - коэффициент сопротивления.

Начальные условия системы дифференциальных уравнений (1) следующие:

x io = x 20 = 0, x ‘ 0 = V o ; x 20 = V , = m • V o /( m + m 2 ) .

Скорость V определена из условия сохранения импульса: m _i • V_o = ( m _i + m ₂) • V , ; V , = m _i • V_o/(m_i + m ₂) .

Коэффициенты жесткости С₁, С₂ определялись в первом приближении следующей формулой [3]:

c ~ E • 5 /l,      (2)

где E – модуль упругости Юнга соответствующего стержня; S – площадь поперечного сечения стержня; l – длина стержня.

Массы m_x , m₂ определялись следующей формулой: m = 5 • l • p /3 ,   (3)

где ρ – плотность соответствующего стержня; S – площадь поперечного сечения соответствующего стержня; l – длина соответствующего стержня.

Принимая материалы тарели и седла одинаковыми (сталь), при равных площадях поперечного сечения S стержней I, II (рис. 3, б) отношения коэффициентов жесткости:    с / с ₂ = l ₂ / l_x = n ; отношения масс:

m / m = l ₂ / 4. Тогда система дифференциальных уравнений (1) преобразуется к следующему виду: m • x ’ = - c • ( x - x ₂) - ц • ( x - x ‘ )

(n +1) • m • x” = -(с / n) • x2 + c • (x - x2) - ц • x‘ + ц • (x‘ - x‘), (4)

где xio = x2o = o, x’o = V>; x2o = V.= m^Vo/(mi + m2) = V,/(1 + n)

Определим порядок величин: с , с ₂, m_x , m ₂ .

Пусть E = 2.1 • 10¹¹ H / м ²; 5 = 2o • io - ⁴ м ² (для обоих стержней: тарели и седла); p = 7874 кг / м ³; l_x = 2 • io² м . Тогда, c = E • 5 / l_x = 2 • io^io HI м . Масса стержня, эквивалентного тарели: m_t = p • 5 • l / 3 ^ o.io5 кг .

Решение системы дифференциальных уравнений показало, что величина скорости V не влияет на период колебаний T после удара.

На рис. 4 представлены зависимости максимальных усилий передаваемых на корпус ( F = с ⋅ x – а) и их частот (б) в зависимости от коэффициента n .

Величины реальных ударных сил, передающихся на корпус бурового насоса могут отличаться от полученных (рис. 4, а ), но порядок этих величин все равно составляет несколько тысяч Ньютон (сотни кг).

Порядок величин частот усилий, передаваемых на корпус насоса (рис. 4, б ), полученных вышеприведенным моделированием совпадает с приведенными в технической литературе (50-20 кГц) [4–7], что подтверждает правильность предыдущего моделирования.

Для снижения величин максимальных усилий, передающихся на корпус насоса, предложено установить между седлом и корпусом насоса эластичный элемент. Этот элемент с одной стороны работает как пружина, уменьшая величину усилий, передающихся на корпус насоса; с другой стороны, в этом элементе происходит демпфирование колебаний, т.е. необходимо подобрать такие материалы для эластичного элемента, чтобы выполнялись два условия: эффективная виброизоляция и демпфирование удара.

На рис. 5, а показано расположение эластичного элемента, предназначенного для уменьшения максимальных величин усилий, передающихся на корпус насоса, между седлом и корпусом насоса. Предполагается, что при работе клапана бурового насоса не происходит разъединения (отскока) седла от эластичного элемента.

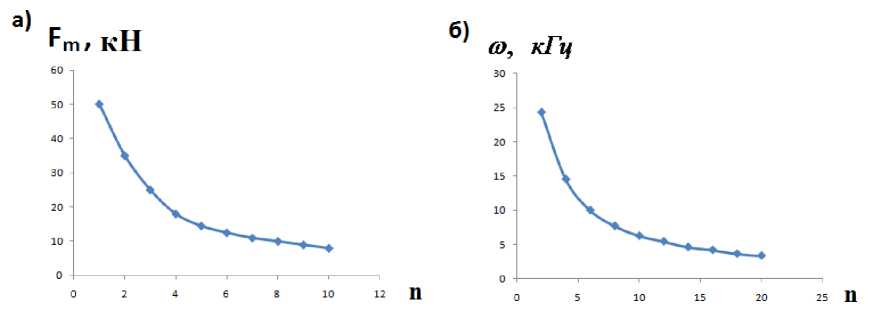
V = i м / c ; ц = o; 5 = 2o • io ^{- 4} мм

Рис. 4. Зависимости максимальных усилий, передаваемых на корпус насоса (а) и их частоты (б) от коэффициента n

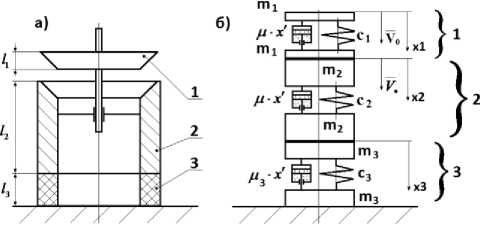
1 – тарель; 2 – седло; 3 – эластичный элемент

Рис. 5. Моделирование удара тарели бурового клапана о седло с использованием эластичного элемента между седлом и корпусом бурового насоса

Так же как в предыдущем случае моделируем та-рель эквивалентным стержнем массой m , который рассматриваем как две массы m = 0.105 кг (величина получена выше), связанные невесомой пружиной, коэффициент     жесткости     которой     равен

С = 2 •Ю10 H /м (также получен выше). Седло, выполненное, как и тарель из стали, смоделировано как в предыдущем случае двумя массами, соединенными невесомой пружиной (с2 = сх / n; m2 = mx • n). Эластичный элемент рассматриваем так же, как две массы m , соединенные невесомой пружиной жесткостью c (рис. 5, б).

Запишем величину коэффициента жесткости С 3 через коэффициент жесткости С . Учитывая формулу (2), можно записать: c_x / c₃ = Е_х • S • / ₃ /( l_x • E ₃ • S ) , или c ₃ = С ; /(( l₃ / l_x ) • ( E / E₃ )) , где l₃ - длина эластичного элемента (рис. 5, а ); E - модуль упругости Юнга для материала эластичного элемента; n 2 = l ₃ / l_x - коэффициент, показывающий во сколько раз длина эластичного элемента больше длины тарели. Окончательно запишем:     С ₃ = С_х /( n 2 • ( E_x IE₃ ))    (5)

Аналогично запишем величину массы m через массу m 1 . Учитывая формулу (3), имеем: m_x / m₃ = S • l_x • p • 3/(3 • S • l ₃ • p ) , где p - плотность материала эластичного элемента. Тогда: m = m , / [ ( l 1 / 1 3 ) • ( p 1 / Р з ) ] = m 1 • n 2 • р з / P 1 (6)

Движение системы с тремя степенями свободы, изображенной на рисунке 5, б , описывается системой трех дифференциальных уравнений:

mx • x‘ = - cx • (xx - x2) - p • (x‘ - x '2)

( n • m 1 + m 1 ) • x 2 = - ( c_x / n ) • ( x ₂ - x ₃) + c_x • ( x 1 - x ₂) - p • ( x 2 - x 3 ) + p- ( x ‘ - x 2 )

(n2 • mx /(p / p) + n • mx) • x‘ = -(cx /(n2 • (Ex / E3))) • x3 + (cx / n) • (x2 - x3) - p • x‘ + p • (x‘ - x‘), где p - коэффициент сопротивления для материала эластичного элемента (p >> p, рис. 5, б).

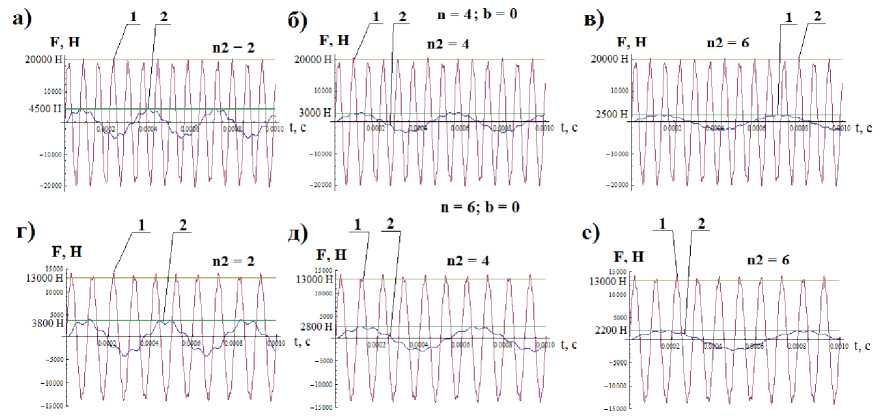
1 – без изолирующего элемента; 2 – с изолирующим элементом

Рис. 6. Усилия, передающиеся на корпус насоса в зависимости от времени при различных значениях коэффициентов n2 и n ( p = p ₃ = 0 ; V_o = 1 м / с ).

Рассмотрим, для примера, в качестве материала эластичного материала текстолит. Для этого материала имеем следующие значения модуля упругости Юнга и плотности [8]: E. = 9 - 10⁹ H / м 2 ; p = 1.15 кг / м ³ .

Тогда, E / E3 = 2.1-1011/(9-109) = 23,33; p /p ~ 7.8/1.15 = 6.78.

На рис. 6 представлены зависимости усилий, передающихся на корпус насоса. Зависимости 1 (без изолирующего элемента) получены решением системы дифференциальных уравнений (4); зависимости 2 (с изолирующим элементом) - решением системы дифференциальных уравнений (7). Решение осуществлялось численно, в пакете «Математика 7» ( ц = ц = 0 ). Как видно из рисунка 6, применение эластичного элемента из текстолита между седлом и корпусом насоса привело к уменьшению в несколько раз величин усилий, передаваемых на корпус бурового насоса (зависимости 1 и 2).

Все предыдущие вычисления были проведены без учета внутреннего сопротивления в эластичном элементе, учитываемого в системе дифференциальных уравнений (7) коэффициентом µ . Известно, что сила сопротивления, пропорциональная первой степени скорости, практически не влияет на период собственных колебаний системы, поэтому не очень важно знать истинное значение коэффициента µ ₃ , которое, кстати, очень сложно определить, а важно знать качественные зависимости при ц ^ 0 .

На рис. 7 представлены зависимости координаты х3 (рис. 5, б ) от времени, полученные численным решением системы дифференциальных уравнений (7) в пакете «Математика 7» при ц = 10000 Н • с / м .

Как видно из этого рисунка, при постоянном коэффициенте n (n=6) время затухания Тзат практиче ски не зависит от изменения коэффициента п2 и, наоборот, при постоянном коэффициенте n2 (n2=6)

время затухания Тзат достаточно сильно зависит от величины коэффициента n.

Для определения материала эластичного элемента с точки зрения эффективного уменьшения величин максимальных усилий, передаваемых на корпус бурового насоса, требуется проанализировать решения системы дифференциальных уравнений (7) в зависимости от отношений Ex / Е3 и p / p, где Ex, p - модуль упругости Юнга и плотность для материала таре-ли (стали); E3, p - для материала эластичного элемента. В табл. 1 эти отношения приведены для различных материалов. Значения модуля упругости второго рода Е3 и плотности p для указанных материалов получены из источников [8, 9].

Как видно из табл. 1, диапазон изменения отношений E / E и p / p для рассмотренных материа- лов следующий: Ex / Е3 - от 0.84 до 456.52; p / p -от 0.86 до 26.

На рис. 8 представлены зависимости усилий, передаваемых на корпус насоса при ударной посадке тарели от времени при различных значениях отношений е, / E₃ ( p / p = 10 - фиксированно; µ = 10000 Н ⋅ с / м ). Данные зависимости получены численным решением системы дифференциальных уравнений (7) в пакете «Математика 7».

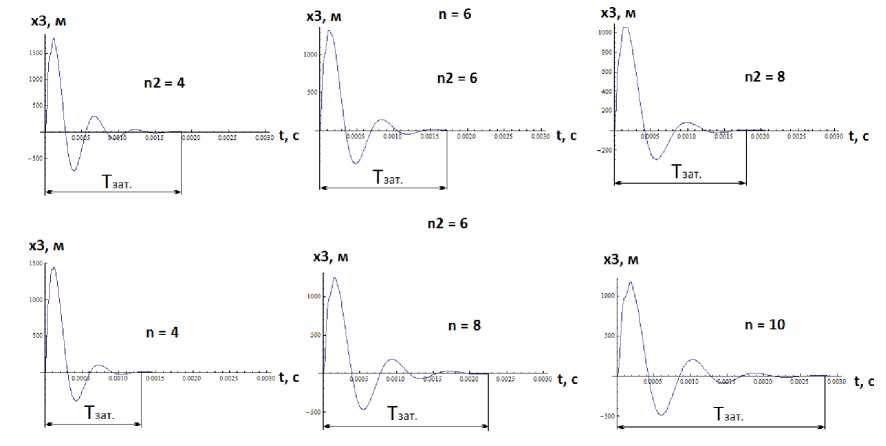
ц = 10000 Н • с / м; m 1 = 0.105 кг ; m ₂ = m 1 • n ; m 3 = n 2 • m_x /( p / p ); V_o = 1 м / c

Рис. 7. Зависимости координаты x3 , характеризующие колебания эластичного элемента от времени при различных коэффициентах п2 и n

Таблица 1

Материал	E 3 , МПа( ⋅ 105)	ρ 3,   кг / м 3 ( ⋅ 103)	E / E	ρ 1 / ρ 3
Медь техническая	1,08-1,3	8,96	1,94 – 1,61	0.88
Чугун: серый модифицированный	0,78 – 1,47 1,2 – 1,6	7,0 – 7,2 7,6 – 7,8	2,69 – 1,43 1,75 – 1,31	1,11 – 1,08 1,03 – 1,0
Бронза: оловянная безоловянная	0,74 – 1,22 1,02 – 1,2	7,5 9,1	2,84 – 1,72 2,06 – 1,75	1,04 0,86
Латунь алюминиевая	0,98 – 1,08	8,2 – 8,8	2,14 – 1,94	0,95 – 0,99
Алюминиевые сплавы	0,69 – 1,71	2,6 – 2,9	3,04 – 1,23	3 – 2,69
Магниевые сплавы	0,40 – 0,44	1,70 – 1,76	5,25 – 4,77	4,59 – 4,43
Никель технический	2,50	8,91	0,84	0,87
Цинк технический	0,78	7,13	2,69	1,09
Гетинакс	0,098 – 0,171	1,2 – 1,4	21,43 – 12,28	6,5 – 5,57
Винипласт листовой	0,039	1,38 – 1,45	53,83	5,65 – 5,38
Органическое стекло	0,028 – 0,043	1,18	75	6,61
Целлулоид	0,0147 – 0,0245	1,400	142,9 – 85,7	5,57
Каучук	0,007	0,9	300	8,67
Стеклопласт	0,34	1,65 – 1,78	6,18	4,73 – 4,38
Фторопласт 4	0,005 – 0,008	2,1 – 2,3	456,5 – 253,0	3,71 – 3,39
Текстолит (ПТ, ПТК, ПТ – 1)	0,059 – 0,098	1,25 – 1,45	35,59 – 21,43	6,24 – 5,38

Как видно из рисунка, при определенном значении отношения E / E ( ≈ 150 ) колебания «пропадают» - начинается апериодическое движение (известное явление).

С увеличением отношения E / E значения максимальных усилий, передаваемых на корпус насоса, уменьшаются. Периоды колебаний T, а, следовательно, и частоты передаваемых усилий ( ω′ = 1 ) определя-T лись визуально по зависимостям типа тех, что показаны на рисунке 8 (решением системы уравнений (7)).

Изменение отношений ρ / ρ практически не влияет на зависимости усилий, передаваемых на кор- пус насоса в отличие от изменения отношений E / E (решением системы уравнений (7)).

Исходя из этого, можно сделать вывод, о том, что при выборе материала эластичного элемента более важно значение его модуля упругости Юнга, чем значение его плотности.

На рисунке 9 представлены зависимости максимальных усилий, передаваемых на корпус насоса (а), и частот этих усилий (б) от отношений E / E .

Напряжения, возникающие в эластичном элементе, определялись по известной формуле: σ = F / S , где S = 20 ⋅ 10 ^{- 4} м ² ; F = 1500 Н (значение получено по зависимости на рисунке 9, а ).

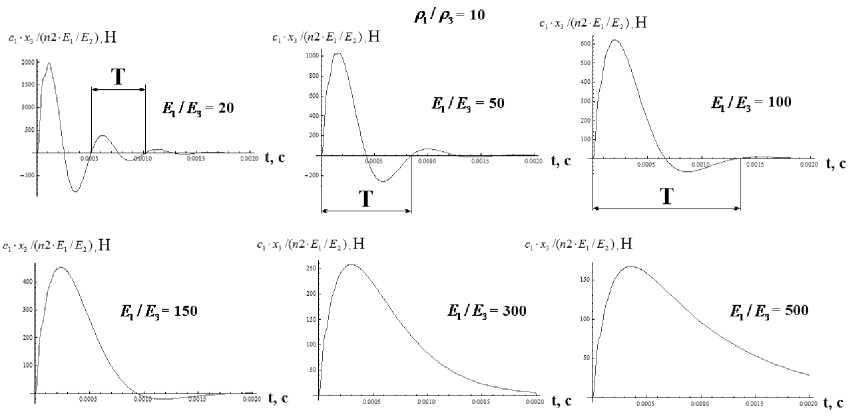
ρ / ρ = 10 ; µ = 10000 Н ⋅ с / м ; V ₀ = 1 м / c

Рис. 8 Зависимости усилий, передаваемых на корпус насоса от времени при различных значениях отношений E / E

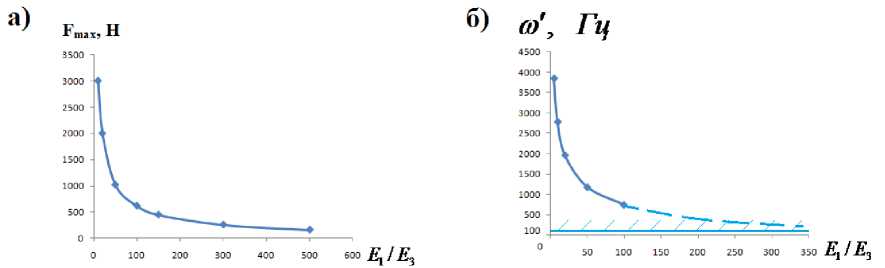
Р / р = 10 ; ^ = 10000 Н ■ с / м ; V_o = 1 м / c ; n2 4

Рис. 9. Зависимости максимальных усилий, передаваемых на корпус насоса ( F^ , а), и частот этих усилий ( to , б) от отноше-

ний E / E

Значение максимального усилия без эластичного элемента взято по зависимости на рисунке 4, а : F^ = 40 кН . Тогда, напряжение в теле седла без эластичного элемента равно:

G = F ^ / 5 = 40000/(2 ■Ю^- 3 ) = 20 МПа ; с эластичным элементом – напряжения в теле эластичного элемента: g = F ^ / 5 = 1500/(2 ■ 10 ^{- 3}) = 0.75 МПа .

В табл. 2 приведены допускаемые напряжения для некоторых материалов, которые можно использовать в качестве эластичного элемента и получившийся коэффициент запаса ^{[ g ]} а , который может достигать двух порядков.

Все предыдущие расчеты были выполнены при условии, что скорость посадки тарели на седло составляет: V = 1 м / c. Анализ решений системы уравнений (7) показывает, что увеличение или уменьшение этой величины приводит к пропорциональному увеличению или уменьшению величин максимальных усилий, передающегося на корпус насоса.

Известно, что для эффективной виброзащиты необходимо, чтобы частота свободных колебаний защищаемой системы с виброизолятором была не менее чем в четыре раза меньше частоты вынуждающей силы, приложенной к системе (с точки зрения не попадания в режим колебаний, близкий к резонансному) [3]. В рассматриваемом случае роль вынуждающей силы играют усилия, возникающие после ударной посадки тарели на седло и передающиеся через эластичный элемент на корпус бурового насоса. Необходимо, чтобы частота этих усилий была минимум в четыре раза больше самой высокой основной частоты собственных колебаний бурового насоса. Как видно из рисунка 10, а самая высокая основная собственная частота насоса составляет примерно 25 Гц, следовательно, частоты усилий передающихся на корпус насоса через эластичный элемент должны быть не менее 100 Гц. Как видно из рисунка 9 б , частоты максимальных усилий, передаваемых на корпус насоса, попадают в «разрешенную» зону (> 100 Гц).

Для изучения динамики и влияния давления на работу клапана проводился спектральный анализ на лабораторном стенде. Измерительная система для ре- гистрации виброперемещения, виброскорости, виброускорения клапанов состояла из датчика давления, цифрового осциллографа, блока питания датчика давления и ПК. Измерения проводились для серийных клапанов и предлагаемых авторами новых клапанов (рис. 2) [10, 11]. Результаты измерений представлены на рис. 10, б, в. Как видно из этого рисунка, для предлагаемого клапана частота вибрации, передаваемая на корпус насоса, при посадке клапанов выше, чем для серийных клапанов. Для предлагаемого клапана частоты замеренной вибрации составляют 450–500 Гц; для серийных клапанов: 100-120 Гц (величины получены визуальным измерением по диаграммам на рис. 10, б, в). Отсюда можно сделать вывод, что для предлагаемых клапанов вероятность возникновения резонанса, вследствие совпадения частот усилий, возникающих при ударной посадке клапанов, с одной из собственных частот бурового насоса намного меньше, чем для предлагаемого клапана (рис. 2).

Таблица 2

Материал	Допускаемые напряжения, [ g ] , МПа		Коэффициент запаса [ g ] / g
	На сжатие	На растяжение
Медь техническая	30–110	30–110	40–147
Чугун	20–160	20–160	26,7–213,3
Бронза	50–110	50–110	66,7–146,6
Латунь алюминиевая	60–130	60–130	80,0–173,3
Алюминиевые сплавы	25–70	25–70	33,3–93,3
Древесина всех пород	10–15	7–13	9,3–20,0
Текстолит	15–30	30-40	20,0–53,3
Резина	> 20	10–20 [42]	13,3–26,6

Кроме того, приведенные замеры вибрации (рис. 10, б , в ) подтверждают вышеприведенные теоретические расчеты. Считая аналогом эластичного элемента (рис. 5, - 3 ) уплотнительное кольцо 3 (рис. 2), можно принять E_y / E₃ = 300 (табл. 1, - каучук). Тогда по зависимости 9, б визуально определяем частоту to ~ 400 — 450 Гц (зависимость получена теоретически). Эта величина практически совпадает с замеренной аппаратурой (рис. 10, в ).

Поскольку частоты вибрации предлагаемого клапана в несколько раз выше частот вибрации серийных клапанов, то перспективным направлением является применение для него эластичного элемента (рис. 5, - 3 ). В этом случае снижение собственной частоты системы седло – эластичный элемент не приведет к резонансным явлениям в корпусе бурового насоса. Работы по применению эластичного элемента для предлагаемого авторами нового клапана (рис. 2) ведутся.

В заключении можно сделать несколько выводов. Для многократного снижения величин максимальных

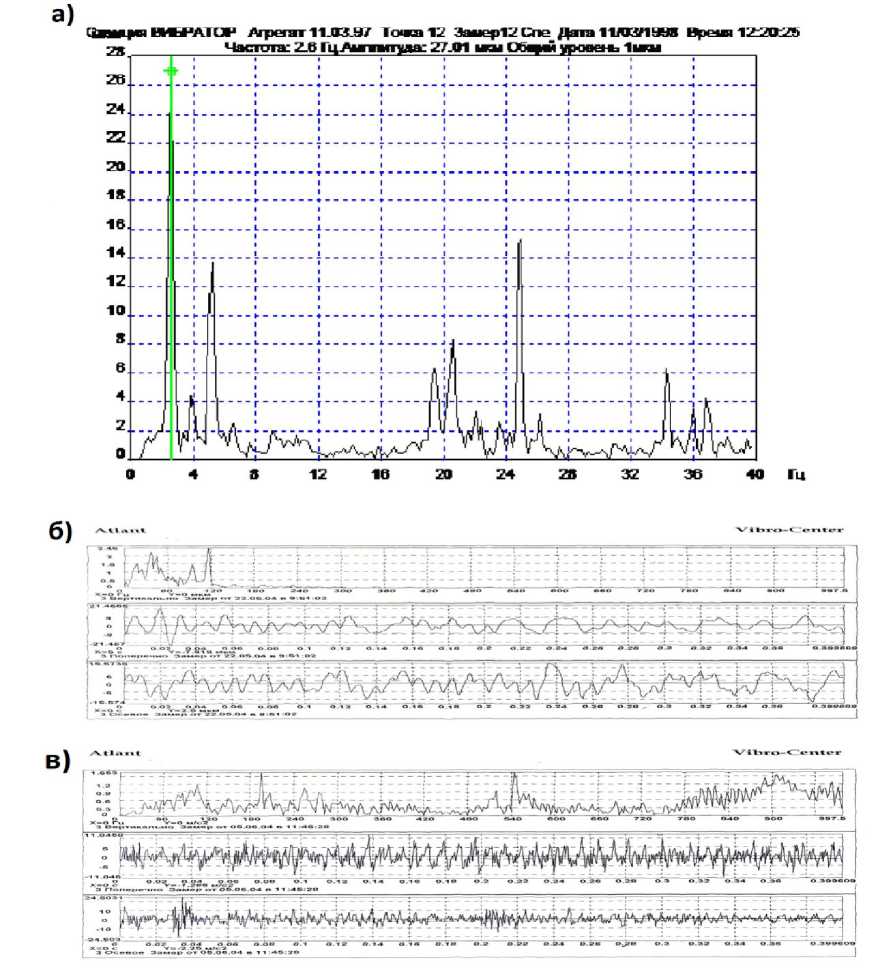
а) спектр основных частот бурового насоса; б) замер вибрации с серийными клапанами; в) замер вибрации с новыми клапанами;

Рис. 10. Замеренные вибрации бурового насоса