Влияние электрического поля на диффузию и распределение частиц в пористых наноструктурированных материалах

Введение. В настоящее время процессам переноса в пористых средах уделяется повышенное внимание. Многочисленные исследования показали, что диффузию в таких средах нельзя описать классическим уравнением диффузии, поскольку появляется аномальная зависимость среднеквадратичного смещения диффундирующих частиц от времени [1]. Она определяет новое автомодельное поведение, а также негауссову форму для устойчивого распределения диффундирующих частиц [2]. Для количественного описания аномальной диффузии в пористых материалах был использован метод обобщенных производных дробного порядка [3-5].

Несмотря на интенсивное исследование проблемы аномальной диффузии тем не менее до сих пор остается ряд нерешенных вопросов. В частности, до конца не исследовано влияние электрического поля на характер диффузионного распространения активных частиц в пористых материалах. Дело в том, что в случае классической диффузии влияние электрического поля можно исключить переходом в инерциальную систему отсчета, движущуюся с постоянной скоростью, - имеется лоренцовская инвариантность; в случае аномальной субдиффузии средняя скорость уменьшается со временем [6-8]:

V(t) ос рЕ / Tt что означает отсутствие лоренцовской инвариантности для субдиффузионных аномальных процессов. Также возникает вопрос о том, каким образом происходит переход к стационарному распределению больцмановского вида в задачах аномальной диффузии.

Статья построена следующим образом. В разделе 2 обсуждается кратко гребешковая модель. В разделе 3 выведено эффективное уравнение диффузии для анизотропной диффузии с учетом влияния электрического поля. В разделе 4 представлен предельный переход к распределению Больцмана. В разделе 5 получены решения интегральных уравнений для функции плотности распределения, а также их графическое распределение. В заключении дано краткое обсуждение полученных результатов.

Модель гребешковой структуры как модель пористых материалов. Напомним коротко гребешковую модель. Впервые она была введена для описания субдиффузии на перколяционных кластерах [9], которая также аналогична перколяции в пористых материалах. Она состоит из хорошо проводящей оси - проводящего канала (аналог скелета перколяционного кластера) и ребер, прикрепленных к оси (рис. 1).

Рис. 1. Гребешковая модель: ось и ребра, прикрепленные к оси структуры

Особенность диффузии в гребешковой структуре состоит в возможности смещения по X _ направлению только вдоль оси структуры (при у = 0). Это означает, что коэффициент диффузии отличен от нуля только при у = 0 [10]:

Те. X - компонента диффузионного тока равна :

6N_ дх

Диффузия вдоль осей структуры носит обычный характер: D = D^.

Следовательно, случайные блуждания на гребешковой структуре описываются тензором диффузии:

₌ (D_X5^ 0

4 I о п2

Используя закон Фика с тензором диффузии (3): j_d=-bw,

получим диффузионное уравнение:

— -D^y^-D, at 1                 2

5² 1

— G(x,y,?) = 8(x)8(y)8(?) 8 у_

Здесь G(x,y,t) - функция Грина уравнения диффузии. Для дальнейшего удобства сделаем преобразование Лапласа по времени и преобразование Фурье по ^— координате:

s+D^ 8(y)-D2 — G(s,k,y) = 8(y)

L                      J                                       (5)

В качестве начальных данных используется точечный источник ^^.х^З^у^З^ , р_ешение уравнения (12) будем искать в виде:

G(s, к, у) = g(s, к) ехр(-Л | у |)

Подставляя решение (6) в уравнение, получим две части: регулярное выражение и выражение с сингулярным коэффициентом ^(г) :

[/ЭД2 + 2X/>2]5O-)^(.v.^.J’) = 5(3Э

Из первого уравнения (7) мы определим значение параметра 4-, а из второго уравнения (8) выражение для функции sG,k):

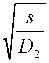
2D2A + Dxk2

Сделав обратное преобразование Фурье, получим выражение для функции Грина:

G(x,y,t) = J(r+ | у |)exp|--

0               \                    4t

Нетрудно проверить, что среднеквадратичное смещение вдоль оси структуры оказывается аномальным:

. (11)

Диффузия вдоль ребер гребешковой структуры носит обычный характер:

=2D,t

Таким образом, анизотропные случайные блуждания в пористых материалах описываются различными степенными зависимостями (11)и(12).

Аномальная диффузия в электрическом поле. Включение электрического поля приводит к анизотропии случайных блужданий. В слабых полях параметр анизотропии мал:

и пропорционален полю. Соответственно, полевой ток имеет вид: J = прЕ .

В гребешковой структуре тензор подвижности равен:

- f А^М 0)

А =

I О

Тогда уравнение диффузии в электрическом поле по гребешковой структуре имеет вид:

р(х,ул) = О

А~г + аАт- -Д2^-А25у — б/           8х"        8.Х J Sv" 8у

Формальное решение уравнения дробного порядка по времени имеет вид: (х-у_хгУ

G(x, у, t,E) = s₀J Je ’° e^ste *^D-^T e ^X^dsd т

Здесь 5₀ = ^—, v_x = ц_хЕ_х, s' = s+s₀.

Предельный переход к распределению Больцмана. Проанализируем полученное выше решение (17), описывающее случайные блуждания по гребешковой структуре в электрическом поле методом перевала. Для этого определим перевальные точки:

• 2 .2            .            ...8

г             х      х

-----— гч--гт-- 4/ 4D2   2D2 ' 4D2r

Выражения для перевальных точек в электрическом поле отличаются от выражений для перевальных точек без поля. Более того сами значения перевальных точек зависят от величины электрического поля.

В пределе слабых электрических полей t <E , где t_E = ^D^J^ время, определяемое компонентой электрического поля, выражение для перевальных точек аналогично формуле без электрических полей:

4/'

Да = —г- •

В случае сильных электрических полей t «t_E перевальные точки описываются выражением

Как следует из выше полученных формул в пределе больших времен, функция распределения принимает больцмановский вид:

N(x.f.EbvoexpL^-^                            <19)

^{Х =}           ( кТ 4Dt J

При этом выход на стационарное распределение происходит медленным диффузионным образом.

Численный анализ функции плотности распределения в электрическом поле. Ниже представлен анализ поведения функции плотности распределения диффундирующих частиц численными методами в системе Matlab и методом Монте-Карло при различных соотношениях параметров задачи: электрическое поле, время и коэффициент диффузии. На рис. 2а-2в представлено поведение двумерной плотности распределения диффундирующих частиц в случае слабых полей.

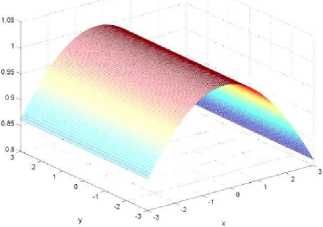
Рис. 2а. В слабых полях поведение значение параметра анизотропии а =0.01

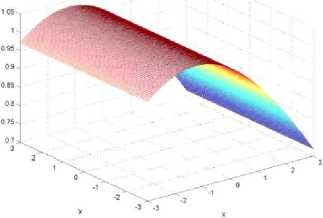
Рис. 26. В слабых полях поведение значение параметра анизотропии а =0.05

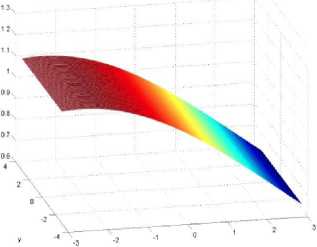
Рис. 2в. В слабых полях поведение значение параметра анизотропии а =0.1

В сильных полях и предельном случае малых времен влияние поля не успевает сказываться согласно развитой выше теории, согласно которой важно соотношение между временем диффузии и «полевым» временем t <E.

В случае сильных полей и обратном предельном случае больших времен, когда время диффузии много больше «полевого » времени t «t_E, влияние поля оказывается существенным. Ниже представлены рисунки для различных значений анизотропии в исследуемом случае:

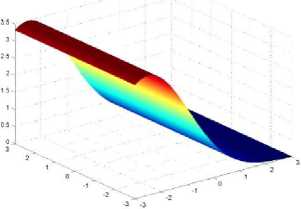
Рис. За. Распределение плотности вероятности в сильных полях и на больших временах: при соотношении времен t / t_E = 1

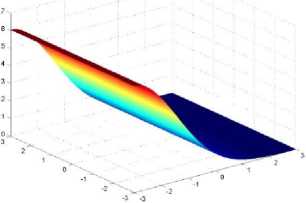
Рис. 36. Распределение плотности вероятности в сильных полях и на больших временах при соотношении времен t / t_E =2

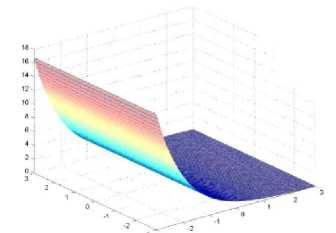
Рис. Зв. Распределение плотности вероятности в сильных полях и на больших временах при соотношении времен t / t_E = 5

Заключение. Исследовано поведение функции плотности вероятности диффундирующих частиц в электрическом поле. Показано, что возможны два предельных случая в зависимости от соотношения времени диффузии t и полевого времени t_E . В случае слабых полей (малых времен) асимптотическое поведение носит аномальный характер аналогично случаю в отсутствии электрического поля. В случае сильных полей происходит сильное изменение формы диффузионного пакета, и на больших временах приобретает характер больцмановского распределения. Выход на больцмановское распределение описывается диффузионной гауссовой асимптотикой.

Полученные результаты будут полезны при исследовании процессов тепло-, массопереноса в пористых средах, которые в настоящее время используются во многих областях. Также в последнее время все более актуальной становится проблема увеличения интенсификации тепло- и массообменных процессов. Различают активные и пассивные методы интенсификации. К пассивным методам относят методы, не требующие дополнительного подвода энергии извне. Активные методы связаны с непосредственным воздействием на процессы физических полей (электрических, магнитных и т.п.). Результаты полученные выше показывают характер распространения частиц в электрических полях в пористых материалах, что необходимо для развития активных методов интенсификации.