Влияние электрического поля на дислокационную неупругость щёлочно-галоидных кристаллов при амплитудах относительной деформации 10 -5–10 -3 в области килогерц

[7] при создании ЭП E ~10⁵–10⁶ В/м наблюдалось поступательное движение дислокаций. При изменении направления вектора напряжённости на противоположное дислокации двигались в обратном направлении. Этот эффект можно объяснить непосредственным воздействием ЭП на заряженные дислокации. Исследование влияния ЭП E =3 ⋅ 10⁵ В/м на кривые напряжение–деформация образцов LiF, NaCl и KCl показало значительное разупрочнение образца в ЭП [8]. Согласно [8], этот эффект обусловлен тем, что под влиянием ЭП облегчается преодоление стопоров движущейся дислокацией. Разупрочнение ЩГК в ЭП с напряжённостью E ~10⁵–10⁶ В/м обнаружено в работе [6]. Согласно [6], ЭП непосредственно действует на заряженные дислокации; вызывает переориентацию комплексов, состоящих из катионных вакансий и ионов двухвалентных примесей, входящих в кристалл по типу замещения; воздействует на заряженные ступеньки на краевой дислокации, вызывая их перераспределение вдоль её длины. Разупрочнение ЩГК при испытаниях в ЭП наблюдалось и в работе [9].

С другой стороны, при работе с электрическими полями E ~10⁷–10⁸ В/м обнаружено не только движение, но и размножение дислокаций [10, 11]. Предварительная обработка ЩГК высокими электрическими полями повышала их пределы текучести [12].

Данные по совместному влиянию ЭП и ультразвука (УЗ) малочисленны. Они касаются в основном влияния ЭП на амплитудную зависимость ВТ ЩГК в области амплитуд относительной деформации ε ₀ 10^-5–10^-4 в ЭП с напряжённостью E ~10⁵ В/м [13–16]. Представляет интерес провести аналогичные исследования в более широкой области амплитуд ε 0 , включающей и размножение дислокаций под действием УЗ, используя электрические поля E ~10⁵–10⁶ В/м. Такие исследования в настоящей работе были выполнены на кристаллах KCl и LiF. Статические пределы текучести кристаллов составляли 0,86 МПа и 11,2 МПа соответственно. Основными двухвалентными примесями, входящими в кристалл по типу замещения, были Ca в KCl и Mg в LiF. Общая концентрация примесей не превышала 10^-6 мольных долей. Исходная плотность дислокаций составляла не более 10⁹ м^-2. Исследования амплитудной зависимости ВТ проводились методом двухкомпонентного резонансного осциллятора в кило-герцевом диапазоне частот [1]. Для создания ЭП на две противоположные грани кристалла наносились серебряные электроды. Использовались образцы с зеркальными сколами, один из которых испытывался в ЭП, другой – в его отсутствие. Образцы протравливались дважды, до и после испытаний. Результаты испытаний в ЭП и без него сравнивались между собой. Наряду с исследованием амплитудных зависимостей ВТ и ДМЮ исследовались также ВАХ образцов.

На рис. 1 представлена амплитудная зависимость образца KCl на частоте 73 кГц в области амплитуд ε 0 10^-7–10^-4 в отсутствие ЭП, т.е. для контрольного образца.

ε 0 , 10^-4

Рис. 1. Амплитудная зависимость внутреннего трения образца KCl на частоте 73 кГц в широкой области

амплитуд ε 0 .

Зависимость δ ( ε ₀) немонотонна, на ней обнаружены два пика. Аналогичные пики в той же области амплитуд ε 0 ранее были обнаружены в KBr [15]и NaCl [16]. Анализ пиков рис. 1 показывает, что они имеют гистерезисную природу и обусловлены отрывом дислокаций от закрепляющих центров. Значения энергии связи закрепляющих центров с дислокацией, рассчитанные по данным работы [17], составили 0,07 эВ для первого и 0,73 эВ для второго пика. Эти данные показывают, что центрами закрепления в области первого пика являются катионные вакансии, в области второго – ионы двухвалентных примесей [3]. Последующее возрастание ВТ δ ( ε ₀) после прохождения второго пика обусловлено процессом размножения дислокаций под действием УЗ. В KCl этот процесс обусловлен работой источников, локализованных в границах блоков, в LiF – гетерогенным размножением от концентраторов напряжений, в основном от краёв образца. После прохождения первого пика внутреннее трение несколько возрастает, достигая определённого значения перед выходом на второй пик (см. участок ab рис. 1). Это значение определяет амплитудно-независимую составляющую ВТ второго пика. Участок ab рис. 1 отвечает выходу заряженного дислокационного сегмента, колеблющегося под действием УЗ, за пределы зарядового облака. Этот факт подтверждается и расчётами по данным ДМЮ величины среднего смещения колеблющегося дислокационного сегмента u [15]. Такой расчёт при амплитуде ε 0 , отвечающей точке максимума первого пика ВТ для KCl, показал, что U = 98 А . Это значение близко к величине радиуса зарядового облака, окружающего дислокацию в KCl [16]. В процессе выхода за пределы облака колебания дислокационного сегмента становятся более свободными, и поэтому ВТ перед началом выхода на второй пик на участке ab рис. 1 несколько возрастает. Амплитудная зависимость ВТ с двумя пиками на кривой δ ( ε ₀) была обнаружена в настоящей работе и в экспериментах с LiF.

Влияние ЭП в области амплитуд ε 0 , отвечающих первому, «малому» пику на кривой δ ( ε 0 ), для разных

ЩГК рассмотрено в работе [16]. Показано, что основная роль ЭП состоит в его непосредственном воздей-

ствии на заряженные дислокационные сегменты, колеблющиеся внутри окружающих их зарядовых облаков. За счёт ЭП дислокации отрываются от катионных вакансий без изменения силы связи их с дислокациями.

В настоящей работе рассматривается влияние ЭП на дислокационную неупругость кристаллов KCl и LiF в области амплитуд ε ₀, отвечающих выходу заряженных дислокаций за пределы зарядовых облаков, отрыву их от ионов двухвалентных примесей и размножению под действием УЗ.

Влияние ЭП на амплитудную зависимость ВТ δ ( ε 0 ) при амплитудах, отвечающих выходу дислокаций за пределы зарядовых облаков в LiF на частоте 40 кГц, представлено на рис. 2.

δ, 10-4

0              1              2              3             4             5         ε₀, 10^-5

Рис. 2. Зависимость внутреннего трения от амплитуды относительной деформации в области амплитуд, соответствующих выходу дислокаций за пределы зарядовых облаков при E =0  (кривая 1) и

E =9,7⋅10⁵ В/м (кривая 2). LiF, f р =40 кГц.

Из рис. 2 видно, что значения ВТ, отвечающие начальным точкам кривых 1 и 2, близки по величине. При последующем возрастании амплитуды ε 0 ВТ образца, испытываемого в ЭП, оказывается выше, чем при E =0. Это можно объяснить тем, что ЭП, непосредственно действуя на заряженный дислокационный сегмент, оттягивает его, переводя в новое положение равновесия. Относительно этого положения и происходят его колебания под действием УЗ. Частью своей длины сегмент выходит за пределы облака. Колебания становятся более свободными, и ВТ поэтому возрастает. При достижении амплитуд, отвечающих конечным точкам кривых 1 и 2 рис. 2, дислокационные сегменты как в ЭП, так и без него, выходят за пределы облаков. Значения ВТ при этих амплитудах в ЭП и без него близки по величине. При отключении ЭП восстанавливается прежнее положение равновесия, относительно которого колеблется сегмент. Зарядовое облако, релаксируя, окружает его. Колебания сегмента снова становятся симметричными относительно облака, и ВТ принимает прежние значения, отвечающие испытаниям в отсутствие ЭП. По данным работы [17], роль за-

рядового облака проявляется при амплитудах ε0, когда ещё не происходит отрыв дислокаций от ионов двухвалентных примесей. Этот вывод согласуется с дан- ными наших экспериментов.

Эффект влияния ЭП в области амплитуд ε ₀, отвечающих второму, «большому» пику ВТ, демонстрирует рис. 3.

³⁰ δ , 10^-5

сложных агрегатов с катионными вакансиями [6]. Переориентация таких стопоров под влиянием ЭП приводила бы к изменению энергии связи их с дислокацией. Этот вывод подтверждается и тем фактом, что в отличие от испытаний в магнитном поле [19], значения амплитудно-независимого затухания для пиков рис. 3 при испытаниях в ЭП и без него практически одинако- вы.

Разупрочняющая роль ЭП подтверждается и дан- ными вольтамперных характеристик [1]. На рис. 4

представлены ВАХ образцов LiF на частоте 40 кГц при E =0 (кривая 1), E =6,5 ⋅ 10⁵ В/м (кривая 2) и E =1 ⋅ 10⁶ В/м

(кривая 3).

_2,5    V р , В

^ -°

0       0,5       1        1,5       2       2,5       3       3,5       4    ε₀, 10^-4

Рис. 3. Амплитудные зависимости внутреннего трения LiF на частоте 60 кГц при E =0 (кривая 1), E =8,7⋅10⁵ В/м (кривая 2) и E =1,1⋅10⁶ В/м (кривая 3).

Из рис. 3 видно, что при испытаниях в ЭП высота пика ВТ возрастает, а амплитуда, отвечающая точке максимума кривой, смещается в область меньших значений. Анализ пиков указывает на их гистерезисную природу. Результаты расчёта параметров дислокационной структуры по методу Супруна – Роджерса [18] по данным для возрастающих участков пиков ВТ рис. 3 представлены в таблице 1.

Таблица 1 Параметры дислокационной структуры LiF по данным рис. 3

Параметр	E =0	E =8,7⋅105 В/м	E =1,1⋅106 В/м
Γ, 10-4	4,4	6,6	7,52
L N , 10-6 м	1,2	1,2	1,1
N 0	17	12	10
F m , 10-10 Н	5,0	4,9	4,89
U , эВ	0,89	0,87	0,86

Здесь Γ – угловой коэффициент возрастающей ветви кривой δ ( ε 0 ) в координатах Гранато – Люкке [18], L N – расстояние между «сильными» точками закрепления, N 0 – число «слабых» центров на отрезке L N , F m и U – максимальная сила связи и энергия связи закрепляющего центра с дислокацией. Значения энергии связи, представленные в таблице 1, отвечают взаимодействию дислокации с ионами двухвалентных примесей [3]. Значения энергии связи U для контрольного образца и при испытаниях электрических полях близки по величине. Этот факт указывает на то, что основной эффект влияния электрических полей, соответствующих кривым 2 и 3 рис. 3, состоит в непосредственном воздействии их на заряженные дислокации без изменения состояния закрепляющих эти дислокации центров. Такими центрами закрепления являются ионы двухвалентных примесей без образования диполей и более

0,5

0            5            10           15           20          V, В

Рис. 4. Вольтамперные характеристики образцов LiF на частоте 40 кГц при при E =0 (кривая 1), E =6,5⋅10⁵ В/м (кривая 2) и E =1⋅10⁶ В/м (кривая 3).

Из рис. 4 видно, что при испытаниях в ЭП образец становится более пластичным, при этом степень пластичности возрастает с увеличением напряжённости E .

Существует пороговое ЭП, вызывающее возрастание ВТ, связанное с отрывом дислокаций от закрепляющих центров. Для примера на рис. 5 (кривая I) представлена зависимость ВТ от напряжённости ЭП образца LiF на частоте 60 кГц при амплитуде относительной деформации ε ₀=1,3 ⋅ 10^-4. Это значение ε ₀ было несколько ниже той амплитуды, при которой в отсутствие ЭП начинала обнаруживаться амплитудная зависимость ВТ (см. рис. 3). Из рис. 5 (кривая I) видно, что при достижении определённой напряжённости E происходит возрастание ВТ, δ ( t ). Это возрастание δ ( t ) при пороговой напряжённости E представлено кривой II рис. 5. После выключения ЭП происходило уменьшение ВТ (кривая III рис. 5). Уменьшение ВТ δ ( t ) происходило в соответствие с законом 5 ( t ) = a — b • t^2/3 , т.е. контролировалось объёмной диффузией. Ионы двухвалентных примесей, диффундируя к дислокации, закрепляли её. Достигаемая после выключения ЭП величина ВТ имела значение, близкое к первоначальному. Это подтверждает ранее сделанные выводы о том, что ЭП не изменяет состояние закрепляющих дислокацию центров.

δ, 10-4

B

0,5

1,5

2,5

C

лами KCl. На рис. 6 представлены амплитудные зависимости ВТ кристаллов KCl на частоте 75 кГц при E =6,7 ⋅ 10⁵ В/м (кривая 1) и E =0 (кривая 2). Амплитуд-

ные зависимости дефекта модуля Юнга

представлены на рис. 7.

³ E , 10⁵ В/м

δ , 10^-4

δ, 10-4

10                              2

ΔΜ

м w

ε 0 , 10^-4

Рис. 6. Амплитудные зависимости внутреннего трения образцов KCl на частоте 75 кГц при E =6,7⋅10⁵ В/м (кривая 1) и E =0 (кривая 2).

0    20    40    60    80   100

t, мин

δ, 10-4

5B

C

III

ε 0 , 10^-4

Рис. 7. Амплитудные зависимости дефекта модуля Юнга

0          10         20          30

ΔΜ

-м (^

образцов KCl на частоте 75 кГц при

E =6,7⋅10⁵ В/м (кривая 1) и E =0 (кривая 2).

t, мин

Рис. 5. Зависимость внутреннего трения от напряжённости электрического поля (см. текст).

Расчёт среднего смещения колеблющегося дислокационного сегмента при амплитудах, отвечающих точкам максимума кривых 1 и 2 рис. 3 ( E =0 и E =8,7 ⋅ 10⁵ В/м) по данным ДМЮ [15] даёт значение 318 А при E =0 и 723 А при испытаниях в ЭП. Радиус зарядового облака, окружающего краевую дислокацию в LiF, составил 103 А [16]. Следовательно, при амплитудах ε ₀ в области пиков ВТ рис. 3 дислокации колеблются за пределами зарядовых облаков. ЭП, непосредственно действуя на заряженную дислокацию, облегчает её отрыв от ионов двухвалентных примесей [16]. Вследствие этого, смещение колеблющейся дислокации при испытаниях в ЭП увеличивается.

Эффекты влияния ЭП на дислокационную неупру-гость были обнаружены и в экспериментах с кристал-

Параметры дислокационной структуры, рассчитанные по данным для возрастающих участков пиков ВТ рис. 6 представлены в таблице 2.

Таблица 2

Параметры дислокационной структуры KCl по данным рис. 6

Параметр	E =0	E =6,7⋅105 В/м
Γ, 10-4	3,10	1,48
L N , 10-6 м	3,90	3,98
N 0	10	4
F m , 10-10 Н	2,72	2,54
U , эВ	0,75	0,70

Из данных таблицы 2 видно, что Fm(0) = 107, т.е. Fm (E)   ’ силы связи стопоров с дислокацией в ЭП и без него практически одинаковы. Этот вывод подтверждается и результатами расчёта отношения Fm(0) по данным

F m ( E )

ДМЮ. Данные ДМЮ позволяют рассчитывать расстояние между «слабыми» точками закрепления на отрезке L_N между узлами дислокационной сетки. В роли «слабых» центров закрепления в области амплитуд ε 0 , отвечающих второму пику ВТ, как уже отмечалось, выступают ионы двухвалентных примесей. Расчёт L c для амплитуд ε ₀, соответствующих точкам максимума кривых рис. 6, даёт значения L c (0)=3,62 ⋅ 10^-7 м и L c ( E) =7,63 - 10 -7 м, так что ^L c ^{( E} ) = 2 ц. С другой сторо-

Lc (0)     ’ ны, угловой коэффициент г  Fm  [18], так что

~ Lc

F m (0) _   Г(0)/Г( E ) . По данным таблицы 1,

F m ( E )   L _с( E)/L_c (0)

П °1 = 2,09, ^{так что} F m ^⁰)- = 0,99.

Г ( E )                F_m ( E )

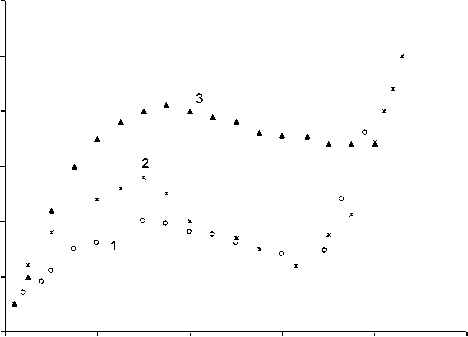
Таким образом, эксперименты с LiF и KCl показывают, что основной эффект влияния ЭП с напряжённостью E~105 В/м в области амплитуд ε0 10-5–10-4, отвечающих отрыву дислокаций от ионов двухвалентных примесей, состоит в его непосредственном действии на заряженные краевые дислокации без изменения силы связи этих ионов с дислокациями. Аналогичный эффект влияния ЭП был обнаружен в опытах с ЩГК при амплитудах относительной деформации ε0 10-7–10-5. В этой области амплитуд в роли «слабых» центров закрепления выступали катионные вакансии, в роли «сильных» – ионы двухвалентных примесей [16]. Как видно из рис. 6, после прохождения пиков ВТ, обусловленных отрывом дислокаций от ионов двухвалентных примесей, ВТ δ(ε0) KCl при последующем увеличении амплитуды ε0 снова возрастает. Аналогичный эффект обнаруживается и в экспериментах с LiF. Это возрастание обусловлено процессами размножения дислокаций под действием ультразвука. Возрастание δ(ε0) может быть обусловлено работой источников, локализованных в границах блоков, или гетерогенным размножением дислокаций от концентраторов напряжений. Размножение от границ блоков начинается при меньших амплитудах ε0, чем от концентраторов напряжений. По способности генерировать дислокации источниками в границах блоков ЩГК можно расположить в ряд: KCl, KBr, NaCl и LiF. В LiF при комнатной температуре источники в границах блоков практически не работали, и дислокации при УЗ воздействии возникали за счёт гетерогенного размножения. Напряжение, отвечающее началу размножения дислокаций при УЗ воздействии, определяет динамический предел текучести кристалла (ДПТ). Его значение зависит от сорта кристалла. Он пропорционален статическому пределу текучести [1]. Как видно из рис. 6, в KCl при испытаниях в ЭП ДПТ оказывается ниже, чем при E=0. Данные повторного травления показывают, что как в ЭП, так и без него, основной процесс размножения дислокаций под действием УЗ контролируется работой источников, локализованных в границах блоков. ЭП стимулирует этот процесс, приводя к уменьшению ДПТ кристалла. В LiF, в отличие от KCl, в отсутствие ЭП источники в границах блоков практически не генерировали дислокаций. При испытаниях в ЭП начальная стадия размножения дислокаций в LiF обеспечивалась уже за счёт работы источников, локализованных в границах блоков. В одном из опытов в процессе измерения амплитудной зависимости ВТ δ(ε0) в отсутствие ЭП была достигнута амплитуда ε0 несколько меньшая той, при которой начиналось возрастание ВТ, связанное с началом размножения дислокаций. Создание в образце при этой амплитуде электрического поля с напряжённостью E=9,5⋅105 В/м вызвало резкий рост ВТ, оно увеличилось в 4,5 раза. При выключении ЭП ВТ уменьшалось со временем, но достигаемое при этом стационарное значение оказалось выше первоначального, до создания ЭП. Повторное травление образца показало развитые полосы скольжения, идущие от границ блоков. Таким образом, при амплитудах относительной деформации ε0 вблизи ДПТ ЭП с напряжённостью E~105 В/м стимулирует работу источников, локализованных в границах блоков. В KCl этот процесс продолжается и при последующем возрастании амплитуды ε0, в то время как в LiF начинает преобладать гетерогенное размножение от концентраторов напряжений. Границы блоков в ЩГК несут электрический заряд. Создание ЭП вызывает перераспределение электрического потенциала вблизи границы блока [8]. Это, в свою очередь, вызывает перераспределение заряженных дефектов внутри границы и увеличивает вероятность образования источников оптимальной длины, способных генерировать дислокации под действием УЗ. При испытаниях в электрических полях с напряжённостью E~106 В/м обнаруживаются новые эффекты, не наблюдаемые в полях с E~105 В/м. На рис. 8 представлены амплитудные зависимости ВТ образца LiF на частоте 40 кГц при испытаниях в отсут- ствие ЭП (кривая 1), E=6,7⋅105 В/м E=1,7⋅106 В/м (кривая 3).

(кривая 2) и

5 ,10^-5

8 0 , 10 - ⁴

Рис. 8. Амплитудные зависимости внутреннего трения образцов LiF на частоте 40 кГц при E =0 (кривая 1), E =6,7⋅10⁵ В/м (кривая 2) и E =1,7⋅10⁶ В/м (кривая 3).

Из рис. 8 видно, что пик, отвечающий испытаниям в ЭП E =1,7 ⋅ 10⁶ В/м (кривая 3), охватывает и ту область амплитуд ε 0 , которая отвечает размножению дислокаций для кривых, полученных при E =6,7 ⋅ 10⁵ В/м (кривая 2) и E =0 (кривая 1). Анализ повторного травления после получения кривых рис. 8 показал размножение дислокаций от концентраторов напряжений (кривая 1), размножение дислокаций от границ блоков (кривая 2), массовое смещение и разрушение участков границ блоков (кривая 3). Размножение дислокаций после получения кривой 3 рис. 8 не было обнаружено. Аналогичный эффект образования «большого» пика, охватывающего область амплитуд, при которых в отсутствие ЭП наблюдалось размножение дислокаций, был обнаружен и в экспериментах с KBr в ЭП E =1,4 ⋅ 10⁶ В/м [19]. По окончании испытаний, так же как и в экспериментах с LiF, обнаруживались изменения в структуре границ блоков. Плотные границы смещались как целое, в рыхлых границах происходило смещение дислокаций в сторону, противоположную направлению вектора напряжённости ЭП. Это показывает, что границы блоков в ЩГК заряжены отрицательно. Размножение дислокаций после прохождения «большого» пика в экспериментах с KBr также обнаружено не было. «Большой» пик на кривой δ ( ε ₀) ранее был обнаружен при испытаниях в магнитных полях (МП) с индукцией B=0,5–0,7 Тл [20]. Однако, в МП, отличие от испытаний в ЭП, наблюдалось резкое возрастание амплитудно-независимого затухания перед началом этого пика. Это указывает на то, что МП, в отличие от ЭП, изменяет состояние закрепляющих дислокацию центров и уменьшает энергию связи их с дислокацией [20].

Проведенные эксперименты показали, что электрическое поле оказывает значительное влияние на амплитудную зависимость внутреннего трения щёлоч-но-галоидных кристаллов. Электрические поля с напряжённостью E ~10⁵ В/м в присутствие ультразвука облегчают отрыв дислокаций от закрепляющих центров и активизируют работу источников, локализованных в границах блоков. В электрических полях с напряжённостью E ~10⁶ В/м при ультразвуковом воздействии происходит смещение и разрушение границ блоков.