Влияние электродинамических сил на характеристики преобразователя ускорений

В автоматических системах управления широко применяются преобразователи второй производной скорости контролируемых по времени объектов в электрический сигнал. При этом в качестве преобразователей могут использоваться емкостные, струнные, индуктивные, индукционные элементы. Однако несмотря на большое количество таких преобразователей, все же возникает потребность в разработке новых преобразователей линейных ускорений в целях расширения их метрологических характеристик.

Решение задачи

Предлагаемая схема преобразователя линейных ускорений (ПЛУ) [1] показана на рис. 1. Данная конструкция обладает улучшенными метрологическими характеристиками, т. е. повышенной чувствительностью и крутизной преобразовательной характеристики за счет дополнительного использования в ПЛУ короткозамкнутого электропроводящего витка.

Улучшение метрологических характеристик ПЛУ достигается усилением изменения магнитного поля в магнитопроводе 1 при вибрации ферромагнитного кольца 2 относительно электропроводящего витка 3, которое далее преобразуется в последовательно-встречно включенных обмотках 4 в информационный электрический сигнал.

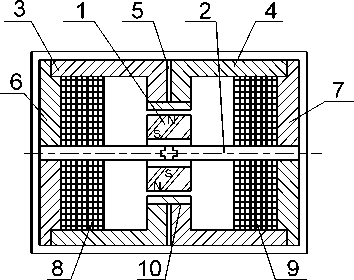
Рис. 1. Конструкция ПЛУ

В данной статье приведено решение задачи по определению преобразовательной характеристики ПЛУ. При решении использованы уравнения динамики, электродинамики Максвелла, методы математического анализа. Расчетная схема ПЛУ представлена на рис. 2.

Задача решена при следующих допущениях; величина немагнитного зазора намного меньше радиуса его кривизны; магнитное поле в зазоре плоскопараллельное; магнитная индукция первичного поля задана основной гармоникой и не меняется вдоль радиуса полюса, магнитная проницаемость материала витка равна проницаемости вакуума μ0, а стали магнитопровода – бесконечности

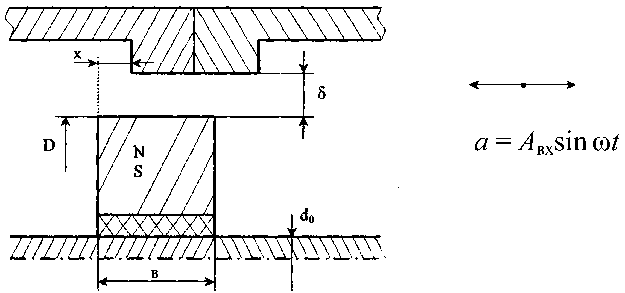
Рис. 2. Расчетная схема ПЛУ

μст =∞; магнитная проницаемость ферромагнитного кольца одинакова и постоянна по всему объему; электропроводность ферромагнитного кольца равна нулю; плотность индуцированных токов по толщине витка постоянна; поля рассеяния вне кругового полюса не учитываются.

Полагается, что информационный сигнал изменяется по гармоническому закону:

a = А _вх sin to t ,                                   (1)

где а – величина информационного сигнала.

Учитывая электромагнитную силу притяжения кольца к явно выраженному полюсу [2, 3], силу тяжести на кольцо в вертикальном положении и силы трения, после математических преобразований уравнение колебательного движения ферромагнитного кольца может быть записано в виде d 2x +   4P    dx + 2B52(D + 25) x _ dt2   рмаг nD2b dt   рмаг H0D2b

2 B. ^!( D + 2 5 )         4 F

= —⁵¹---- - g-g +----- —sin to t ,     (2)

Рмаг H0D        Рмаг H0D b которое после введения постоянных коэффициентов

4p          2 Bs2( D + 25), a =------2“; в _--------2—;

^р маг ^{П D b       р} маг ^H 0 ^{D b}

2 B s ²( D + 2 5 )            4 F 0

C             2    g; K           2    Авх, рмаг H0D            рмаг ПD b

В процессе математического моделирования были рассмотрены следующие частные случаи решения задачи.

1. Электромагнитная сила уравновешивается силой тяжести кольца в вертикальном расположении ПЛУ относительно плоскости колебания контролируемого объекта, т. е.

_ B52 n(D + 25)b_n

Fэм                    рмаг . bg,

2H 0

и уравнение (2) приобретает вид дифференциального уравнения d2x +   4p    dx + 2B52(D + 25) x _ dt2 рмаг П D 2 bdt   рмаг H 0 D 2 b^

4 F

_------0-y sin to t ,                            (6)

^р маг ^{П D b}

решение которого выражается соотношением

А х _-----.                    sin (tot + Ф0 ), to0 ^(1 -X 2) +Y 2 X 2

где λ=ω/ω 0 – относительная частота; γ=2 n ξ/ω 0 – коэффициент учета динамичности колебательной системы (трения и демпфирования короткозамкнутым витком).

При этом ЭДС, наводимая в сигнальных обмотках преобразователя

где A _вх – амплитуда величины ускорения контролируемого объекта; b – ширина полюса; D – диаметр кольца; 5 - величина зазора; р _маг - плотность материала кольца; β – коэффициент динамического трения; F ₀ – внешняя сила возмущения, приобретает вид

^x + А — + Bx _ C + K sin to t ,           (3)

dt2     dt при этом собственная частота для колеблющейся системы

E __{- W}d Ф _ ^{2 n B} 5 ⁽ D ^{+ 2 5)} dt           to ₀

A вх

X

w X

X                               :

^( 1 -X ² ) ² +Y ² X ²

sin ( to t + ф ₀ ) ,

^to 0

2( D + 2 5 )

= ^A      727 ,

V ^р маг ^H 0 ^{D b}

что совпадает с результатами, ранее полученными авторами.

где W – число витков сигнальной обмотки.

Введение базового значения ЭДС

2 п В ₅( D + 2 5 )

ебаз _               Авх w to0

позволяет получить преобразовательную характеристику ПЛУ в относительных единицах

e* _ .       ^          cos ( to t + ф ₀ ) .          (9)

( 1 -X ² ) ² +Y ² X ²

2. Сила тяжести равна нулю Р = mg = 0, когда ПЛУ расположена в горизонтальной плоскости. В этом случае уравнение (2) приобретает вид

d2x +   4p   dx + 2B (D + 25) = dt2 Рмаг nD2b dt   Рмаг Ц0D2b

Анализ этих кривых показывает, что с

_ 2 B ₅ ² ( D + 25 )

^р маг ^Ц 0 D ²

4 F

+-----0-— Sin to t

Р маг ^ D ^b

уменьшением степени успокоения γ возрастает крутизна ПЛУ и при γ → 0 она максимальна, что необходимо учитывать при их проектировании.

На следующем этапе были определены демпфирующие силы короткозамкнутого витка (КЗВ).

Первичное магнитное поле изменяется по

и решение можно найти в виде х = А' + В sin(ω t +φ).

В этом случае для постоянной составляющей справедливо соотношение

2 B5 (D + 2 5) A - —2 B2 (D + 25) ^ A ■ — b, (11)

рмаг Ц0 D 2 b       рмаг Цо D решение исходного уравнения (10) имеет вид

гармоническому закону вдоль оси перемещения магнитного кольца ОХ , следовательно, и электро-

магнитные процессы изменяются также по гармо-

ническому закону

H 1 — Re H 1 ( t ) e j ;

H ₂ — Re H ₂( t ) e - j ^ x ,

x — b +

A вx

^=^= sin (to t + ф₀)   (12)

+ Y2X2

где α=π/2 b ; b – ширина полюса.

При этом уравнение электромагнитного процесса в КЗВ имеет вид

d ² HI,...

——--(a2 + j Цо5to Kd ) H 2 m dy

и выражение для выходного сигнала аналогично выражению (9).

3. Силы трения и демпфирования не учитываются. В этом случае выражение (9) приобретает вид

^

^— j ^Ц 0 ^5to K d^H 3 m ,

* X e — cos (tot + ф ).

1 -X ^{2           0}

При использовании общего выражения колебательного движения ферромагнитного кольца, решение ищется в виде х = А'' + В sin(ω t + φ), посто-

янная составляющая определяется из соотношения

A" — b

1 -

Р маг Ц 0 D ²

B52 (D + 25)_ ’

и выражение для выходного электрического сигнала будет аналогично выражению (9).

На рис. 3 приведена графическая зависимость выходного электрического сигнала ПЛУ от частоты входного воздействия при различных степенях успокоения γ = 2 n ξ/ω₀ в относительных единицах (о.е.).

где δ – электрическая проводимость материала витка; K_d – коэффициент приведения по продольной оси, или

d ² H 2 m dy ²

-X² / 1 2 m

^— j P 0 ^^to K d^H 1 m ,

где  X2 —a2 + j^toKd —«2(1 + 8/.); 8f— ^^Kd f f    d2

магнитное число Рейнольдса (МЧР).

Решение (17) имеет вид

–

■

H _{2 m} — C i sh X У + C ₂ sh X y -

2fa2

72- H 1z m .   (18)

X

С учетом граничных условий для определения постоянных интегрирования С ₁ и С ₂, комплексная амплитуда напряженности вторичного поля КЗВ

H2 m —

-

J4

1 + 82. X f

^- j

1+82

f 7

H 1 m ,

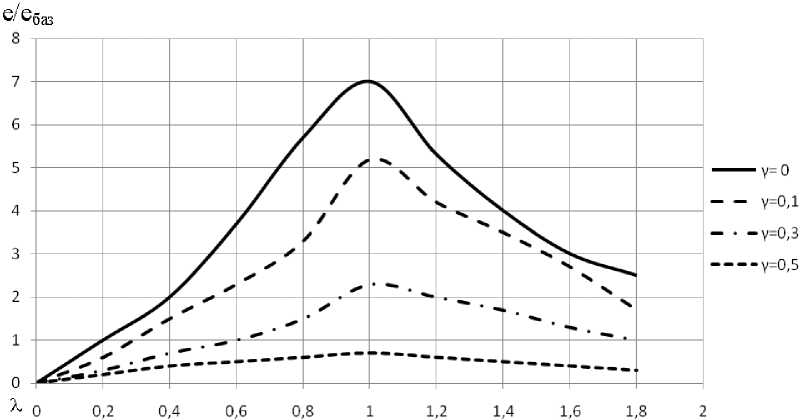
Рис. 3. Зависимость выходного сигнала ПЛУ от частоты входного воздействия

а плотность индуцированного тока в КЗВ

5 H-^ 5 2 = —2m = _a

5 x

8 Г          8 г

+ j f

1 + 8 /     1 + 8 2

к ^{f           f} 7

H 1 m .    (20)

⁴ F        ⁴ B 5    ^{А 1} ср   8

---------------:----:--—

Р маг Ц о Л О 2 b  Р маг Ц о K d bD 2 1 + 8 2

sin to t . (25)

Усредненная по времени сила, действующая на элементарный объём dV , определяется из выра-

жения

B,I,    8f dfxср = -Re(52Bm) = - af,   (21)

^{2             2} Ц о k d 1 + 8 f²

и, следовательно, общая электромагнитная сила, действующая на всё магнитное кольцо

Fx = Ш fxcP dxdydz = xyz

1 B ₁ 2 _m

^{2 Ц} о k d

⁸ f            .

^a—— ² bl cp A , 1 + 8 f ²

где ∆ – толщина КЗВ, l cp – средний периметр КЗВ.

С учетом того, что α=π/2 b , интегральная демпфирующая сила

F ₌ ^ B l m д; x          7   ^'cp

² Ц о k d

⁸ f

1 + 8 f ² ’

что показывает прямую зависимость исходной силы от геометрических соотношений для КЗВ, наличия МЧР, свойства первичного магнитного поля.

Полученное выражение позволяет анализировать динамическую работу КЗВ в ПЛУ с учетом демпфирующей силы для оценки метрологических характеристик, например, определить необходимое изменение значения МЧР, для получения требуемых метрологических характеристик ПЛУ. Следует отметить, что полученная формула соответствует известной формуле Клосса, что свидетельствует о справедливости результатов теоретических исследований и полученных расчетных соотношений [4, 5].

Преобразовательная характеристика ПЛУ с учётом демпфирующей силы КЗВ может быть определена на основании полученных в процессе математического моделирования уравнений механического равновесия для кольца nD2 dd2x           n(D + 25)B5

Р маг —Г"b—f = F 0 sin ® t ⁺     --- "-- b ^—

4     dt ²                   2 ц о

n ( D + 2 5 ) B ₅ ²

^— mg-------

2 Ц о

dx х — p— dt

-

—

n B 5

2 Ц о K d

A 1 ср

8 f

----sin to t .

^{1 +8} f

Полученное уравнение движения ферромагнитного кольца имеет вид d2 x +   4p    dx + 2 B2 (D + 25) = dt2   KD2Рмаг b dt Рмаг Цо KD2b

2 B ₅ ² ( D + 25 ) ---------772-- ^g

Р маг ^Ц 0 ^D

+

После введения постоянных коэффициентов

4 p         2 B ² ( D + 2 5 )      2 B ² ( D + 2 5 )

A =----- ; В =------- v ; С = —g ;

Р маг " ° ^b     Р маг Ц о " ° ^b      Р маг Ц о ^D

⁴ F Q          ^{4 B} 5     ^{A l} ср ⁸ _ л a ⁸

K =--------- Й----Й--T = A BX — A BX ---T

Р маг Ц о Л О 2 Р маг Ц о Kd 5 D ² 1 + 8 2            1 + 8 2

решения уравнения (25) выражается следующими соотношениями f„            A_

X 1 = b +--.                   sin ( to t + ф_о ) ;

^to 0 ^(1 ^— ^ 2 ) ⁺?7 ²

X 2 =

^{4 B} 5    ^{A 1} ср    ⁸ f

РмагЦо Kd bD2 1 + 8 f( x -------.                      Sin (to t + Фо ) = to0 ^(1 — X2 )2 +y2X2

f вх

1 + 8 f to0 ^ (1 — X2 )2 +y2X2

sin ( to t + ф_о ) .

ЭДС, соответствующая каждому из решений (о.е.),

e * = .                  cos ( to t + ф _о ) ;        (27)

( 1—X² ) ² +y ² x ²

*

е 2 =

X

V (1 — X²)² +y ² X ²

cos ( to t + ф _о ) ,

где базовые величины

_pбаз _П ^B ₈( ^D + ^{2 5} ) ^е 1   =

баз e ₂

^{4 B} 5     ^{A 1} ср A

Рмаг ЦоKd bD2 вХ to0

Мгновенный результирующий сигнал по

принципу суперпозиции

* . *

^e 1 ^{+ e} 2

⁸ f

1 + 8 f

X

x                     cos ( to t + ф_о ) ,            (31)

( 1 —X ² ) ² +y ² x ²

действительная величина выходного электриче-

ского сигнала

**

^e = ^e 1 ^{+ e} 2

⁸ f        *     *

------- = ^e 1 ⁺ e 2^K i .

^{1 + 8} f ²

Анализ полученных выражений для различных случаев сигналов МЧР – ε f показывает, что:

1) при 8 f = 0

K i = -^J-_T = 0

⁸ f

8 f и зависимость практически линейная;

• 2)    при 8 f = да

K"      = 0

8'*f и работа ПЛУ неустойчива;

• 3)    при 8 f = 1, с учетом е * = f ( 8 )

K=8 +--

и значение сигнала максимально

• * 1 * *

• е = е +— е = 1,5е .

Таким образом, применение КЗВ позволяет повысить крутизну преобразовательной характеристики и чувствительность ПЛУ в 1,5 раза.

Проведенные экспериментальные исследования зависимости от числа МЧР показали, что при использовании в исследуемом ПЛУ магнитного кольца F =400 А порог чувствительности преобразователя без диамагнитного кольца может достичь значения β=2·10^–4 м/с², а с использованием диамагнитного кольца – β= 4·10^–4 м/с², при этом статическая погрешность коэффициента преобразования при измерениях не превосходит ∆=0,02 % (рис. 4).

Экспериментальные исследования подтвердили результаты математического моделирования ПЛУ, приведенного в данной статье (рис. 5–10).

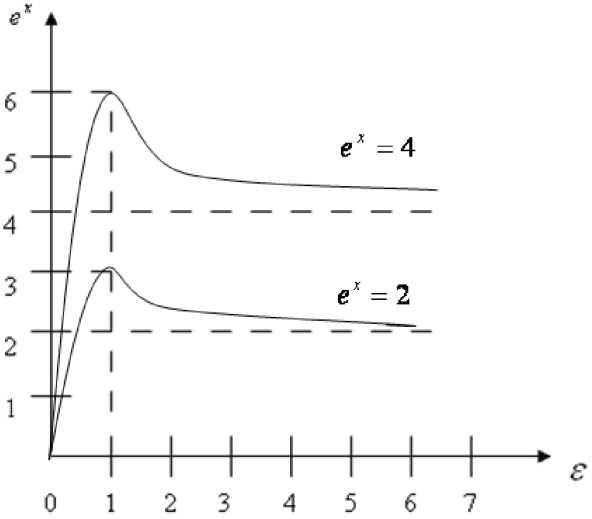
Рис. 4. Выходной сигнал ПЛУ в зависимости от МЧР

Рис. 5. Экспериментальные модели ПЛУ: 1–3 – ПЛУ различного типоразмера

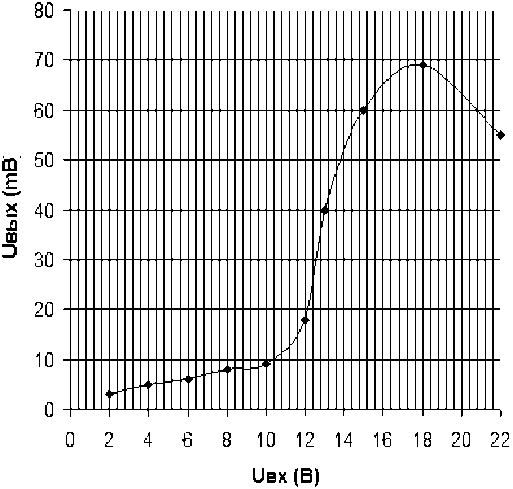
Рис. 6. Выходная характеристика ПЛУ

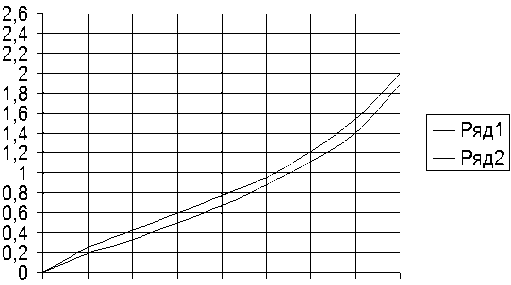
О 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8

Рис. 8. Сравнительная характеристика ПЛУ в относительных единицах: ряд 1 – экспериментальная кривая, ряд 2 – теоретическая кривая

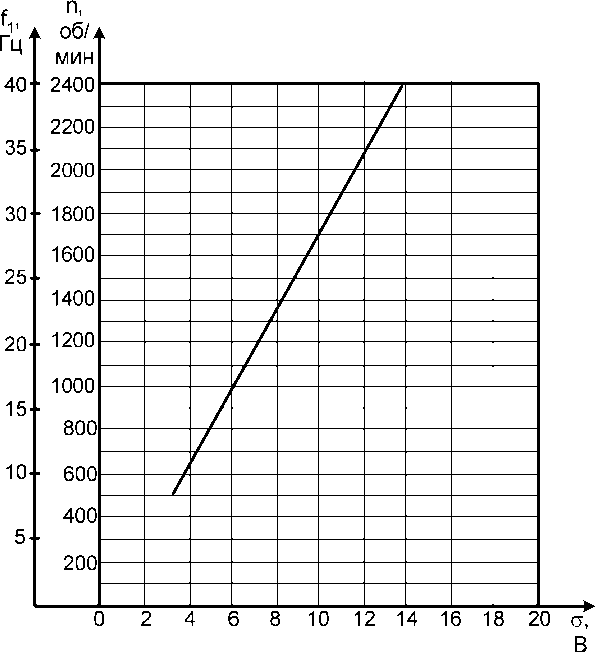
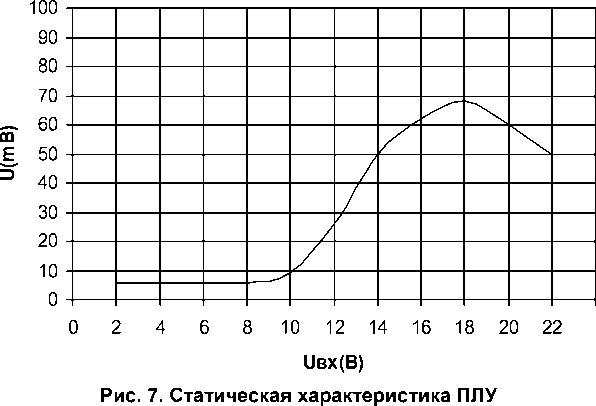
Рис. 9. Тарировочная кривая испытательной платформы: σ – подводимое напряжение к платформе; n – обороты приводного двигателя; f 1 – частота внешнего возмущения

Рис. 10. Испытательный стенд ПЛУ: 1 – испытательная платформа; 2 – универсальный блок питания; 3 – осциллограф; 4 – милливольтметр; 5 – испытуемый ПЛУ

Заключение

Расчетные формулы, полученные в процессе математического моделирования и приведенные в данной статье, дают возможность провести анализ влияния всех параметров ПЛУ как по отдельности, так и в их взаимосвязи на преобразовательные характеристики ПЛУ. Кроме того, указанные формулы обеспечивают возможность конструирования ПЛУ с наибольшей чувствительностью и крутизной преобразовательной характеристики с оптимальным соотношением конструктивных параметров. Выражения, полученные в ходе аналитических исследований, были эмпирически подтверждены проведенными экспериментальными исследованиями. Результаты математического моделирования, приведенного в данной статье, могут найти применения при исследовании электромеханических устройств с наличием КЗВ (индуктивные элементы, электромагнитная пушка, устройства контроля брака об- моток электродвигателей и трансформаторов на замыкание и т. д.).