Влияние электрон-фононного взаимодействия на транспортные свойства в TmxMn1-xS

Введение. Для создания элементной базы микроэлектроники, функционирующей в экстремальных условиях в широкой области температур, например, в малых космических аппаратах и наноспутниках, необходимо использовать новые принципы записи, считывания информации и ее обработки. Полупроводниковая электроника имеет ограничения работы как при низких, так и высоких температурах. Использование спиновых степеней свободы электрона расширяет диапазон температур и допускает возможность создавать наноразмерную элементную базу в микроэлектронике. Принцип записи информации основывается на изменении сопротивления в магнитном поле, так и диэлектрической проницаемости в магнитном поле.

Магнитосопротивление активно исследуется в неоднородных полупроводниках с фазовым расслоением [1; 2], сосуществованием кристаллографических фаз [3–7] и ферронов [8–9]. Кроме заряда и спина, необходимо учитывать орбитальные степени свободы электронов и влияние орбитальных угловых моментов электронов на кинетические свойства в полупроводниках [10– 15] и формирование электронных фазовых переходов [16–19]. В магнитном поле энергия орбитального полярона зависит от фазы электрона [12]. В результате возможен магниторезистивный эффект в отсутствие статических деформаций решетки. Обменное взаимодействие локализованных и делокализованных электронов приводит к аномалиям в температурной зависимости электросопротивления и к образованию магнитосопротивления, которое наиболее сильно проявляется в соединениях с 4f редкоземельными элементами [20–23]. Спин-орбитальное взаимодействие на интерфейсе в полупроводниках приводит к значительному росту величины магнитосопротивления в парамагнитной области. Существует другой механизм магниторезистивных эффектов в области высоких температур до Т = 600 К, если учесть орбитальную степень свободы электрона, то в результате ферромагнитного упорядочение орбиталей электронная структура перестраивается и в магнитном поле индуцируется квазищель на поверхности Ферми [24–25].

Магниторезистивные эффекты зависят от типа носителей тока, решеточных или спиновых поляронов, орбитронов. Для этого необходимо провести исследование структурных характеристик и фононных мод колебаний решетки. Электронное или дырочное допирование в сульфидах марганца приводит к вырождению 3d-орбиталей, которое может сниматься за счет Янн– Теллеровского взаимодействия, либо с образованием орбитального или зарядового упорядочения. Транспортные характеристики зависят от типа магнитной структуры, которая в свою очередь может существенно меняться от взаимодействия спиновой и электронной подсистемы с упругой решеткой [26–35].

Зарядовое упорядочение наблюдается в оксидах переходных металлов и привлекает интерес в связи с эффектом гигантского магнитосопротивления в манганитах в AMnO3(A = Y; P r; Nd:::) [36]. Зарядовая диспропорция является общим свойством для семейства перовскитов AMeO3(A = P r; Nd:::; Me = Mn; Co; Ni) и тесно связана с резким ростом проводимости ниже некоторой критической температуры. В манганитах при нагревании сначала исчезает орбитальное упорядочение и при более высокой температуре исчезает кооперативное упорядочение Ян - Теллеровских искажений октаэдра [37]. В соединениях AMnO3(A = La; P r; Nd:::) образуется щель в спектре одночастичных электронных возбуждений, и сопротивление описывается поля-ронным типом проводимости между этими температурами [37]. Энергия активации находится в интервале 0,3eV < Ea < 1,2eV, и проводимость имеет полупроводниковый тип. Спектральный вес оптической проводимости смещается к низким энергиям при нагревании [38], и в решетке сохраняются локальные искажения октаэдра без изменения угла наклона октаэдра в кластере. Рост сопротивления в манганитах ниже температуры Яна–Теллера объясняется диспропор-цией ионов марганца [37].

Замещение ионов марганца в сульфиде марганца ионами переменной валентности приведет к вырождению электронных состояний, которое может сниматься в результате Янн–Телле-ровского взаимодействия. Что является причиной сильного электрон-фононного взаимодействия и повлияет на резистивные характеристики материала.

Целью работы являеся установить деформации образца и связать их с аномалиями транспортных свойств, которые можно объяснить в модели взаимодействия носителей тока с модами колебаний октаэдра.

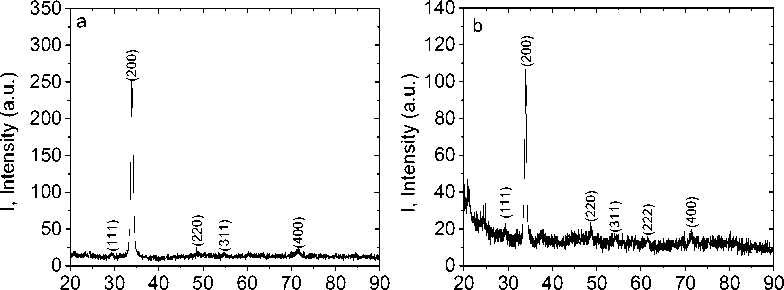
Структура и ИК спектры. Твердые растворы Tm_xMn_1-xS получены методом плавления и кристаллизации из расплава поликристаллического сульфида марганца и поликристаллического моносульфида тулия [39–40]. Рентгеноструктурный анализ сульфидов Tm x Mn 1-x S (0,0 ≤ Х ≤ 0,15) проводился на установке DRON-3 в CuKα-излучении при температуре 300 K после их получения и измерений транспортных свойств. Рентгенограммы соответствуют ГЦК решетке типа NaCl (рис. 1). Рост фона рентгенограммы связан с некогерентным рассеянием на локальных деформациях решетки. С увеличением степени катионного замещения (Х) параметр элементарной ячейки а линейно возрастает от а = 0,55 до 0,64 нм.

2 0, degree                                 2 ©, degree

Рис. 1. Рентгеновская дифрактограмма образцов Tm 0,1 Mn 0,9 S ( a ) и Tm 0,15 Mn 0,85 S ( b ) при комнатной температуре

Fig. 1. X-ray diffraction pattern of the Tm 0.1 Mn 0.9 S ( a ) and Tm 0.15 Mn 0.85 S ( b ) samples at room temperature

Влияние замещения ионов тулия, имеющих больший ионный радиус по сравнению с ионами марганца, на структурные характеристики, в частности изменение объема, по температуре определим из коэффициента теплового расширения, температурные зависимости которого представлены на рис. 2. Относительное изменение объема образца от температуры измерено на дилатометре DIL-402C. Для всех составов наблюдаются минимумы в интервале 260–270 К и при высоких температурах 485–495 К величина минимумов растет с ростом концентрации. При этих температурах рост объема образца замедляется. Уменьшение объема образца, по сравнению с асимптотическим продолжением ∆V/V(T), связано с депиннингом решеточных поляронов выше температуры Дебая TD = 250 K. Небольшие минимумы в α(Т) в интервале 355–370 К вызваны также деформацией решетки. Деформация решетки при Т = 490 К вызвана электронной сжимаемостью образца в результате локализации электронов.

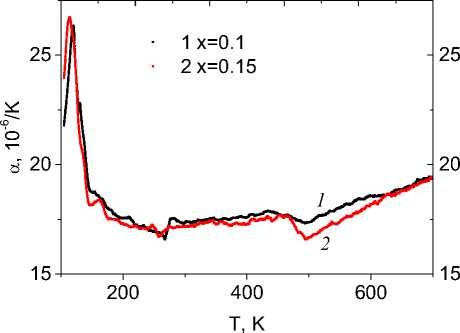
Рис. 2. Температурная зависимость коэффициента термического расширения α(Т) для образцов Tm x Mn 1–x S при x = 0,1 ( 1 ), 0,15 ( 2 )

Fig. 2. The temperature dependence of coefficient of thermal expansion α(Т) for the Tm x Mn 1–x S samples with x = 0,1 ( 1 ), 0,15 ( 2 )

Модель решеточных поляронов подтверждается ИК спектрами, снятыми в интервале частот 450 cm^–1 –7500 cm^–1и температур 80–500 К на Фурье спектрометре ФСМ2202. В этом интервале частот найдено две частоты, интенсивность которых исчезает при нагревании (рис. 3). Для трех составов спектральная линия поглощения в окрестности частоты ω1 = 3116 см^–1 (рис. 4) исчезает в интервале температур 240–270 К. Решеточный полярон ниже температуры Дебая T D = 255 К для сульфида марганца пиннингуется на анионных вакансиях. ИК мода на частоте ω1 = 3116 см^–1 соответствует энергии перехода электрона из локализованного полярона на вакансию.

a

TmMnS x=0.15

80K

122K

142K

162K

181K

221K

240K

260K

340K

380K

1300 ω , cm

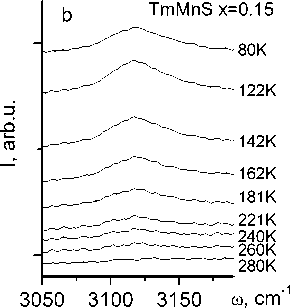
Рис. 3. ИК спектры для образцов Tm_xMn_1–xS при x = 0,15 ( а , b )

Fig. 3. IR spectra for the Tm x Mn 1–x S samples with x = 0.15 ( а , b )

Тепловые колебания ионов, т. е. взаимодействие с акустическими фононами, приводят к депиннингу поляронов, и интенсивность убывает пропорционально плотности акустических фононах I ab ~ 1-AТ. Эта функция качественно описывает экспериментальные результаты с критической температурой отрыва поляронов от дефектов решетки. Интенсивность поглощения на частоте 1240–1320 cm^–1 связана с пиннингованием оптических поляронов на интерфейсе Mn-Tm.

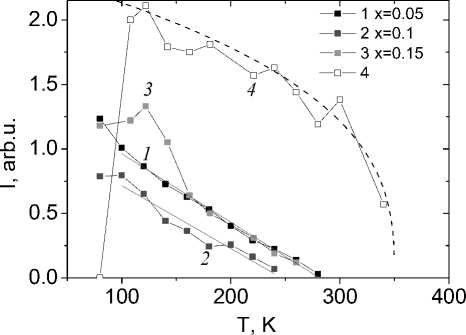
Рис. 4. Температурная зависимость интенсивности ИК спектров для образцов Tm x Mn 1–x S при x = 0,05 ( 1 ), 0,1 ( 2 ), 0,15 ω = 3110 cm^–1 ( 3 ), 0,15 ω = 1290 cm^–1 ( 4 ). Степенная функция I = A(1–T/T_c)^0,35 (пунктирная линия)

Fig. 4. The temperature dependence of the IR spectra intensity for the Tm_xMn_1–xS samples with x = 0.05 ( 1 ), 0.1 ( 2 ), 0.15 ω = 3110 cm^–1 ( 3 ), 0.15 ω = 1290 cm^–1 ( 4 ). The power function I = A(1–T/T c )^0.35 (dotted line)

Деформация октаэдров на границе кластеров Mn-Tm описывается степенной зависимостью I = A(1 – T/T c )^0,35 c температурой Т с = 350 К. При приближении к температуре Т = 500 К найдено увеличение интенсивности поглощения на границе интервала частот 450 см^–1.

В окрестности температур решеточных деформаций и пиннингования решеточных поляронов температурный коэффициент электросопротивления 1/R dR/dT имеет аномалии. На рис. 5 изображены температурные зависимости сопротивления в интервале 100–600 К.

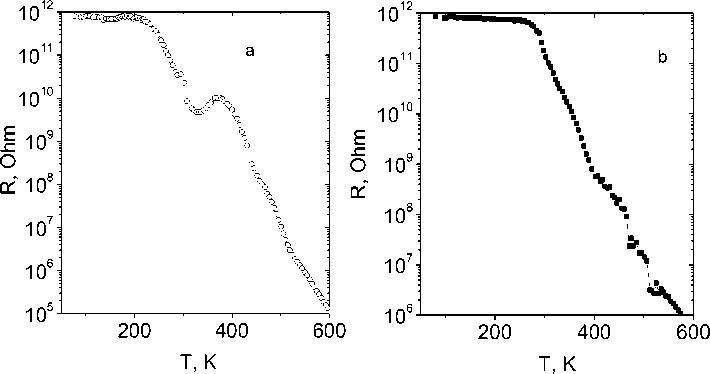
Рис. 5. Зависимость сопротивления от температуры образцов Tm_xMn_1–xS при x = 0,1 ( a ), 0,15 ( b )

Fig. 5. Resistance of the Tm x Mn 1–x S samples with x = 0,1 ( a ), 0,15 ( b ) versus temperature

Для всех трех составов характерно увеличение энергии активации примерно в два раза в интервале температур 340–370 К от ΔE = 0,3 – 0,4 eV до ΔE = 0,6 – 0,8 eV. В этом интервале температур меняется знак коэффициента Холла (рис. 6) и соответственно тип носителей тока с отрицательного на положительный при нагревании. Смена знака носителей тока также наблюдается ниже температуры перехода в магнитоупорядоченное состояние. Рост энергии активации связан со сдвигом химпотенциала от донорного уровня к акцепторному. Несовпадение наков термоЭДС и холловского сопротивления вызвано увлечением электронов акустическими фононами, что обуславливает положительный знак термоэдс ниже Т = 350 К. Аналогичное явление наблюдалось в оксидах [41].

Температура максимума подвижности носителей тока соответствует минимуму электросопротивления. Модель, качественно объясняющая аномалии в электросопротивлении и деформации, рассматривается ниже.

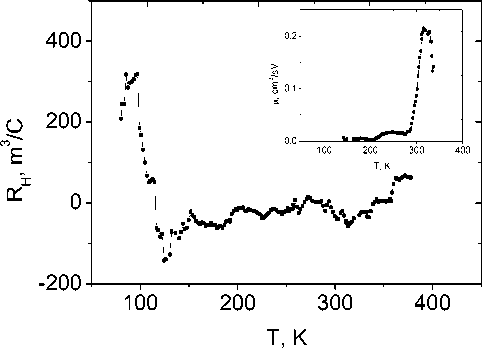
Рис. 6. Температурная зависимость коэффициента Холла, измеренного в магнитном поле H = 8 kOe перпендикулярно току, образцов Tm_xMn_1–xS при x = 0,1. Вставка: температурная зависимость подвижности электронов (носителей заряда) в магнитном поле H = 8 kOe для образцов Tm x Mn 1–x S при x = 0,1 в температурном диапазоне 80–400 K

Fig. 6. The temperature dependence of the Hall coefficient measured in the magnetic field H=8 kOe perpendicular to the current for the Tm x Mn 1-x S samples with x=0.1. Insert: temperature dependence of the mobility of electrons (charge carriers) in the magnetic field H=8 kOe for the Tm_xMn_1-xS samples with x = 0,1 in the temperature range 80–400 K

Модель. Рассмотрим перенос заряда за счет одноэлектронного перескока по узлам анионной решетке в предположении, что уровень Ферми лежит между связывающими и антисвязывающими орбиталями. Вклад в термоэдс дают как одночастичные электронные возбуждения, так и двухчастичные электрон+дырка, имитирующие перемещение ковалентной связи, которую можно описать двухэлектронными возбуждениями по кристаллической решетке и символически представить в виде М ^+3–δ – S^–2+δ – – М ⁺³ → М ^+3–δ – – S^–2+δ – М ^+3–δ. Эффективный гамильтониан переноса заряда имеет следующий вид:

H = H 0 + H 1 + H 2 ,

H 0 = E ( ⁶ d -^ ) c i c i ⁺ E ( ^- ^e 0 ) a a , i a a , i ^— E t 1, j ( a t i a 2, j ⁺ a li a 2 , j ) - i                                 a , i                                     i , j

• ^— E t 2, ik ( c i a a , i^a + k c k ⁺ c ia ^ a P , k c + ) ⁱ E ^A i ( a lt i a 1,i — ai i a 2i i ) ⁺ E Un a 1,i n a 2, j , i , k , a , p                                                                     i , a , p                                             a , i , j

  
  

H = E ^1/O(ai/C + ia+ C )(^+a i ba )iglka\a1kC + ia +k Ck HP+a iPa 1             i, iq    i, it       i, iii q q       2, kq    2, k  k      2, k  k q q i,k,q

H 2 = E ( ® 1 q b q b q ^iro 2 qP^ P q )• ^q

Здесь sd,0 - электронный уровень в атомах 3d металла и ионов серы; ti - интеграл перескока электрона по орбиталям px, py, третий член описывает перемещение ковалентной связи

V ₂, ( а , в = x , У , z )

p р ,3а    ^х                  '

в простой кубической решетке и суммирование проводится по связям

Me - S, c+, a - операторы рождения и уничтожения электронов соответственно на ионах металла и серы, А - параметр кристаллического расщепления орбитального триплета на ионе серы, gi и g2 - параметры взаимодействия электронной плотности на связи Me - S с изгибными и1 и растягивающими и2 модами октаэдра. Составим систему уравнений для электронов и дырок с учетом сохранения операторов второго порядка. Соответствующие уравнения, полученные в приближении случайных фаз, имеют вид dal, i = -(S0 -Ц-А + Una 2 ) al, , -У tu, ,+ha 2, ,+h + У gi, iqCi( bq + b- q ), dt                                                  hi da2,i = -(S0 - Ц - A + Unai )a2,i + У tii,i+hai,i+h + У g2,iqci (p+ + p_q ), dt                                                   hi

^i = - (S d - ^) ci + У gi, iqci ( Ц + Ь- q ) + У g 2, iqci ( p+ + p - q )’ dt                                i, qi

^( ^a i, i b - q ) = ^- ( ^S 0 ^- Ц ^{- A} + Un a 2 - ® i, - q n - q )( ^a i, i^b - q ) - g i, iq ( ⁱ ■ n - q ^- n a i ) c i ,

(ai,ibq ) = - (S0 - ^ - A + Una2 dt

⁺ ® i q n q ) ( ^a i, i b q ) + g i, iq ( n q + n a i ) c i ,

^ ( ^a 2, i p - q ) = ^- ( ^S 0 - ^Ц - ^{A +} Un a i - ® 2, - q n - q )( ^a 2,^ - q ) ^- g 2, iq ( ^{i +} n - q ^- n a 2 ) ^Ci ,

d

^^{( a} 2^, i p q ⁾ = ^-(S 0

- Ц - A + Unai + m,qnq )(a2iiP+q ) + g2,iq (np + na2 )ci, iddt (cibq)=(S d- ц+mi, qnq)(cibq)- gi, iq (nq+nc) ai, i ’ ddt (cipq ) = (Sd - Ц + m2,qnp )(cipq ) - g2,iq (np + nc ) a2,i, iqdt (cib- q)=(S d- ц+mi,-qn - q)(cib- q)- gi, iq (i+n - q- nc) ai, i, id ( cip - q ) = (S d - Ц + m2,-qn - q )( cip - q ) - g 2, iq (i + n - p - nc ) a 2, i,

где n-q, nq, n-p, np средние числа заполнения фононов вследствие симметрии оптических фо нонных мод относительно центра зоны  n-q = nq, n-p = np   и определяются как nq p =( exp (h mi2/ kT -1)) . Параметры заполнения зон nc, nai2 определяют положение химпо- тенциала.

Гриновские функции для дырок G^ =\ ^ ^а a k| a а к)/ ^и поляронов G^q q =/( c _k b | +_+q | a a _k

+

G k p - q q

^c k ^c к p к - q| ^a a , k))

имеют следующий вид:

( «+ a „) .   .8 ( k ) G ” - g kq ( G?^ + G k b q ) = 0,

^-8 1 ^{( k} ) G . ^e + ( o+ a pp ) . р ^{- g} p kq ( G b q ⁰ + G k — q ) = 1, g a kq ⁽ n q ⁺ n k ) ^G k ^{+ G} k + q ^{(to + 8} d ⁺ Ц ⁺ n q ^to a , q ) = ⁰, g a kq ( 1 ⁺ n q ^- n k ) ^GV^{? +} G k b -q ( ^{to + 8} d ⁺ Ц ^- n q ^to a , q ) = ⁰, g P kq ( n p ⁺ n k ) ^G k ^{P +} G ^ ( ^{to + 8} d ⁺ Ц ⁺ n p to p , q ) = °, g P kq ( 1 ⁺ n p ^- n k ) ^G k ^{P + G} k p q ( ^{to + 8} d ⁺ Ц ^- n p ^to p , q ) = ⁰, £ 1 ( k ) = - 2 1 1 ( cos ( k x / 2 ) • cos ( k y /2 ) + +x ( cos ( k z / 2 ) • cos ( k x /2 ) + cos ( k z /2 ) • cos ( k y /2 ) ) ) ,

где параметр λ описывает анизотропию интегралов перескока в плоскости и между плоскостями, ниже использовалось значение λ = 0,25. Гриновские функции электронов для дырок Gk“=( (kk |kk)) и поляронов Ga+q = { aa a,k bk . q kkJ к G-q =( (a a,k Fk-q| kkt к образуют слеДУю— щую систему уравнений:

^{(to + 8} d ⁺ Ц ) ^G k ^{k + g} 1 kq ( G k + q ^{+ G} k - q ) ^{+ g} 2kq ( ^G k + q ⁺ G k к ) = 1,

-g 1kq ( nq + na 1 ) Gk +(to+80 -Ц-A- Una 2 + nq toiq ) Gk+q = 0, g 1kq (1 + nq + na 1 ) Gk + (to + 80 - Ц - A - Una2 - nqto1q ) Gk-q = °,                (4)

-g2kq (np + na2 ) Gk + (to + 80 - Ц + A - Una 1 + npto2q ) Gkpq = 0, g 2kq (1 + np + na 2 ) Gk^ +(to+80 -Ц-А-Una 1 - np to2q ) Gk-pq = 0.

Флуктуации связей Me – 0 описываются двумя операторами рождения дырки на кислороде и уничтожения электрона на ионах металла:

^d -( ^k/^a + i ) = ( ^ki^a + i ) ( n a 1 ( ⁸ 0 ^{- 8} d ^{- A} ) ^- ^ ( n k ⁺ n a 1 ) ^- n a 2 ( U ^{+ 8} d ) ) ^- n a 2 E t 2,i,h 1 ( ^ki + h 1 ^a + i + h 1 ) ^- dt                                                                                    _{h 1}

-na2 E t2,i,h 1 ( a2,i+h 1 ki+h 1) + na 2 E g 1,iq (Ь+ + Ь-q ), h1                                     q d ( + . iac dt  2,kk

( ^a + k^kk ) ( n a 1 ( ⁸ 0 ^{- 8} d ^{- A} ) ^- Ц ( n k ⁺ n a 2 ) ^- n a 1 ( U ^{+ 8} d ) ) ⁺ n a 1 E t 2, i , h 1 ( ^a 2 + , k + h 1 ^kk + h 1 ) ^- h 1

-

'n a 1 E t 2, k , h 1 ( ^kk + h 1 ^a 2 , k + h 1 ) ⁺ n a 1 E g 2, kq ( pq ⁺ p - q ) , h 1                                        q

iddtb q = ^to 1 b q ⁺ E g 1i ( ^a 2, i^k^ ^{+ a} 2 ⁺ , i^ki ) , iddtp q = ^to 2 p q ⁺ E g 2 1 ( ^a 2, l^k + ^{+ a} 2 ⁺ , l^kl ) .

При выводе уравнений использовался закон сохранения заряда М+3–δ – S–2+δ, связанный с переносом электронной плотности с серы на катион металла и пренебрегалось корреляционными эффектами между разными орбиталями. Параметр δ определяет ковалентный вклад на ионе.

Представим оператор двух фермиевских частиц в виде т k = L q c_k + q a^ q и k k = L q a 2 + q c k + q

Введем гриновские функции для одного типа связей G ] =Цт_к |тк\ V G ] ^т =( d k _к| т _к

G k b ^т = \ \ b k | тк / /, G ] ^т = \ \ Р k | тк / /. Система уравнений имеет вид

( to- ^а 1, т ) ^G k ⁺ n a 2 ^S 2 ( k ) ^G _k ^{т +} g 1 к n a 2 G k ¹ = ^G 1 , n a 1 ^S 2 ^{( к} ) ^{G т} + ( ^to - ^a1,k ) ^G _k ^{1 +} g 2 k n a 1 G k ¹ = 0, g 1 k ^G k + ^(to - ^to i ) G b ^т = 0,

- g 2 k ^G k ^{I +(to} - ^to 2 ) ^G k ' - 0,                  ⁽⁶⁾

a1,т = na 1 (SQ — Sk - A)- ^(nc + na 1 ) - na2 (U + Sk ) - na2 ' S2 (k), al,k = na2 (SQ - Sk + A) - ^(nc + na2 ) - na 1 (U + Sk ) + na 1 ' S2 (k),

S 2 ( к ) = - 2 1 2 ( cos ( k x ) + cos ( k y ) + cos ( k z ) ) .

Система уравнений для гриновских функций с другим типом связей G^ = ( (k _к | k _к +

^G к ^k = ((^тк | ^k к⁺ }) , G ^ = ( b b_k |^k к⁺)) , G ^ ¹ = ( p p к | ^k к⁺ ^ имеет вид

( to- a 1, k ) G ^ + n a 1 S 2 ( к ) G ] ^k + g 2 к n a G p = G 2 , n a 2 ^S 2 ^{( k} ) G k + ( ^{to- a} 1, т ) ^G k ^{k + g} 1 k n a 2 ^G k ¹ = 0, ( -to + to 2 ) G p + g 2 k G k = Q, ^(-to + ^to 1 ) ^G k ^т + ^g 1 k ^G k ^k = ^Q.

Химпотенциал вычисляется самосогласованно путем численного решения системы трех уравнений:

n c = -1 LI ^{k to} f ( ^to ) 1Im G i cc q ,

N k,q na 1 =   Lj kto f (to) ^Im Gk1q,

N k,qJ na 2 = 717 LIkto f (to) ^Im GM, N k,q где f (to) = ( exp (to / T) +1) . От суммирования по импульсам можно перейти к интегрированию с учетом затравочной электронной плотности состояний, либо произвести прямое вычисление суммы по электронным и фононным импульсам по первой зоне Бриллюэна c шагом Δk = 0,2 по 109 точкам, что невозможно выполнить на современных компьютерах. Чтобы обойти эту проблему, предположим, что оптические моды и функция связи экситона (электрон+ дырка) с фононами не зависит от импульса q. Это эквивалентно рассмотрению взаимодействия с длинноволновыми оптическими модами колебаний.

ω/ t

ω / t

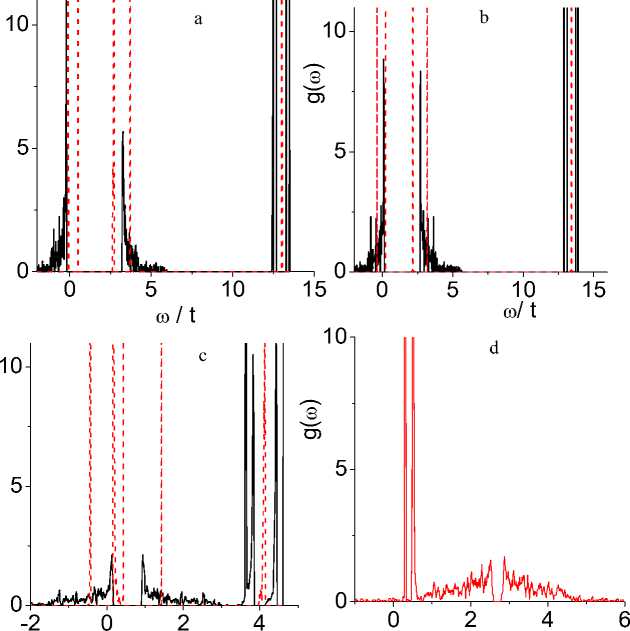
Рис. 7. Плотность состояний для одночастичных электронных возбуждений при следующих параметрах: ( a ) ∆= 1,5, U = 3, ω 1 = 0,25, ω 2 = 0,4, g 1 = 0,02, g 2 = 0,3, n c = 0,2, ε o – ε d = 15 и T = 0,02; ( b ) то же самое и T = 0,6; и ( c ) ∆ = 1,0, g ₁ = 0,6, g ₂ = 0,05, n_c = 0,32, ε _o – ε _d = 5 и T = 0,02. Плотность состояний для двухчастичного возбуждения (электрон+дырка) при ( d ) ∆= 1,5, U = 3, ω 1 = 0,25, ω 2 = 0,4, g 1 = 0,02, g 2 = 0,3, n c = 0,2, ε o – ε d = 15 и T = 0,02

Fig. 7. Density of states for one-particle electron excitations at the following parameters:

• ( a )    ∆= 1.5, U = 3, ω₁ = 0.25, ω₂ = 0.4, g ₁ = 0.02, g ₂ = 0.3, n_c = 0.2, ε _o – ε _d = 15, and T = 0.02;

• ( b )    the same and T = 0.6; and ( c ) ∆ = 1.0, g 1 = 0.6, g 2 = 0.05, n c = 0.32, ε o – ε d = 5, and T = 0.02.

The density of states for two-particle (electron + hole) excitations at ( d ) ∆ = 1.5, U = 3, ω 1 = 0.25, ω 2 = 0.4, g 1 = 0.02, g 2 = 0.3, n c = 0.2, ε o – ε d = 15, and T = 0.02

Ромбическая анизотропия в (1) фактически отражает взаимодействие псевдоспиновых орбитальных моментов серы τ ^z = a ₁ ⁺ a ₁ - a ₂ ⁺ a ₂ с кристаллическим полем и приводит к расщеплению зоны на две подзоны, которые начинают расходиться с увеличением параметра ромбической анизотропии. В области щели оказываются две узкие поляронные мини-подзоны, положение которых меняется в зависимости от константы электрон-фононного взаимодействия, одна из которых находится над потолком валентной зоны и образована в результате взаимодействия электронов с изгибной модой колебаний. Другой уровень лежит вблизи дна зоны проводимости и обусловлен взаимодействием электронов с растягивающими модами октаэдра. Локализованные состояния электронов на 3d ионах металла находятся высоко по энергии и на рис. 7 a , b представлены рядом линий в интервале энергий ω/ t = 10 - 15. Типичное поведение плотности состояний для разных параметров электрон-фононного взаимодействия представлено на рис. 7. Для малых параметров g 1 << 1, g 2 << 1 поляронные мини-подзоны стягиваются в узкие линии, подобные примесным состояниям в полупроводниках. Их взаимное расположение относительно химпотенциала определяет температурное поведение сопротивление.

Для фононных частот ω 1 / t = 0,2, ω 2 / t = 0,4 и параметра ромбического искажения, соответствующего Янн–Теллеровским искажениям решетки Δ/ t = 1,3, можно получить разные зависимости температурного поведения сопротивления, определяемые параметрами электрон-фононного взаимодействия и величиной ромбического искажения кристаллического поля. Уменьшение ширины щели с ростом температуры приводит к смещению потолка валентной зоны относительно химпотенциала и при некоторой критической температуре химпотенциал перемещается в зону, что вызывает резкое уменьшение сопротивления.

Заключение. В твердом растворе Tm x Mn 1–x S установлены температуры, при которых объем образца меняется, температурный коэффициент электросопротивления имеет максимум. Найдены температуры исчезновения ИК спектров поглощения на определенных частотах. Деформация решетки обусловлена локализацией электронов в окрестности ионов тулия в результате электрон-решеточного взаимодействия с акустическими и оптическими модами колебаний решетки при понижении температуры. Отрыв электронов индуцирует максимум подвижности носителей тока. Предложена модель взаимодействия электронов и дырок с изгибными ω 1 и растягивающими ω 2 модами октаэдра. В приближении случайных фаз рассчитана электронная структура, спектр электронных возбуждений. Найдены поляронные уровни в плотности состояний, связанные с изгибными и растягивающими модами октаэдра.