Влияние энергий взаимодействия между атомами углерода в ГЦК-железе на концентрационную зависимость активности углерода

Сплавы на основе системы железо – углерод, несмотря на развитие производства пластмасс, керамики, композитов, остаются основными конструкционными материалами. Железо является полиморфным металлом [1, 2]: при нагревании выше 911 °С низкотемпературное α-железо с ОЦК решеткой превращается в γ-железо с ГЦК решеткой. Углерод растворяется в обеих фазах железа, так что при температурах выше 723–911 °С существует аустенит – раствор углерода в γ-Fe, ниже этого интервала возникает феррит – раствор углерода в α-Fe [2].

В условиях быстрого охлаждения аустенита, когда диффузия углерода подавлена, происходит бездиффузионное мартенситное превращение, при котором все атомы углерода переходят в решетку мартенсита, а последняя, хотя и похожа на решетку α-железа, но имеет слабую тетрагональность [1–3]. Возникновение тетрагональности и бездиф-фузионный характер мартенситного ГЦК-ОЦК превращения был объяснен Бейном, который обратил внимание, что ГЦК решетку можно превратить в объемно-центрированный куб при небольшом сжатии вдоль оси ОZ и растяжении в направлениях осей OX и OY (бейновская деформация). Октапоры ГЦК решетки вместе с располагающимися в них атомами углерода переходят только в октапоры типа «Z» решетки ОЦК-железа. При этом все атомы углерода растягивают решетку в одном Z-направлении, и она из кубической превращается в тетрагональную. Хотя теория Бейна общепризнана, вопрос теоретического обоснования ее справедливости остается открытым.

В связи с этим, вопрос о характере взаимодействии между атомами углерода в ГЦК-решетке железа, определяющим их упорядочение, является важнейшим для физического металловедения. К сожалению, энергии взаимодействия атомов растворенного вещества не могут быть непосредственно измерены в эксперименте. Они могут быть оценены, с помощью термодинамических моделей на основе фазовых диаграмм или измерений параметров ближнего порядка [4].

Долгое время наиболее чувствительной к особенностям распределения атомов углерода по октапорам считалась активность углерода в γ-фазе a _С ^γ [5]. Вагнер с сотрудниками [6] показали, что при отсутствии взаимодействия между атомами углерода величина активности дается выражением

a

^γ С =

x _С

1 - β x _С

где xС – доля атомов углерода в сплаве, а коэффициент β = 2. Однако результаты экспериментального изучения активности углерода в γ-железе, показали, что величина aСγ с увеличением содер- жания углерода возрастает сильнее, чем это предписывает формула (2). Было высказано предполо- жение, что это обстоятельство связано с наличием отталкивания между ближайшими атомами углерода, что и приводит к уменьшению числа возможных мест их расположения.

Темкиным и Шварцманом [7], а затем Кауф маном [4] была развита модель блокировки, в кот орой выдвинуто предположение, что каждый атом С блокирует, т. е. делает недоступным для заполн е ния другими атомами углерода, некоторое число m октапор, ближайших к нему. В этом варианте:

In a X = In — x ^c —. (2) С 1 - ( m + 1 ) x_c

Позднее Л.А. Большовым [8] была развита более общая теория, у читывающая энергии вза и модействия пар атомов углерода не только в пе р вой, но и последующих координационных сферах.

Важные данные о распределении углерода были получены на данным экспериментов по ядерному гамма- резонансу (ЯГР) [9 –13]. Обзор существующих дан ных о распределения углерода в аустените был сделан В.Г. Гаврилюком [9] и В.М. Надутовым [10].

Авторы работ [11– 12] сочли, что данная мет о дика недостаточно точна, и приняли решение пр о водить расчёты подгонкой кривых активности под экспериментальные кривые. Энергии взаимоде й ствия подгонялись при помощи метода Монте - Карло под экспериментальную кривую темпер а турной зависимости активности углерода в гамма - железе от концентрации углерода. Получено, что энергии взаимодействия между атомами углерода составляют Е ₁ = 0,036 эВ и Е ₂ = 0,075 эВ [12] и Е 1 = 0,115 эВ и Е 2 = 0,169 эВ [11] ( E 1 и E 2 – энер гии взаимодействия между атомами углерода в ГЦК- железе находящихся в первой и во второй координационных сферах). Из этих данных видно, что используя разные энергии взаимодействия можно получить согласие с экспериментальными данными по активности.

Поскольку все рассмотренные и сильно ра з личающиеся модели позволяют довольно точно описать активность углерода в аустените или да н ных мёссбауэровских спектров, можно заключи ть, одной активности недостаточно, чтобы провести детальную реконструкцию распределения углер ода в ГЦК-железе. Поэтому в последнее годы все большее внимание уделяется методам первопри н- ципного компьютерного моделирования, г лавным достоинством которых являет ся отсутствие каких - либо входных данных, влияющих на достове р ность результатов, при использовании минимал ь ного количества подгоночных параметров. Нами уже были вычислены энергии взаимодействия м ежду атомами углерода в ГЦК- железе в работе [14], но затем они были уточнены в работе [15].

Целью данной работы является проведение первопринципных расчетов энергий взаимодейс т вия между атомами углерода в парамагнитном

γ-Fe, а затем на их основе, используя метод Монте-Карло, получить концентрационную зависимость активности углерода в гамма-железе при различных температурах. По результатам сравнения полученных кривых с данными эксперимента можно оценить достоверность данных первопринципного расчёта [15].

Методика

В данной работе расчёты проводились из первых принципов полнопотенциальным методом LAPW, с учетом обобщенного градиентного приближения PBE-GGA в программном пакете WIEN2k [16]. Это наиболее точный метод используемый в рамках теории функционала плотности. В нашей модели с помощью программы BINAR [17] были получены 16 различных неэквивалентных магнитных конфигураций (рис. 1), из которых были выбраны 5 наиболее низколежащих по энергии. Потом с помощью усреднения по статистическому ансамблю вычислялись энергетические параметры. Более подробно параметры, методика и модель парамагнитного состояния обсуждены в нашей предыдущей работе [18].

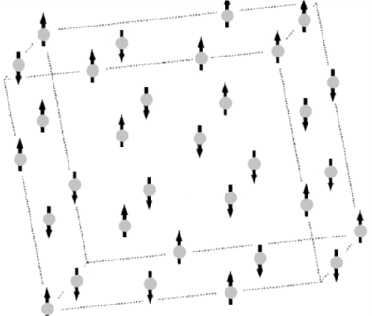
Рис. 1. Магнитная конфигурация суперячейки из 32 атомов железа, использованная для моделирования парамагнитного состояния в ГЦК-железе, обладающая наименьшей энергией. Стрелочками показаны спины атомов железа

Расчёт активности углерода в ГЦК-железе проводился по формуле aС = aconf exp(ΔG/kT), (3) где aС – активность углерода в ГЦК-железе, aconf – конфигурационная часть активности и exp(ΔG/kT) – неконфигурационная часть. Для расчета неконфигурационной части использовались 2 набора данных из работ [11, 12]. При этом, в зависимости от используемого набора, возникали различия в величине неконфигурационного множителя порядка 10–20 %. Нами были взяты данные из работы [11], потому что в них при вычислении экспоненты напрямую использовались экспериментальные данные об активности [19].

Алгоритм вычисления конфигурационной части aconf в деталях описан в работах [11, 12, 20]. Идея метода заключается в следующем. Для каждого члена статистического ансамбля при модели- ровании генерируется лишь часть суммы, виртуальный ввод одного атома углерода при фиксированной позиции других. Эта сумма усредняется, используя обычную Монте-Карло процедуру. Вы- ражение для aconf,

,

M ( N С + 1 )

μ

a conf     , ,

M

Е Е exp i^v; jlk B T ) i = 1 L j = 1

где суммирование по j в ы п ол н яе тс я по в с е м п усты м окта эдриче ским м е ждоу з лиям и по числу шагов i ( i =1, 2, …, M ), и с пол ь з уе м ых в ра с че те м е т одом Монте-Карло; ∆ E j – это из м е не ние в эне рги и си сте м ы, когда в в од итс я о ди н в ирт у а л ь ны й а том углерода; μ = N _Fe – N _C ч и с л о м е ж до уз лий в кр исталле.

Результаты

Дл я н а х ож д ени я э н ерг ии в з а им од ей ст в и я м еж д у а том а м и у гл е рода из э н е ргии с исте м ы с двумя атом а м и уг л е рода в ыч ита ет с я эне рги я д ву х су п е р-ячее к, с оде рж а щ их од иноч ные а том ы уг л е рода , и с ум м ир уе тся с э не ргией бе сприм е с ной су пе ряче й-ки ГЦК-железа:

ΔE = E(Fe32C2) – 2E(Fe32C) + E(Fe32), (5) где E(Fe32C2) – энергия релаксированной супер-ячейки, состоящей из 32 атомов железа и двух атомов углерода, находящихся в октапорах, причем первый атом находится в октапоре, помещенной в начале координат (позиция 0 на рис. 2), а второй атом последовательно помещался в первую, вторую и третью координационную сферу относительно первого (позиции 1, 2, 3 на рис. 2). Отметим, что найденную в нашем случае энергию взаимодействия во второй и третьей координационных сферах необходимо разделить пополам. Это связано с тем, при расчете используются периодические граничные условия, и эти позиции (см. рис. 2), находятся на равном удалении от атома углерода в начале координат и его периодическим повторением возникающем при периодической трансляции ячейки. Энергии взаимодействия между атомами углерода в ГЦК-железе представлены в таблице.

Из таблицы видно, что наблюдается качественное согласие с результатами Монте-Карло моделировании в работе [11]. Отталкивание во второй координационной сфере вдвое больше чем в первой. Чтобы подтвердить работоспособность нашей модели и точность рассчитанных энергий взаимодействия в данной работе сопоставляется кривая активности полученная используя энергии взаимодействия из нашей работы, с экспериментальными данными по активности атомов углерода в ГЦК-железе.

Использовалась система 12 x 12 x 12 элементарных ячеек ГЦК решётки железа [11]. Число шагов Монте-Карло составило 5000. Детальное описание методики и выбора моделирования приведено в нашей работе [15].

Сравнение активности, полученной при использовании энергий взаимодействия, полученных в нашей работе, с экспериментальной кривой активности, представлено на рис. 3. Нами проведены расчёты при Т = 1173, 1273, 1373, 1423, 1573 К, но представлен график только при температуре 1423 К. Решено было ограничиться только одним графиком, потому что в них не было никаких качественных отличий.

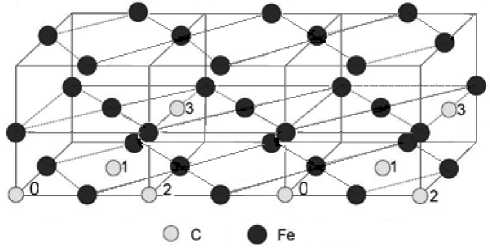
Рис. 2. Расположения атомов углерода в суперячейке из 32 атомов железа, с учётом периодических граничных условий. Новая супер-ячейка начинается от второго атома номер ноль. Атомы железа обозначены чёрным цветом, а углерода – серым

Энергии взаимодействия между атомами углерода в ГЦК-железе

Номер коорд ина цио нно й сферы	Энергия, эВ
1	0,06
2	0,1
3	0,005

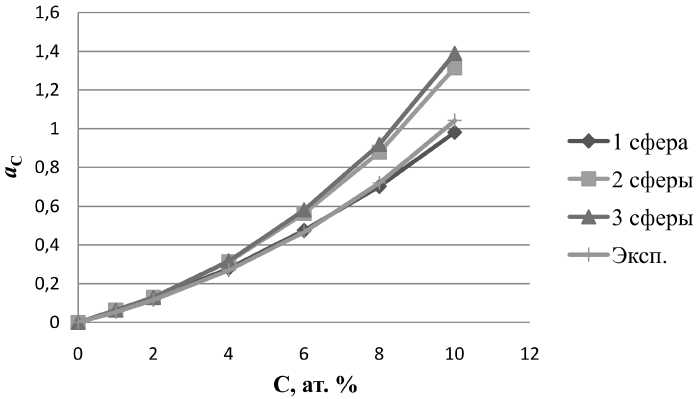
Рис. 3. Зависимость активности углерода в ГЦК-железе от концентрации при Т = 1423 К. Кривые активности получены, используя разное количество учитываемых координационных сфер

Из рис. 3 видно, что наилучшее согласие наблюдается, когда в расчётах использовалась только энергия взаимодействия атомов углерода в первой координационной сфере. Это случайное совпадение открывает нам возможность использования таких расчётов, для быстрых упрощенных расчётов, когда скорость расчётов важнее точности. Не стоит думать, что увеличение числа используемых координационных сфер ухудшает результат, потому что это случайное совпадение.

Когда кривые активности получались при использовании большего количества координационных сфер, согласие несколько ухудшилось, однако по-прежнему оставалось удовлетворительным. Это говорит о достоверности энергий взаимодействия между атомами углерода в парамагнитном ГЦК-железе, полученных в нашей работе, а также о работоспособности нашей модели. Кривые активно- сти, полученные при использовании энергий взаимодействия двух и трёх координационных сфер между атомами углерода, практически не отличаются. Использование данных взаимодействия в третьей координационной сфере не влияет существенно на результаты расчета. Это объясняется очень низким значением энергии взаимодействия между атомами углерода в ГЦК-железе Е3 = 0,005 эВ. Вычисление энергий взаимодействия в следующих координационных сферах невозможно провести в нашей суперячейке. Такие расчёты проведены Пономарёвой [21], показано, что энергия в третьей и последующих координационных сферах близка к нулю, что не повлияет на кривую активности.

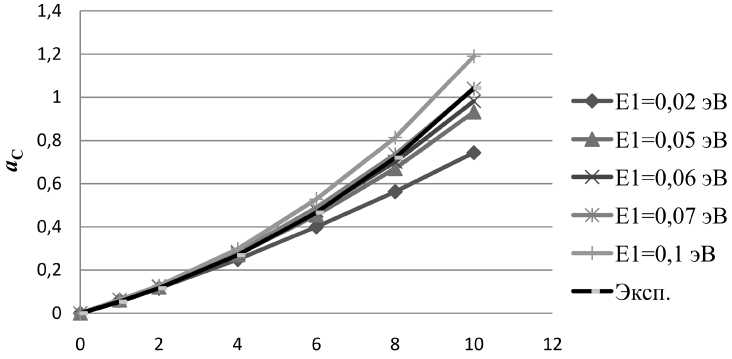
Представляется интересным изучить влияние характера взаимодействия С–С на концентрационную зависимость активности углерода. Для этого проведены расчеты указанной зависимости при

С, ат. %

Рис. 4. Зависимость активности углерода в ГЦК-железе от концентрации при Т = 1423 К. Кривые получены используя разные энергии взаимодействия между атомами углерода в первой координационной сфере

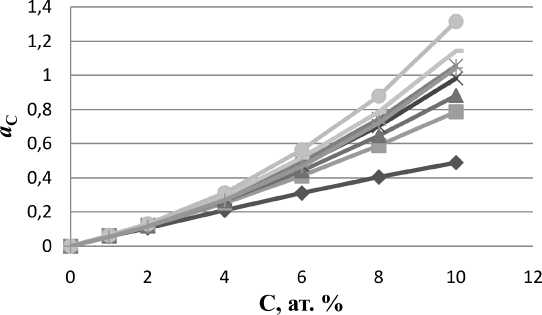
-♦-Е1=0,06; Е2—0Д эВ

• - ■-Е 1=0,06; Е2=-0,04 эВ

• - *-Е 1=0,06; Е2=-0,02 эВ

• - Ж-Е 1=0,06; Е2=0 эВ

• - Ж Е1=0,06; Е2=0,02 эВ

Е 1=0,06; Е2=0,04 эВ

Е 1=0,06; Е2=0Д эВ

Рис. 5. Зависимость активности углерода в ГЦК-железе от концентрации при Т = 1423 К. Кривые получены используя разные энергии взаимодействия между атомами углерода во второй координационной сфере (энергия в первой координационной сфере E 1 = 0,06 эВ)

варьировании взаимодействий в различных координационных сферах. Расчеты проводились в широком диапазоне температур ( Т = 1173, 1273, 1373, 1423, 1573 К), но поскольку качественных отличий в результатах не наблюдалось, далее представлены данные только для температуры 1423 К.

На рис. 4 проанализировано влияние на активность величины энергии отталкивания в первой координационной сфере, пренебрегая взаимодействиями между более удаленными атомами. Видно, что при увеличении энергии взаимодействия кривая активности смещается вверх.

Затем мы изучили влияние на активность величины и знака взаимодействия между атомами углерода во второй координационной сфере при фиксированном значении отталкивания в первой сфере (рис. 5). Аналогично проводились расчеты с варьированием энергии взаимодействия в третьей координационной сфере, при фиксированных значениях взаимодействий в первых двух сферах. Оказалось, что влияние взаимодействия в третьей координационной сфере оказалось незначительным.

Заключение

В данной работе методом первопринципного моделирования получены значения энергии взаимодействия растворенных в парамагнитном ГЦК-железе пар атомов углерода, расположенных в первой, второй и третьей координационных сферах относительно друг друга. Для проверки достоверности значений энергий взаимодействия между атомами углерода в парамагнитном ГЦК-железе, проведён расчёт методом Монте-Карло активности углерода. Показано хорошее качественное согласие полученной кривой активности с экспериментальными данными, что говорит о достоверности данных. Учёт третьей координационной сферы между атомам углерода в ГЦК-железе практически не повлиял на активность углерода. Расчеты методом Монте-Карло с модельными параметрами взаимодействий показали, что усиление отталки- вательного взаимодействие между атомами углерода в любой координационной сфере приводит к сдвигу кривой концентрационной зависимости активности углерода вверх, тогда как усиление притягивающего взаимодействия сдвигает кривую вниз. Это свидетельствует о возможности воспроизведения экспериментальной кривой активности для нескольких отличающихся наборов параметров взаимодействия.

Исследование выполнено за счет гранта Российского научного фонда № 16-19-10252.