Влияние коэффициентов и пределов интегрирования вейвлет-функции Морле на точность результатов анализа гармонических сигналов с нестационарными параметрами

Создание современных высокоточных приборов предполагает решение целого ряда задач, одна из которых заключается в определении параметров нестационарных сигналов, имеющих различные гармонические составляющие. Для их определения применяют либо фильтрацию сигналов с помощью устройств с избирательной амплитудно-частотной характеристикой, либо спектральное разложение в ряд Фурье, либо методы спектрального анализа, основанные на ином математическом аппарате. И если первый подход часто — аппаратное решение задачи в аналоговой форме со всеми присущими ему достоинствами и недостатками, то последние два предполагают цифровую форму представления сигналов с последующей обработкой числовых массивов средствами вычислительной техники. В настоящее время наибольшее распространение получил Фурье-анализ как хорошо отработанный и испытанный многолетней практикой метод анализа. Однако преобразованию Фурье присущи по крайней мере два существенных недостатка: невозможность развертки во времени амплитудных и фазовых характеристик исследуемых сигналов и наличие эффекта Гиббса, заключающегося в искажении величины спектральной плотности вследствие представления функции конечной длительности бесконечными гармоническим функциями.

От этих недостатков свободен интенсивно развивающийся в последнее время представитель третьего подхода анализа сигналов — вейвлет-анализ [1]. Вейвлет-анализ предусматривает представление исследуемого сигнала в виде функций конечной энергии, быстро убывающей во времени. Спектральная плотность вейвлет-функции находится вычислением интеграла вида x 2' a            /X

W(t,a) = — f ф(x)• /1 x—- |dx, a J            I   aJ x/a          \/ z X                    ж            ( X - t )

где ф(x) — исследуемая функция; /II —

I a J вейвлет-функция; x 1 и x 2 — границы интеграла, приведенные к единичному масштабу; t — момент времени, для которого вычисляется значение вейвлет-функции; a — масштаб.

Поскольку величина вычисляемого интеграла существенным образом зависит от вида используемой вейвлет-функции, важной задачей является получение ее аналитического выражения, позволяющего наиболее точно определить параметры исследуемого нестационарного сигнала.

Вейвлет-функцией может быть любая функция конечной энергии, удовлетворяющая условию x2

J / ( x ) d x = 0 .

x ₁

АНАЛИЗ ПОГРЕШНОСТИ АППРОКСИМАЦИИ СИГНАЛА ВЕЙВЛЕТ-ФУНКЦИЯМИ МОРЛЕ

Одной из широко известных вейвлет-функций является функция Морле, описываемая выражением x ²

/ ( x ) = ( cos x + i sin x ) • e k , где k — некоторый постоянный коэффициент.

У вейвлет-функции Морле выделяется реальная (косинусная) составляющая, обозначаемая /Re, и мнимая (синусная) — /Im, а коэффициент к традиционно выбирают равным 50 с пределами интегрирования (1) x 1 и x2, равными ±4п. Такой вейвлет- функцией проведены исследования гармонической функции ϕ(t)=100⋅cos(ω t) с целью определить ее амплитуду. На рис. 1 показано влияние фазы сигнала на погрешность определения амплитуды.

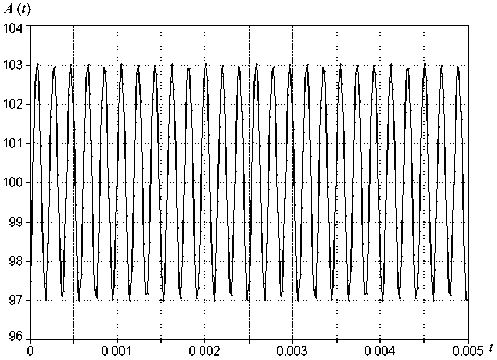
Рис. 1. Зависимость измеренной амплитуды тестового сигнала от его фазы при коэффициенте k = 50 и границах интегрирования ± 4 π вейвлет-функции Морле

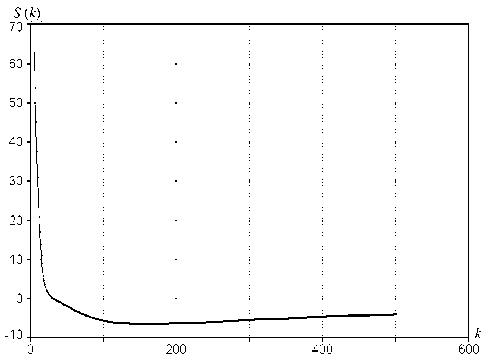
Рис. 2. Зависимость величины интеграла реаль ной части вейвлет-функции Морле от коэффици ента k (пределы интегрирования ± 4 π )

Значения интеграла S от вейвлет-функции Морле, размах изменений измеренной амплитуды и их среднеквадратическое значение при различных пределах интегрирования и значениях параметра k

Пределы интегрирования вейв-лет-функции Морле	Величина параметра k вейв-лет-функции Морле	Значение S интеграла от вейв-лет-функции Морле	Размах изменения амплитуды, при А = 100	Среднеквадратическое отклонение амплитуды, при А = 100
± 4 π	50	5.8	6.0	2.1
± 4.04 π	50	4.1	—	—
± 4 π	30.011	0.005	0.04	0.01
± 4.04 π	30.011	0.2	—	—
± 1.5 π	13.284	0.0007	2.1	0.7
± 1.515 π	13.284	0.06	—	—
± 3.5 π	26.53353	1.3∙10–4	0.08	0.03
± 3.535 π	26.53353	2.0∙10–2	—	—
± 5.5 π	39.485491	2.3∙10–5	0.003	0.001
± 5.555 π	39.485491	2.2∙10–3	—	—
± 9.5 π	65.020128	6.5∙10–6	7.6∙10–6	3.5∙10–6
± 9.595 π	65.020128	5.5∙10–5	—	—

Из анализа рис. 1 следует, что полный размах изменения амплитуды составляет 6 единиц, при заданной амплитуде тестового сигнала в 100 единиц. Невысокая точность определения амплитуды тестового сигнала цифровым методом и зависимость этого значения от фазы исследуемого сигнала связаны с неудачным выбором коэффициента k и границ интегрирования, следствием чего является неравенство нулю реальной части ψ -функции x2

∫ ψ _Re ( x ) d x = S ,                    (3)

x ₁

где ψ Re ( x ) — реальная или косинусная составляющая вейвлета Морле. При традиционных величинах k , x 1 и x 2 интеграл (3), взятый численно, колеблется в пределах 4.1–5.8 (см. таблицу), в то время как интеграл мнимой (синусной) части для симметричных пределов всегда равен нулю вследствие нечетности функции.

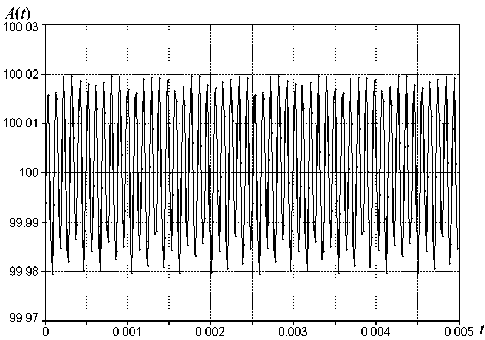
Рис. 3. Зависимость измеренной амплитуды тестового сигнала от фазы сигнала при уточненном коэффициенте k

НАХОЖДЕНИЕ ОПТИМАЛЬНОГО k

Для нахождения оптимальной величины коэффициента k была построена зависимость интеграла реальной составляющей вейвлет-функции Морле от собственно коэффициента k (рис. 2). Коэффициент k дает нулевое значение этой функции в точке 30.011. При этом значение интеграла (3) S находится в пределах 0.005–0.2, что значительно лучше предыдущего случая. Измеренная амплитуда тестового сигнала для уточненного коэффициента k представлена на рис. 3.

Рис. 3 показывает, что полный размах отклонения амплитуды с использованием уточненного коэффициента k составляет уже 0.04. Приведенные зависимости доказывают, что погрешность определения амплитуды гармонического сигнала зависит от значения интеграла (3). Чтобы иметь более полную картину влияния границ интегрирования вейвлет-функции Морле на точность определения амплитуды, необходимо рассмотреть поведение функции cos x вблизи различных границ интегрирования.

НАХОЖДЕНИЕ ОПТИМАЛЬНЫХ ГРАНИЦ ИНТЕГРИРОВАНИЯ

Пределы интегрирования ± 4 π выбраны не совсем удачно, т.к. при этом косинус "обрывается" на максимуме, а при цифровом представлении исследуемого сигнала пределы интегрирования невозможно выдержать точно (они будут выдержаны с точностью до одного кванта дискретизации по времени). Неточность установки пределов интегрирования и приводит к возникновению гармонических колебаний на графике амплитуды (рис. 1, 3).

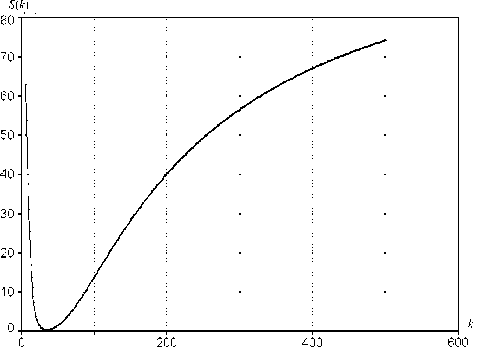
Рис. 4. Зависимость величины интегрирования реальной части вейвлет-функции Морле от коэффициента k в пределах интегрирования ± 4.5 π

Таким образом, можно остановить свой выбор на границах интегрирования, в которых функция y = = cos x имеет значение, близкое к нулю. Такие границы имеют следующие значения: ± 1.5 π ; ± 2.5 π ; ± 3.5 π ; ± 4.5 π ; ± 5.5 π и т.д. Зависимость реальной части вейвлет-функции Морле от параметра k при границах интегрирования ± 4.5 π видна на рис. 4.

Эта зависимость имеет ярко выраженный минимум, но нулевого значения функция не достигает. Подобное поведение зависимости S ( k ) наблюдается и для пределов интегрирования ± 2.5 π . Для границ ± 1.5 π ; ± 3.5 π ; ± 5.5 π зависимость S ( k ) приведена на рис. 5.

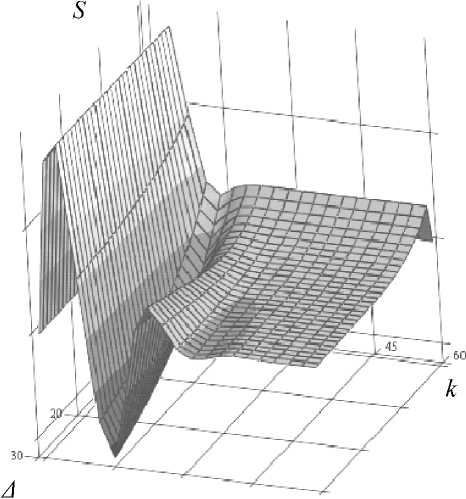
а

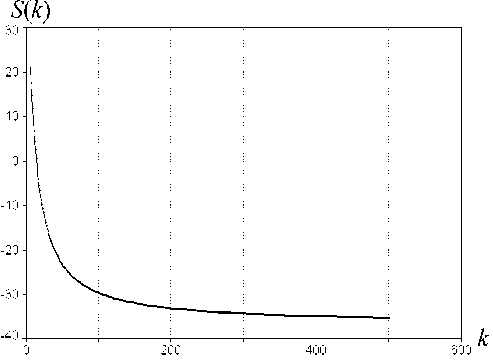
б

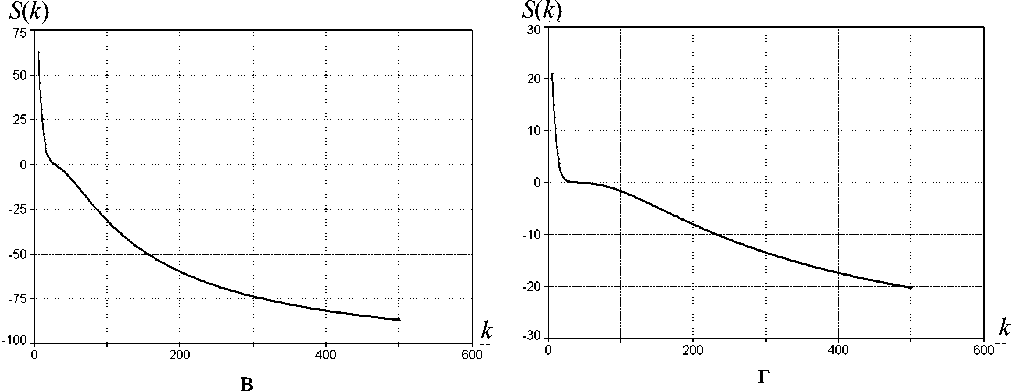
Рис. 5. Зависимость S ( J , к ) от пределов интегрирования J и коэффициента к (а). Сечения: зависимость S ( к ) для пределов интегрирования ±1.5п (б), ± 3.5 п (в), ± 5.5 п (г)

Анализируя зависимости, представленные на рис. 5, следует иметь в виду, что конечная точность цифрового представления вейвлет-функции приведет к отклонению от оптимального значения коэффициента к. В этом случае существенную ∂S ∆S роль играет отношение — =   , которое опреде-

∂k ∆k ляет величину погрешности вычисления вейвлет- функции ∆S в зависимости от точности представле- ния ∆k коэффициента k. Т.к. ΔS =   Δk , для мини-

∂k мизации ошибки следует выбирать величину

∂ S ∂ k

возможно меньшей. Если сравнить рис. 4 и 5, г, то можно заключить, что выбор пределов интегрирования ± 5.5 π обеспечивает лучшую устойчивость к погрешности цифрового представления вейвлет-функции, чем использование пределов ± 4.5 π .

Величины коэффициента k и интеграла (3) для различных пределов интегрирования приведены в таблице.

Большой интерес представляет зависимость оптимального значения коэффициента k от пределов интегрирования вейвлет-функции Морле (рис. 6).

k = 3.789548 + 6.4582414∙ x

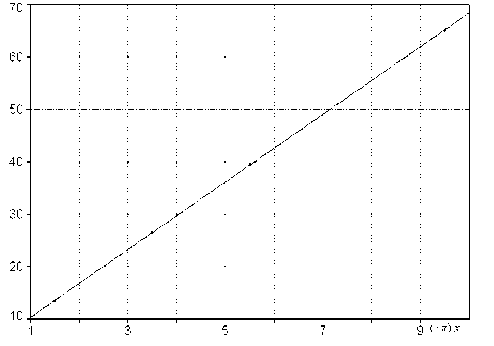
Рис. 6. Зависимость оптимального значения коэффициента k от границ интегрирования вейвлет-функции Морле

ЗАВИСИМОСТЬ ОПТИМАЛЬНОГО k ОТ ПРЕДЕЛОВ ИНТЕГРИРОВАНИЯ

На рис. 6 прослеживается прямолинейная зависимость оптимального значения коэффициента k от пределов интегрирования вейвлет-функции Морле, построенная по данным из таблицы. Эта зависимость становится еще более интересной, если заметить, что на данной прямой лежат и уточненное значение коэффициента k для традиционных пределов интегрирования ± 4 π , и минимумы коэффициента k для границ ± 2.5 π и ± 4.5 π . Существование такой зависимости позволяет легко переходить от одних границ интегрирования к другим. Такой переход полезен, например, при уточнении коэффициента k при "плавающих" вследствие дискретности цифровых сигналов пределах интегрирования вейвлет-функции Морле.

ЗАКЛЮЧЕНИЕ

В заключение нелишним будет упомянуть о главном недостатке вейвлет-преобразований — большом объеме вычислений. Этот недостаток существенно снижает диапазон их практического применения, а величина границ интегрирования существенным образом сказывается на времени вычислений параметров гармонического сигнала. Поэтому при выборе границ интегрирования необходимо помнить о сохранении оптимального соотношения погрешность/время преобразования. Практический опыт использования подобных методик анализа позволяет рекомендовать пределы интегрирования ±5.5π для вычислений с погрешностью не более 0.1 %. Пределы интегрирования ±1.5π приводят к появлению большей погрешности, а пределы ±7.5π и ±9.5π существенно увеличивают вычислительные затраты.

Модифицированная вышеописанным образом вейвлет-функция Морле была использована при обработке сигналов в ряде задач, таких как определение параметров акустической волны в жидких средах, определение периодов сокращения сердечной мышцы, сдвига фаз между двумя гармоническими сигналами и др.

В процессе решения этих задач была отмечена высокая точность определения параметров гармонических сигналов и крайне низкое влияние дестабилизирующих факторов на точность определения этих параметров.