Влияние концентраторов напряжений на механическое поведение магниевого сплава при высокоскоростной деформации в температурном диапазоне от 295 до 673 К

ВЕСТНИК ПНИПУ. МЕХАНИКА № 1, 2019PNRPU MECHANICS BULLETIN

Легкие сплавы на основе магния, относящиеся к изомеханической группе сплавов с гексагональной плотноупакованной решеткой, обладают повышенными удельными прочностными характеристиками и применяются для создания металлических легких и надежных конструкций [1-4]. Повреждаемость сплавов, обусловливающая развитие вязкого разрушения, накладывает ограничения на технологические режимы формования изделий, равноканального углового прессования, рифления при прессовании для получения сплавов с уль-трамелкозернистой структурой [5-7]. Развитие вязкого разрушения магниевых сплавов в широком интервале температур и скоростей деформации является основой технологических процессов обработки изделий, включая резание и раскрой листового проката [8-9]. Для прогноза вязкого разрушения и влияния повреждений на пластическую деформацию магниевых сплавов предложены многопараметрические модели и критерии разрушения в широких условиях нагружения [10-21]. Получены экспериментальные данные о закономерностях деформации магниевых сплавов в широком диапазоне температур и скоростей нагружения [2, 3, 8-22]. Установлено, что магниевые сплавы обладают различным сопротивлением пластическим деформациям при растяжении и сжатии. Этот эффект обусловлен механизмами пластического течения, связанными с двойникованием [19-21]. Обнаружено, что в магниевых сплавах при пластической деформации возникает деформа- ционная анизотропия, обусловленная формированием текстуры [18-20]. При пластической деформации магниевых сплавов в температурном диапазоне от 423 до 673 К происходит интенсивная динамическая рекристаллизация, сопровождающаяся изменением механических свойств [16, 22]. Экспериментальные данные свидетельствуют о том, что механическое поведение магниевых сплавов в широком интервале температур и скоростей деформации отличается от поведения сплавов, относящихся к другим изомеханическим группам [1]. В связи с этим актуальной задачей является разработка адекватных моделей механического поведения магниевых сплавов, учитывающих закономерности пластического течения и разрушения.

В настоящее время большое внимание уделяется разработке моделей со связанными критериями повреждения и пластичности [24-33].

В этих моделях описание пластической деформации связано с расчетными значениями параметра повре-жденности, зависящего от относительного объема пор в материале. Данный класс моделей развивается в рамках подхода Гурсона – Твергарда-Нидельмана [25-30]. Для калибровки этих моделей используются экспериментальные данные, полученные при испытаниях образцов на растяжение, сжатие, сдвиг, продавливание [28-29]. Методики испытаний образцов с различной геометрией были разработаны для получения экспериментальных данных о влиянии трехосности напряженного состояния на пластическое течение и развитие повреждений в области положительных напряжений [20, 28, 32-35].

Цель данной работы заключалась в получении новых экспериментальных данных о влиянии параметра трехосности напряженного состояния на механическое поведение магниевых сплавов Mg-Al-Zn в условиях высокоскоростной деформации и в широком диапазоне температур для калибровки определяющих соотношений, а также в получении новых экспериментальных данных о скоростной чувствительности напряжения течения сплава при повышенных температурах.

1.    Материал и методы исследования 1.1.    Материал

Исследования проведены на коммерческом тонколистовом прокате магниевого сплава МА2-1 (аналог сплава AZ31 или Mg - 3%Al - 1%Zn). Сплав находился в поликристаллическом состоянии. Зеренная структура сплава исследована на сканирующем микроскопе TESCAN методом дифракции вторичных электронов (EBSD). Анализ полученных сканов проведен с помощью лицензионного программного обеспечения HKL Channel 5 Oxford Instruments. Структура являлась мелкокристаллической, однородной и равноосной. Средний размер зерна сплава составлял 40 мкм.

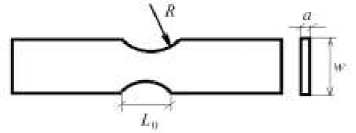
Образцы для испытаний вырезались электроискровым методом на станке с числовым программным управлением DK7732, с ориентацией оси вдоль направления проката из листа толщиной 2,4 мм, что обеспечивало высокую точность воспроизводства геометрических параметров рабочей части образцов. Геометрические параметры образцов для высокоскоростных испытаний были выбраны в соответствии с рекомендациями INSTRON и стандартов ASTM E8 и DIN 50125-H. Геометрия образцов показана на рис. 1.

а

б

Рис. 1. Плоские образцы магниевого сплава с надрезами: а – конфигурация надрезов рабочей части образцов; б – фотографии образцов с надрезами радиусом 2,5, 5, 10 мм

Fig. 1. Flat samples of the magnesium alloy with notches: geometry of notches ( a ); photos of the samples with notches having a radius of 2.5 mm, 5 mm, and 10 mm, respectively ( b )

• 1.2.    Механические испытания и анализ данных

  Для исследования механического поведения тонколистового проката магниевого сплава были проведены испытания по осевому растяжению образцов с постоянной скоростью деформации. Испытания проведены на высокоскоростном испытательном стенде INSTRON 8800 (конфигурация VHS 40/50-20). Для высокоскоростных испытаний применялись образцы, показанные на рис.1. Для проверки воспроизводимости результатов испытывали не менее пяти образцов с одинаковой конфигурацией рабочей части при комнатной температуре (295 К) и при повышенных начальных температурах (473±2) К и (673±2) К. Повышенные температуры во время испытаний были достигнуты путем нагрева рабочей части образцов в теплоизолированном боксе с помощью плоских инфракрасных керамических нагревателей. Нагрев образцов до заданных начальных температур занимал в среднем от 60 с до 160 с, что препятствовало протеканию рекристаллизации сплава. Однородность поля температуры в рабочей части образца обеспечивалась применением потоков инфракрасного излучения по нормали к плоскости образца. Температура на границе рабочей части образца измерялась непрерывно в реальном времени с помощью контактной хромель-алюмелевой термопары с разрешением 0,1 K и точностью 1,5 K.

Испытания выполнены при постоянных скоростях растяжения 20 и 2 м/с, которые обеспечивали скорости деформации 1000 с–1 и 100 с–1 соответственно. Скорость растяжения поддерживалась постоянной с точностью до 0,01 м/с и контролировалась в процессе нагружения образцов в каждом эксперименте. Механические отклики, полученные в результате испытаний на растяжение, получены в виде зависимостей усилий деформирования от перемещений. Эти данные были использованы для определения зависимостей истинных напряжений от истинных деформаций в соответствии со стандартом ASTM E8.

Истинное напряжение σ true определялось по формуле

» true =^ P ( 1 + A l „/ l 0 ) ,               (1)

F 0

где Δ P – приращение усилия; F 0 – площадь начального поперечного сечения рабочей части образца; Δ l cp – удлинение рабочей части образца; l 0 – начальная длина рабочей части образца.

Истинная деформация ε true определялась по формуле

8 _true = 1П(1 + A l ,/ l o ).                  (2)

Относительное равномерное удлинение (δ p ) [%]

определялась по формуле

5p = 1n(A lcp/1o)1OO%, где Δlcp – удлинение рабочей части образца до образования шейки; l0 – начальная длина рабочей части образца.

При проведении испытаний на растяжение датчики позиционирования и ускорения испытательного стенда Instron VHS 40/50-20 обеспечивали определение пластических деформаций в диапазоне от 0 до 0,2 с точностью 0,5 %. В интервале пластических деформаций от 0,2 до 1 точность определения пластической деформации составляла ~2 % от измеренной величины.

Для определения деформации до разрушения ε f плоских образцов применялась формула

Б f — V2 / 3 ^£2 + е2 + [—(£1 + е2 )] ,         (4)

I W1   I                 I 51 I где £ — In I —— I, e2 — In I —— I, w 1 - наименьшая изме-l w0 J          I 50 J ренная ширина сечения в области разрушения; w0 -начальная ширина рабочей части образца в зоне надреза; δ1 – среднее арифметическое измеренных значений толщины в отдельных сечениях области разрушения; δ0 – начальная толщина рабочей части образца в зоне надреза.

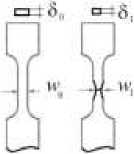
Величины w 1 и w 0 , δ 1 , δ 0 определялись с использованием измерительного цифрового микроскопа БМЦ-1М при анализе фотографий зоны разрушения образцов (рис. 2, а , б ). Ширина зоны и толщина образца были измерены до и после разрушения образца с точностью 1 мкм (см. рис. 2, в ). Толщина δ 1 определялась как среднее арифметическое измеренных значений толщины в отдельных сечениях области разрушения.

При определении деформации до разрушения ε f плоских образцов по формуле (4) предполагалось выполнение постулата пластической несжимаемости и малости упругих деформаций по сравнению с пластическими:

Ej+e2+e3— 0, s3 —-(£,+£2),            (5)

где ε i – главные компоненты тензора деформаций , i = = 1, 2, 3.

Истинные напряжения рассчитывались для каждого испытания вплоть до разрушения образца. После начала формирования шейки принималось во внимание, что напряженное состояние становится неоднородным в рабочей части образцов из-за изменения формы рабочей части.

Параметр трехосности напряженного состояния η и параметр Лоде L определялись по формулам [14]

η = ̶ p /σ eq , L = (2 σ II - σ I - σ III )/(σ I - σ III ),       (6)

где  ai —G k<, gii — (1/2)(g i^ j-oy a), аш — det(a у)—

• ^{— a} ii ^a 22 ^a 33 + ^2а 12 ^а 23 ^а 31 - ^a i2 ^a 33 ^{— a} 23 ^a i1 ^{— C} 31 ^C 22 - пер вый, второй и третий инварианты тензора напряжений Коши соответственно; p - давление, р = - G I /3; G_eq -

  эквивалентное напряжение,

  
  

  ^G eq

  
  

2 a UG i - 2CT kk G “ —

^— 4 ^{3 g} ii ; σ ij – компоненты тензора напряжений Коши.

30 x MM

а                                      б                        в                           г

д                е               ж                з                и

Рис. 2. Конфигурация образцов магниевого сплава в зоне разрушения: а – схема оцифровки области разрушения; б – контур области разрушения; в – схема измерения геометрических параметров зоны разрушения; г – начальная конфигурация сечения рабочей части образцов; фотографии зоны разрушения образцов с надрезами, имеющими радиус; д – 2,5 мм; е – 5 мм; ж – 10 мм;

з – с гладкой частью при 473 К; и – с гладкой частью при 673 K

Fig. 2. The geometry of the magnesium alloy samples in the zone of fracture: the scheme of digitizing the fracture area ( a ), a contour the fracture area ( b ), geometric parameters of the fractured zone and initial geometry of cross section samples ( c ); initial configuration of samples; photographs of the specimens fracture zones with notches with radius of 2.5 mm ( d ), f 5 mm ( e ), 10 mm ( f ), with smoothed specimen at 473K ( g ), and with a smoothed specimen at 673 K ( h )

Начальное значение параметра трехосности напряженного состояния η оценивалось по аналитической формуле для образцов с надрезами в плоском напряженном состоянии [29]:

n= ( 1 + 2 a ) / ( 3 V a ² + a + 1 ) , a = In [ 1 + w /(4 R ) ] ,   (7)

где w – ширина образца; R – значение радиуса кривизны надреза.

Значения η при радиусах надрезов 10, 5, 2,5 мм и для образцов с рабочей частью без надрезов равны 0,3997; 0,4455; 0,5029; 0,33 соответственно.

В рамках подхода Гурсона – Твергаарда–Нидель-мана критерий пластичности имеет вид [25, 26]

( ° ² q / ° ² )^{+ 2} q i f ^cosh ( - q 2 p / ² °,) ^{- 1 -} q 3 ⁽ f ^{) 2} = ⁰,   ⁽⁸⁾

где σ eq - эквивалентное напряжение; σ s – напряжение течения; p – давление; q 1 = 1,5, q 2 = 1 и q 3 = 2,25 – параметры материала; f – параметр поврежденности материала.

При отсутствии повреждений критерий (8) эквивалентен критерию пластичности Мизеса. В случае решения динамических задач девиатор тензора напряжений определяется из решения уравнения

DS ij

Dt

2a eJ-

38    ⁸ ij ,

⁸ eq

где D / Dt – производная по времени Яуманна; S – девиатор тензора напряжений Коши, S_y = ° - (1/ 3)°_kk^_y;

8_y - компоненты тензора скорости деформации,

8 p пластическая деформация, T = T + (0.9/ pC )  °y d8p ;

p 0     2     2

T 0 – начальная температура нагружения; ρ – массовая плотность; С p – удельная теплоемкость.

Атермическое напряжение, задаваемое вторым слагаемым в правой части уравнения (10), описывается соотношениями без учета зависимости от скорости деформации и температуры, но с учетом зависимости от степени пластической деформации, отражающей струк- турную эволюцию сплавов.

Связь между эквивалентной пластической деформацией и параметром повреждения в случае вязкого разрушения материала задается функцией пластическо- го потенциала, которая зависит от параметра повре-жденности материала f:

f  fnucl + f rowth , f.ucl =( fN /5N )8 pq eXP {-0,5 [8 pq -8 N )/5N ]2 } ,    (11)

f;rowth =(1 - f )8 kk, где f – параметр поврежденности; εN и sN представляют собой средние деформации нуклеации и стандартное отклонение соответственно; fN – параметр, контролирующий количество зарождающихся пор.

При использовании моделей поврежденной среды локальное разрушение происходит при достижении эквивалентной деформацией критического значения, величина которого зависит от температуры, скорости деформации и параметра трехосности напряженного состояния. Для прогноза предельной деформации до разрушения ε f магниевых сплавов, относящихся к изо-механической группе сплавов с ГПУ-решеткой, использовались феноменологические соотношения

8 f = F 1 (n) F ₂ (8 eq I 8 0 ) F ₂[( T - T ref )/( T „ - T_RE F )], (12)

Определение параметров материала в уравнениях (7), (8) и (9) осуществляется с использованием результатов экспериментальных исследований механического поведения в соответствующих диапазонах изменения температуры, скорости деформации и параметра трех-осности напряженного состояния.

Напряжения течения для сплавов с гексагональной плотноупакованной решеткой (ГПУ) описывались в виде суммы атермического напряжения и теплового напряжения [27]. Модификация определяющего уравнения Зерилли-Армстронга для магниевых сплавов использована в форме

° 5 = ° 5 0 ^{+ C}. 5 (⁸ eq ) n^{1 +} k hp d g ^-

- C 2 exp { - C 3 T + C 4 T ln ( 8 eq 1 8 eq 0 ) } ,

где °₀, C ₅, n , k_h , C ₂, C ₃, C₄ - параметры материала; d g - средний размер зерна; 8_eq = [(2 / 3)8_у8_у ]^1/2;

8  = 1,05 '; 8P =  [( 2/3 )8p 8p]1/2dt - эквивалентная eq 0                     eq      о                 iJ q где F1, F2, F3 – феноменологические функции; 80 = 0,01 с-1; T и Tm - температура деформации и температура плавления соответственно; TREF = 295 К.

В данной работе были приняты следующие варианты феноменологических функций:

F 1 = D 1 + D ₂ exp ( D 3 h ), F ₂ = ( 1 + ( 8 eq 1 8 0 ) D

F3 =(1 + D5 (T - Tref ) / (Tm - Tref )), где D1, D2, D3, D4, D5 – коэффициенты соотношений, являющиеся параметрами материала.

Для определения коэффициентов D 1 , D 2 , D 3 , D 4 , D 5 в соотношениях (13) необходимы экспериментальные данные о механическом поведении материала при варьировании скорости деформации, температуры и параметра трехосности напряженного состояния.

) ,

2.    Результаты и обсуждение

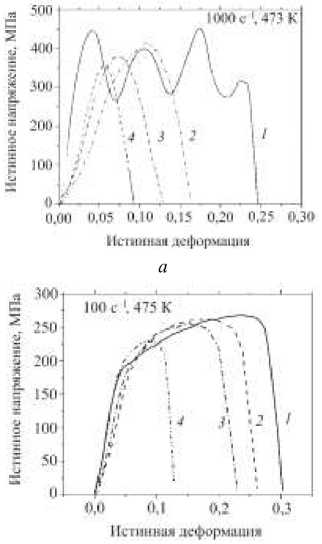
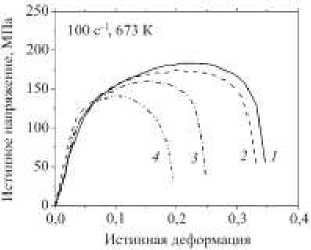
На рис. 3 показаны полученные при обработке экспериментальных данных зависимости истинных напряжений от истинных деформаций при растяжении образ- цов магниевого сплава Mg-3%Al-1%Zn с гладкой рабочей частью (линии 1), с рабочими частями, имевшими надрезы с радиусом 10 мм (линии 2), 5 мм (линии 3), 2,5 мм (линии 4).

Для каждого условия нагружения проводилось по 20 испытаний (4 типа геометрии рабочей части по 5 образцов).

Осциллирующий характер диаграмм деформирования для магниевого сплава МА2-1, показанных линиями 1 на рис 3, а , б , в , аналогичен волнообразному характеру диаграмм деформирования, зарегистрированных для сплава AZ31B в [30]. Формирование осциллирующего характера диаграмм деформирования обусловлено задержкой пластического течения.

в

б

г

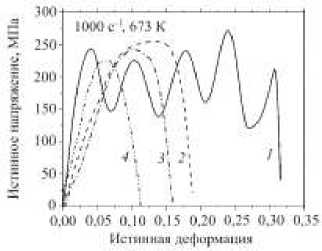
Рис. 3. Зависимости истинных напряжений от истинных деформаций при нагружении образцов магниевого сплава Mg-3%Al-1% Zn со скоростью деформации 1000 с^–1 - ( а ), ( б ) и 100 с^–1 - ( в ), ( г ); линии 1 – для образцов с гладкой частью, линии 2 – для образцов с надрезами, имеющими радиус 10 мм; линии 3 – для образцов с надрезами, имеющими радиус 5 мм; линии 4 – для образцов с надрезами, имеющими радиус 2,5 мм

Fig. 3. True stress – true strain curves of Mg – 3% Al – 1% Zn magnesium alloy at strain rates of 100 s^–1 and 1000 s^–1, the samples with a smooth part ( a ), the samples with notches having a radius of 10 mm ( b ), the samples with notches radius of 5 mm ( c ), ( g ), the samples with notches radius of 2.5 mm ( d )

При скоростях деформации, меньших 100 с–1, осциллирующего характера диаграмм деформирования образцов с гладкой рабочей частью не наблюдается. Осциллирующий характер диаграмм деформирования для образцов с надрезами не наблюдался при всех исследованных режимах нагружения. Анализ полученных результатов, приведенных на рис. 3, свидетельствует о том, что при увеличении скорости деформации от 100 с–1 до 1000 с–1 предел текучести сплава МА2-1 при растяжении увеличивается почти в два раза. Высокая скоростная чувствительность напряжения течения магниевого сплава получена для исследованного диапазона температур от 473 до 673 К. Рост скоростной чувствительности напряжения течения магниевых сплавов с увеличением температуры в диапазоне от 473 до 673 К обусловлен сменой доминирующих механизмов пластического течения с базисного скольжения дислокаций при температуре 473 К на пирамидальное поперечное скольжение дислокаций при температуре 673 К [21].

Диаграммы истинных напряжений от истинных деформаций, показанные на рис. 3 для МА2-1, качественно подобны диаграммам, полученным в [13, 30]. Усредненные значения напряжения течения для сплавов AZ31B и МА2-1 при скорости деформации 1000 с–1 при температуре 473 К различаются на 12 %, а деформации до разрушения – менее чем на 16 %.

Полученные экспериментальные диаграммы истинных напряжений от истинных деформаций, показанные на рис. 3, были использованы для определения численных значений параметров материала в уравнении (10). При определении компонент тензора пластической деформации использовались значения модуля Юнга, E = 43 [1 – 5,3·10^–4( T 295 K)] ГПа [1]. При анализе результатов экспериментов по высокоскоростному растяжению образцов магниевого сплава Mg-3%Al-1%Zn, температура в уравнении (10) оценивалась с использованием линейной зависимости удельной теплоемкости С p от температуры в интервале от 1005,9 Дж/кг K при

295 К до 1130 Дж/кг K при 523 К [13]. Начальная массовая плотность ρ 0 принималась равной 1780 кг/м³. При определении параметров уравнения (10) было использовано значение k hp , полученное ранее в [37]. Полученные значения параметров модифицированной модели Зерилли-Армстронга приведены в таблице.

Параметры модели Зерилли-Армстронга для магниевого сплава Mg-3%Al-1%Zn

Zerilli-Armstrong model parameters for magnesium alloy Mg-3%Al-1%Zn

Параметр модели	с , 0 , ГПа	k hp , Па нм1/2	C 2 , ГПа	C 3 , K–1	C 4 , K–1	C 5 , ГПа	n 1
	0,141	6,2	0,315	0,0029	0,000389	0,505	0,2514

Параметры модельных уравнений кинетики повреждения (11) подбирались для получения согласия прогнозируемых и экспериментальных значений напряжения течения на стадии предразрушения. Были получены следующие значения параметров ε N = 0,1, s N = 0,2, f N = 0,4.

Значения деформации до разрушения материала ε f , полученные при анализе конфигурации зон разрушения образцов, испытанных в указанных на рис. 1 условиях нагружения, были использованы для определения численных значений коэффициентов соотношений (13), являющихся параметрами материала.

Для определения коэффициентов D 1 , D 2 , D 3 , D 4 , D 5 в соотношениях (13) был использован метод регрессионного анализа, реализованный в стандартной процедуре User-Defined Regression Wizard в пакете SigmaPlot 12.5. Показано, что полученные экспериментальные данные могут быть описаны соотношениями (12)–(13).

Зависимость деформации до разрушения для магниевых сплавов Mg–3%Al–1%Zn принимает вид

sf = (0,0199 + 0,5 e"5’4n)(1 + (s^/0,01)-0'0355)x

x ( 1 + 1,6 ( T -295 ) / ( 923-295 ) ) , (14)

где Т - абсолютная температура; s - эквивалентная скорость деформации, имеющая размерность c^–1.

На рис. 4 показаны зависимости деформации до разрушения от параметра трехосности напряженного состояния при заданных температуре и скорости деформации, описываемые соотношением (14).

Полученные в данной работе результаты не имеют точных аналогов, опубликованных ранее в реферируемых журналах.

Отметим, что полученные в данной работе зависимости истинных напряжений от истинных деформаций для МА2-1 качественно согласуются с аналогичными диаграммами для AZ31, полученными авторами [16] при испытаниях цилиндрических образцов магниевого сплава AZ31 (Mg–2,9%Al–0,85%Zn–0,3%Mn) с гладкой рабочей частью в диапазоне температур от 423 до 673 К со скоростями деформации 10–3, 10–2, 10–1, 1, 10, 100 с–1 при растяжении. Для скорости деформации 100 с–1

напряжения течения сплавов AZ31B и MA2-1 в диапазоне деформаций до 20 % при температурах 473 и 673 К отличаются менее чем на 5,5 %. Предельные деформации до разрушения в указанных условиях отличаются на 27 %. Это может быть обусловлено различиями в зеренных структурах сплавов AZ31B и MA2-1.

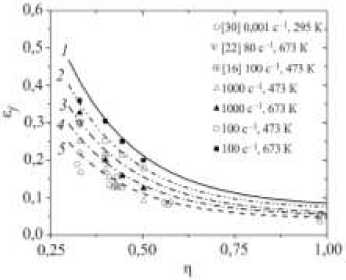
Рис. 4. Зависимость предельной деформации до разрушения при растяжении ε f магниевого сплава Mg-3%Al-1%Zn от параметра трехосности напряженного состояния. Линии 1 , 2 -температуры 673 и 473 К соответственно; скорость деформации 100 с^–1; 3 и 4 – температуры 673 и 473 К соответственно, скорость деформации 1000 с^–1; 5 – скорость деформации 0,001 с^–1, температура 295 К. Символами показаны экспериментальные данные, полученные в [16, 22, 30] и в данной работе

Fig. 4. Strain to fracture depending on the triaxiality stress factor of Mg – 3% Al – 1% Zn magnesium alloy under tension predicted at different temperatures and strain rates (curve 1) - 100 s–1, 673 K, (2) - 100 s–1, 473 K, (3) - 1000 s–1, 673 K, (4) - 1000 s–1, 473 K, and (5) 0.001 s–1 and 295 K. The symbols show the experimental data obtained in [16,22,30] and this research

Результаты, представленные на рис. 4, показывают, что в диапазоне исследованных температур при увеличении скорости деформации от 0,001 до 1000 с^–1 значения деформация до разрушения при растяжении сплавов Mg-3%Al-1%Zn уменьшаются. С увеличением параметра трехосности напряженного состояния от 0,33 до 0,5 величина деформации до разрушения при растяжении сплавов магния Mg-3%Al-1%Zn в исследованных условиях нагружения уменьшается в два раза. Указанный эффект реализуется в широком диапазоне скоростей деформации от 0,001 до 1000 с^–1 при гомологических температурах T / T m от 0,32 до 0,73.

Заключение

Полученные экспериментальные данные свидетельствуют о том, что с ростом параметра трехосности напряженного состояния от 0,33 до 0,5 в диапазоне гомологических температур T/T m от 0,32 до 0,73 деформация до разрушения сплавов магния Mg-3%Al-1%Zn уменьшается почти в два раза при скоростях деформации 100 до 1000 с^–1.

При увеличении скорости деформации от 100 до 1000 с–1 предел текучести сплава МА2-1 при растяжении увеличивается почти в два раза при температурах 473 и 673 К.

Полученные экспериментальные данные о механическом поведении магниевого сплава МА2-1 при скоростях деформации 100 и 1000 с–1 и при температурах 473 и 673 К позволили определить значения параметров материала модифицированной модели Зерилли-Армстронга для ГПУ-сплавов.

Определены численные значения параметров материала для модели, позволяющей описывать зависимость деформации до разрушения магниевого сплава МА2-1 от скорости деформации, температуры и параметра трехосности напряженного состояния.

Полученные результаты могут быть использованы для разработки вычислительных моделей механического поведения конструкций из магниевых сплавов, под