Влияние легирования на термодинамические характеристики водорода в ОЦК-железе

Водородное охрупчивание ОЦК-сплавов на основе железа хорошо известно [1, 2]. Его природа [1–6] связана с выделением газообразного водорода, захваченного расплавом из атмосферы, после кристаллизации массивных деталей в области микроскопических пор, возникающих вблизи протяженных дефектов структуры решетки железа, таких как дислокации и границы зерен. В качестве одного из возможных методов борьбы с указанным явлением может использоваться захват водорода в ловушки, образованные точечными дефектами (вакансиями и атомами легирующих примесей), в областях, где отсутствуют критические дефекты микроструктуры.

Л. Даркен и Р. Смит [7] первыми предположили, что в качестве подобных ловушек могут выступать точечные дефекты кристаллической решетки. Впоследствии было показано, что ловушками водорода являются вакансии, примесные атомы, дислокации, границы зерен, поры и многие другие структурные дефекты [8, 9]. Наиболее удобным и практичным методом управления захватом водорода является использование примесей замещения. Отметим, что благодаря работам В.И. Архарова [10–13] стало хорошо известно о силь- ном воздействии палладия на растворение водорода. Было показано, что малые добавки палладия (< 0,5 ат. %) в значительной мере, если не полностью, подавляют флокенообра-зование. Конечно, палладий как легирующий элемент слишком дорог, однако можно попытаться найти более дешевые и эффективные варианты. Переходные элементы являются перспективными кандидатами для этой цели. Экспериментальная оценка взаимодействия 3d- и 4d-металлов с водородом в железе на основе данных по измерению термодесорбции [14], внутреннего трения [15], мессбауэровской спектроскопии, неупругого рассеяния нейтронов и ионных пучков [3, 8, 9] показала, что многие из них, в частности Ti [16, 17], и Y [18], связывают H атомы. В обзоре [8] приведен ряд данных об опытных значениях величины энергии взаимодействия водорода с примесями в металлах. Во всех случаях полученные в эксперименте значения не превосходят 0,3 эВ. Однако следует отметить, что все упомянутые экспериментальные методы не позволяют достоверно оценить величину энергии захвата атома водорода, поскольку во всех методах данная величина определяется не прямо, а на основе моделей, точность которых может быть оспорена.

В то же время крайне важно оценить влияние примесей на энергию растворения водорода в металле, характеризующую содержание водорода. Такая оценка позволит выявить примеси, способные захватывать водород, не давая ему выделиться в виде пузырьков, что открывает путь к управлению растворимостью водорода и предотвращению негативных воздействий на механическую прочность материалов. Взаимодействие водорода с примесями в металлах может возникать по нескольким причинам. Наиболее существенные из них имеют упругую и электронную природу. К ним следует отнести: а) упругое искажение решетки, вызываемое растворенной в ней примесью; б) различие между взаимодействиями водорода с атомами матрицы и примеси. Остается дискуссионным и вопрос о характере электронного состоянии атома водорода в железе. Существует две противоположные точки зрения: протонная модель (электрон атома Н переходит на свободные электронные уровни матрицы вблизи уровня Ферми, что приводит к положительному заряду иона H) и модель аниона (электроны матрицы захватываются низколежащими водородными уровнями, что приводит к возникновению отрицательно заряженного иона H). Наличие двух различных механизмов приводит к тому, что результаты экспериментального изучения захвата водорода примесями могут иметь различные интерпретации. Из-за наличия двух различных механизмов результирующее поведение примеси может носить достаточно сложный характер, поэтому теория взаимодействия водорода с примесными атомами в ОЦК-железе пока отсутствует. Полу-количественные оценки относительной важности этих механизмов были даны в работах [19, 20]. Эти оценки показали, что для примесей внедрения, таких как азот и кислород, взаимодействие в основном обуславливается упругими эффектами. Для растворов же переходных металлов энергия оба механизма дают примерно равные вклады в энергию растворения водорода. Предсказанная в этих работах энергия связи весьма умерена, как для примесей внедрения, так и замещения, что вполне согласуется с результатами, приведенными в обзоре [8]. Тем не менее, эти оценки не могут считаться последовательной теорией и не могут дать ответ на вопрос, какие именно примеси наиболее сильно связывают атомы Н, поскольку так и не выясненными остались систематические закономерности в поведении энергии захвата от характеристик легирующего элемента. Таким образом, в силу указанных сложностей, последовательная теория взаимодействия водорода с примесными атомами в ОЦК-железе пока не разработана.

Исследование взаимодействия водород-примесь методами современного компьютерного моделирования может обеспечить дополнительной информацией о многих деталях явления, которые затруднительно получить экспериментально. Поскольку величина энергии взаимодействия водорода с растворенными атомами примесей составляет нескольких десятых электрон-вольта, то методика моделирования должна обеспечивать высокую точность расчета. По этой причине методы первопринципного компьютерного моделирования, основанные на теории функционала плотности наиболее пригодны для указанной цели. К настоящему времени проведено несколько расчетов взаимодействия водорода с примесями замещения в металлах [21–24]. В работе [25] было тщательно исследованы наблюдаемые тенденции изменения энтальпии растворения водорода при растворении в самых различных металлах. Систематическое изучение энергии захвата водорода примесями в железе проведено в единственной работе [22] с помощью программного пакета VASP. Было исследовано взаимодействие водорода с примесями замещения 3d-ряда и несколькими примесями 4d-ряда, а также с внедренным примесным атомом углерода. Было показано, что энергия взаимодействия «примесь–Н» коррелирует с электронегативностью примесных атомов и с величиной изменения равновесного объема ячейки ОЦК-железа при замещении одного атома Fe атомом примеси. Однако сильный разброс точек на обеих зависимостях показывает, что эти факторы являются существенными, но не могут рассматриваться в качестве определяющих поведение энергии захвата. Был сделан вывод, что большинство примесей замещения (за исключением Si, Cr, Mn, Co и Mo) захватывают атомы Н, при этом максимальная энергия захвата наблюдается для Y и равна 0,25 эВ. Полученные результаты представляют собой исключительный интерес, однако требуют дополнительной проверки и подтверждения, поскольку расчетные значения энергии захвата представляют собой разность нескольких больших величин и лежат на пределе точности используемого рас- четного метода, использующего PAW-потенциал. В связи с этим в настоящей работе проведены расчеты энергии взаимодействия водорода с sp-, 3d- и 4d-примесями замещения, включая не исследованные в работе [22] примеси Pd и Zr , более точным полнопотенциальным методом линеаризованных сферических волн LAPW, реализованным в пакете WIEN-2k. Кроме того, в результате сравнительного анализа влияния атомов замещения на энергию растворения атома Н, предложены новые характеристики, которые позволяют более точно оценить способность примеси к захвату растворенного в железе водорода.

Детали расчета

Твердые растворы водорода в металлах относятся к категории фаз внедрения, т. е. к растворам, в которых небольшие по размеру атомы водорода размещаются в междоузлиях металлической подрешетки. Моделирование проводилось с помощью программного пакета WIEN2k [26], реализующего метод линеаризованных присоединенных плоских волн (ЛППВ), который является полноэлектронным методом теории функционала плотности. Использовалось приближение обобщенного

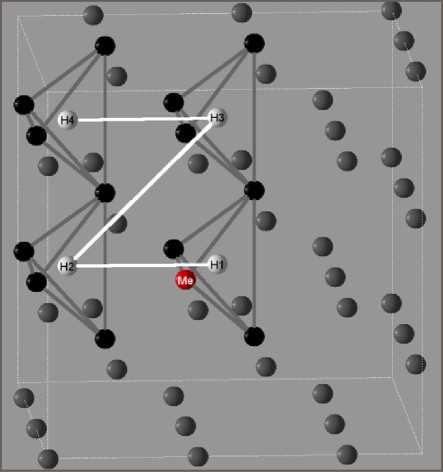
Рис. 1. Суперячейка ОЦК-решетки из 54 узлов. Серыми линиями схематически обозначены тетраэдры, образованные четырьмя атомами железа (черные сферы) или железа с примесным металлом (сфера с символом Me), центры которых являются тетраэдрическими позициями для растворения водорода (белые сферы). Белыми линиями обозначена последовательность удаления атома водорода от примесного металла градиента плотности с обменно-корреляционным потенциалом GGA-PBE96 [27], широко используемым в последнее время в работах по исследованию растворения водорода в α-железе. Суперячейка во всех расчетах состояла из 54 узлов ОЦК-решетки, заполненных 53 атомами железа и 1 атомом примеси замещения (Mg, Al, Si, Sc, Ti, V, Cr, Mn, Co, Ni, Cu, Zn, Y, Zr, Nb, Mo, Pd, Cd), а также внедренного атома водорода. На рис. 1 приведена суперячейка, используемая в расчетах. Символами H1–H4 обозначены ближайшие к примесному металлу неэквивалентные тетраэдрические позиции для растворения водорода.

Были рассчитаны электронная структура, плотность состояний и атомные магнитные моменты суперячеек. Все расчеты были проверены на сходимость величины полной энергии суперячейки и магнитных моментов атомов по отношению к числу k-точек, используемых для интегрирования по зоне Бриллюэна. В качестве начального параметра использовался параметр кристаллической решетки, равный экспериментальному значению для α-железа без примесей (5,41 а.е.) [28], а затем в процессе релаксации кристаллической решетки, этот параметр варьировался и определялся из условия достижения равновесия (минимум полной энергии системы. В работе [24] нами были определены значения основных параметров моделирования, позволяющие с точностью ±0,01 эВ рассчитывать значение энергии растворения водорода в ОЦК-железе. Параметр Kmax, отвечающий за размер базиса, выбирался равным 5,0 а.е.–1, что соответствует энергии обрезания плоских волн, равной 340 эВ. Разбиение первой зоны Бриллюэна производилось на сетку 3×3×3 k-точек, радиус МТ-сфер атомов железа был равен 2,0 а.е., примесных атомов – 2,2 а.е. Проведенные тестовые расчеты показали, что вариация значений радиусов МТ-сфер примесей в переделах ±0,2 а.е. существенно не влияет на результат. В той же работе [24] нами были подтверждены данные из [22] и [28], что атом водорода предпочтительно занимает тетраэдрические поры в решетке α-железа, поэтому основные вычислительные усилия в настоящей работе были направлены на случай растворения водорода в этой позиции в присутствии малых примесей. Тем не менее, было проведено несколько серий расчетов для случая размещения водорода в октаэдрической поре, чтобы убедиться в меньшей стабильно- сти этой позиции даже в присутствии малых металлических примесей замещения. Были исследованы первые 4 окружения каждого примесного металла, когда атом водорода постепенно удалялся отпримесного атома, последовательно занимая тетраэдрические позиции H1–H4 на рис. 1.

Структурная релаксация решетки проводилась в два этапа. На первом этапе проводится оптимизация размеров суперячейки. При объемной оптимизации осуществлялось равномерное расширение и сжатие ( a = b = c ), было рассмотрено по 7 конфигураций для каждого состава с изменением параметра решетки от –1 до +1 % с шагом 0,33 % от экспериментального параметра решетки ОЦК-железа. На каждом шаге изменения параметров решетки проводился отдельный цикл минимизации конфигурации атомов внутри ячейки координат, т. е. проводился поиск стабильной конфигурации с минимальной полной энергией и близкими к нулю действующими на атомы силами. На каждом шаге минимизации проводился самосогласованный расчет электронной структуры. Критерии сходимость во всех расчетах были установлены в 10^–6 эВ для электронных итераций и 10^–3 e^– по заряду, соответственно, а в случае релаксации кристаллической решетки дополнительно использовался критерий сходимости по силам с точностью не менее 2 мРб/а.е.

Как уже отмечалось, мы рассматриваем разбавленные растворы водорода в железе ( х ^ N) , поскольку растворимость его невелика. Для того чтобы оценить влияние на энтальпию растворения возможных взаимодействий H–H, искусственно возникающих из-за периодических граничных условий в методе суперячейки, мы проводили контроль сходимости полной энергии суперячейки для различных размеров (числа частиц) ячейки и показали, что для ОЦК-решетки железа с ячейки 3×3×3, содержащей 54 атома, ошибка не превосходит 0,01 эВ.

Результаты расчетов и их обсуждение

Важной характеристикой в оценке захвата и удержания водорода является энергия его растворения в матрице железа, которая рассчитывается следующим образом:

E diss (H) = E (Fe n - 1 Me H) - E (Fe „ - Me ) -

—2 E [H2( g)]- CD где Ediss(H) – энергия растворения атома водорода в кристалле ОЦК-железа с примесями Ме; E(Fen–1MeH) и E(Fen–1Me) – полные энергии Fen–1MeH и Fen–1Me соответственно; n – число атомов суперячейки, в нашем случае – 54; E[H2(g)] – полная энергия молекулы водорода. Во всех исследованиях энергия E[H2(g)] принималась равной 2,346 Рб, что соответствует общепринятому экспериментальному значению [28]. С учетом релаксации энергия растворения оказалась равной 0,19 эВ/атом, что с высокой точностью совпадает с аналогичным результатом из [28]. Понижение энергии за счет релаксации не является большим (~ 0,10 эВ), что еще раз указывает на привлекательность тетраэдрических пор для водорода. Сохранение положительности энергии растворения и после учета релаксации демонстрирует, что процесс растворения водорода в ОЦК-железе является эндотермическим, что согласуется с наблюдаемой низкой растворимостью H. Согласие с экспериментом может быть улучшено, если принять во внимание квантовую поправку, возникающую при учете энергии нулевых колебаний (ЭНК). В работе [28] была оценена величина энергии нулевых колебаний для водорода, находящегося в тетраэдрической поре железа и для молекулярного водорода. Оказалось, что дополнительный вклад в энергию растворения, связанный с учетом энергии нулевых колебаний, составляет 0,11 эВ. Внесение этой поправки приводит к ЭНК-уточненному значению энергии растворения в 0,30 эВ/атом, что чрезвычайно хорошо согласуется с экспериментальным значением 0,296 эВ/aтом [9].

Моделирование влияния примесей замещения на растворение водорода в ОЦК-железе

На первом этапе компьютерного моделирования был проведен расчет равновесных параметров суперячейки, после введения туда примесей Mg, Al, Si, Sc, Ti, V, Cr, Mn, Co, Ni, Cu, Zn, Y, Zr, Nb, Mo, Pd, Cd и проведения структурной релаксации. Полученные данные, позволили оценить величину объемного эффекта, вызываемого примесями (относительное изменение параметра решетки), что позволило проконтролировать точность проводимых вычислений, путем сопоставления с имеющимися в литературе экспериментальными значениями [29]. Результаты такого сопоставления приведены на рис. 2.

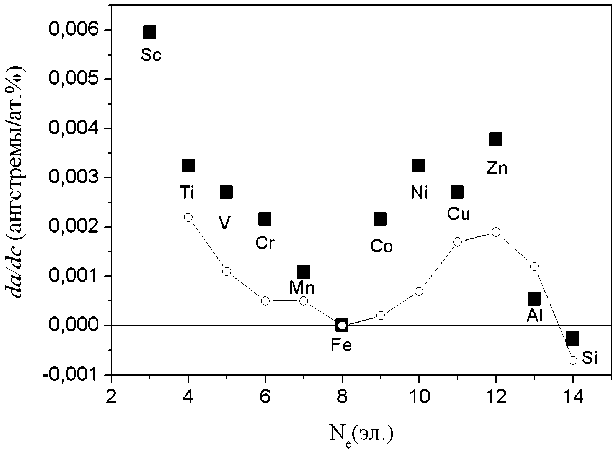
Рис. 2. Расчетные (черные квадраты) и соответствующие экспериментальные изменения параметра решетки железа при легировании da/dc (кружки), построенные как функция числа внешних электронов на примеси N_e

Отметим, что все рассмотренные примеси, кроме Si, увеличивают параметр решетки железа, хотя многие из них имеют меньший ионный радиус, чем атом Fe. Это обстоятельство приводит к тому, что вокруг примесей замещения могут образовываться зоны локального сжатия и растяжения решетки матрицы.

Экспериментально доказано и подтверждено данными ab initio моделирования [28], что в ОЦК-железе атомам водорода энергетически выгодно располагаться в межузельных порах тетраэдрического типа. На втором шаге моделирования мы изучили, не влияет ли на данную тенденцию легирование железа примесями замещения. Поскольку разность энергии растворения водорода в двух различных типах пор достаточно велика (≈ 0,2 эВ), то были проведены расчеты энергии растворения водорода в тетраэдрической и октэдрической позиции ОЦК-решетки железа, находящейся на различных расстояниях от примеси замещения без учета релаксации решетки. Результаты расчетов показали, что энергия растворения водорода в октаэдрических порах, находящихся в ближайших координационных сферах примесей, во всех случаях оказывается существенно выше энергии растворения водорода в тетрапорах, как и в случае ОЦК-железа без примесей. Таким образом, при растворении водорода в ОЦК-железе, рассматриваемые примеси не влияют на предпочтитель- ность тетраэдрической позиции. Поэтому в дальнейшем мы будем рассматривать только расположение атома водорода в тетрагональном междоузлии решетки железа.

Подробные данные об изменении параметров решетки ОЦК-железа при введении атома водорода и примесей замещения как порознь, так и совместно, приведены в таблице. Видно, что растворение водорода наиболее сильно деформирует решетку чистого ОЦК-железа. Это, вероятно, связано с тем, что предварительное легирование железа примесями замещения, которые имеют больший ионный радиус, чем атом железа, уже увеличивает параметр решетки сплава. Вероятно, поэтому растворение водорода в легированном железе деформирует решетку сплава в меньшей степени.

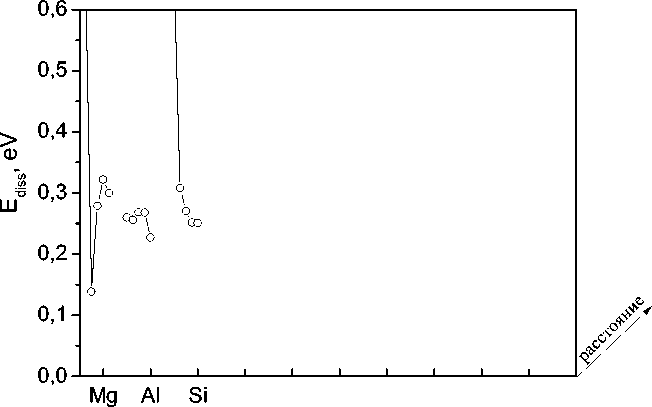
На рис. 3 представлены результаты расчета энергии растворения (по соотношению (1)) водорода в зависимости от положения примеси в периодической таблице Менделеева и различного удаления от нее, начиная от первой до пятой координационной сферы. Отметим, что для тех примесей, где график представленной зависимости в случае ближайшего соседства выходит за пределы рисунка, энергия растворения не могла быть точно определена, поскольку при моделировании атом водорода в процессе релаксации смещался в соседнюю тетраэдрическую позицию второго окружения, преодолевая при этом энергетиче-

Параметры решетки чистого ОЦК-железа и ОЦК-железа с примесями, полученные в результате моделирования

Сплав	Параметр решетки чистого сплава Fe c примесями замещения, Å	Параметр решетки сплава при растворении 1 атома водорода в суперячейке из 54 атомов ( с ≈2 ат. %), Å	Относительное изменение параметра решетки при растворении Н, %	Энергия растворения атома водорода, эВ	Порядковый номер окружения примеси, в которое захватывается водород
Fe54	2,837	2,848	0,191	0,27	–
Fe53Mg	2,842	2,845	0,106	0,14	2
Fe53Al	2,837	2,847	0,352	0,23	5
Fe53Si	2,8365	2,8455	0,317	0,25	5
Fe53Sc	2,848	2,854	0,11	0,06	3
Fe53Ti	2,843	2,849	0,111	0,18	2
Fe53V	2,842	2,848	0,114	0,24	3
Fe53Cr	2,841	2,848	0,131	0,24	3
Fe53Mn	2,839	2,846	0,132	0,27	4
Fe53Co	2,841	2,846	0,080	0,25	3
Fe53Ni	2,843	2,849	0,107	0,24	3
Fe53Cu	2,842	2,847	0,095	0,22	2
Fe53Zn	2,844	2,851	0,128	0,19	2
Fe53Y	2,866	2,868	0,032	0,045	2
Fe53Zr	2,852	2,857	0,087	0,095	2
Fe53Nb	2,849	2,854	0,096	0,19	2
Fe53Mo	2,847	2,853	0,11	0,23	3
Fe53Pd	2,854	2,857	0,11	0,18	2

ский барьер ≈ 0,6 эВ. Видно, что все рассмотренные примеси понижают энергию растворения водорода, т. е. увеличивают его растворимость. Можно видеть, что влияние примесей всех типов на энергию растворения водорода при движении вдоль ряда периодической таблицы демонстрирует определенную тенденцию: положение в тетрапоре, ближайщей к примеси, является наименее стабильным; в ней водород испытывает отталкивание со стороны примеси замещения, которое, вероятно, носит химическую природу. По мере увеличения расстояния, отталкивающее взаимодействие значительно уменьшается. Аналогичные данные о характере взаимодействия ряда примесей замещения с атомами углерода были недавно приведены в работе [30]. Однако из этого общего правила выбиваются случаи примесей Al, Zn, Cd, Nb и Mo. Сплошной горизонтальной линией отмечен уровень энергии растворения водорода в ОЦК-железе без примесей. Величина этой энергии составляет 0,267 эВ, что с хорошей точностью соответствует экспериментальному значению, равному 0,296 эВ [28]. Чаще всего, водород предпочитает находиться в тетрапорах второго окружения, поскольку эта позиция является энергетически самой низкой, однако в ряде случа- ев может захватываться и в более дальних окружениях. По-видимому, это связано с наличием уже упомянутых областей сжатия и растяжения октапор вблизи примесей внедрения. Значения энергии растворения водорода для самого стабильной конфигурации, а также номер координационной сферы, в которой располагалась соответствующая тетрапора, также представлены в таблице.

Полученные нами данные четко свидетельствуют о наличии двух вкладов в энергию растворения водорода, связанную с его взаимодействием с примесями замещения в матрице железа. Первый обусловлен короткодействующей химической связью «водород – примесь», второй вызван действием поля деформаций решетки железа в окрестности примеси. На рис. 4 мы построили зависимость энергии растворения водорода от деформации решетки сплава, вызванной растворением водорода. Отчетливо наблюдается тренд – энергия растворения водорода больше в тех легированных сплавах, в которых растворение водорода приводит к большей деформации решетки. Однако видны и существенные отклонения от общего тренда, которые, вероятно, связаны с возникающими при деформации изменениями электронной структуры.

а)

б)

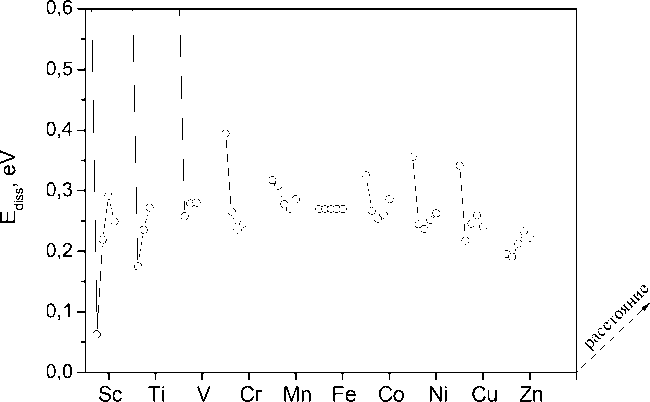
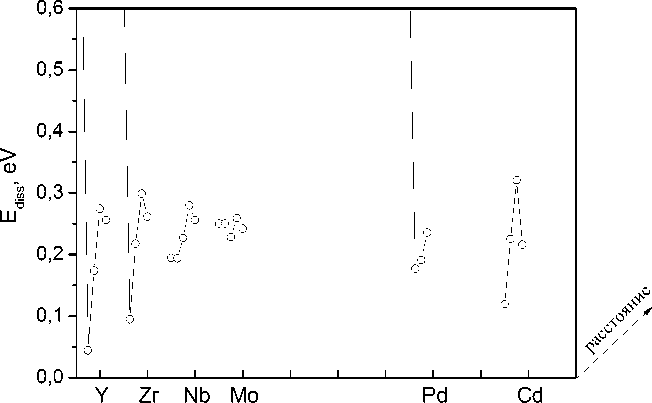
Рис. 3. Энергия растворения атома водорода в ОЦК-железе в тетраэдрических порах, расположенных на различных расстояниях (1-е, 2-е и т. д. соседство) от примеси: s - p -примеси (а), 3 d -примеси (б) и 4 d -примеси (в)

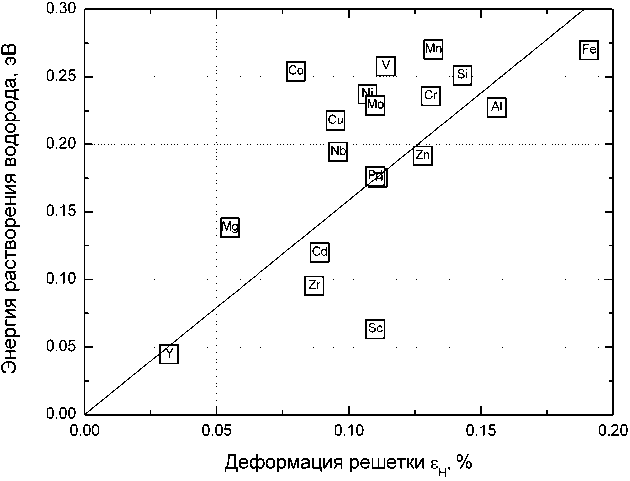
Рис. 4. Зависимость энергии растворения водорода в в ОЦК-сплавах железа, легированных примесями, названия которых указаны в квадратах, от относительной деформации решетки легированного сплава при растворении в нем водорода

Таким образом, вклад поля деформаций

решетки в свою очередь распадается на чисто упругий и электронный вклады в энергию растворения водорода. Несмотря на то, что подобное общее заключение было сделано довольно давно [31], выделить все три вклада

и сравнить их относительную величину –

(рис. 5, д); E _F ⁿ _e ^o ₅ ⁿ ₃ ^re _M ^la _e ^x _H – полная энергия отре-лаксированной суперячейки Fe 53 Me , в тетрапору которой насильственно вставили атом водорода без релаксации размеров и формы суперячейки (рис. 5, г). Нетрудно видеть, что величина E _упр , определяемая (3) имеет смысл

весьма сложная задача.

Для решения данной задачи расчет энергии растворения мы разбили на несколько гипотетических шагов, каждый из которых имеет достаточно ясный физический смысл.

В соответствии с (1) представим энергию

изменения энергии системы в результате упругой релаксации, поэтому может рассматри-

растворения в виде суммы двух вкладов:

ваться как оценка упругого вклада в энергию растворения. Аналогично, величина E _электр , определяемая (4) имеет смысл энергии, которая требуется для переноса свободного атома

relax

E раств   E Fe53 Me H

—

relax E Fe53 Me

—

¹ E h =

2 H 2

= E + E упр электр ;

relax

E упр = E Fe53 Me H

—

nonrelax E Fe53 Me H ;

nonrelax

E электр = E Fe53 Me H

—

relax E Fe53 Me

—

1 _{E ,}

2 H 2 ,

водорода с поверхности внутрь решетки Fe 53 Me , без учета возникающей при этом структурной релаксации (рис. 5, г). Поскольку при таком переносе возмущается лишь электронная подсистема, то такую энергию можно условно назвать электронной.

Электронный вклад в свою очередь удобно разбить на две компоненты:

где E _F ^re _e ^l ₅ ^a ₃ ^x _Me – полная энергия суперячейки, содержащей 53 атома железа и один атом примеси замещения Me , полностью отрелак-

nonrelax

E электр = E Fe53 Me H

—

relax E Fe53 Me

— ¹ E

H 2

сированная, как по параметру решетки, так и по смещениям атомов железа вблизи примеси (рис. 5, в); E _F ^re _e ^l ₅ ^a ₃ ^x _{Me H} – полная энергия отрелак-сированной суперячейки Fe 53 Me H содержащей в тетрапоре решетки один атом водорода

loc         nonloc

= E электр + E электр ^;

loc         nonrelax

E электр = E Fe53 Me H

—

—

relax E Fe53 Me

—

nonrelax relax

‘E Fe54H   + E Fe54 ;

nonloc nonrelax

E электр = E Fe54H

—

relax

E Fe54

— ¹ E h .

2 H 2

	H

а)

г)

Рис. 5. Схемы состояний, для которых проводился расчет полной энергии методом суперячеек, поясняющие разбиение энергии растворения на отдельные вклады: а – идеальная решетка ОЦК-Fe, содержащая 54 атома Fe и один внедренный атом Н (релаксация структуры после внедрения водорода не проведена, в отличие от состояния б); б – решетка ОЦК-Fe, содержащая 53 атома Fe и помещенный в центр тетрапоры атом Н после релаксации структуры; в – полностью отрелаксированная структура Fe53Me; г – отрелакси-рованная структура Fe53Me c внедренным атомом Н (релаксация структуры после внедрения водорода не проведена, в отличие от состояния д); д – полностью отрелаксированная структура Fe53MeН

Здесь EFneo5n4reHlax – величина полной энергии суперячейки Fe54Н без учета релаксации (рис. 5, а), EFreel5a4x – величина полной энергии суперячейки Fe54 чистого ОЦК-железа без примесей. Введенные в (6) и (7) компоненты электронного вклада имеют несколько различающийся смысл. Величина Eloc   есть раз- электр ница энергий внедрения водорода в чистое железо (состояние рис. 5, а) и в ближнее окружение примеси, легирующей железо (состояние рис. 5, г) без учета эффектов релаксации. Ясно, что возникновение различий в энергии растворения Н в основном будет связано с эффектами химической связи между атомом водорода и атомом примеси, и поэтому носит локальный характер. Величина Enonloc эnлoеnктoрc , определяемая как энергия погру жения атома водорода в электронную подсистему чистого железа, связана с нелокальной перестройкой электронной структуры железа при внедрении Н. Заметим, что этот вклад имеет одну и ту же величину для всех примесей.

На рис. 6 приведены результаты анализа различных вкладов в энергию растворения водорода для всех рассмотренных примесей замещения. Поскольку нелокальный электронный вклад во всех случаях одинаков, то величина энергии растворения определяется только упругим и локальным электронным вкладами. Чем эти вклады больше, тем меньше энергия растворения водорода.

Как мы уже отмечали, локальный электронный вклад по смыслу связан с химическим взаимодействием между атомами водорода и примеси. Подтверждением этому служит сопоставление величины этого вклада с энергией образования гидрида элемента, которому принадлежит соответствующая примесь, приведенное на рис. 7. Отчетливо видна корреляция этих величин. Единственным исключением является гидрид никеля, что, возможно, связано с особенностями сверхструктуры этого соединения.

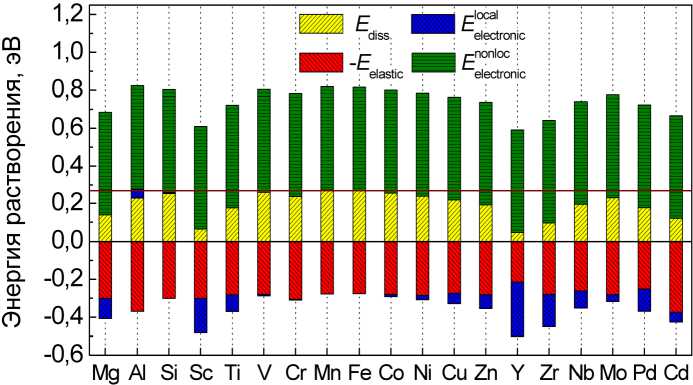
Рис. 6. Вклады в энергию растворения водорода в ОЦК-железе для различных примесей замещения

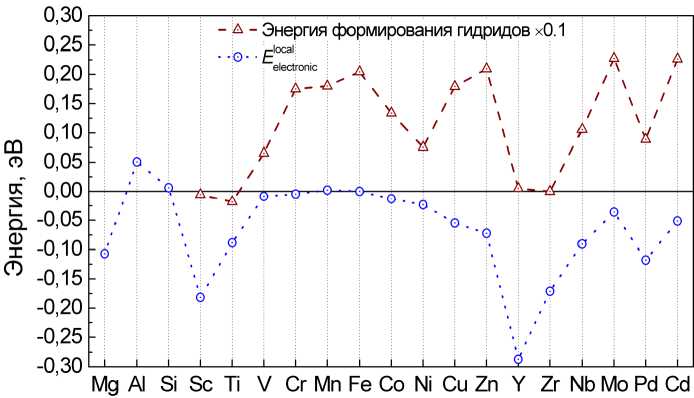
Рис. 7. Сравнение локального электронного вклада в энергию растворения водорода в ОЦК-железе с примесями с энергией формирования гидридов этих примесей

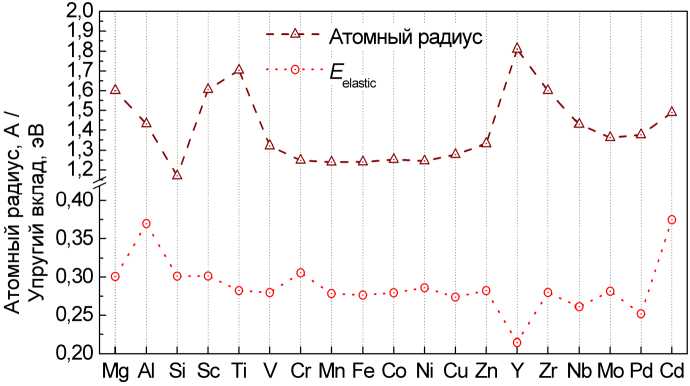
Рис. 8. Сравнение упругого вклада в энергию растворения водорода в ОЦК-железе с примесями с атомным радиусом этих примесей

Четкая корреляция наблюдается также между упругим вкладом в энергию растворения и размером атомного радиуса примеси замещения. Как видно на рис. 8 примеси с большим ионным радиусом, такие как Y, приводят к существенному снижению энергии растворения, и наоборот, элементы с малым ионным радиусом, такие как Al, Si повышают упругий вклад.

Для элементов 3d-ряда, обладающих примерно одинаковыми ионными радиусами, наблюдаются равные упругие вклады. Причину такого поведения можно объяснить следующим образом. Упругий вклад описывает энергию, необходимую для локального расширения решетки при внедрении водорода в тетрапору. Если атомный радиус примеси больше радиуса атома железа, то в своей ок- рестности примесь уже производит расширение решетки, поэтому работа упругого расширения поры водородом понижается. Это полностью подтверждается расчетными данными, приведенными в таблице.

Моделирование энергии связи водорода в ОЦК-железе c примесями замещения

Энергия растворения водорода определяет его равновесное содержание в данном разбавленном сплаве. Для оценки возможности захвата водорода примесями необходима другая энергетическая характеристика-энергия связи. Энергия связи дает информацию о том, насколько сильно примесный атом замещения притягивает атом водорода и может быть рассчитана по следующей формуле:

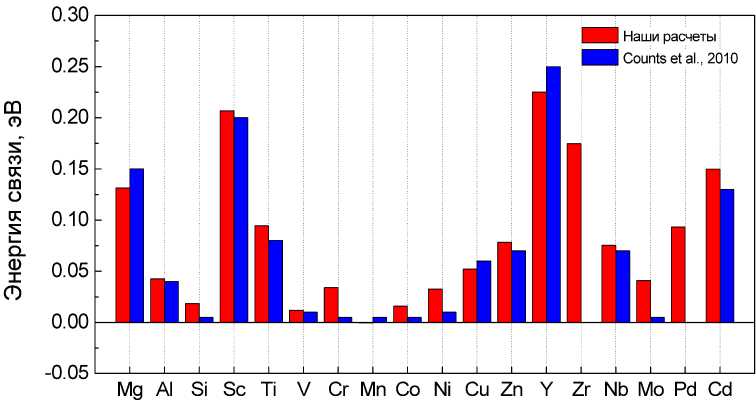
Рис. 9. Сравнение результатов моделирования энергии связи атомов водорода с примесями замещения в ОЦК-железе с данными работы [22]

E св (H– Me ) = E (Fe n H) – E (Fe n –1 Me H), (8) где E св (H– Me ) – энергия связи атома водорода с атомом Ме в ОЦК-железе; E (Fe n –1 Me H) и E (Fe n H) – полные энергии суперячейки состава Fe n –1 Me H и Fe n H соответственно (в нашем случае n = 54).

С использованием выражения (4) нами была рассчитаны энергии связи атома водорода с исследуемыми примесями замещения. Результаты сравнения полученных данных, с результатами первопринципного моделирования, проведенного в работе [22], приведены на рис. 9.

Из рис. 9 видно, что полученная нами энергия связи достаточно хорошо согласуется с результатами работы [22]. Однако нами показано, что хром имеет ненулевую энергию связи, а значит, способен связываться с водородом. Энергия связи водорода с палладием оказалась равной 0,087 эВ, что подтверждает, что атом палладия охотно захватывает водород. Обнаружено, что наибольшими возможностями по захвату водорода обладают примеси Y, Zr и Sc, несколько меньшей энергией обладают ловушки, создаваемые атомами Mg, Pd ,Ti.

В соответствии с (8) энергия связи атома водорода с примесью замещения для 3 d -при-месей по величине близка к разности энергий растворения водорода в чистом железе и в железе, содержащем примеси замещения. Поэтому все факторы, влияющие на энергию растворения, которые мы обсуждали выше, влияют также и на энергию связи.

Выводы

• 1.    С помощью расчетов из первых принципов на основе теории функционала плотности рассмотрено влияние малых примесей замещения Mg, Al, Si, Sc, Ti, V, Cr, Mn, Co, Ni, Cu, Zn, Y, Zr, Nb, Mo, Pd, Cd на энергию растворения водорода в ОЦК-решетке железа.

• 2.    Показано, что даже при наличии указанных примесей в ОЦК-железо энергетически наиболее предпочтительной позицией для растворения водорода остается тетраэдрическая пора.

• 3.    В исследовании обнаружено, что как примеси внедрения, так и замещения заметно изменяют равновесный объем кристаллической решетки матрицы ОЦК-железа, и данный эффект оказывает существенное влияние на энергию растворения водорода и энергию его взаимодействия с примесями.

• 4.    Проведенное исследование позволило определить энергии растворения водорода в октаэдрических позициях ОЦК-железа в зависимости от расстояния до примесей.

• 5.    Полученные в наших расчетах результаты по энергии связи с примесями Ti, Mn, V в целом согласуются с данными [22]. Существенное расхождение обнаруживается для примеси хрома, для которой в [22] получено нулевое значение энергии связи, в то время как в нашем расчете – 0,032 эВ, что значительно лучше согласуется с данными эксперимента. Кроме того, впервые в литературе получено значение энергии связи водорода с примесью палладия, равное 0,087±0,02 эВ.

• 6.    Выяснено, что наибольшей энергией захвата атомов водорода обладают атомы Y, Sc, Zr, Cd, Ti, Mg.

• 7.    Впервые в литературе получено значение энергии связи водорода с примесью палладия, равное 0,087±0,01 эВ.

• 8.    Показано, что поиск примесей, обеспечивающих сильный захват водорода, следует

вести по двум направлениям: как на пути сильной вариации плотности состояний на уровне Ферми, так и на пути локального изменения упругих свойств или свободного объема внутри матрицы.

Исследование поддержано грантом Российского научного фонда №16-19-10252.