Влияние магнитно-импульсной обработки на объем несплошностей деталей летательных аппаратов

Анализ процессов импульсной обработки производится на основе численного моделирования в рамках механики сплошной среды [1]. Используются уравнения, являющиеся следствием законов сохранения массы, импульса и энергии. Замыкается система соотношения- ми упругопластического поведения материала Прандтля-Рейса. В качестве критерия пластичности используется критерий Мизеса. При моделировании МИО электромагнитная сила fi будет входить в уравнения движения.

xi = vt’  VP = Vp; Pvi= °ii,j + fl ’ Pe = ^j ’ °ij =-5ijP + sij ’ f      ^ij^ij

1 p = p( p ,e) ’       i^ ij = O , 5 ( vjj + Vji ) ’ s j ⁺ ^ s j = 1 ц\е,--—

J

2 „2

X —O — упругость; X> O - пластичность ; S ij S ij <  — Y² •

В системе уравнений (1): х_i – координаты материальных частиц, v_i – компоненты вектора скорости, r – плотность, V – объем, е – удельная внутренняя энергия c ij , s ij , z ? ij - компоненты тензоров напряжения, девиатора напряжений и тензора скоростей деформаций соответственно, p - давление, δ _ij – символ Кронекера, m -модуль сдвига, Y₀ – динамический предел текучести.

Численная реализация алгоритма для решения этих уравнений выполняется в рамках явной разностной схемы модифицированных методом типа Уилкинса [2]. В расчетной области строится разностная сетка из треугольных ячеек, в узлах которых определяются значения координат и скоростей, а в ячейках плотность, компоненты тензоров напряжений и скоростей деформаций, внутренняя энергия и т.д. Решение реализуется с помощью программного комплекса KRUG24 ИТПМ СО РАН.

В настоящей работе проводится численное моделирование импульсного воздействия на материал с порами, в частности, ударное воздействие и МИО давлением ИМП (рис. 1).

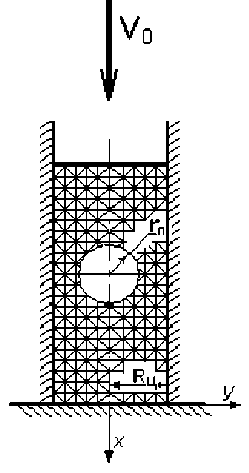
При ударе расчетной схемой является осесимметричный объем (цилиндр) с круглой порой на оси симметрии (см. рис. 1,а). При моделировании импульсной нагрузки с помощью удара цилиндру задается начальная скорость v₀ и он контактирует с жесткой преградой. Бо-

б)

для полного смыкания поры. При этом отмечалось, что время смыкания поры (от начала до

окончания ее пластического деформирования)

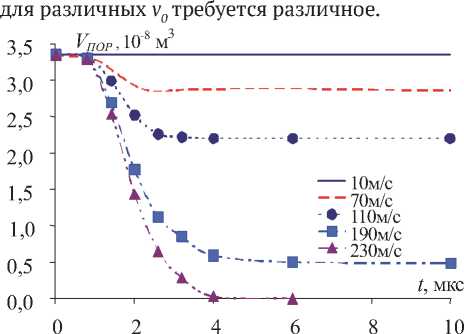
Рис. 2. Изменение объёма поры в Al -сплаве ( а 0 =0,015, Y 0 =300 МПа) при различных скоростях удара

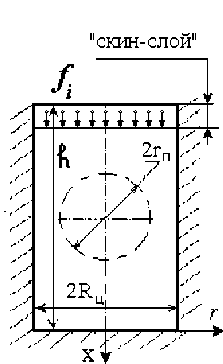
Рис. 1. Расчетные схемы:

а - при ударном воздействии; б - при МИО ковая поверхность также является жесткой. От контактной поверхности цилиндра с преградой распространяется упругопластическая волна сжатия. При подходе к поре волна взаимодействует с ней, и происходит изменение объема поры.

При магнитно-импульсной обработке (см. рис. 1.б) импульсная нагрузка, моделирующая воздействие ИМП, в виде удельной объемной силы (f i ) сконцентрирована в скин-слое, от которого аналогично воздействию поршня передается импульсное воздействие на материал цилиндра. Также возникает упругопластическая волна сжатия, воздействующая на пору. При этом для МИО характерно бесконтактное воздействие и возможность регулирования амплитуды и времени импульсной нагрузки.

Задачи импульсной обработки (см. рис.1) рассматриваются для одной поры. Но можно ввести понятие пористости и использовать коэффициент пористости а , как характеристику материала:

^а = Vno p / ^V ТЕЛА ’                 ⁽²⁾

где V_nop - объем пор в расчетном элементе, V_TMA - объем расчетного элемента. При этом используются: а 0 - исходная пористость и а К - конечная пористость.

При решении задачи удара цилиндра из Al -сплава ( Y 0 =300 МПа) с порой ( а 0 « 0,015) о жесткую преграду определялось изменение объема поры (рис. 2). При малых скоростях воздействие упругое и объем поры не меняется. При увеличении v₀ появляется изменение объема поры, причем остаточное. При достижении определенной скорости удара v₀=v m пора смыкалась полностью. Скорость v m является минимально необходимой

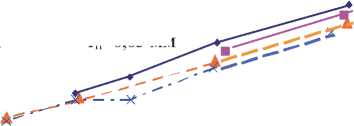
При исследовании зависимости v m ( а 0 ) для абсолютного размера пор установлено, что для различных радиусов пор ( r_n ) в телах с одинаковым коэффициентом пористости ( а ₀ ) примерно одинакова и минимально необходимая скорость удара ( v_m ). Результаты расчетов представлены на рис. 3, из которого видно, что осредненная зависимость v_m от а ₀ практически линейная.

250 -

Vm, м/с гп=0,2 мм гп=0,15 мм ~*~ гп=0,125 мм -х"' Гп=0,05 мм

200 -

50 _ а0

0__,______________________,______________________,____________________,______________________,______________________„

0,004 0,008 0,012 0,016 0,02 0,024 0,028

Рис. 3. Зависимость v m от а о

От момента удара тела с порой о жёсткую преграду до того как пора (поры) полностью или частично сомкнется и перестанет пластически деформироваться проходит определённый промежуток времени (см. рис. 2). Непосредственное время деформирования поры (всех пор), отсчитываемое от начала пластического деформирования до полного смыкания или окончания пластического деформирования, назовем временем смыкания и обозначим как t* .

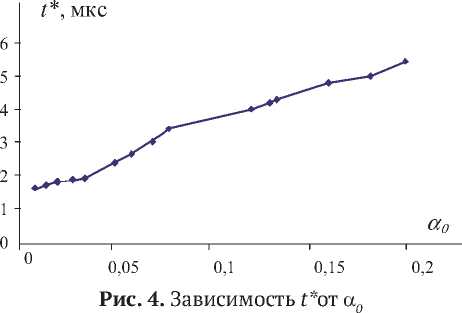
Численные расчеты показывают, что минимально необходимая для полного смыкания скорость удара vm (см. рис. 3) и время смыкания пор t* (рис. 4) зависят линейно от исходной пористости α0 и не зависят от размеров пор. Следует отметить, что это наблюдается как для одной поры, так и для множества пор (3, 6, 9 пор).

Как отмечалось в [1], при интенсивных нагрузках в импульсно нагружаемом элементе (см. рис. 1) шаровая часть ( p ) тензора деформаций ( s_ij ) будет много больше девиаторной части ( s_ij ). Поэтому, часто при описании процесса в качестве характеристики напряженного состояния рассматривается только давление p=p(r,e) .

Изменение давления в зоне поры ( р_П ) при ударе (для v₀ = 170м/с, Y₀ =200МПа, α ₀ ≈ 0,01) показано на рис. 5, где более темные изобары соот-

B(x, y, t) = B m ■ exp - | ■ sin | to t - | (5) ( 0 ₃ ) ( 0 ₃ )

Рис. 5. Типовая динамика развития давления ( p_п ) в зоне поры при ударе

Bm ^2    I   X I   I       X   П i и J(x.y.t) = m c exp\ — . I sin\ tot- — + - I (6) ц0о    ( o3)   (    o3  4)

ветствуют более высоким величинам давления. Фиксируя среднее значение давления в слоях на расстоянии ≤ 0,1 r₀ от границ поры в различные моменты времени t можем построить зависимость р_П ( t ) (рис. 6). На основании зависимостей р_П ( t ) для различных амплитуд нагрузки ( v₀ ) и соответствующего времени смыкания пор ( t* ) (см. рис. 6) в качестве характеристики процесса смыкания пор можно ввести импульс давления в зоне поры ( I_П ), который имеет вид:

I n = J P n (t)dt . (3)

t*

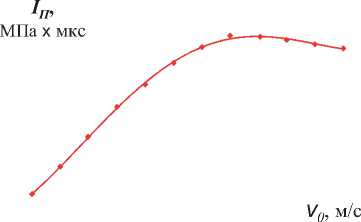
Импульс давления в зоне поры (IП) зависит от исходной пористости, практически линейно возрастая при увеличении α0 (рис. 7). Величина IП также зависит от амплитуды нагрузки, в частности, от величины v0 при ударе. Первоначально при увеличении v0 величина IП возрастает, при достижении v0=vm – минимальной скорости для полного смыкания поры импульс давления в зоне поры достигает максимального значения (рис. 8). При дальнейшем увеличении v0 величина IП уменьшается из-за большего влияния инерционных сил. Таким образом, максимальное значение IП соответствует минимальной нагрузке необходимой для полного смыкания пор. Отметим, что это свойство можно использовать для постановки задач оптимизации.

При моделировании воздействия ИМП (см. рис. 1б) принимаем схему МИО с помощью плоского индуктора (рис. 9).

Электромагнитная сила fl = \j X B\, (4)

как сила, действующая на единицу объема в скин-слое (см. рис1.a), будет входить в уравнение изменения импульса ( p v, = O yj + ft ), где f в общем случае имеет составляющие f_x , f_y , f_z .

Принимается, что сила ИМП действует по оси x , которая совпадает с осью симметрии цилиндрического элемента. Поэтому все составляющие f_i , кроме одной ( f_x ), будут равны нулю.

В соответствии с известными соотношениями для индукции ИМП B(x.y.t) и плотности тока j(x,y,t) [26], –

- уравнение электромагнитной силы f_i имеет вид:

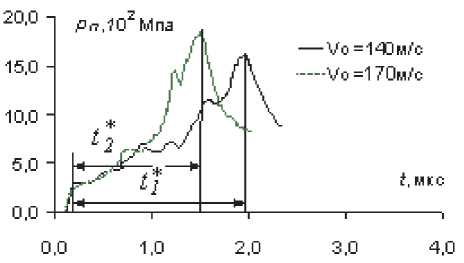
Рис. 6. Зависимость развития давления в зоне поры p_п(t): t₁^* и t₂^* – деформационное время смыкания (при скоростях удара v₀ = 140м/с и v₀ = 170 м/с, соответственно)

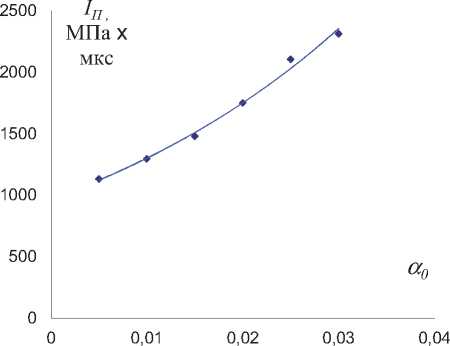
Рис. 7. Зависимость импульса давления смыкания пор I_П от α ₀

50    70    90    110   130   150   170   190

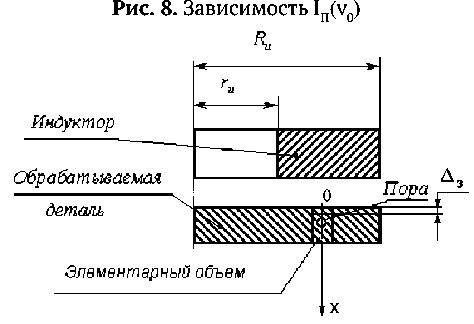
Рис. 9. Схема взаимного расположения детали, содержащей расчетный элементарный объем с порой, и шины плоского индуктора (Rи и rи – внешний и внутренний радиусы шины) при обработке ИМП fx(x,y,t) =

B M Ц о ^ з

\ - 2 x I ■ \ exp —— I sin I tot к ^з J к

x     П I    \         x I ,

---+— I sin I to t --I

S 3 4 J  V     6 3 J , (7)

где В_m – максимум магнитной индукции на поверхности детали; d_З – толщина скин-слоя заготовки; m₀ – магнитная проницаемость вакуума ( m₀ = 1,257 мкГн/м); ω – частота разрядного контура.

Толщина скин-слоя заготовки или индуктора ( d_З,И ), другие величины, входящие в уравнение (7), определяются известными электрическими соотношениями для МИО [3]:

⁶ 3, И   si ²/ ^Ц о ^Y 3, И ^to to

n ^Ц о I m ^ПИ .

Bm =----;------to l p f, (8)

I m

CU ²

; W_H = ~="2" to L = L= + L и - 3

с геометрическими параметрами:

l_P = R_И - г_И ; x ^ 6 ₃ , (9) где γ _З,И – удельная электропроводимость материала заготовки или индуктора, I_m – амплитуда тока; W_Н – накапливаемая энергия заряда магнитно-импульсной установки (МИУ); L – общая индуктивность ( L_C – индуктивность МИУ, L_И-З – индуктивность системы «индуктор-заготовка»); n_И – число витков индуктора; l_P – ширина токовой полосы индуктора.

Индуктивность системы «индуктор-заготовка» вычисляется в зависимости от магнитного объема ( V_M ) по упрощенной формуле, предложенной в работе [3]:

т _ ^Цо У м^ПИ

^LИ - 3 = , . ⁽¹⁰⁾ l_p

Магнитный объем ( V_M ) определяется из следующего выражения:

V M = ^(hB ^{+ 6} И ^{+ 6} 3 ^)SИ , (11)

где h_В – толщина воздушного зазора между индуктором и заготовкой, а S_И – площадь обработки индуктором

В качестве характеристики магнитно-импульсного нагружения используем удельную энергию МИУ:

W* = W hI S и . (12)

Аналогично ударному нагружению при МИО существуют минимально необходимые нагрузки ИМП, при которых достигается полное смыкание пор. Типовой пример изменения динамики объема поры ( α ₀ ≈ 0,01) для Al- сплава ( Y₀ =200МПа) представлен на рис. 10, отражающем динамику сокращения объема поры во времени при различной энергии МИО. Расчеты производились для индуктора c числом витков n_И =1, c шириной токовой полосы l_P =20 мм и с площадью обработки S_И ≈ 22,4 см².

Изменение давления в зоне поры при ударе и при МИО аналогичны друг другу. Зависимости р_П ( t ) для различных амплитуд, времени действия нагрузки при различных методах импульсной обработки, – ударе и МИО, – показаны в виде сравнительных графиков на рис. 11.

На рис.11. представлено: во-первых, развитие давления в зоне поры во времени ( p_П(t) ) на тело с пористостью α ₀= 0,01 при различных скоростях удара v₀ =140м/с – ряд 1, и v₀ =170м/с

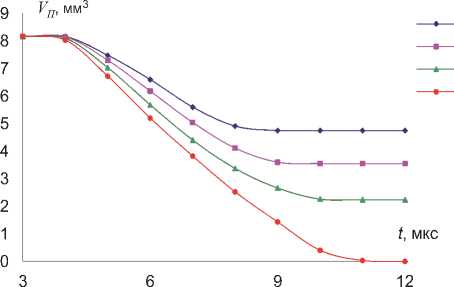
Рис. 10. Динамика изменения объема поры ( a₀ ≈ 0,01) при МИО:

1 – w* =3,21Дж/мм²; 2 – w* =3,57Дж/мм²; 3 – w* =3,97Дж/мм²; 4 – w* ≈ 4,53Дж/мм²

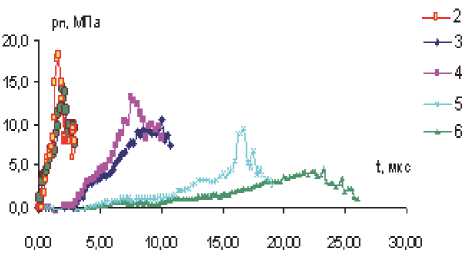
Рис. 11. Развитие давления в зоне поры при ударе: ряд 1 – 140 м/с; ряд 2 –170 м/с;

и при воздействии ИМП:

ряд 3 – t =20 мкс (при W_Н =10,2кДж); ряд 4 – t =20мкс (при W_Н =13,4кДж); ряд 5 – t =36мкс; ряд 6 – t =50мкс

– ряд 2. Во-вторых, сравнивается МИО при различных энергиях заряда МИУ: W_Н =10,2 кДж – ряд 3 и W_Н =13,4 кДж – ряд 4, при одинаковом времени воздействия ИМП (t=20 мкс). В-третьих, для МИО показаны графики p_П(t) при различном времени действия ИМП (полное смыкание пор во всех случаях достигается): ряды 3 и 4 - при t =20 мкс; ряд 5 – при t =36 мкс, ряд 6 – при t =50 мкс.

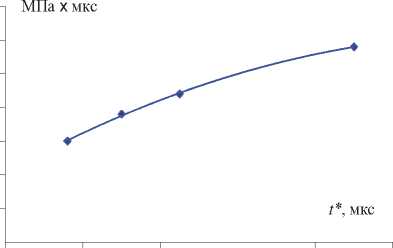
Пользуясь данными p_П(t), представленными на рис. 11, и пользуясь соотношением (3) построим зависимость импульса давления в зоне поры от времени смыкания t* (рис. 12) для величин нагрузок минимально необходимых для полного смыкания пор.

При построении зависимости импульса давления в зоне поры I_П во время её смыкания t* (см. рис. 12) определено, что для более растянутого времени импульсного воздействия величина импульса давления в зоне поры I_П(t*) требуется больше. Это говорит об уменьшении влияния инерционных сил. Это характерно как для ударного воздействия, так и для МИО.

Очевидно, что импульс давления в зоне поры ( I_П ) является характеристикой, объеди-

I n ,

0        2       4        6        8       10

Рис. 12. Зависимость импульса давления в зоне поры I_П от времени её смыкания t*

няющей разные процессы импульсного нагружения. Зависимость I_П(t*) (см. рис. 12) для импульсных нагрузок, минимально необходимых для полного смыкания пор, является единой для удара и МИО. Таким образом, по импульсу давления в зоне поры можно определить характеристику процесса независимо от вида нагружения.

При построении зависимости I_П(w*) (рис. 13) определено, что аналогично зависимости I_П(v₀) (см. рис. 5), импульс давления в зоне поры сначала растет при росте амплитуды импульсной нагрузки, а затем начинает убывать.

При этом максимальное значение I_П соответствует минимальной нагрузке необходимой для полного смыкания пор при МИО. Это свойство импульса давления в зоне поры ( I_П ), как характеристики процесса импульсной обработки, можно использовать для постановки задач оптимизации требуемой величины энергии заряда накапливаемой МИУ.

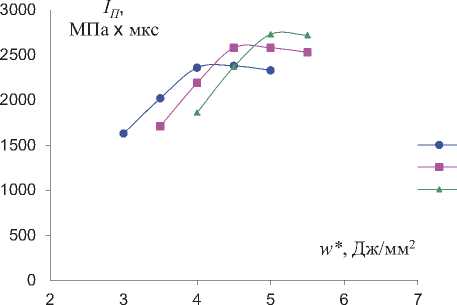
Рис. 13. Зависимость I_П ( w* ) для МИО Al- сплавов при t ≈ 20 мкс: 1 – Y₀ =100 МПа; 2 – Y₀ =200 МПа; 3 – Y₀ = 300 МПа

Для определения энергетических режимов МИО, требуемых для уменьшения пористости, предлагается инженерная методика сведения результатов численных расчетов и оптимизации амплитуды импульсной нагрузки в номограмму (рис. 14). По номо-

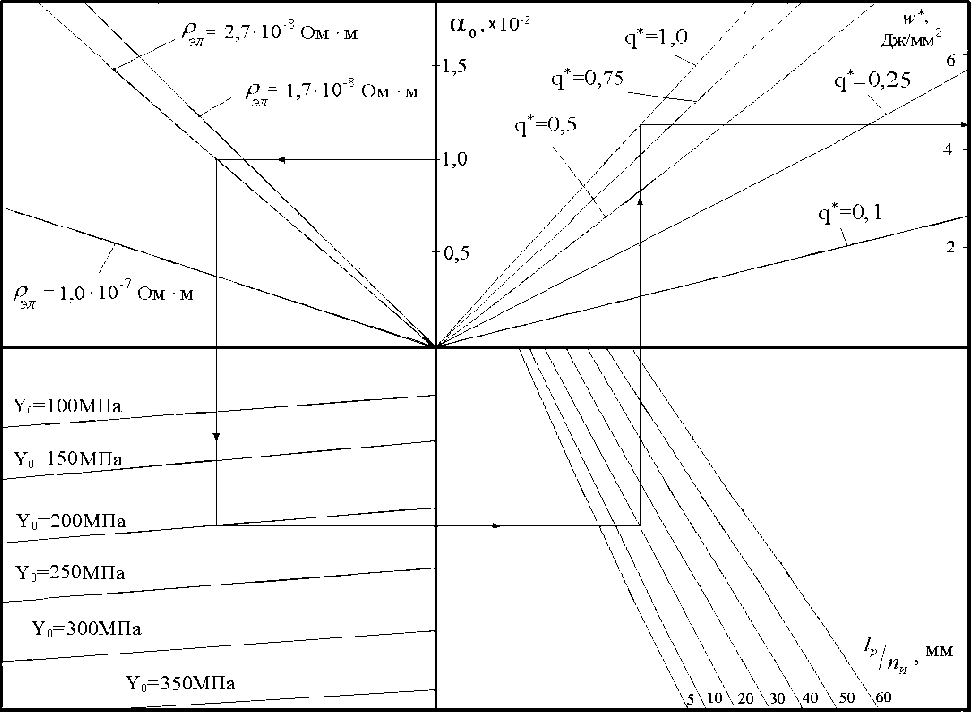
Рис. 14. Номограмма определения энергетических режимов обработки ИМП ( w* ) типовой МИУ (с собственной частотой f_c~20¸25кГц) для различных сплавов сплавов ( r_ЭЛ , Y₀ ) с различной исходной пористостью ( α ₀ ) и заданным коэффициентом смыкания ( q* = 1 – α _К / α ₀ ) при обработке индукторами c числом витков n_И и шириной токовой полосы l_p

грамме в зависимости от свойств обрабатываемого материала ( α ₀ , Y₀ и удельного электрического сопротивления – r_ЭЛ ), параметров индуктора ( n_И и l_p ), требуемой степени смыкания пор ( q* = 1 – α _К / α ₀ ) определяется удельная энергия МИУ, приведенная к площади обработки индуктором ( w* ).

Таким образом:

• -    при численном моделировании импульсной обработки давлением, применяемой для уменьшения объема пор в материалах, определено, что результаты расчетов не зависят от размера и количества пор. Решая задачи об одной поре можно обобщать результаты через коэффициент пористости α ;

• -    введен параметр – импульс давления в зоне поры ( I_П ), который позволяет получать характеристики процесса смыкания пор независимо от способа нагружения;

• -    зависимость изменения импульса давления в зоне поры от амплитуды импульсной нагрузки имеет экстремум. Максимальная величина I_П соответствует минимальной величине нагрузки, необходимой для полного смыкания

пор, что является основой для постановки задач оптимизации;

• -    результаты численного моделирования и оптимизации параметров импульсной нагрузки можно обобщить в виде номограмм для инженерных расчетов по определению требуемых технологических режимов.