Влияние магнитного поля на диэлектрические характеристики в сульфиде марганца, замещенного тулием

В космических аппаратах электроника функционирует в экстремальных условиях, где изменения температур происходят в интервале сотни градусов. Необходимо найти материалы, например, на основе мультиферроиков, которые смогут проявить стабильность работы в этих условиях.

Материалы, в которых проявляется взаимосвязь магнитных и электрических свойств [1–4], магнитоэлектрики и мультиферроики [5–8], представляют интерес как с фундаментальной, так и прикладной точек зрения. Особое внимание привлекают материалы, обнаруживающие магнитоэлектрические свойства в области комнатных и более высоких температур в связи с практическим применением в микроэлектронике для записи и хранения информации. К таким изученным материалам относится феррит висмута BiFeO 3 [9–11]. Эффект гигантской магнитоемкости наблюдался в LuFe₂O₄ [12] при комнатной температуре и объясняется флуктуацией заряда с разной величиной спина в ионах Fe²⁺ и Fe³⁺ в результате снятия вырождения между двумя типами зарядового порядка внешним магнитным полем.

Магнитоемкость в электрически неоднородной среде может быть обусловлена эффектом Максвелла – Вагнера [13] в результате тензорного характера взаимодействия носителей тока с магнитным и электрическим полем и смешивания продольных и поперечных компонент проводимости. В модели магнитоемкость положительна при условии, что размер электрической неоднородности на порядок превышает длину свободного пробега электрона, время измерения 1/ω превышает время рассеяния и матрица является диэлектрической [14].

Как изменится магнитоемкость в электрически неоднородных полупроводниках с компенсацией заряда областей с химическим фазовым расслоением, остается неясным. В этом случае необходимо учитывать подвижность электронов и дырок, кулоновское взаимодействие и рекомбинацию зарядов. В твердых растворах Tm х Mn 1-x S выше комнатной температуры обнаружен магнитоимпеданс, в частности, рост реактивного сопротивления в магнитном поле. Этот эффект может быть обусловлен изменением емкости и индуктивности образца под действием магнитного поля [15; 16].

Цель исследования – установить тип электрической поляризации, механизм релаксации, влияние магнитного поля на диэлектрические характеристики и диэлектрические потери при электронном допировании полупроводников в зависимости от размера электрической неоднородности, которая определяется концентрацией замещения разновалентных ионов.

Результаты и обсуждение

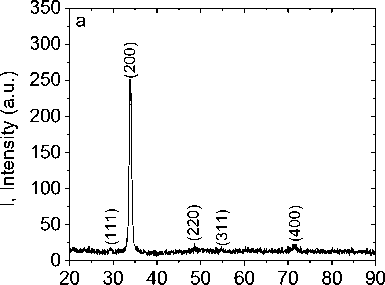
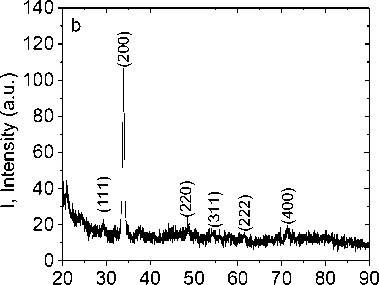
Твердые растворы TmхMn1-xS (0 < x < 0,15) приготовлены методом плавления исходных поли-кристаллических сульфидов марганца и сульфидов тулия [16]. Рентгеноструктурный анализ, выполненный на установке ДРОН-3, установил кубическую решетку типа NaCl. На рис. 1 представлена дифракционная картина твердого раствора TmхMn1-xS. С ростом концентрации замещения марганца ионами тулия интенсивность пиков уменьшается, что связано с некогерентным рассеянием.

2 0, degree

2 0, degree

Рис. 1. Рентгенограммы твердых растворов Tm_xMn_1-xS для концентраций x = 0,05 ( a ), x = 0,1 ( b )

Fig. 1. X-ray diffraction patterns of the Tm_xMn_1-xS solid solutions for concentrations x = 0.05 ( a ), x = 0.1 ( b ).

Диэлектрическая проницаемость и диэлектрические потери определены из измерения емкости и тангенса угла потерь, измеренных на приборе AM-3028, компонентный анализатор в диапазоне частот 102–106 Гц при температурах 300–500 К. Магнитоемкость образца определялась как

_Ae= C ( H ) - C (0)

C (0)

где С ( Н ) – емкость образца, измеренного в магнитном поле Н = 12 кЭ, приложенном параллельно пластинам конденсатора; С (0) – емкость без магнитного поля. Для исключения токов утечки между образцом и пластинами конденсатора помещалась слюда, толщиной несколько микрометров.

Из частотной зависимости диэлектрической проницаемости можно оценить время релаксации и механизм релаксации дипольных моментов [17–19]. Исключение тока утечки позволит оценить вклад миграционной поляризации, обусловленной зарядами в области с химическим фазовым расслоением и размером этой области при приближении к точке протекания ионов тулия по решетке.

На рис. 2 представлены частотные зависимости реальной и мнимой части диэлектрической проницаемости от температуры. На частотной зависимости ε(ω) можно выделить две области частот: низкочастотную ω < ω c и высокочастотную ω > ω c . В низкочастотной области ε(ω) описывается соотношением Дебая с максимумом диэлектрических потерь:

Re( _S ) , + / (2)

1 + ( ЮТ c ) 2

Im( e ) =

X o ^mT c

1 ⁺ ( ЮТ c ^{) 2}

где ε 0 – высокочастотный вклад в проницаемость; χ 0 – статическая восприимчивость диполей. Максимум Im(ε(ω)) смещается в сторону высоких частот при нагревании и время релаксации, найденное из соотношения ωτ c = 1, описывается функцией Аррениуса τ = τ₀exp(ΔE/kT), где ΔE – энергия активации, ΔE = 0,55 эВ. В области высоких частот ω > ω c комплексная диэлектрическая проницаемость линейно зависит от частоты.

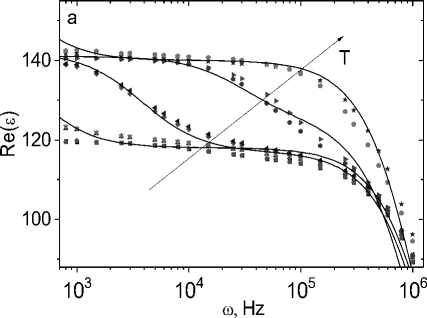
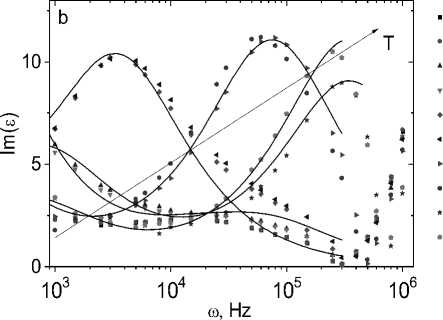
Рис. 2. Действительная Re( ε ) ( a ) и мнимая Im( ε ) ( b ) компоненты диэлектрической проницаемости образца Tm_0.05Mn_0.95S без поля H = 0 кЭ при температурах T = 300 (1), 350 (3), 400 (5), 450 (7), 500 (9) К и в магнитном поле H = 8 кЭ при температурах T = 300 (2), 350 (4), 400 (6), 450 (8), 500 (10) К на частоте ω. Диэлектрическая проницаемость в модели Дебая (сплошная линия) ( a , b )

Fig. 2. The real Re( ε ) ( a ) and imaginary Im( ε ) ( b ) parts of the permittivity of the sample Tm_0.05Mn_0.95S without field H = 0 kOe at temperatures T = 300 (1), 350 (3), 400 (5), 450 (7), 500 (9) K and in magnetic field H = 8 kOe at temperatures T = 300 (2), 350 (4), 400 (6), 450 (8), 500 (10) K on the frequency ω. The permittivity in the Debye model (solid line) ( a , b )

Диэлектрические потери вызваны электрон-фононным взаимодействием. Мнимая часть диэлектрической проницаемости связана с вещественной частью оптической проводимости σ соотношением Im(ε) = σ/ω. В неупорядоченных полупроводниках с прыжковым типом проводимости может реализоваться резонансный и релаксационный механизм проводимости. Если энергия кулоновского отталкивания электронов, расположенных на расстоянии R , меньше тепловой энергии e ²/ε R << kT, то превалирует релаксационная оптическая проводимость [20]:

о ( ю ) = 1 п ² e ² ag ² h m 2 R ⁴,

где а – радиус локализации электрона; g – электронная плотность состояний на уровне Ферми. В этом случае Im(ε) = Аω. Частота кроссовера ω с от Дебаевской релаксации к релаксационной проводимости, связанной с поглощением и испусканием фононов, обусловлена радиусом локализации электрона и электронной плотностью состояний g . Если предположить, что электрон локализован в области химического фазового расслоения, созданного ионами тулия, и радиус локализации не зависит от температуры, то рост ω с выше 400 К связан с увеличением электронной плотности состояний на уровне химпотенциала g ~ T².

В магнитном поле время Дебаевской релаксации увеличивается, точка перегиба Re (ε) и максимум Im(ε) смещается в сторону низких частот. В результате диэлектрическая проницаемость уменьшается в магнитном поле при ωτ = 1 на 0,5, 2,4 и 3,3 % при Т = 400, 450 и 500 К. Более существенные изменения обнаружены в тангенсе угла диэлектрических потерь, который зависит от активных потерь, в результате увеличения рассеяния электронов на локальных деформациях и фононах в области расположения ионов тулия. Диэлектрические потери возрастают на 14 и 36 % при Т = 450 и 500 К и уменьшаются до 15 % в области низких частот при Т = 350 и 400 К.

С ростом концентрации увеличивается радиус локализации электронов, связанных с ионами тулия. На рис. 3 изображены компоненты диэлектрической проницаемости образца Tm x Mn 1–x S от частоты для концентрации х = 0,1. В этих образцах также реализуется Дебаевской и элек-трон-фононный механизм релаксации индуцированной электрической поляризации [21]. При нагревании максимум Im( ε ) смещается в область высоких частот. Энергия активации ΔE = 0,2 эВ (1550 см^–1) в два раза меньше, чем для х = 0,05. Частота кроссовера, найденная из минимума Im(ε(ω)), растет при нагревании образца по степенному закону ω с ~ Т^3/2.

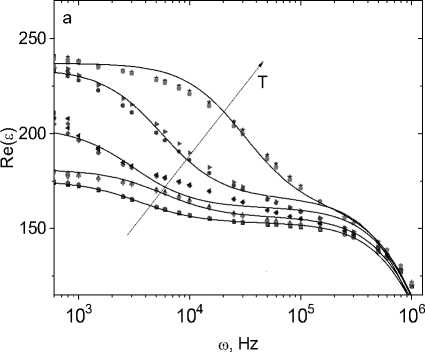
Рис. 3. Действительная Re( ε ) ( a ) и мнимая Im( ε ) ( b ) компоненты диэлектрической проницаемости образца Tm_0.1Mn_0.9S без поля H = 0 кЭ при температурах T = 300 (1), 350 (3), 400 (5), 450 (7), 500 (9) К и в магнитном поле Н = 8 кЭ при температурах Т = 300 (2), 350 (4), 400 (6), 450 (8), 500 (10) К на частоте ω . Диэлектрическая проницаемость в модели Дебая (сплошная линия) ( a , b )

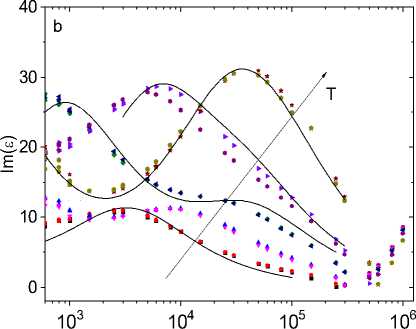
ω , Hz

Fig. 3. The real Re( ε ) ( a ) and imaginary Im( ε ) ( b ) parts of the permittivity of the sample Tm_0.1Mn_0.9S without field H = 0 kOe at temperatures T = 300 (1), 350 (3), 400 (5), 450 (7), 500 (9) K and in a magnetic field H = 8 kOe at temperatures T = 300 (2), 350 (4), 400 (6), 450 (8), 500 (10) K on the frequency ω.

The permittivity in the Debye model (solid line) ( a , b )

Возможно, это связано со смещением химпотенциала по температуре и увеличением электронной плотности g ~ T^3/4. В магнитном поле диэлектрическая проницаемость уменьшается и наибольшее изменение Δε = 2,5 % достигается при Т = 450 К. При остальных температурах магнитоемкость не превышает 0,5 %. Смещение максимума мнимой компоненты диэлектрической проницаемости к низким частотам в магнитном поле приводит к изменению знака диэлектрических потерь с положительного на отрицательное с δ(Im(ε)) = 0,024 до –0,08 при Т = 450 К.

При приближении к концентрации протекания ионов тулия на ГЦК решетке x c = 0,17 [22] частотная зависимость ε(ω) качественно меняется (рис. 4). В интервале частот 10²–10⁶ Гц диэлектрическая проницаемость не описывается в модели Дебая. Протекание обменных связей Tm-Tm по решетке приводит к шунтированию обкладок конденсатора и отсутствию миграционной поляризации на границе раздела ионов Mn-Tm. Рост ε(ω) ниже 100 Гц вызван накоплением зарядов вблизи пластин конденсатора. Мнимая компонента диэлектрической проницаемости уменьшается в магнитном поле до 9 % при Т = 450 и 500 К в результате уменьшения проводимости σ(Н, ω) < σ(0, ω) (рис. 4, с ).

Частота, при которой диэлектрическая проницаемость обусловлена релаксационной проводимостью за счет фононов, не зависит от температуры. Это связано с сохранением электронной плотности состояний на уровне химпотенциала при нагревании. Для концентрации х = 0,15 магнитоемкость отсутствует (∆ε < 0,005). Снижение диэлектрических потерь в магнитном поле вызвано уменьшением проводимости.

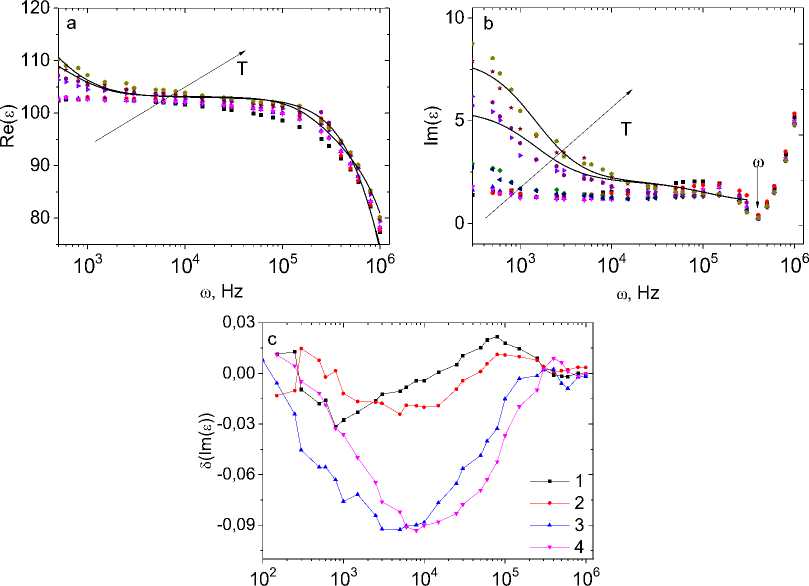
ω , Hz

Рис. 4. Действительная Re( ε ) ( a ) и мнимая Im( ε ) ( b ) компоненты диэлектрической проницаемости образца Tm_0.15Mn_0.85S без поля H = 0 кЭ при температурах T = 300 (1) , 350 (3), 400 (5), 450 (7), 500 (9) К и в магнитном поле Н = 8 кЭ при температурах Т = 300 (2), 350 (4), 400 (6), 450 (8), 500 (10) К на частоте ω. Диэлектрическая проницаемость в модели Дебая (сплошная линия) ( a , b ). Относительное изменение мнимой части диэлектрической проницаемости δ (Im( ε )) в магнитном поле H = 8 кЭ при температурах T = 350 (1), 400 (2), 450 (3), 500 (4) K в зависимости от частоты ω ( с )

Fig. 4. The real Re( ε ) ( a ) and imaginary Im( ε ) ( b ) parts of the permittivity of the sample Tm_0.15Mn_0.85S without field H = 0 kOe at temperatures T = 300 K(1), 350 K(3), 400 K(5), 450 K(7), 500 K(9) and in magnetic field H = 8 kOe at temperatures T = 300 K(2), 350 K(4), 400 K(6), 450 K(8), 500 K(10) on the frequency ω. The permittivity in the Debye model (solid line) ( a , b ). The relative change of the imaginary part of the permittivity δ(Im(ε)) in magnetic field H = 8 kOe at temperatures T=350K(1), 400K(2), 450K(3), 500K (4) versus frequency ω ( с )

Заключение

Диэлектрическая проницаемость в интервале частот до одного мегагерца при электронном допировании в Tm x Mn 1–x S обусловлена миграционной поляризацией локализованных электронов и релаксационной проводимостью. В модели Дебая найдено время релаксации электрической поляризации, которая имеет активационный характер и описывается законом Аррениуса. В окрестности концентрации протекания ионов тулия по решетке исчезает вклад миграционной поляризации и диэлектрические характеристики обусловлены релаксационной проводимостью в области высоких частот, интервал которых не зависит от температуры. В магнитном поле диэлектрическая проницаемость уменьшается на несколько процентов и практически не меняется в образце с концентрацией вблизи концентрации протекания. Увеличение времени релаксации в магнитном поле приводит к сдвигу максимума диэлектрических потерь в область низких частот и смене знака диэлектрических потерь в магнитном поле по частоте. Найдена высокая индуктивность образца в магнитном поле.