Влияние магнитных линз на работу электрического квадрупольного масс-спектрометра

Первое упоминание о квадрупольном масс-спектрометре появилось в далеком 1953 г. [1]. Теория квадруполя, разработанная В. Паулем, вошла в классические учебники по масс-спектрометрии [2]. Но, несмотря на столь долгий срок, до сих пор квадрупольный масс-спектрометр используется в современных лабораториях и в различных технологических процессах. Компактность, простая совместимость, широкое производство, строгая разработанная теория — все это выгодно отличает квадрупольный масс-фильтр от других масс-анализаторов. Однако невысокие разрешающая способность и чувствительность позволяют использовать его только на предварительной стадии анализа. В связи с этим понятны попытки экспериментаторов улучшить разрешение и чувствительность прибора различными средствами, например выбором новых рабочих режимов в зонах стабильности, отличной от первой [3, 4], варьированием высокочастотных и статических мод [5], воздействием магнитного поля [6–8].

Наша работа является частью большого исследования о влиянии магнитного поля на работу квадрупольного масс-спектрометра. История вопроса такова. Один из авторов статьи, В.И. Николаев, экспериментально "нащупал" эффект улучшения работы классического квадрупольного масс-фильтра, прикладывая магниты различной геометрии. Ему удалось увеличить разрешающую способность и приборную чувствительность в несколько раз.

В нашем исследовании мы рассмотрим воздействие небольшого фрагмента однородного магнитного поля, фактически короткой магнитной линзы, установленной в различных точках канала масс-фильтра, на работу прибора.

БЕЗРАЗМЕРНАЯ МОДЕЛЬ ДВИЖЕНИЯ

Для анализа динамики частиц введем безразмерную модель движения. Положим

R = t • r = t ( x i + у j + z k ) , t = T • t ,        (1)

где x , y , z , τ — безразмерные координаты и время, a t , T — выбранные линейный и временной масштабы. В качестве Т выгодно принять период колебаний ВЧ-поля независимо от того, синусоидальное или иной формы. Квазистатический потенциал квадрупольной системы можно записать тогда в виде

Ф =

фо +ф1 • f [ T

X ²

- Y²

t

где Ф о и Ф ₁ — размерные значения потенциала. В безразмерных параметрах (1) потенциал можно записать как

^Ф = [^Ф 0 ^+Ф 1 • f ^{( т} ) ]• ( x ^{2 -} у ² ) ,            (3)

f(т +1) = f(т).

Вектор магнитной индукции запишем в виде

B = B 0 • b = B 0 ( b 1 i + b 2 j + b ₃ k ) ,               (4)

где В 0 — характерное значение индукции внутри прибора (например, максимальное), b — безразмерный параметр. Основное уравнение, описывающее поведение частицы в совмещенных магнитном и электрическом полях, запишется так

^ • r; = -2q [ф 0 + Ф1 • f(т )]x

x(xi -yj) + qB[rX b],(5)

где точками обозначены производные поτ. Приводя коэффициенты к безразмерной форме, получим уравнение вида r = -[Ц + v - f (t)](xi - yi) + Л -[r x b],(6)

где введены следующие обозначения

2 q Ф _о T ²       2 q Ф Т² qB

^         ~ , V — о ,    ^ —       .(7)

m - I            m - ^

Этих соотношений нам достаточно, чтобы провести полный анализ динамики частиц.

КОРОТКИЕ ОДНОРОДНЫЕ ПРОДОЛЬНЫЕ МАГНИТНЫЕ ЛИНЗЫ

Обрезанный фрагмент однородного магнитного поля, вытянутый вдоль оси z, можно рассматривать как некий вариант классической магнитной линзы. В действительности такая линза создается короткой катушкой с током, и распределение на оси z носит не прямоугольный, а колоколообразный характер. Это обстоятельство играет очень важную роль в классической электронной микроскопии, где эти линзы должны строить правильные оптические изображения с низким уровнем аберраций. Если мы накладываем такую линзу на квадрупольный оптический тракт, то ее действие приобретает совсем иной физический характер хотя бы уже из-за присутствия высокочастотного электрического поля. Поэтому нет смысла настаивать на колоколообразном распределении магнитного поля, и вполне можно удовлетвориться разрывной прямоугольной моделью. Вектор безразмерной индукции b однородного магнитного поля, ориентированного вдоль канала, представится в виде b1 — b2 — 0, fo,

Ь з —< 1,

. 0,

0 <  z <  z 1 ;

z 1 <  z <  z 2 ; z >  z 2 ,

z ₂ - z 1 — d .

Роль магнитного поля, когда оно заполняет весь квадруполь, столь же определяющая, как и электрического, поскольку оно участвует в процессе формирования геометрии зон устойчивости и дает вклад в реальную часть характеристических показателей, ответственных за скорость ухода неустойчивых ионов из канала квадруполя. Когда фрагмент магнитного поля короткий и занимает несколько периодов ВЧ-поля, то происходит некоторая трансформация фазового объема, может быть даже и значительная, если индукция B0 велика, так что даже на короткой длине d успевают произойти большие вариации параметров движения, включающие и дисперсионные эффекты относительно массы m. Здесь можно предположить, что способ влияния на работу квадруполя существенно зависит от положения линзы, т. е. от параметра z, длины d — zx - z2 и величины безразмерного параметра магнитного поля λ. И здесь сценарий трансформации фазового объема может быть условно разбит на три типа.

I тип. Магнитная линза расположена в самом начале канала ( z 1 = 0) и преобразует фазовый объем ионного источника в некоторый новый, с которым и предстоит работать длинной части безмаг-нитного квадруполя. Магнитная линза производит своеобразную предварительную селекцию ионов по массам, которая заключается не обязательно в непосредственном выкидывании ионов еще в пределах линзы на стенки канала, а в подготовке благоприятной ситуации, каковая приведет к быстрому уходу нестабильных ионов в области квадруполя, свободной от магнитного поля.

II тип. Магнитная линза помещена в средней части канала. Фрагмент безмагнитного квадруполя уже успел деформировать начальный стартовый фазовый объем до некоторого состояния, и уже с этим объемом начинает работать магнитная линза. Она доводит его до нового состояния, и результат будет существенно иным, чем для сценария типа I. Далее с полученным фазовым объемом предстоит разбираться оставшейся части безмагнитного квадруполя. Приведет ли это к улучшению пропускания и разрешения, заранее сказать невозможно, ибо слишком сложна механика всего этого дела.

III тип. Магнитная линза расположена в конце канала у детектора. Разделение по массам уже произошло по классическому сюжету квадрупольного безмагнитного масс-анализа. При подходящих параметрах концевая линза может несколько увеличить разрешение, но еще вероятней, что она может выбросить полезные, уже отселектирован-ные ионы на стенки канала.

Теперь займемся аналитической стороной дела в некоторых предельных случаях, которые представляют собой своеобразную аналогию с электронной оптикой тонких линз, но совершенно с другим подходом. Мы рассмотрим очень узкие фрагменты d магнитного поля, в пределах которых вдоль z ионы летят малую долю периода ВЧ-поля, так что основным действующим фактором является закручивание ионов в поперечной плоскости xy. Эффект от этого закручивания нам заранее неиз- вестен. Чтобы рассмотреть такое локальное закручивание аналитическим образом, мы должны ввести своеобразную идеальную конструкцию в виде бесконечно узкого слоя d однородного магнитного поля с бесконечно нарастающей индукцией B0 ^ да, так что растет и X, но таким образом, что произведение оставалось постоянной величиной

Id = Q = const.                    (9)

Прохождение через такой слой мы назовем магнитным ударом.

МАГНИТНЫЙ УДАР

Выпишем сначала уравнения движения иона в продольном магнитном поле в безразмерной форме

' х = - [ ц + vf (т )] х + Лу ,

‘ y = ^[ ц ^{+ v f ( т )]} у ^{- Л х} ,                (10)

.z = zfr -т0) + z0, f (т +1) = f (т).

Начальные данные в поперечной плоскости запишутся в виде х|т=т 0 = х0,    УТ=т 0 = У 0, х1г=т 0 = х0,    Н=т 0 = степеням Δ, и их нам более чем достаточно для оценки реальной ситуации с очень короткими линзами. Подстановка данных (11) в (14) и (15) дает для x(τ), y(τ) следующие выражения х = х 0 + х0 • А +

+ "^{- ( ц + v cos2 nT ₀ ) х ₀ + Л - у ₀ } • А ² +

+ -^{2 nv sin2 nT ₀ • х ₀ - ( ц + v cos2 nT ₀ ) х ₀ +

+ Л [ ( ц + v cos2 nT ₀ ) у ₀ - Лх₀ ] } • А ³ + ...

у = у 0 ^{+ у} 0 ^^{А +}

+ ™{ ( ц + v cos2 nT ₀ ) у ₀ - Л ^ ,х ₀ } • А ² +

+ -^{- 2nv sin2 nT ₀ • у ₀ + ( ц + v cos2 nT ₀ ) у ₀ -

- Л [- ( ц + v cos2 nT ₀ ) х ₀ - Лу₀ ] } ^А ³ + ...

Дифференцируя эти выражения по А , получим скорости

.х = ,х ₀ + { - ( ц + v cos2 nT ₀ ) х ₀ + Л ^ у ₀ } • А +

+

{ 2 nv sin2 nT ₀

• х ₀ - ( ц + v cos 2 пт ₀ ) , х ₀ +

Нам надо проинтегрировать уравнения (10) на очень малом интервале времени Δ, пока частица не проткнет слой магнитного поля толщины d . Это время, очевидно, исчисляется величиной

+ Л [ ( ц + v cos2 nT ₀ ) у ₀ - Лх₀ ] } ^А ² + ... у = у ₀ + { ( ц + v cos 2 пт ₀ ) у ₀ - Л • ,х ₀ } • А +

А = — z0

.

+ —

{ - 2 nv sin 2пт ₀ • у ₀ + ( ц + v cos 2 пт ₀ ) у ₀

-

- Л [- ( ц + v cos2 nT ₀ ) х ₀ - Лу ₀ ] } -А ² + ...

Самое разумное здесь в условиях малости величины Δ разложить искомые решения x(τ), y(τ) в ряды Тейлора по степеням Δ. Для определенности положим f =cos2пт .

Тогда имеем из (10):

х = - [ ц + v cos 2 пт ] х + Лу , у = [ ц + v cos 2пт ] у - Лх.

Дифференцируя (14) по τ, запишем х = 2nv sin 2пт • х - [ ц + v cos 2пт] х + Лу, у = -2nv sin 2пт • у + [ц + v cos 2пт]у - Лх.

Этих данных вкупе с (11) вполне достаточно, чтобы расcчитать коэффициенты Тейлора и построить кубические отрезки рядов для решений по

По этим выражения можно сосчитать все необходимое при вполне конкретных А , например при А = 0.01 и любых Л разумных величин. Но нас будут интересовать очень большие λ (за счет больших В 0 ) и очень малые d .

Имеем

Л ^ d = Q = ХZ ₀ •А .                 (18)

Отсюда

Л ^А = Q .                     (19)

z ₀

При d ^ 0, А ^ 0, но с темпом, зависящим от z0. Если воспользуемся (19), подставим в (16) и (17) и далее устремим d ^ 0, А ^ 0 одновременно увеличивая λ, то в пределе для бесконечно узкого, но очень интенсивного магнитного поля получим следующие предельные формулы:

Положим о — x + i у и объединим (23) в комплексную форму

x ^ X 0 , У ^ У 0 ,              (20)

о —- i Лео .                    (24)

x ^ xо + yо • — --xо z0   2

Q 1

^y ^ У 0 + ^x 0 •---T У 0

z ₀   2

f Q У

У z 0 )

[ QI

У z 0)

= ^x k ,

= Ук .

Этот результат можно сформулировать в виде леммы.

Лемма

"За время прохождения через очень тонкий слой интенсивного продольного магнитного поля ион не успевает сместиться в поперечной плоскости, но вектор скорости ( x, У ) испытывает значительный поворот, не меняясь по величине. Этот поворот зависит от параметра Q и начальной скор^ости ( ^x 0 , ^у 0 , ^z 0 ) ".

Заметим, что электрическая сила при конечных µ и ν никак не отразилась на параметрах поворота при d ^ 0. Можно ли считать наши построения безупречными с математической и физической точек зрения? Сосчитаем величину ( x к + у к ) . Из (21) легко найти

¹ Q I

X k + У к = X 0 + У 0 +- — I ( X 0 + У 0 ) + ...

⁴ У z 0 )

Появился дополнительный член ~ Q ⁴ . Вывод можно сделать такой: последовательное многократное дифференцирование системы (14) нельзя ограничить конечным числом шагов, поскольку постепенно наращиваются члены вида ( Л -A ) n , n — 1,2,3,4..., которые дают добавки в предельные формулы (21). Следовательно, эти формулы справедливы только в условиях достаточно малых величин Q[z₀ , так что можно пренебречь старшими степенями. Здесь можно рассуждать следующим образом.

Коль скоро электрическое поле при конечных µ , ν не проявляется в предельных формулах, то имеет смысл сразу же его отбросить и оставить только магнитное поле. Система (10) при этом вырождается

x — Л- У, У — -Л - x.

Начальные данные тоже приведем к комплексной форме

^о Ь _т = ^x 0 ⁺ i У 0 = ° C

^{1 т —т} 0

° Т =_т = ^x 0 ⁺ i ^У 0 = ^о 0 .

Интегрируем (24) с учетом данных (25), получим уравнение вида

О = - i Ло + о ₀ + i Ло ₀.

Теперь напишем очевидное общее решение

о = Се

-1

^{i Лт} + о + ° ° .

⁰ i λ

Начальные условия дают уравнение для С :

•

о₀ = Се -'^{Лт 0}

ω

⁰ + о ₀ + —°

i λ

и

с = - °L е ^Лт 0 i λ

Окончательно:

.

•

„ _    ^О 0 ^- i ^{Л ( т - т} 0 )

о —--е iλ

ω ₀

⁺ ®0 ⁺~ . i λ

Для комплексной скорости дифференцированием получим выражение

о — о ₀

е ^{- i Л} ( ^т - г 0 )

Если теперь положить т - т ₀ — A , то из (30) и (31) имеем

ωk

ωk

о 0 _е-,Л А i λ

^{— о} 0

- i Л A e

ω ₀

+ о0 + т—, iλ

Если взять Л -А из (19) и устремить Л ^-да , а d ^ 0, то при заданной величине Q имеем

ок —

ω

⁺ о 0 ⁺ -f, i λ

- i Q

•            • Za ок — о0 е 0

Теперь получим точные формулы для тонкого слоя интенсивного магнитного поля. С ростом λ

ю_к ^ < у ₀ , т. е. частица не успевает сместиться |<у_к | = |< У 0|. Модуль скорости сохраняется, но сама она испытывает поворот. Приведем второе уравнение (33) к вещественной форме:

•             •           • •           / •           • • \

® k = x k + i У к = ( x 0 + i У 0 ) '

cos — - isin Q

V      z 0           z 0.

или

QQ x_k = x o COS — + y 0 sin—,

z ₀

Q

У к = У о cos— z ₀

-

z ₀

x _n sin Q .

z ₀

Рассчитанная своеобразная A -трансформация направления вектора скорости по существу дает обмен энергий между плоскостями xy и yz , а это может привести к самым неожиданным последствиям. Величина Q в действительности зависит от массы иона, если вспомнить, что λ пропорционально B 0 и обратно пропорционально массе m

X = qTB.(36)

m

Если положить

Bо • d = P,(37)

то с помощью (18), (36) и (37) получим связь

— = qTBоd = qTp .(38)

mm

Р назовем эффективностью магнитного слоя. Увеличивая B0 и уменьшая d так, чтобы Р сохранялось, мы теперь из (35) в пределе можем написать те же формулы (35), которые на самом деле годятся для любого слоя d. Если нет электрических полей, при наличии ВЧ-поля лучше их рассматривать как предельные для очень тонкого магнитного слоя. Подставим (38) в (35) и запишем qT         qT xk = x 0cos----P + У 0 sin mz0mz qTqT

Ук = У0 cos—P - xi:sm mz0

При заданной эффективности Р очень короткой магнитной линзы мы видим, что более легкие ионы испытывают больший поворот и имеет место своеобразная угловая дисперсия по массам, которая потом может реализоваться в безмагнитной части квадрупольного канала некой дополнительной линейной дисперсией по массам.

Если такая линза расположена в начале канала, то за счет дополнительного поворота ионов может оказаться, что именно та часть, которую мы в данный момент проводим к детектору, оказывается в оптимальном овале, а прочие массы в него не попадают и хотя бы частично отсекаются.

Когда линза такова, что A содержит 1, 2, 3 или более периодов ВЧ-поля, то механизм поворота существенно искажается электрическим взаимодействием, при котором меняется модуль скорости | <у |, а это в свою очередь приводит к дополнительным поворотам за счет магнитного поля, если | <у | растет, и, наоборот, ионы не докручиваются, если скорость |< у | падает. Все это приводит к интереснейшей игре факторов, которые отличают эту ситуацию от той, что реализуется при приложении продольных магнитных полей вдоль всего канала.

В случае реальной магнитной линзы с колоколообразным ходом напряженности вдоль оси z движение ионов, безусловно, осложняется, но мы вправе предполагать, что главные черты явлений сохраняются, как это имеет место и в статической "магнитной" электронной оптике при переходе от идеальных моделей линз к реальным. В заключение отметим, что разрывные модели магнитного поля следует рассматривать как вариант сильно неоднородных полей, что может быть полезным в дальнейших исследованиях.

МОДЕЛИРОВАНИЕ ФИЗИЧЕСКОГО ЭКСПЕРИМЕНТА

Для подкрепления проведенных аналитических оценок было проведено масштабное моделирование физического эксперимента: совмещался классический квадруполь и короткая магнитная линза как небольшой сегмент продольного однородного магнитного поля, последняя размещалась в разных точках канала. Вычислялась функция пропускания масс-фильтра как количество прошедших ионов в некотором диапазоне масс к общему числу частиц, влетающих в канал квадруполя, при этом условия ввода ионов в масс-фильтр задавались в некоторых пределах, диктуемых размером канала. Для удобства протяженность сегмента магнитного поля определялась целым числом периодов колебания ВЧ-составляющей электрического питания. Магнитное поле начинает воздействовать на частицы в один и тот же момент времени, но ионы, попадающие в канал с разными начальными условиями — углами влета, — будут находиться в разных поперечных плоскостях канала, т. е. граница магнитного поля будет не плоской, а искривленной (за исключением крайних положений сегмента магнитного поля — в начале канала и в конце).

Такой подход отражает реальные условия, поскольку даже при использовании постоянных магнитов определенной длины границы магнитного поля, проникающего в канал, размыты.

Частицы влетают в область поля в разные фазы колебаний электрической составляющей, однако для проведения оценки воздействия магнитного поля мы ограничились условием, что ионы попадают в канал в нулевую фазу.

Было рассмотрено три режима, когда площадь магнитного удара сохраняется, т. е. действует условие (9). В терминах величин индукции магнитного поля b 3 и длительности по времени А :

• 1)    b 3 = 0.4, T = 4∙2 π ,

• 2)    b 3 = 0.8, T = 2∙2 π , (40) 3) b 3 = 0.2, T = 8∙2 π .

На рис. 1 представлены кривые пропускания этих режимов, когда магнитная линза устанавливается в начале канала.

Наиболее оптимальным оказывается режим первый. При малой величине магнитного поля (вариант 3) воздействие слабое, т. к. мало отличается от функции пропускания классического квадруполя. Для классического квадруполя характерная функция пропускания представляет собой широкую полосу с почти вертикальными фронтами, с одной стороны — соответствующий точке λ = = 0.64, а с другой — точке λ = 0.72. Высота функции составляла максимальную величину, равную 1. Вариант 2 — магнитное поле подавляет в целом возможность какой-либо селекции в канале. Режим 1 был взят за основу в дальнейших численных экспериментах.

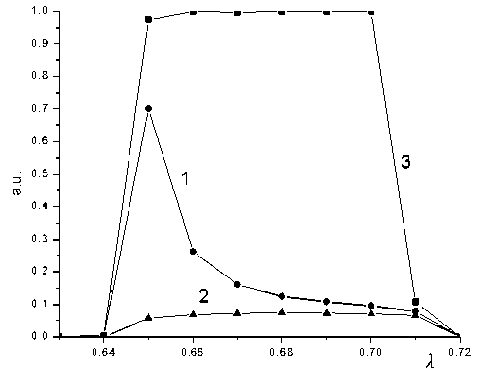
Рис. 1. Функция пропускания для квадруполя с продольным магнитным полем в виде небольшого сегмента, установленного в начале канала, для трeх режимов работы (40)

Результаты моделирования при смене положения магнитной линзы вдоль канала представлены на рис. 2. Для удобства проведения численного эксперимента точка установки линзы определялась кратно длине самого сегмента, т. е. 8 π (в единицах периода колебаний ВЧ-составляющей питания). Таким образом, возможных положений сегмента составляет 12. Цифра, указывающая номер графика (1–11), также отражает протяженность безмагнитной части канала квадруполя, предшествующей магнитному сегменту. Последний вариант 12 иллюстрирует ситуацию, когда магнитное поле включается в последние периоды ВЧ-колебаний.

Как видно, нельзя отдать преимущество какому-либо варианту: все имеют значительный всплеск в начале массового диапазона, т. е. преимущественно отбираются легкие ионы. Интенсивность сигнала выше в случае, когда сегмент располагается в первой половине канала. Шлейф представляет собой частокол, форма которого меняется от точки расположения сегмента магнитного поля. Лишь последний вариант, когда сегмент магнитного поля установлен в конце канала, выбивается из этой плеяды: происходит подавление сигнала в целом, интенсивность сильно падает.

О ФРАГМЕНТАХ ПОПЕРЕЧНОГО К ОСИ КВАДРУПОЛЯ ОДНОРОДНОГО МАГНИТНОГО ПОЛЯ

Теперь мы должны разобраться с действием однородного магнитного поля, поперечного к оси z и действующего, например, в направлении оси x . Если вырезать фрагмент такого магнитного поля и двигать его по оси z , то обнаружатся новые явления здесь, как и в случае с однородным магнитным полем вдоль оси z . Как и в том случае, тоже можно рассмотреть предельно узкий фрагмент высокой интенсивности, с тем чтобы "распутаться" с влиянием электрического поля.

Положим

Ь 1 = 1, ь 2 = ь 3 = о                    (41)

и запишем уравнения движения в отсутствие электрического поля ц = v = 0 :

[ x - О,

• • У = Az,                      (42)

z = - Ху.

Эта система отличается от (23) только циклической заменой букв: x ^ у , у ^ z , z ^ x . Формулы поворота вектора скорости будут точно такими же, как и (39), только с переменой символов. Физически поворот происходит в плоскости yz , и это,

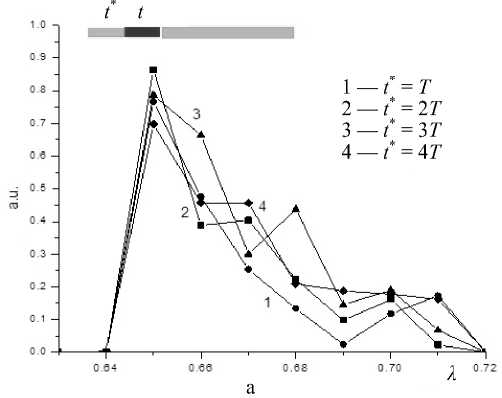
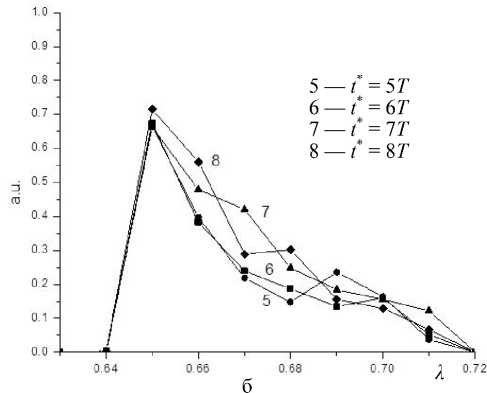
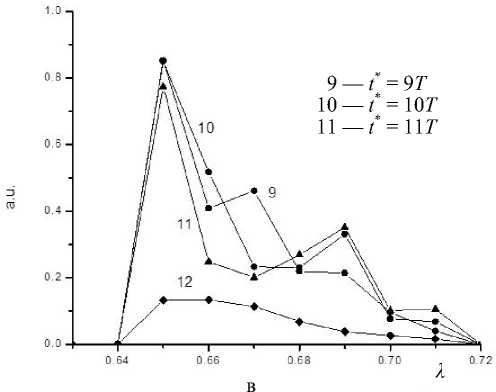
Рис. 2. Функция пропускания для квадруполя с продольным магнитным полем в виде небольшого сегмента, расположенного в разных точках канала.

а — функции 1–4, б — 5–8, в — 9–11. Номер кривой (1–11) определяет положение сегмента по отношению к началу канала масс-фильтра. Функция пропускания 12 отвечает положению сегмента в конце канала конечно, фатально отличает ситуацию от продольного поля. Действительно, вдоль оси x без электрического поля ион дрейфует, а в плоскости yz резко вращается. Если первоначальный импульс иона был вдоль оси z, то после воздействия магнитного слоя он будет направлен вдоль оси y, и частицу может выкинуть на границу. Когда ц * 0, v * 0, уравнения движения будут x = -[ Ц + vf (т )] x,

‘ y = [ Ц + ^{v f ( т} ) ] У + /-z             ⁽⁴³⁾

z = - Лу.

Интегрируя третье уравнение из (43), получим z = c - Лу .                        (44)

Вставляя (44) в (43), получим y = [ц - Л2 + wf(т)]у + Xc. (45)

Получилась ситуация со сдвигом границы зоны по µ по сравнению с классическим безмагнитным квадруполем. Поэтому толстый слой поперечного магнитного поля в присутствии ВЧ-поля может вести себя весьма прихотливо в зависимости от его параметров и еще от z₀ , поскольку С зависит от z₀ . Если менять направление поля на противоположное, т. е. менять знак λ , то сдвиг зон будет таким же, т. к. λ в (45) при y входит как λ ² , но постоянная сила λс меняет знак.

Это наблюдение приводит нас к интересной мысли. Если вдоль z выстроить ряд параллельных одинаковых фрагментов магнитного поля, но с переменой знака В0 при переходе от одного к другому, то получится весьма новая физическая обстановка для ионов, в которой могут наблюдаться некие резонансные явления, порожденные пространственной периодичностью магнитного поля и временнóй периодичностью электрического поля. Один фрагмент может оказаться губительным для пропускания, но множество их может в корне поменять сценарий фильтрации по оси z. В заключение еще подчеркнем, что такой вариант магнитных полей совершенно не затрагивает проекцию траекторий на ось х. Там действует прежняя классика, но в плоскости yz могут проявиться необыкновенные эффекты.

Таким образом, проведенный анализ и моделирование показали, что даже небольшой фрагмент магнитного поля вносит дополнительную селективность в ионных потоках, пропускаемых через классический квадрупольный масс-спектрометр. В некоторых экспериментальных условиях такая ситуация оказывается более выгодной по сравнению с вариантом однородного магнитного поля, протяженного вдоль всего канала масс-фильтра. При приложении короткой магнитной линзы удается повысить разрешающую способность на порядок и более, а также увеличить и чувствительность прибора.