Влияние механической нагрузки на результирующие пьезомодули композита
Автор: Паньков А.А.
Статья в выпуске: 3, 2022 года.
Бесплатный доступ
Разработана математическая модель и на ее основе найдены аналитические решения для результирующих «редуцированных» электроупругих характеристик, в частности: деформационных (сдвиговых) пьезомодулей и диэлектрических проницаемостей трансверсально-изотропного пьезоэлектрического материала (композита) с учетом поправок, обусловленных наличием механических осевых напряжений и электродеформационной переориентации оси симметрии свойств материала при действии электрического поля. В начальной конфигурации осевые растягивающие и / или сжимающие напряжения не приводят к появлению сдвиговых деформаций материала, сдвиги инициируются приложением электрического поля и «усиливаются» осевыми напряжениями начальной конфигурации. Выявлен эффект увеличения результирующих значений деформационных пьезомодулей материала от действия осевых напряжений. Величины приложенных осевых напряжений не превышают значений потери устойчивости материала (элементов структуры и в целом композита), что обусловливает сохранение эффекта увеличения пьезомодулей также при действии переменного электрического поля. Результаты численного моделирования получены для трансверсально-изотропного полимерного композита «силикон/PZT-4» с однонаправленными пьезоэлектрическими волокнами с круглым поперечным сечением как частного (предельного) случая структуры с ориентированными эллипсоидальными включениями с использованием известного «обобщенного сингулярного приближения» на основе метода функций Грина статистической механики композитов для вычисления тензоров эффективных свойств композита в текущей конфигурации. Поправки деформационной анизотропии вычисляются через текущие координаты направляющего вектора для оси симметрии свойств - направления ориентации волокон композита. Установлено, что наиболее значительно эффект увеличения сдвиговых пьезомодулей проявляется для однонаправленного волокнистого композита с низкомодульной полимерной матрицей «силикон/PZT-4» при малых значениях объемной доли жестких пьезоэлектрических волокон от действия сжимающего продольного осевого напряжения.
Композит, эффективные свойства, пьезоэффект, переориентация волокон, численное моделирование
Короткий адрес: https://sciup.org/146282552
IDR: 146282552 | УДК: 539.3 | DOI: 10.15593/perm.mech/2022.3.07
Текст научной статьи Влияние механической нагрузки на результирующие пьезомодули композита
ВЕСТНИК ПНИПУ. МЕХАНИКА № 3, 2022PNRPU MECHANICS BULLETIN
Нелинейные эффекты деформирования полимерных композиционных материалов обусловливаются различными факторами, в том числе наличием начального напряженного состояния [1–3] на различных структурных уровнях и / или взаимовлиянием различных типов нагрузок при комбинированном нагружении [4; 5] материала. Так, в [5] выявлено влияние дополнительных крутильных вибраций различной частоты на диаграммы одноосного квазистатического растяжения углепластиковых трубчатых образцов. Изучение закономерностей и эффектов влияния начального, в том числе остаточного, напряженного состояния элементов структуры композиционного материала на особенности его последующего деформирования с редуцированием эффективных свойств актуально для различных приложений механики композитов [6–13], в частности, ультразвукового неразрушающего контроля напряженного состояния нагруженных конструкций [12], методов геомеханики и сейсмических исследований [13]. Математическое моделирование и решение таких задач основывается на линеаризованных моделях, которые используют описание напряженно-деформированного состояния посредством, в частности, тензоров механических напряжений в начальной и текущей конфигурациях [3; 8; 9; 14; 15–28]. Линеаризованная модель использована в [21], где изучены теоретические аспекты идентификации неоднородного начального напряженного состояния упругих тел по собственным час- тотным спектрам как решений обратных задач механики стержней и тонких пластин. Дисперсионный анализ распространения упругих волн в композиционных материалах и элементах конструкций с учетом наличия начального напряженного состояния осуществлен в работах [22–28], в частности, исследованы скорости распространения поверхностных волн в однородном слое на предварительно напряженном неоднородном полупространстве [22], влияние величины начального бокового давления на поверхности полого составного цилиндра на скорость распространения осесимметричной волны [23], влияние величины начального напряженного состояния ортотропной композитной пластины с двумя близко расположенными параллельными цилиндрическими (туннельными) полостями с прямоугольным поперечным сечением на свободные и вынужденные колебания [24]. Для упругих композитов с идеально периодическими начально-напряженными структурами известны асимптотические решения в [25–28], в частности, когда начальное напряженное состояние слоистой и однонаправленно-волокнистой структур композитов обусловлено их тепловым нагревом [25]. Изучение эффектов влияния начального напряженного состояния на свойства и поведение материала актуально также для пьезоэлектрических [29–34] и / или магнитострикционных [35] материалов [36–38], которые интегрируются в современные «интеллектуальные» конструкции в качестве информационных элементов, датчиков и / или актюаторов систем управления акустическими и / или аэродинамическими характеристиками поверхностей, геометрической формой, напряженным состоянием, демпфированием вибраций конструкции [33; 39]. Численный анализ динамического поведения пьезоэлектрических структур с учетом начального электромеханического напряженного состояния элементов структуры дан в статье [31]. Эффект увеличения пьезоэлектрических модулей предварительно напряженных пластинчатых пьезоэлектрических элементов исследован в [32–34]. Повышение пьезочувствительности биморфа в составе конструкции, когда биморф закрепляют на обшивке аэродинамического профиля лопасти осуществляется в работе [33] посредством начального сжатия гибкой подложки. Линеаризованный подход обобщен на электроупругий материал в [29; 30], где дано описание линеаризованной модели, учитывающей в явном виде начальные механические напряжения, деформации и напряженность электрического поля. Обобщение на маг-нитоэлектроупругий материал дано в работе [35], где изучены дисперсионные соотношения для упругих волн в слоистом композите – фононном кристалле, образованном периодическим повторением предварительно напряженных пьезоэлектрических и магнитострикционных слоев.
Цель настоящей работы состоит в нахождении аналитических решений для результирующих «редуцированных» значений электроупругих характеристик трансверсально-изотропного пьезоэлектрического материала (композита) с учетом поправок, обусловленных наличием механических осевых напряжений и электродефор-мационной переориентации оси симметрии свойств материала при действии электрического поля. В начальной конфигурации осевые растягивающими и / или сжимающими напряжениями не приводят к появлению сдвиговых деформаций материала, сдвиги инициируются приложением электрического поля и «усиливаются» осевыми напряжениями начальной конфигурации. Величины приложенных осевых напряжений не превышают значений потери устойчивости материала (элементов структуры и в целом композита), что обусловливает возвращение оси симметрии из текущей «повернутой» ориентации в первоначальную при снятии (выключении) электрического поля и сохранение эффекта усиления результирующих деформационных пьезомодулей материала также при действии переменного электрического поля. При численном моделировании электромеханического нагружения полимерного композита «силикон/PZT-4» с эллипсоидальными включениями (волокнами) поправки деформационной анизотропии вычисляются через текущие координаты направляющего вектора для оси симметрии материала, что трактуется как изменение общей ориентации (или преобладающей ориентации для случая стохастического взаимного разориентирования продольных осей) однотипных эллипсоидальных включений, в частности волокон с круглым поперечным сечением. Использованы известные численно-аналитические решения обобщенного сингулярного приближения, основанные на методе функций Грина статистической механики композитов, для вычисления тензоров эффективных свойств материала в текущей конфигурации.
1. Математическая модель деформационного редуцирования электроупругих свойств материала
Рассмотрим математическую модель электроупруго-го поведения трансверсально-изотропного пьезоэлектрического материала (композита) с учетом поправок для материальных характеристик от наведенной электрическим полем «деформационной анизотропии» – изменения ориентации оси симметрии свойств материала, когда r1r2 – плоскость изотропии, r3 – ось симметрии для начальной конфигурации. Считаем, что механическое нагружение σ0 материала осуществляется осевыми напряжениями σ101 , σ022 , σ303 вдоль главных осей r1,2,3 (остальные компоненты σi0j = 0), при которых сдвиговые деформации γ 023 = γ 103 = γ102 = 0 для начальной конфи- гурации материала. Сдвиговые деформации γ13 , γ23 возникают лишь под действием напряженности E электрического поля у13 = 2dn 13ЕВn, у23 = 2dn23En , что обусловливает переориентацию оси симметрии свойств материала по направляющему вектору
l ={γ13,γ23,1} (1)
с координатами l i в осях координат r 1,2,3 с учетом малости углов сдвига γ и, как следствие, приближенных равенств cos γ≈ 1 , sin γ≈γ , где dn 13 , dn 23 – деформационные (сдвиговые) пьезомодули материала [36] в начальной конфигурации.
Определяющие соотношения [36] для электроупру-гого материала запишем в виде
^ = Sjmn - + dn^n , D = firn^L +^ fiEn ,(2)
'
где «редуцированные» компоненты ε ij , D i тензора деформаций ε ' и вектора индукции D ' выражены через
0 В компоненты σmn , En тензора напряжений σ и вектора напряженности E электрического поля. Редуцированные компоненты тензоров эффективных упругих податливостей Si'jmn (γ) , деформационных пьезомодулей dimn ( γ ) и диэлектрических проницаемостей λi(nσ) (γ) материала (2) в начальной системе координат r1,2,3 являются функциями текущих сдвиговых деформаций γ = {γ13, γ23}, что обусловлено зависимостью от γ значений координат li направляющего вектора l (1)
для оси симметрии свойств материала. Компоненты тензоров Si ' jmn , di ' mn и λ ' i ( n σ ) (2) в начальной системе координат r 1,2,3 представим разложениями по тензорным базисам [42]
Sijmn = s 12 δ ij δ mn + s 66( δ im δ jn +δ in δ jm ) +
+ ( s 11 + s 33 - 2 s 13 - 4 s 44) liljlmln + ( s 13 - s 12)( lilj δ mn +δ ijlmln ) +
+ ( s - s )( δ ll +δ ll +δ ll +δ ll ) (3)
44 66 jnim im j n jm i n in j m , di'mn=d31liδmn+(d33-d31-2d15)lilmln+d15(lmδin+lnδim),
λ'(σ) =λ(σ)δ+(λ(σ)-λ(σ))ll , in 1in 31i n где δ – символ Кронекера, матричные обозначения s11 = S1111 , s33 = S3333 , …, d31 = d311 , d33 = d333 , d15 = d113 , λ1(σ) = λ1(1σ), λ3(σ) = λ3(σ3) для компонентов тензоров S , d , '(σ)
λ в осях r 1,2,3 .
Таким образом, редуцирование значений компонентов тензоров эффективных упругих податливостей S i ' jmn , деформационных пьезомодулей d i * mn и диэлек- '( σ )
трических проницаемостей λ in материала в начальной системе координат r 1,2,3 происходит по линейным зависимостям
S ' = S +κ E d ' = d +χ E ijmn ijmn pijmn p , imn imn ipmn p ,
X\a)=x(t)+c (4)
ik ik ςpik p от величины напряженности E электрического поля с учетом имеющихся пропорциональных зависимостей координат li (1) направляющего вектора l от γ , γ от E и пренебрежимой малости величин γ2 ≈0 для углов сдвига γ, где первые слагаемые Sijmn , dimn λi(nσ) – компоненты тензоров электроупругих свойств материала (композита) для случая E = 0 (т.е. при l r3 ) могут быть рассчитаны, например, методами статистической механики композитов [37; 38; 40; 41], коэффициенты пропорциональности κ , χ , ς – искомые характеристики материала.
В результате подстановки разложений (4) в (2) получим (для рассматриваемого случая нагружения σ 0 , E материала) уточненные соотношения
£-= S-- о + d • E ,6=d- C70 + X(a> E (5)
ij ijmn mn nij n , iimnmninn в линейном приближении, отбрасывая квадратичные слагаемые по переменным Ei , где dn•ij , λi(nσ)• – компоненты тензоров результирующих значений деформационных пьезомодулей d• и диэлектрических проницае-мостей λ(σ)• имеют вид d• =d+κ σ0 , λ(σ)•=λ(σ)+χσ0
pij pij pijmn mn , ip ip ipmn mn
с учетом (2), (4), (5). Коэффициенты пропорциональности κ pijmn , χ ipmn (4), (6) могут быть найдены как производные
К - pijmn
∂ S ' ijmn
.*.
∂ E p
∂ d ' imn
X iPmn дE ’
или в результате нахождения вида явных линейных зависимостей величин Si ' jmn , d i ' mn от напряженностей E p (4) с учетом разложений (3) и пренебрежимой малости величин γ 2 ≈ 0 . Для этого выражения (3) для компонент S i ' jmn , d i ' mn преобразуем к виду
Si ' jmn = Sijmn + ( s 11 + s 33 - 2 s 13 -4 s 44)∆ ijmn +
+(s„-s„)(A 5 + 5-A ) + 13 12 ij mn ij mn
A +5. A. +5. A. +5. A. (8) 44 66 jnim im jn jmin in jm, di'mn = dimn + d31∆iδmn +(d33 -d31 -2d15)∆imn +
+ A- =11 I 5. , A- =111 l Д 5. , imn i m n 3i 3m 3n , ijmn i j m n 3i 3j 3m 3n , которые имеют лишь следующие ненулевые значения: ∆1=l1, ∆2=l2, ∆13 =∆31 =l1 , ∆23 =∆32 =l2 , ∆133 = ∆313 = ∆331 =l1 , ∆233 = ∆323 = ∆332 =l2 , ∆1333 = ∆3133 = ∆3313 = ∆3331 =l1 , ∆2333 = ∆3233 = ∆3323 = ∆3332 =l2 и допускают запись в виде ∆i=l1δ1i+l2δ2i, ∆ij=l1(δ1iδ3j+δ3iδ1j)+l2(δ2iδ3j+δ3iδ2j), А. =/,(5, Д 5. +5. 5, 5, +5,5, 5, ) + imn 11i 3m 3n 3i 1m 3n 3i 3m 1n +/,(5, 5, 5, +5, 5, 5, +5, 5, 5, ), 22i3m3n 3i2m3n 3i3m2n, ∆ijmn=l1(δ1iδ3jδ3mδ3n+δ3iδ1jδ3mδ3n+ +δ3iδ3jδ1mδ3n+δ3iδ3jδ3mδ1n)+ +l2(δ2iδ3jδ3mδ3n+δ3iδ2jδ3mδ3n+δ3iδ3jδ2mδ3n+δ3iδ3jδ3mδ2n), где координаты направляющего вектора (1) rs l1=γ13=2dn13En, l2=γ23=2dn23En (10) имеют пропорциональные зависимости от напряженностей En электрического поля. Таким образом, после дифференцирования левых и правых частей равенств (8) для Si'jmn , dimn по переменной En получим искомые решения для коэффициентов пропорциональности κpijmn, χipmn (4)–(7) в виде материала) напряжений, где коэффициенты пропорциональности κ11333 , κ11311 и κ22333 , κ22311 находим из решений (11), (12) с учетом (4) пропорциональных зависимостей ' l ' l ' l S1333 = κ11333E1 , S1311 =κ11311E1 , S2333 = κ22333E2 , S2322 = κ22322E2 , κ pijmn ∂S' ijmn .*. ∂Ep =(s11+s33-2s13-4s44)∆ijmn,p+ +(^n-^n)(A з +3-А )+ (11) 13 12 ij,p mn ij mn,p “Ь^лл — - А- + 3- А. + 3. А- + 3- А. ), 4466jn im,p im jn ,p jm in,p in jm,p, χipmn ∂di'mn .*. ∂Ep = tLA. 5 + 31 i,p mn +(d„-d„-2d,M + б +А б), 33 31 15 imn, p 15 m,p in n,p im , где с учетом разложений (9) имеем следующие выражения для производных ∆i,p=2dp13δ1i+2dp23δ2i, ∆ij,p=2dp13(δ1iδ3j+δ3iδ1j)+2dp23(δ2iδ3j+δ3iδ2j), ∆imn,p=2dp13(δ1iδ3mδ3n+δ3iδ1mδ3n+δ3iδ3mδ1n)+ +2dp23(δ2iδ3mδ3n+δ3iδ2mδ3n+δ3iδ3mδ2n), (12) ∆ijmn,p=2dp13(δ1iδ3jδ3mδ3n+δ3iδ1jδ3mδ3n+ +δ3iδ3jδ1mδ3n+δ3iδ3jδ3mδ1n)+ p23 2i3j3m3n 3i2 j3m3n 3i3j2m3n +ДДД б, ) 3i3j3m2n с учетом вида производных 8L дEE п 13 np p 13, дjE n23^np p23 для величин l1= 2dn13En, l2= 2dn23En, ^l дЕ=б ∂Ep np Так как ненулевыми компонентами тензора σ0в осях r1,2,3 00 0 являются лишь осевые напряжения σ101 , σ022 , σ303 , по- этому из формул (6) следуют решения, в частности, для результирующих деформационных пьезомодулей d113 = d113 + κ11333σ33 +κ11311σ11, d223 = d223 + κ22333σ33 + κ22322σ22 как линейных функций «продольного» σ033 и «поперечных» σ101 , σ022 (относительно оси симметрии свойств выполняются равенства: S1333= S1311= S2333= S2322=0, d223= d113 , d223= d113 , κ22333= κ11333 , κ22322= κ11311 . Зависимости (14) обусловливают увеличение результирующих деформационных пьезомодулей d1•13 , d2•23 материала (композита) от действия продольной сжимающей σ303 00 и / или поперечных растягивающих σ11 , σ22 нагрузок. Композиционный материал. Для случая, когда рассматриваемый трансверсально-изотропный материал – двухфазный композит, например, с пьезоэлектрическими эллипсоидальными ( a1,2,3 ) ориентированными включениями (волокнами) в низкомодульной упругой матрице, тогда в полученных решениях (5), (6) обозначения ε', D', σ0, E соответствуют «макроскопическим», т.е. осредненным по представительной области V компози-'* _0* ir" та значениям тензоров ε , D , σ0, E , а величины S , d , λ(σ)– тензоры S*, d*, λ(σ)*эффективных трансверсально-изотропных электроупругих свойств композита могут быть рассчитаны, в частности, в обобщенном сингулярном приближении [38; 41; 43] на основе метода функций Грина G(r) для однородной трансверсальноизотропной пьезоэлектрической среды [43], где a1,2,3 – главные полуоси включений ( a2= a1). В представительной области V композита эллипсоидальные включения распределены по объему статистически однородно при относительном объемном содержании v1 . В начальной конфигурации продольная полуось a3 ориентирована вдоль оси r3 , параметр формы включений q= a1,2 / a3 равен 1 для сферических включений, q > 1 или q< 1 для «дисковых» или «игольчатых» включений, а для предельных случаев q →∞ или q → 0 для слоев или однонаправленных волокон с круглым поперечным сечением соответственно. Подход сводит задачу «эффективного модуля» статистической механики композитов к решению систем интегродифференциальных уравнений, ядра которых – вторые производные функций Грина ∇∇G(r), где ∇ – оператор дифференцирования по координатам r. В этом приближении у вторых произ- водных функций Грина ∇∇G(r) учитываются лишь сингулярные составляющие [43] ∇∇G(r-r1)≈Gsδ(r-r1), Gs Uismjn Φs imn s(1) imn Φs(1) mn с эллипсоидальным ( a1,2,3 ) «зерном неоднородности» – областью интегрирования малой окрестности точки сингулярности производных WG(r) [41; 43].
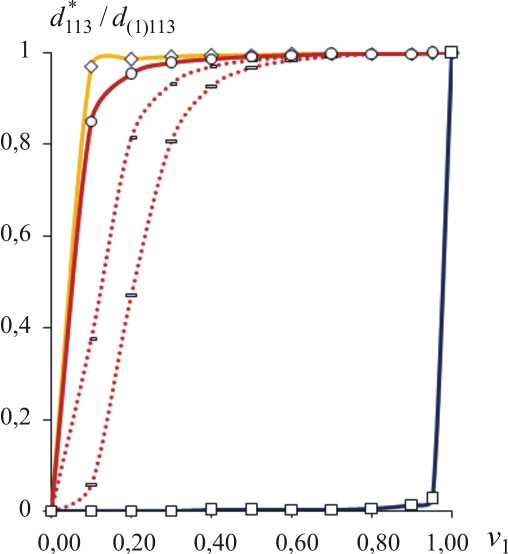
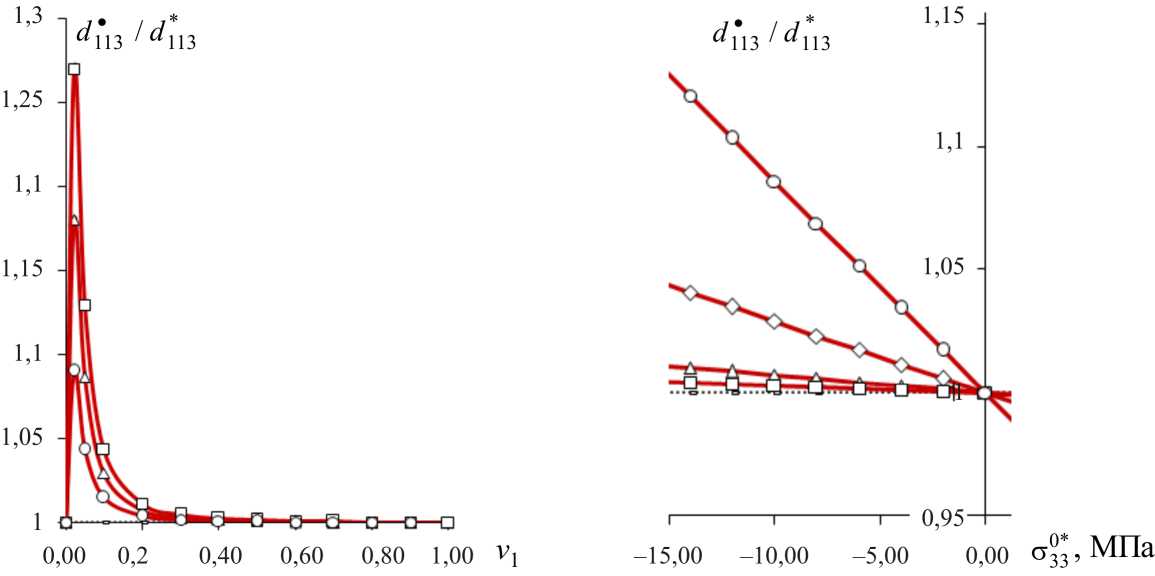
2. Результаты численного моделирования В качестве тестовой задачи на рис. 1 приведены результаты сравнения рассчитанных в обобщенном сингулярном приближении [38; 43] значений эффективного объемного пьезомодуля dv*однонаправленного волокнистого композита «эпоксид/PZT-4» с известными решениями (■) [44], (•) [45] для композита с периодической гексагональной укладкой цилиндрических пьезокерамических волокон PZT-4 в эпоксидной матрице с модулем Юнга Е(2) = 3 ГПа, коэффициентом Пуассона v(2) = 0,4, относительной диэлектрической проницаемостью X (2) / X 0 = 5. Здесь d(1)v - объемный пьезомодуль для 1-й фазы (PZT-4) с учетом выражения dv = dззз + 2dэн ■ Решение для d* [44] получено на основе стержневой модели [45] – с использованием быстрых переменных и асимптотических разложений в ряды. Рассмотрим численный анализ (13), (14) влияния продольной сжимающей σ30*3 нагрузки на результирующий деформационный пьезомодуль d 1*13 композита «силикон/PZT-4» с однонаправленными трансверсально-изотропными пьезоэлектрическими волокнами (PZT-4) [36] в изотропной упругой матрице (силикон) с модулем Юнга Е(2) = 0,1 ГПа, коэффициентом Пуассона v(2) = 0,3, относительной диэлектрической проницаемостью X(2) / X0 = 3. Для такого композита c низкомодульной упругой матрицей и при нагрузке σ03*3< 0 эффект увеличения величины d1*13 проявляется наиболее ярко. Результаты вычисления деформационного пьезомодуля d1*13 для композита «силикон/PZT-4» даны на рис. 2. Решение (○) соответствует традиционному сингулярному приближению [37; 40; 41], при котором тензоры электроупругих свойств Cc , ec , λc среды сравнения приравнены к осредненным по Фойгту или «правилу смеси» значениям, например, тензор упругих свойств Cc =< C >= v1C1 + (1 - v1)C2, где <...> - оператор осреднения по представительной области V композита. Решения (◊, □) соответствуют «вилке Хашина – Розена» для однонаправленного волокнистого композита, когда среда сравнения имеет свойства 1-й (◊) или 2-й (□) фазы композита соответственно. Пунктирные графики на рис. 2 построены для случаев, когда характеристики среды сравнения Cc , ec , λc заданы по правилу смеси, например, Cc = U1C1 + (1 - и1 )C2 с использованием приведенных степенных значений и1 = v 12(-), v 13(-) объемной Рис. 1. Эффективный объемный пьезомодуль dv* волокнистого пьезокомпозита со «средой сравнения» по Фойгту (○), по 1-й фазе (◊), по 2-й фазе (□) Рис. 2. Зависимости относительного эффективного деформационного пьезомодуля d1*13композита «силикон/PZT-4» от объемной доли v1 пьезоэлектрической 1-й фазы ( d(1)113) двухфазного композита со «средой сравнения» по Фойгту (○), по 1-й фазе (◊), по 2-й фазе (□) Fig. 1. Effective volumetric piezomodule dv*of fibrous piezocomposite with "comparison medium" by Foigt (○), by 1st phase (◊), by 2nd phase (□) Fig. 2. Dependence of relative effective deformation piezomodule d1*13 of "silikon/PZT-4" composite on volume fraction v1of piezoelectric 1st phase ( d(1)113) of two-phase composite with "comparison medium" by Foigt (○), by 1st phase (◊), by 2nd phase (□) Рис. 3. Зависимости относительного результирующего деформационного пьезомодуля d1•13композита «силикон/PZT-4» от объемной доли v1пьезоэлектрических волокон при нагрузке σ30*3= 0 ( ̶), – 5 (○), – 10 (Δ), – 15 (□) [МПа] (а) и от нагрузки σ30*3 при v1= 0,05 (○), 0.1 (◊), 0.2 (Δ), 0.3 (□), без учета переориентации волокон (пунктирная линия) (b) Fig. 3 Dependences of the relative resulting deformation piezomodule d1•13of a composite "silicone/PZT-4" from a volume fraction v1 of piezoelectric fibers at loading σ30*3= 0 ( ̶), – 5 (○), – 10 (Δ), – 15 (□) [MPa] (a) and from loading σ03*3at v1= 0.05 (○), 0.1 (◊), 0.2 (Δ), 0.3 (□), without reorientation of fibers (dotted line) (b) доли v1волокон [46]. Выявлен эффект увеличения результирующих модулей d1•13 , d2•23 (13), (14) композита «силикон/PZT-4» от действия продольной сжимающей 0* 0* 0* σ33 и поперечных растягивающих σ11, σ22нагрузок. В частности, для относительной величины d1•13/ d1*13 результирующего модуля d1•13 на рис. 3 построены графики немонотонных зависимостей d1•13 / d1*13 от объемной доли v1 пьезоэлектрических волокон (рис. 3, а) и линейных зависимостей d1•13 / d1*13 от продольного сжимающего напряжения σ03*3 (рис. 3, b). Заключение Разработана математическая модель и на ее основе найдены аналитические решения (5), (6), (11), (12) для результирующих «редуцированных» значений электро-упругих характеристик, в частности: деформационных (сдвиговых) пьезомодулей d• и диэлектрических прони-цаемостей λ(σ)• трансверсально-изотропного пьезоэлектрического материала (композита) с учетом поправок (6), обусловленных наличием механических осевых напряжений σ0 и электродеформационной переориентации оси симметрии свойств материала по направляющему вектору l (1) при действии электрического поля. Резуль- тирующие значения тензоров d• , λ(σ)• линейно зависят от действующих напряжений σ* (6) с коэффициентами пропорциональности κ , χ (11), (12). Выявлен эффект увеличения результирующих значений компонент d1•13 , d2•23 (14) деформационных пьезомодулей d• (6) материала от действия осевых напряжений σ0 . Величины приложенных осевых напряжений σ0 не превышают значений потери устойчивости материала (элементов структуры и в целом композита), что обусловливает сохранение эффекта увеличения величин d1•13 , d2•23 также при действии переменного электрического поля. Результаты численного моделирования (см. рис. 1–3) получены для трансверсально-изотропного полимерного композита с однонаправленными пьезоэлектрическими волокнами с использованием известного обобщенного сингулярного приближения [38; 43] на основе метода функций Грина (15) [43]. Установлено, что наиболее значительно эффект увеличения величины d1•13 / d1*13 от сжимающего напряжения σ03*3 проявляется для однонаправленного волокнистого композита с низкомодульной полимерной матрицей, например, «силикон/PZT-4» при малых значениях v1 < 0,2 объемной доли жестких пьезоэлектрических волокон (рис. 3, а).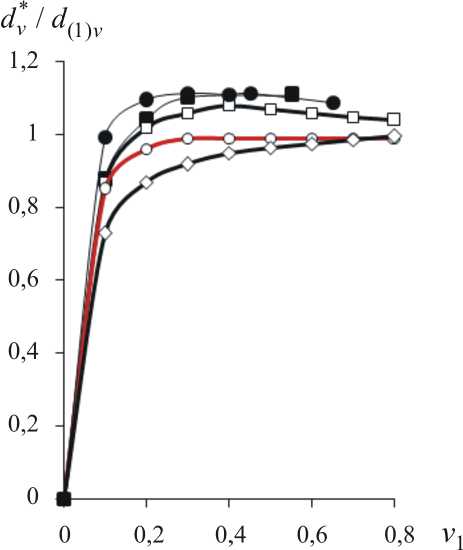
Список литературы Влияние механической нагрузки на результирующие пьезомодули композита
- Washizu К. Variational methods in elasticity and plasticity. – Oxford: Pergamon Press, 1982. – 630 p. = Baсидзу К. Вариационные методы в теории упругости и пластичности. – М.: Мир, 1987. – 542 с.
- Гузь А.Н. Об определении приведенных упругих постоянных композитных слоистых материалов с начальными напряжениями // Доклады АН УСССР. Сер. А. – 1975. – № 3. – С. 216–219.
- Гузь А.Н. Упругие волны в телах с начальными напряжениями: в 2 т. – Киев. Наукова думка, 1986. – Т. 1. Общие вопросы. Киев: Наук. думка. – 376 с. – Т. 2. Закономерности распространения. – Киев: Наук. думка. – 536 с.
- Экспериментальные исследования свойств материалов при сложных термомеханических воздействиях / В.Э. Вильдеман, М.П. Третьяков, Т.В. Третьякова, Р.В. Бульбович, С.В. Словиков, А.В. Бабушкин, А.В. Ильиных, Д.С. Лобанов, А.В. Ипатова; под ред. В.Э. Вильдемана. – М.: Наука. Физматлит, 2012. – 204 с.
- Вильдеман В.Э., Староверов О.А. Влияние дополнительных вибрационных воздействий на процессы деформирования и разрушения композиционных трубчатых образцов / Сборник трудов 32-й Международной инновационной конференции молодых ученых и студентов по проблемам машиноведения (МИКМУС – 2020). – М., 2020. – 2021. – С. 32–36.
- Алехин В.В., Аннин Б.Д., Колпаков А.Г. Синтез слоистых материалов и конструкций. – Новосибирск. Ин-т гидродинамики СО АН СССР, 1988. – 128 c.
- Akbarov S.D., Guliev M.S. Axisymmetric longitudinal wave propagation in a finite prestretched compound circular cylinder made of incompressible materials // International Applied Mechanics. – 2009. – Vol. 45, no. 10. – P. 1141–1151.
- Akbarov S.D. Recent investigations on dynamic problems for an elastic body with initial (residual) stresses // International Applied Mechanics. – 2007. – Vol. 43, no. 12. – P. 1305–1324.
- Akbarov S.D. Stability loss and buckling delamination: Three-dimensional linearized approach for elastic and viscoelastic composites. – Springer, 2013. – 448 p.
- Гулиев М.С., Сейфулаев А.И., Абдуллаева Д.Н. Исследование распространения упругих волн в составном цилиндре с начальным кручением // Строительная механика инженерных конструкций и сооружений. – 2018. – № 5. – С. 404–413.
- Белянкова Т.И., Калинчук В.В. Свойства преднапряженных изотропных материалов при учете упругих модулей высших порядков // Наука Юга России. – 2017. – № 2. – С. 3–12.
- Гузь А.Н. Об ультразвуковом неразрушающем методе определения напряжений в элементах конструкций и в приповерхностных слоях материалов: фокус на украинские исследования (обзор) // Прикладная механика. – 2014. – Т. 50, № 3. – С. 3–30.
- Kuliev G.G., Jabbarov M.D. To elastic waves propagation in strained nonlinear anisotropic media // Proceedings the sciences of Earth of academy sciences Azerbaijan. – 1998. – № 2. – P. 103–112.
- Guz A.N. Fundamentals of the three-dimensional theory of stability of deformable bodies. – Springer, New York, 1999. – 555 p.
- Akbarov S.D. Dynamics of pre-strained bi-material elastic systems: Linearized three-dimensional approach. – Springer, 2016. – 1004 p.
- Hoger A. On the determination of residual stress in an elastic body // Journal of Elasticity. – 1986. – Vol. 16. – P. 303–324.
- Robertson R.L. Determining residual stress from boundary. Measurements: a linearized approach // Journal of Elasticity. – 1998. – Vol. 52. – P. 63–73.
- Bažant Z.P. A correlation study of formulations of incremental deformation and stability of continuous bodies // Journal of Applied Mechanics. – 1971. – Vol. 38. – P. 919–928.
- Huang C., Wang L., Wang K. Residual stress identification in thin plates based on modal data and sensitivity analysis // International Journal of Solids and Structures. – 2022. – Vol. 236–237. – Р. 111350.
- Tovstik P.E. Vibration and stability of the prestressed plate lying on the elastic base // Applied Mathematics and Mechanics. – 2009. – Vol. 6. – P. 106–120.
- Nedin R., Dudarev V., Vatulyan A. Some aspects of modeling and identification of inhomogeneous residual stress // Engineering Structures. – 2017. – Vol. 151. – P. 391–405.
- Propagation of torsional surface waves in a homogeneous layer of finite thickness over an initially stressed heterogeneous halfspace / S. Gupta, D.K. Majhi, S. Kundu, S.K. Vishwakarma // Applied Mathematics and Computation. – 2012. – Vol. 218, no. 9. – P. 5655–5664.
- Hu W.T., Chen W.Y. Influence of lateral initial pressure on axisymmetric wave propagation in hollow cylinder based on first power hypo-elastic model // Journal of Central South University. – 2014. – Vol. 21, no. 2. – P. 753–760.
- Yesil U.B. Forced and natural vibrations of an orthotropic pre-stressed rectangular plate with neighboring two cylindrical cavities // Comput. Mater. Continua. – 2017. – Vol. 53, no. 1. – P. 1–22.
- Kolpakov A.G. Effect of influation of initial stresses on the homogenized characteristics of composite // Mechanics of materials. – 2005. – Vol. 37, no. 8. – P. 840–854.
- Kolpakov A.G. On the dependence of the velocity of elastic waves in composite media on initial stresses // Computers & Structures. – 1992. – Vol. 44, no. 1–2. – P. 97–101.
- Kolpakov A.G. Averaged characteristics of stressed laminated media // Journal of Engineering Physics. – 1995. – Vol. 68, no. 5. – P. 605–613.
- Колпаков А.Г. Усредненные модели упругих композиционных материалов и элементов конструкций: дис. … д-ра физ.-мат. наук: 01.02.04. – Новосибирск, 2002. – 291 с.
- Kuang Z.-B. Theory of Electroelasticity, Springer: Heidelberg. – New York, 2014. – 438 p.
- Nedin R.D., Dudarev V.V., Vatulyan A.O. Vibrations of inhomogeneous piezoelectric bodies in conditions of residual stress-strain state // Applied Mathematical Modelling. – 2018. – Vol. 63. – P. 219–242.
- Dasdemir A. Forced vibrations of pre-stressed sandwich plate-strip with elastic layers and piezoelectric core // International Applied Mechanics. – 2018. – Vol. 54, no. 4. – P. 480–493.
- Patent US N 5632841. Thin layer composite unimorph ferroelectric driver and sensor / Richard F. Hellbaum, Robert G. Bryant, Robert L. Fox. – Date of Patent: May 27, 1997.
- Патент RU № 2723567. Лопасть воздушного винта с управляемой геометрией профиля / Паньков А.А., Аношкин А.Н., Писарев П.В., опубл.: 16.06.2020 Бюл. № 17, заявка № 2019137042 от 18.11.2019 г.
- Патент RU № 2778161. Способ увеличения пьезочувствительности биморфа изгибного типа / Паньков А.А., опубл.: 15.08.2022 Бюл. № 23, заявка № 2022101875 от 27.01.2022 г.
- Guo X., Wei P. Dispersion relations of elastic waves in one-dimensional piezoelectric/piezomagnetic phononic crystal with initial stresses // Ultrasonics. – 2016. – Vol. 66. – P. 72–85.
- Берлинкур Д., Керран Д., Жаффе Г. Пьезоэлектрические и пьезомагнитные материалы и их применение в преобразователях // Физическая акустика. Т.1: Методы и приборы ультразвуковых исследований. Часть А. – М.: Мир, 1966. – С. 204–326.
- Хорошун Л.П., Маслов Б.П., Лещенко П.В. Прогнозирование эффективных свойств пьезоактивных композитных материалов. – Киев: Наук. думка, 1989. – 208 с.
- Паньков А.А. Статистическая механика пьезокомпозитов. – Пермь: Изд-во Перм. гос. техн. ун-та, 2009. – 480 с.
- Using an electromechanical analogy to describe the damping characteristics of an MFC actuator / A.A. Pan’kov, A.N. Anoshkin, P.V. Pisarev, S.R. Bayandin // IOP Conference Series: Materials Science and Engineering, 1093 (2021) 012023. – P. 1–6.
- Волков С.Д., Ставров В.П. Статистическая механика композитных материалов. – Минск: Изд-во Белорус. гос. ун-та, 1978. – 208 с.
- Шеpмеpгоp Т.Д. Теоpия упpугости микpонеодноpодных сpед. – М.: Наука, 1976. – 399 с.
- Победря Б.Е., Горбачёв В.И. О статических задачах упругих композитов // Вестник МГУ. Сер. 1: Матем. И механ. – 1977. – № 5. – С. 101–110.
- Паньков А.А. Коэффициенты электромагнитной связи композита с пьезоактивными фазами // Физическая мезомеханика. – 2011. – Т. 14, № 2. – С. 93–99.
- Белоконь А.В., Бондарев П.М. Эффективные физико–механические характеристики 1–3 пьезокомпозита для низко-частотных прикладных проблем // Механика композиционных матеpиалов и констpукций. – 2002. – Т. 8, № 3. – С. 291–308.
- Гетман И.П., Мольков В.А. Об эффективных характеристиках пьезоактивных композитов с цилиндрическими включениями // Прикладная математика и механика. – 1992. – Т. 35, № 3. – С. 501–509.
- Сараев Л.А. К теории упругости микронеоднородных сред, учитывающей стохастические изменения связности составляющих компонентов // Вестник Пермского национального исследовательского политехнического университета. Механика. – 2021. – № 2. – С. 132–143.


