Влияние мультифрактальных характеристик матричных волокон на прочность стеклобазальтокомпозитных труб

Развитие научно-технического прогресса связано в большей степени с цифровыми технологиями и методами обработки результатов экспериментов [1]. Внедрение нановолокон углерода в стеклобазальтопластиковые композитные трубы [2] позволило использовать их для производства труб с улучшенными эксплуатационными характеристиками, а также для эксплуатации при низких температурах [3], [4].

Многокомпонентный состав стеклобазальтопластиковых композитных труб приводит к их структурной неоднородности [5]. При количественном анализе неоднородных участков структуры исследователи сталкиваются с трудностями, обусловленными сложностью их строения [6]. В связи с этим задача моделирования физико-механических свойств этих труб на основе анализа их структуры является важной и актуальной проблемой в материаловедении [7]. Однако существующие эмпирические модели, описывающие зависимость структуры от свойств, не всегда Vafaeva, Kh. M.; Nuguzhinov, Zh. S.

Effect of matrix fiber multifractal characteristics on the strength of glass-basalt composite pipes;

позволяют достигать высокой точности прогнозирования [8], что связано с ограничениями этих моделей [9]. Одной из причин невысокой точности предсказаний является сложная геометрическая конфигурация элементов структуры строительных материалов [10], что обусловлено особенностями их структурообразования [11] и ограничениями существующих методов идентификации структуры [12].

Как показывают многочисленные исследования, использование фрактального формализма эффективно позволяет описывать сложные структуры материалов на различных масштабных уровнях [13]–[16]. Сюда можно отнести ранжирование критериев качества [14], регуляризацию материаловедческих задач [15], оценку свойств конструкционных материалов [16], [17].

Например, на основе фрактального анализа макроструктуры бетона марки 400 [18] и керамзитобетона [19] были получены адекватные модели прогнозирования их прочностных характеристик. Фрактальная геометрия также позволяет проводить ранжирование свойств материалов в зависимости от размеров рабочей области их параметров [20], [21] и регуляризировать некорректные задачи в материаловедении [22]. Кроме того, она помогает устанавливать взаимосвязь между структурой и свойствами материалов, предназначенных для различных целей [23].

В частности, фрактальная геометрия успешно описывает неоднородные структуры [24], а также исследует влияние щелочных сульфатов на усадку, гидратацию, пористую структуру и микроструктуру [25–27]. Несмотря на значительные успехи в изучении композитных материалов, отсутствует комплексный метод, позволяющий с высокой точностью прогнозировать прочностные характеристики стеклобазальтопластиковых труб на основе анализа их микроструктуры. В частности, недостаточно изучено влияние мультифрактальных характеристик микроструктуры на прочность при растяжении этих материалов. Учитывая сложность структуры стеклобазальтопластиковых композитных труб и ограничения существующих методов анализа, необходимо разработать новый метод, позволяющий более точно прогнозировать их прочностные характеристики. Мультифрактальный анализ, успешно применяемый для описания сложных структур в различных областях материаловедения [28]–[30] представляется перспективным инструментом для решения этой задачи.

Целью данного исследования является разработка метода прогнозирования прочности при растяжении стеклобазальтопластиковых композитных труб на основе мультифрактального анализа их микроструктуры.

Для достижения этой цели необходимо решить следующие задачи:

• -    Провести экспериментальное исследование микроструктуры стеклобазальтопластиковых композитных труб.

• -    Выполнить мультифрактальный анализ микроструктуры труб и определить их мультифрактальные характеристики.

• -    Экспериментально определить прочность при растяжении труб.

• -    Установить взаимосвязь между мультифрактальными характеристиками микроструктуры и прочностью при растяжении труб.

• -    Разработать математическую модель для прогнозирования прочности при растяжении труб на основе мультифрактального анализа.

• -    Оценить точность и надежность разработанной модели.

Исследование направлено на решение актуальной проблемы в области материаловедения -разработку более точных моделей прогнозирования механических свойств композитных труб путем использования мультифрактального анализа микроструктуры материала.

• 2    Materials and Methods

Исследовалась микроструктура стеклобазальтопластиковых композитных труб (Рис. 1). Проведены гидравлические испытания таких труб (Рис. 2). В центральной части изделий сточен исходный наружный диаметр со 164 мм до 161 мм (из стенки 7 мм сточили 1.5 мм силового слоя, осталось всего 5.5 мм), ширина проточки около 30 мм. Это внешний силовой слой с кольцевой намоткой, которая отвечает за прочность в окружном направлении, в т.ч. от сминающего давления. Стенки толщиной 5.5 мм, ослабленной в кольцевом направлении, оказалось недостаточно.

В итоге по результатам испытаний 3 из 8 образцов сломались при давлении снаружи около 41 бар, а им требуется 150 бар.

Решение для достижения этого показателя — увеличение диаметра и усиление кольцевой намотки с разной толщиной стенки (от 12 до 15 мм).

В изготовлении труб были использованы:

• -    стеклоровинг (волокно) 1200 текс (стекло марки Е),

• -    эпоксидная смола KER 828 из Южной Кореи;

• -    отвердитель ИЗОМТГФА,

• -    ускоритель Алкофен.

Примерное соотношение материалов по весу: 70% ровинг, 30% связующее, доля Алкофена мизерная.

В связующем соотношение смолы к ИЗОМТГФА по весу — 100/80.

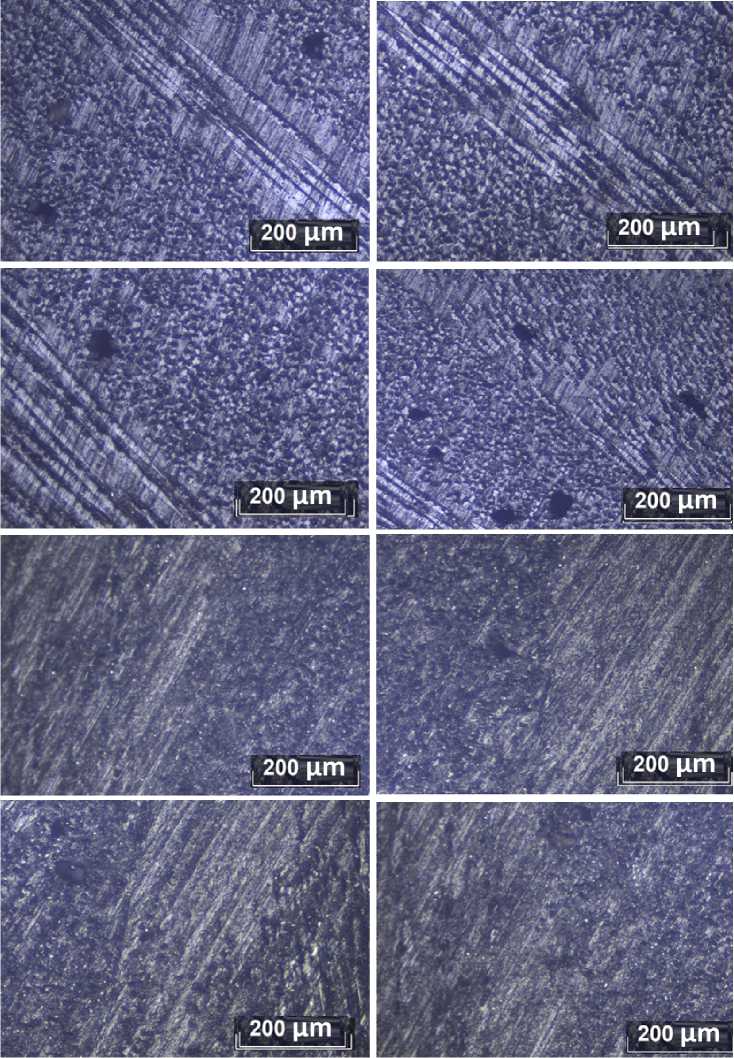
Рис. 1- Микроструктура образцов стеклобазальтопластиковых композитных труб (Образцы 18)

Fig. 1 - Microstructure of glass-basalt-plastic composite pipe samples (Samples 1-8)

Рис. 2 - Фотографии разрушений гибридных стеклобазальтопластиковых труб

Fig. 2 - Photos of destruction of hybrid glass-basalt-plastic pipes

Микростроение труб исследовалась с применением мультифрактального анализа. Рассчитан спектр фрактальных размерностей Реньи [19] волокон матрицы труб для 8 образцов и описан в [18]:

N

₁      ln ∑ p i^q

D (q)  --lim ——--, q - 1 δ→∞ ln δ

N где In ^ pi - обобщенная статистическая сумма вероятностей р{ попадания исследуемого i=1

элемента структуры в i -ю ячейку квадратной сетки покрытия с размером ячейки δ . D 0 – фрактальная размерность волокон матрицы; D 1 – информационная размерность волокон матрицы при q = 1 ; которая описывает информационную энтропию, характеризующую скорость роста количества информации и описывающую возрастающую информацию для определения местоположения точки объекта при δ ; D 2 – корреляционную размерность, при q=2 , описывающая вероятность нахождения в квадратной ячейке сразу двух точек; D -^ и D_+m - размерности наиболее темных и светлых участков неоднородной структуры соответственно.

На Рис. 3 приведен пример расчета спектра фрактальных размерностей Реньи для Образца 7, представленного на Рис. 1. Показатель степени q задавался в диапазоне численных значений от - 200 до 200, поскольку в при анализе в более широких пределах (от - 1000 до 1000) значения фрактальных размерностей изменялись несущественно (4…6 %). Граничные размеры клеток задавались в пределах от 20 по 60 пикселей с шагом 5 пикселей (Рис. 4). При этом спектр 1 рассчитывался для значений клетки 60 пикселей; спектр 2 – клетка 55 пикселей; спектр 3 – клетка 50 пикселей; спектр 4 – клетка 45 пикселей; спектр 5 – клетка 40 пикселей; спектр 6 – клетка 35 пикселей; спектр 7 – клетка 50 пикселей; спектр 8 – клетка 25 пикселей. Для дальнейших расчетов фрактальных размерностей в эксперименте выбирался спектр 6 с размером клетки 50 пикселей, что соответствует линейным размерам элементов структуры (волокнам матрицы и элементам эпоксидной составляющей).

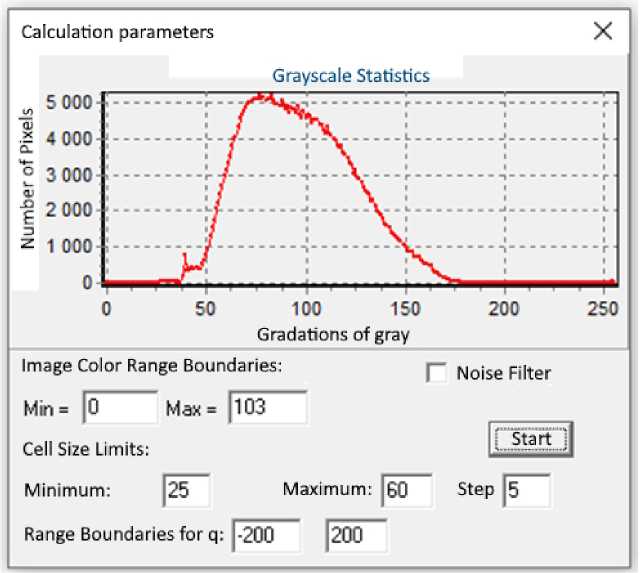
Рис. 3 - График распределения цвета в 256 градациях серого для фотоснимка Образца 7

Fig. 3 - Color distribution graph in 256 shades of gray for photograph Sample 7

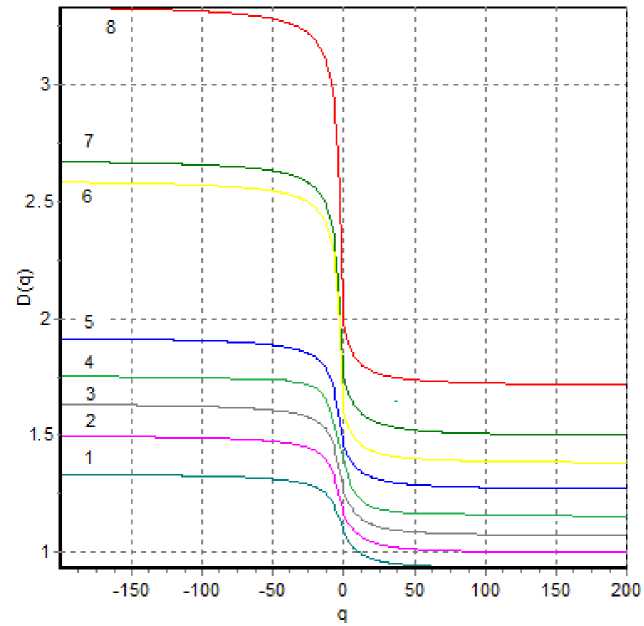
Рис. 4 - Спектр фрактальных размерностей Реньи для светлых волокон матрицы Образца 7

Fig. 4 - Spectrum of Renyi fractal dimensions for light fibers of the matrix of Sample 7

Распределение цвета в 256 градациях серого проводилось для каждого из 8 фотоснимков микростроения труб. После этой процедуры задавался диапазон цвета в градациях серого для исследуемой структурной составляющей (Рис. 4).

3 Results and Discussion

Задачи фрактального моделирования используют, в основном, для формирования моделей микрообъектов (например, внутреннего микростроения материалов на различных масштабных уровнях вплоть до атомных). Однако при этом могут встречаться задачи фрактального формализма, обращенные на идентификацию макрообъектов (технологических процессов, явлений Природы, строения Вселенной и т.п.).

При оценке структуры микрообъектов, согласно предложенным элементам организации фрактального моделирования, использовался следующий алгоритм:

• –    для повышения точности идентификации, например, микроструктуры материала, с целью частичной компенсации неполноты формальной аксиоматики, обусловленной недостатком информации от традиционных вербальных, полуколичественных и количественных методик оценки элементов этой структуры, предлагается применять теорию фракталов;

• –    для оценки критериев качества, исключающей натурные испытания, в моделях описывающих связь между структурой и изучаемыми свойствами, можно применять фрактальное моделирование, анализ которого включает:

• а )    определение границ самоподобия структуры или отдельных фаз;

• б)    вычисление и анализ фрактальной размерности элементов структуры;

• в )    определение спектра статистических размерностей мультифрактала;

• г )    установление чувствительности свойств материала к спектру размерностей;

• д )    построение математической модели фрактального типа по полученным экспериментальным данным;

• е )    оценка точности прогноза исследуемых свойств на основании влияния спектра размерностей.

При фрактальном анализе всегда предполагается, что изучаемому фрактальному объекту, независимо от масштаба его представления, присуще свойство самоподобия, которое заключается в том, что в любом масштабе его структуре присущи одни и те же геометрические особенности. Конечно, для реального природного фрактала, которым, безусловно, является структура многих металлов, существует некоторый масштаб длины l , такой, что при увеличениях несколько меньших или больших от этого масштаба свойство самоподобия пропадает. Поэтому свойство самоподобия природных фракталов рассматриваются на масштабах (2).

^l min — ^l — ^l max ^.                                                    (2)

На каждом масштабном уровне в результате исследования выявлены новые особенности структуры материала, характеризующие то, или иное его качество.

Таким образом, для выбора масштаба представления, например зеренной структуры стали, для определения ее фрактальной размерности, необходимо определить интервал (2), в котором соблюдается ее самоподобие и на этом интервале выбрать тот единственный масштаб, на котором вычисление фрактальной размерности даст наиболее точный результат.

Для оценки масштаба представления эмпирически задается некоторый шаг Δ l изменения масштаба от l _min до l _max Затем в интервале (3) вычисляются оценки фрактальных размерностей в точках масштабов:

lmin + (lmin + Al) + (lmin + 2 ‘Al)+,..., +(lmin + n ‘Al) , где n =

max min

A l

За рекомендуемый масштаб преставления структуры принимается тот, при котором, как минимум в двух рядом стоящих точках из ряда (3), фрактальные размерности минимально различаются между собой. Последнее объясняется тем, что при этом наилучшим образом соблюдается свойство самоподобия структуры. Ниже приведен пример выбора масштаба увеличения гибридных стеклобазальтопластиковых труб в интервале от 30 до 300 мкм (Рис. 5).

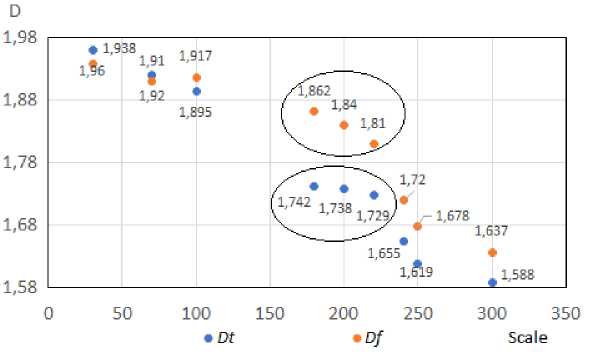
Рис. 5 - Масштаб представления структуры гибридных стеклобазальтопластиковых труб

Fig. 5 - Scale representation of the structure of hybrid glass-basalt-plastic pipes

Даже визуально видно, что самоподобие в указанном интервале масштабов сохраняется. За рекомендуемый масштаб представления структуры был выбран масштаб 200 мкм, поскольку в двух рядом стоящих масштабах (180 мкм, 220 мкм), фрактальные размерности минимально различались между собой: для фрактальной размерности Df составили 1.862, 1.810 соответственно (Рис. 5). Для фрактальной размерности эпоксидной составляющей Dt для масштаба представления 180 мкм значение равно 1.742, для масштаба 220 мкм - 1.729.

Самоподобие структуры труб можно проверить не только визуально, но и аналитически. Для этого достаточно выбрать одну или несколько характерных геометрических фигур на фотоснимке структуры и проверить их геометрическое подобие. Например, на Рис. 6 выбран участок структуры А.

Рис. 6 - Оценка областей самоподобия структуры гибридных стеклобазальтопластиковых труб

Fig. 6 - Evaluation of self-similarity regions of the structure of hybrid glass-basalt-plastic pipes

Соотношение размеров границ этого участка и элементов структуры, заключенных в нем, на всех масштабах увеличения сохраняется, что подтверждает факт самоподобия структуры, а значит и ее фрактальность.

В процессе мультифрактального анализа макроструктуры раствора проведена оценка спектра статистических размерностей Реньи. При обработке полученных данных сформирована Таблица 1, отражающая основные результаты эксперимента.

Таблица 1. Спектр размерностей структуры и характеристики прочности на изгиб Table 1. Spectrum of Structural Dimensions and Bending Strength Characteristics

Sample №	D -200	D 0	D 1	D 2	D 200	G p , MPa
1	3.200	1.922	1.900	1.879	1.705	4.60
2	2.885	1.905	1.880	1.860	1.690	4.50
3	2.830	1.880	1.855	1.840	1.660	4.35
4	2.525	1.854	1.830	1.810	1.620	4.20
5	2.334	1.823	1.799	1.770	1.600	3.95
6	2.400	1.830	1.805	1.780	1.610	3.70

Sample №	D -200	D 0	D 1	D 2	D 200	а р , MPa
7	2.670	1.740	1.720	1.680	1.500	3.50
8	2.580	1.605	1.581	1.558	1.385	3.45

Для влияния спектра фрактальных размерностей Реньи на показатели прочности при растяжении определялся коэффициент чувствительности K_i по формуле (4) [19]:

JV Y i

I Xi - Xi +11

где Xi и Xi+1 - значения фрактальных размерностей светлых волокон матрицы в рассматриваемых соседних областях i и i +1; Yi и Yi+1 - значения прочности на растяжение ар в этих областях. На рис. 7 приведены результаты ранжирования фрактальных размерностей по степени их влияния на прочность при растяжении.

Рис. 7 - Ранжирование фрактальных размерностей по степени их влияния на прочность при растяжении

Fig. 7 - Ranking of fractal dimensions by their influence on tensile strength

Высокие показатели чувствительности прочности зафиксированы к фрактальным размерностям D -200 для всех 8 исследуемых образцов. Для остальных образцов показатели чувствительности прочности к размерностям составили: 0.033…0.367 для D 0 ; 0.100…2.033 для D 1 ; 0.044…0.768 для D 2 ; 0.016…0.264 для D 200 .

На Рис. 8 приведены соотношения между показателями прочности на растяжение стеклобазальтопластиковых композитных труб и фрактальными размерностями волокон матрицы, вычисленными из спектра Реньи D(q) . Аппроксимация всех результатов эксперимента линейными зависимостями свидетельствует о существовании связи между фрактальной структурой и их прочностью. Во всех рассматриваемых случаях зависимости аппроксимируются линейными моделями.

a p, MPa

4.75 y = 1.0541x + 1.2084

4.5

• _4.25              R   0.45

3.75 3.5 3.25 2.25    2.45    2.65    2.85    3.05    3.25

D-200

а

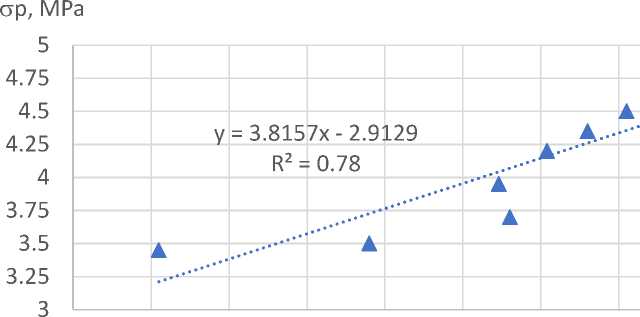
1.55    1.6    1.65    1.7    1.75    1.8    1.85    1.9    1.95

Do

б

σ p, MPa

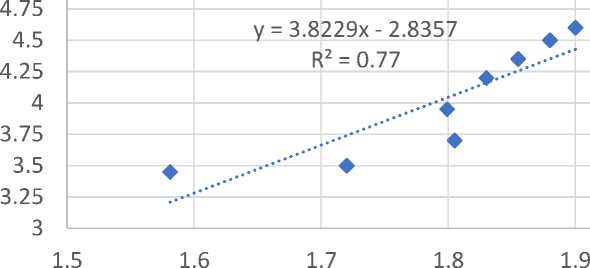
D1

в

σ p, MPa

4.75

4.5

4.25

3.75

3.5

3.25

1.5

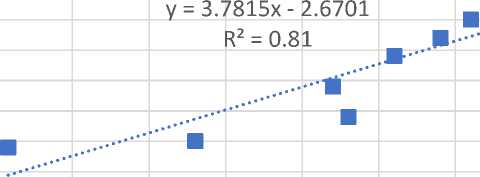
1.55    1.6    1.65    1.7    1.75    1.8    1.85    1.9

D2

г

σ p, MPa

4.75

4.5

4.25

3.75

3.5

3.25

1.300

y = 3.7711x - 1.9883_______ ж __________

R² = 0.80

1.400     1.500     1.600     1.700     1.800

D200

д

Рис. 8 - Соотношения между показателями прочности на растяжение и фрактальными размерностями волокон матрицы: а - D -200 , б - D 0 в - D 1 , г - D 2 и д – D 200

Fig. 8 - Relationships between tensile strength indices and fractal dimensions of matrix fibers а - D- 200 , б - D 0 в - D 1 , г - D 2 и д – D 200

Использование метода с применением теории фракталов позволило установить новые связи между структурой стеклобазальтопластиковых композитных труб и его прочностью.

• 4    Conclusions

• 1.    Разработан метод прогнозирования показателей прочности на растяжение стеклобазальтопластиковых композитных труб на основе анализа их микроструктуры.

• 2.    Проведенное вычисление коэффициентов чувствительности между фрактальными размерностями волокон матрицы труб (D -200 , D 0 , D 1 , D 2 , D 200 ) из мультифрактального спектра Реньи и числовыми значениями прочности на растяжение позволило оценить степень их влияния на прочностные характеристики труб.

• 3.    Было выявлено, что прочность на растяжение сильно зависит от фрактальной размерности D -200 для всех 8 исследуемых образцов.

• 4.    Полученные уравнения регрессии могут быть использованы в качестве экспресс-метода для оценки прочности на растяжение стеклобазальтопластиковых композитных труб и позволят прогнозировать показатели прочности и актуализируя результаты в зависимости от данных последующих экспериментов.

• 5.    Данный метод может служить альтернативным методом для оценки прочности труб в случаях, когда проведение механических испытаний невозможно.

• 5    Fundings

  This research was supported by a grant from the Russian Science Foundation No. 24-19-00691, https://rscf.ru/project/24-19-00691/.