Влияние неопределенности исходных данных на эффективность статистического имитационного моделирования нерефлекторной системы. Часть 2. Дифференциация стохастических факторов по влиянию на эффективность применения СИМ-модели

Автор: Ваулина Кристина Владимировна, Маслов Олег Николаевич

Журнал: Инфокоммуникационные технологии @ikt-psuti

Рубрика: Новые информационные технологии

Статья в выпуске: 1 т.15, 2017 года.

Бесплатный доступ

Во второй части статьи представлены методика и результаты исследования статистической имитационной модели (СИМ) бизнес-процесса «Предоставление государственных и муниципальных услуг» Многофункционального Центра областного уровня, реализованной в среде AnyLogic.

Нерефлекторные системы, статистическое имитационное моделирование, метод димова-маслова, неопределенность исходных данных, эффективность модели

Короткий адрес: https://sciup.org/140191865

IDR: 140191865 | DOI: 10.18469/ikt.2017.15.1.08

Текст научной статьи Влияние неопределенности исходных данных на эффективность статистического имитационного моделирования нерефлекторной системы. Часть 2. Дифференциация стохастических факторов по влиянию на эффективность применения СИМ-модели

В первой части настоящей статьи [1] представлена СИМ-модель бизнес-процесса «Предоставление государственных и муниципальных услуг» Многофункционального Центра (МФЦ) областного уровня, выбранная в качестве тестового объекта для исследования влияния неопределенности исходных данных на эффективность СИМ нерефлекторной СС социально-экономического типа. Цель второй части статьи – анализ на примере тестовой СИМ-модели влияния неопределенности и кумулятивности (под которой понимается свойство минимального объема информации быть максимально полезной для достижения поставленной цели) исходных данных на эффективность СИМ.

Методика проведения эксперимента

Идею экспериментального исследования эффективности разработанной СИМ-модели иллюстрирует рис. 1: имеется М вариантов решения поставленной задачи с применением СИМ-модели, из которых лицом, принимающим решения (ЛПР), для дальнейшего рассмотрения выбирается наилучшее решение m с результатом Y _mk , где m [1; M ] и k [1; K ] – соответственно, номер варианта решения и номер результата решения поставленной задачи. Отметим, что на практике ЛПР рассматривает не одно, а минимум два решения: основное и запасное, но в данном случае это несущественно. В состав исходных данных для каждого варианта входят случайные величины (СВ) X _n ; n [1; N ], которые моделируют стохастические факторы и в рамках СИМ «разыгрываются» (далее без кавычек) по методу Монте-Карло.

В [1] было высказано предположение, что на результаты СИМ достаточно сложным и заранее непредсказуемым образом, но должны влиять способы учета неопределенности знаний ЛПР об указанных факторах, то есть вероятностные законы разыгрывания СВ. Утверждалось, что ранжирование этих способов ведет разработчиков систем управления бизнес-процессами от модели в виде равномерного закона (РЗ) согласно принципу безразличия (что соответствует максимальной неопределенности знаний ЛПР) к финитным устойчивым моделям (включая нормальный закон) в условиях применимости предельных теорем теории вероятностей, и далее – к статистическим моделям, полученным в результате идентификация законов распределения СВ (см. традиционную методику СИМ [2]), и предложению использовать реальные данные, полученные при обследовании объекта СИМ, если такая возможность имеется, – что соответствует минимальной и неустранимой в принципе неопределенности знаний ЛПР.

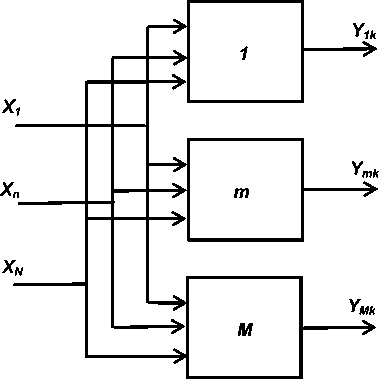
Рис. 1. Схема эксперимента с СИМ-моделью тестового бизнес-процесса

Предполагалось также, что по влиянию на результаты СИМ случайные факторы могут быть разделены на основные и второстепенные, что целесообразно учитывать как при разыгрывании соответствующих им СВ, так и при организации и проведении тестовых и рабочих экспериментов с СИМ-моделью.

Применительно к схеме на рис. 1 изложенное означает выбор решения m с наилучшим результатом Y _mk по традиционной методике СИМ в качестве эталона, а затем – отступление от этой методики в сторону упрощения и ускорения процедуры СИМ с контролем за получаемым результатом: если решение с номером m по-прежнему является наилучшим, сделанное отступление от эталона считается допустимым, если оно изменяется – признается недопустимым.

Поскольку число СВ достаточно велико (в [1] для тестовой СИМ-модели N = 23), конечное решение поставленной задачи при требуемом многократном прогоне СИМ-модели и реальных значениях М представляется излишне трудоемким и долгим. Поэтому в качестве первого приближения был рассмотрен случай М = 1; K = 7 с оценкой влияния на Y _1k замены законов разыгрывания СВ, полученных по результатам предварительного статистического исследования и моделирования X _1-23 [1], на равномерный закон для тех же конечных пределов.

Методика СИМ-эксперимента предусматривала три этапа его проведения.

Этап I. Формирование массивов эталонных значений Y _1k путем прогона СИМ-модели с изначально зафиксированными исходными данными, полученными согласно традиционной методике СИМ (фигурируют с обозначением «эталон»).

Этап II. Выбор допустимого значения отклонения от эталона. В соответствии с [1] контролируемыми данными СИМ-модели считались K = 7 следующих переменных:

– число заявок на оказание услуги;

– число оказанных услуг;

– число отказов на запросы о предоставлении услуг;

– число запросов, отправленных с курьером;

– количество выполненных электронных запросов;

– число невыполненных электронных запросов;

– число запросов в органы государственной власти (ОГВ).

Этап III. Подсчет числа минимальных и максимальных (Мin и Мax) отклонений. Цель данного этапа – определение границ, на основании которых можно сделать выводы о влиянии изменения закона распределения СВ X _1-23 на выходные данные СИМ-модели Y _1k.; K = 7. Границы рассчитывались путем вычитания и суммирования эталона и величины отклонения, они фигурируют с обозначениями «Отклонение Мin» и «Отклонение Мax» соответственно . Обозначение «Все по РЗ» соответствует ситуации, когда в одном прогоне все СВ изменялись по РЗ; «СВn – РЗ» – когда в одном прогоне одна СВ изменялась по РЗ.

Результаты экспериментов с тестовой СИМ-моделью

Этап IV. Проведение эксперимента с учетом различных условий.

В ходе экспериментов будет меняться закон распределения следующих случайных величин: СВ1 – длительность приема документов; СВ2 – время ожидания недостающих документов; СВ3 – длительность приема недостающих документов; СВ4 – длительность анализа КД регистратором; СВ5 – длительность анализа поступившего дела; СВ6 – длительность подготовки документов для отправки МВ-запроса в ОГВ; СВ7 – длительность подготовки электронного запроса; СВ8 – длительность подготовки посылки в ОГВ; СВ9 – длительность доставки посылки в ОГВ; СВ10 – длительность анализа КД в ОГВ; СВ11 – время ожидания недостающих документов из МФЦ; СВ12 – длительность оформления результата запроса; СВ13 – длительность перевозки результата запроса; СВ14 – время ожидания заявителя; СВ15 – время выдачи результата услуги заявителю. В экспериментах фигурирует также СВ23 – интенсивность поступления заявок (чел/час), которая изменяется согласно расписанию интенсивности.

Допустимыми считались отклонения от эталона в пределах ±20%.

Необходимо проследить влияние изменений исходных данных на переменные СИМ-модели (выходные значения): kpost – текущее число поступивших заявок на оказание услуги; kokaz – текущее число ока-

Таблица 1.1. Эксперимент №1. Случайные величины

	2 и	ст m и	m и	^t m и	ID м и	40 М и	м и	00 99 и	04 М и	о m и	г^ ^Н 09 и	Г1 m о	ГП m и	ТГ iH 09 и	ID и	г**, П CQ U
Эталон	2828	5	5	5	2664	267	195	94	18	90	5	72	68	2577	2574	2829
^x-^z тш	2262	4	4	4	2131	212	156	75	14	72	4	58	54	2062	2059	2263
Э max	3394	6	6	6	3197	320	234	113	22	108	6	86	82	3092	3089	3395
Все по РЗ	2674	0	0	0	2511	218	156	97	19	55	6	30	30	2274	2270	2698

Таблица 1.2. Эксперимент №1. Выходные данные СИМ-модели

	kpost	kokaz	kotk	kzapogv	knelzap	kvelzap	kzapkur
Эталон	2829	2574	25	271	19	177	94
э . min	2263	2059	20	216	15	142	75
э max	3395	3089	30	325	23	212	113
Все по РЗ	2698	2270	28	224	29	127	97

Таблица 2.1. Эксперимент №2. Случайные величины

	iH х и	г 1 о	и	m о	ш в и	ЧО X и	х и	00 X и	04 X и	О гН х о	S и	ГМ и	х о	гН х и	ш F4 со и	СП eq И и
Эталон	2828	5	5	5	2664	267	195	94	18	90	5	72	68	2577	2574	2829
тт	2262	4	4	4	2131	214	156	75	14,4	72	4	58	54	2062	2059	2263
Э max	3394	6	6	6	3197	320	234	113	21,6	108	6	86	82	3092	3089	3395
СВ1 по РЗ	2406	2	2	2	2264	242	164	108	21	105	9	84	81	2183	2181	2447

Таблица 2.2. Эксперимент №2. Выходные данные СИМ-модели

	kpost	kokaz	kotk	kzapogv	knelzap	kvelzap	kzapkur
Эталон	2829	2574	25	271	19	177	94
min	2263,2	2059,2	20	216	15,2	141,6	75,2
max	3394,8	3088,8	30	325,2	22,8	212,4	112,8
СВ1поРЗ	2447	2181	21	250	21	143	108

Таблица 3.1. Эксперимент №3. Случайные величины

	X и	m и	m и	S и	1Л X U	40 X и	X U	00 X U	04 X и	о X и	X и	X и	m X и	-* X u	1Г. X u	rn eq M U
Эталон	2828	5	5	5	2664	267	195	94	18	90	5	72	68	2577	2574	2829
—'min	2262	4	4	4	2131	214	156	75	14	72	4	58	54	2062	2059	2263
max	3394	6	6	6	3197	320	234	113	22	108	6	8	82	3092	3089	3395
CB2 по P3	2822	0	0	0	2659	262	194	91	17	85	5	72	68	2581	2579	2822

Таблица 3.2. Эксперимент №3. Выходные данные СИМ-модели

	kpost	kokaz	kotk	kzapogv	knelzap	kvelzap	kzapkur
Эталон	2829	2574	25	271	19	177	94
min	2263,2	2059,2	20	216	15,2	141,6	75,2
э -'max	3394,8	3088,8	30	325,2	22,8	212,4	112,8
CB2 по P3	2822	2579	25	266	19	175	91

Таблица 4.1. Эксперимент №4. Случайные величины

	2 и	<м m и	m и	't m о	ID pa и	so pa и	2 и	ос ра и	04 аа и	о 2 и	^ iH аа и	гч iH аа и	СП гН аа о	ТГ гН аа о	ш гН аа о	m гч СО и
Эталон	2828	5	5	5	2664	267	195	94	18	90	5	72	68	2577	2574	2829
^тт	2262	4	4	4	2131	214	156	75	14	72	4	58	54	2062	2059	2263
э max	3394	6	6	6	3197	320	234	113	22	108	6	86	82	3092	3089	3395
свз по РЗ	2703	8	8	8	2549	248	180	87	17	85	4	70	70	2493	2487	2710

Таблица 4.2. Эксперимент №4. Выходные данные СИМ-модели

	kpost	kokaz	kotk	kzapogv	knelzap	kvelzap	kzapkur
Эталон	2829	2574	25	271	19	177	94
тт	2263,2	2059,2	20	216	15,2	141,6	75,2
max	3394,8	3088,8	30	325,2	22,8	212,4	112,8
СВЗ по РЗ	2710	2487	23	250	15	165	87

Таблица 5.1. Эксперимент №5. Случайные величины

	2 и	cm aa и	CD aa о	T P0 U	ID pa и	40 aa о	и	oc aa и	04 PC и	e и	2 и	CM и	CD 2 и	2 и	ID 2 и	СП ГЧ CO U
Эталон	2828	5	5	5	2664	267	195	94	18	90	5	72	68	2577	2574	2829
mm	2262	4	4	4	2131	214	156	75	14	72	4	58	54	2062	2059	2263
э max	3394	6	6	6	3197	320	234	113	22	108	6	86	82	3092	3089	3395
CB4 по P3	2828	5	5	5	2664	267	196	94	18	90	5	72	68	2577	2574	2829

Таблица 5.2. Выходные данные СИМ-модели

	kpost	kokaz	kotk	kzapogv	knelzap	kvelzap	kzapkur
Эталон	2829	2574	25	271	19	177	94
mm	2263,2	2059,2	20	216	15,2	141,6	75,2
э ^v max	3394,8	3088,8	30	325,2	22,8	212,4	112,8
CB4 по P3	2829	2574	25	271	19	177	94

Таблица 6.1. Эксперимент №6. Случайные величины

	2 и	CM PC U	CD aa о	"У PC О	ID pa и	40 pa и	2 и	00 aa и	04 pa и	e 2 и	2 и	см 2 и	CD 2 и	2 и	ID 2 и	СП ГЧ со и
Эталон	2828	5	5	5	2664	267	195	94	18	90	5	72	68	2577	2574	2829
mm	2262	4	4	4	2131	214	156	75	14	72	4	58	54	2062	2059	2263
э -'max	3394	6	6	6	3197	320	234	113	22	10 8	6	86	82	3092	3089	3395
CB5 по P3	2825	3	3	3	2644	264	198	88	17	85	2	72	68	2571	2561	2829

Таблица 6.2. Эксперимент №6. Выходные данные СИМ-модели

	kpost	kokaz	kotk	kzapogv	knelzap	kvelzap	kzapkur
Эталон	2829	2574	25	271	19	177	94
9 .	2263,2	2059,2	20	216	15,2	141,6	75,2
9 max	3394,8	3088,8	30	325,2	22,8	212,4	112,8
СВ5 по РЗ	2829	2561	30	266	20	178	88

Таблица 7.1. Эксперимент №7. Случайные величины

	2 и	<4 BQ О	rr> И О	*T BQ U	in BQ U	40 BQ U	BQ О	oo BQ U	04 BQ О	о m и	S и	rl m и	m m и	-r S и	m 2 и	m Г4 co и
Эталон	2828	5	5	5	2664	267	195	94	18	90	5	72	68	2577	2574	2829
mm	2262	4	4	4	2131	214	156	75	14	72	4	58	54	2062	2059	2263
9 max	3394	6	6	6	3197	320	234	113	22	108	6	86	82	3092	3089	3395
CB6 по P3	2840	5	5	5	2648	233	164	95	19	70	6	48	48	2570	2568	2843

Таблица 7.2. Эксперимент №7. Выходные данные СИМ-модели

	kpost	kokaz	kotk	kzapogv	knelzap	kvelzap	kzapkur
Эталон	2829	2574	25	271	19	177	94
9 . min	2263,2	2059,2	20	216	15,2	141,6	75,2
max	3394,8	3088,8	30	325,2	22,8	212,4	112.8
CB6 по P3	2843	2568	34	239	20	144	95

Таблица 8.1. Эксперимент №8. Случайные величины

	гН во и	ГЦ ВО и	<*> во и	■у во и	Ш ВО и	40 m и	и	00 СО и	04 во и	о Й и	Й и	П Й и	m Й и	Й и	in Й и	m гч CQ и
Эталон	2828	5	5	5	2664	267	195	94	18	90	5	72	68	2577	2574	2829
э . min	2262	4	4	4	2131	214	156	75	14	72	4	58	54	2062	2059	2263
э '-'max	3394	6	6	6	3197	320	234	ИЗ	22	108	6	86	82	3092	3089	3395
СВ7 по РЗ	2785	5	5	5	2615	206	138	88	17	85	4	71	71	2557	2531	2794

Таблица 8.2. Эксперимент №8. Выходные данные СИМ-модели

	kpost	kokaz	kotk	kzapogv	knelzap	kvelzap	kzapkur
Эталон	2829	2574	25	271	19	177	94
3min	2263,2	2059,2	20	216	15,2	141,6	75,2
Эшах	3394,8	3088,8	30	325,2	22,8	212,4	112,8
СВ7 по РЗ	2794	2531	23	210	16	122	88

Таблица 9.1. Эксперимент №9. Случайные величины

	Й о	Г1 m и	m и	m о	m CO и	40 CO и	m и	00 CO U	04 BQ U	О ^ co о	m и	ГЦ Й и	m Й и	Й и	К) ^ со и	СП п СО U
Эталон	2828	5	5	5	2664	267	195	94	18	90	5	72	68	2577	2574	2829
mm	2262	4	4	4	2131	214	156	75	14	72	4	58	54	2062	2059	2263
э -'max	3394	6	6	6	3197	320	234	113	22	108	6	86	82	3092	3089	3395
CB8 по P3	2821	9	9	9	2672	217	149	93	18	90	10	72	72	2549	2549	2822

Таблица 9.2. Эксперимент №9. Выходные данные СИМ-модели

	kpost	kokaz	kotk	kzapogv	knelzap	kvelzap	kzapkur
Эталон	2829	2574	25	271	19	177	94
э . пгт	2263,2	2059,2	20	216	15,2	141,6	75,2
max	3394,8	3088,8	30	325,2	22,8	212,4	112,8
СВ8 по РЗ	2822	2549	26	226	15	134	93

Таблица 10.1. Эксперимент №10. Случайные величины

	Й и		m и	’S-СО и	m BQ U	40 CO и	m и	00 BQ О	04 GO U	О ^ co и	m и	ГЧ w co и	m t-H BO и	ТГ Й и	in Й и	cn ГЧ C2 u
Эталон	2828	5	5	5	2664	267	195	94	18	90	5	72	68	2577	2574	2829
9 . min	2262	4	4	4	2131	214	156	75	14	72	4	58	54	2062	2059	2263
э max	3394	6	6	6	3197	320	234	113	22	108	6	86	82	3092	3089	3395
CB9 по P3	2753	9	9	9	2597	200	138	77	15	75	7	63	63	2486	2486	2754

Таблица 10.2. Эксперимент №10. Выходные данные СИМ-модели

	kpost	kokaz	kotk	kzapogv	knelzap	kvelzap	kzapkur
Эталон	2829	2574	25	271	19	177	94
тт	2263,2	2059,2	20	216	15,2	141,6	75,2
9 max	3394,8	3088,8	30	325,2	22,8	212,4	112,8
СВ9 по РЗ	2754	2486	30	206	9	129	77

Таблица 11.1. Эксперимент №11. Случайные величины

	2 u	cq m и	о	и	IT) n U	40 « U	U	00 И и	©4 и	e и	m о	eq 2 и	CO tH M о	■v 2 и	m 2 и	CO n to и
Эталон	2828	5	5	5	2664	267	195	94	18	90	5	72	68	2577	2574	2829
9 . mm	2262	4	4	4	2131	214	156	75	14	72	4	58	54	2062	2059	2263
9 max	3394	6	6	6	3197	320	234	113	22	108	6	86	82	3092	3089	3395
CB10 по P3	2791	8	8	8	2637	250	177	103	20	100	8	79	78	2573	2563	2804

Таблица 11.2. Эксперимент №11. Выходные данные СИМ-модели

	kpost	kokaz	kotk	kzapogv	knelzap	kvelzap	kzapkur
Эталон	2829	2574	25	271	19	177	94
9 . mm	2263,2	2059,2	20	216	15,2	141,6	75,2
9 max	3394,8	3088,8	30	325,2	22,8	212,4	112,8
СВЮпо P3	2804	2563	30	258	22	155	103

Таблица 12.1. Эксперимент №12. Случайные величины

	и	cq m о	и	чГ m и	in PP О	40 U	m и	ос pa и	04 n О	О 1-H ca и	s и	cq 2 и	m и	и	irj ^н ра и	СО сч to и
Эталон	2828	5	5	5	2664	267	195	94	18	90	5	72	68	2577	2574	2829
9 . mm	2262	4	4	4	2131	214	156	75	14	72	4	58	54	2062	2059	2263
9 max	3394	6	6	6	3197	320	234	113	22	108	6	86	82	3092	3089	3395
CBH по P3	2905	9	9	9	2729	218	155	86	17	85	И	52	52	2604	2604	2908

Таблица 12.2. Эксперимент №12. Выходные данные СИМ-модели

	kpost	kokaz	kotk	kzapogv	knelzap	kvelzap	kzapkur
Эталон	2829	2574	25	271	19	177	94
э тт	2263	2059	20	216	15	142	75
9 max	3395	3089	30	325	23	212	113
СВ11 по РЗ	2908	2604	26	229	12	143	86

Эксперимент №12. По РЗ изменялась СВ 11 СВ9, СВ 10, СВ 14, СВ 15, СВ23 и отклонения (см. таблицу 12.1). В допустимый интервал во- 6 из 7 переменных: kpost, kokaz, kotk, kzapogv, шли отклонения 8 из 15 СВ: СВ1, СВ5, СВ6, СВ8, kvelzap, kzapkur. (см. таблицу 12.2).

Таблица 13.1. Эксперимент №13. Случайные величины

	во и	сч И и	m и	m и	Ш ВО о	40 СО и	m и	00 60 и	04 ВО и	о М и	m и	еч М и	м ВО и	и	ш и	m гч СО и
Эталон	2828	5	5	5	2664	267	195	94	18	90	5	72	68	2577	2574	2829
тт	2262	4	4	4	2131	214	156	75	14	72	4	58	54	2062	2059	2263
э -'max	3394	6	6	6	3197	320	234	113	22	108	6	86	82	3092	3089	3395
СВ12 по РЗ	2857	9	9	9	2690	233	155	104	20	95	10	65	65	2547	2547	2858

Таблица 13.2. Эксперимент №13. Выходные данные СИМ-модели

	kpost	kokaz	kotk	kzapogv	knelzap	kvelzap	kzapkur
Эталон	2829	2574	25	271	19	177	94
9 . —'тт	2263	2059	20	216	15	142	75
9 ^х-'тах	3395	3089	30	325	23	212	113
СВ12 по РЗ	2858	2547	29	243	16	139	104

Таблица 14.1. Эксперимент №14. Случайные величины

	rH # и	СЧ m и	m и	m и	in BO U	40 m и	m о	oo m о	04 m о	о m и	m и	гч m и	m и	тТ ВО о	ш ВО о	гч М О
Эталон	2828	5	5	5	2664	267	195	94	18	90	5	72	68	2577	2574	2829
9 . mm	2263	4	4	4	2131	214	156	75	14	72	4	58	54	2062	2059	2263
э —'max	3394	6	6	6	3197	320	234	113	22	108	6	86	82	3092	3089	3395
CB13 по P3	2918	9	9	9	2733	194	139	74	14	65	7	43	43	2617	2617	2920

Таблица 14.2. Эксперимент №14. Выходные данные СИМ-модели

	kpost	kokaz	kotk	kzapogv	knelzap	kvelzap	kzapkur
Эталон	2829	2574	25	271	19	177	94
9 . —'тт	2263	2059	20	216	15	142	75
9 —' max	3395	3089	30	325	23	212	113
СВ13по РЗ	2920	2617	28	197	12	127	74

Таблица 15.1. Эксперимент №15. Случайные величины

	м и	ГЦ М и	ГГ> м и	-* м и	1Л М и	че М и	и	00 М и	ОЧ М и	о и	m и	eq i-н Ю и	m и	■у и	ID 2 и	ГО eq СО U
Эталон	2828	5	5	5	2664	267	195	94	18	90	5	72	68	2577	2574	2829
тт	2262	4	4	4	2131	214	156	75	14	72	4	58	54	2062	2059	226
э max	3394	6	6	6	3197	320	234	113	22	108	6	86	82	309	3089	3395
СВ14 по РЗ	2857	6	6	6	2688	261	184	105	21	105	8	82	82	2570	2570	2858

Таблица 15.2. Эксперимент №15. Выходные данные СИМ-модели

	kpost	kokaz	kotk	kzapogv	knelzap	kvelzap	kzapkur
Эталон	2829	2574	25	271	19	177	94
min	2263,2	2059,2	20	216	15,2	141,6	75,2
э max	3394,8	3088,8	30	325,2	22,8	212,4	112,8
СВ 14 по РЗ	2858	2570	25	269	20	164	105

Таблица 16.1. Эксперимент №16. Случайные величины

	и	СЦ m и	2 и	it и	К) m и	40 m и	m о	ос m и	04 m и	о m о	m и	г 1 m и	m и	m и	in и	го eq CO и
Эталон	2828	5	5	5	2664	267	195	94	18	90	5	72	68	2577	2574	2829
'-'min	2262	4	4	4	2131	214	156	75	14	72	4	58	54	2062	2059	2263
Э max	3394	6	6	6	3197	320	234	ИЗ	22	108	6	86	82	3092	3089	3395
CB15 по P3	2804	6	6	6	2655	228	163	92	18	85	7	68	67	2590	2590	2808

Таблица 16.2. Эксперимент №16. Выходные данные СИМ-модели

	kpost	kokaz	kotk	kzapogv	knelzap	kvelzap	kzapkur
Эталон	2829	2574	25	271	19	177	94
'-'mm	2263,2	2059,2	20	216	15,2	141,6	75,2
max	3394,8	3088,8	30	325,2	22,8	212,4	112,8
CB15поP3	2808	2590	29	232	20	143	92

Таблица 17. Число СВ, не вошедших в допустимый интервал, при изменении закона распределения фиксированной СВ на равномерный

св_п	СВ1	CB2	свз	CB4	CB5	СВб	СВ7	СВ8	СВ9	СВ10	СВ11	CB12	CB13	СВ 14	CB15
Ncb	4	3	4	0	1	4	4	7	9	4	8	7	15	2	1

Таблица 18. Число прогонов, в которых значения СВ не входили в допустимый интервал ±20%

св„	СВ1	CB2	свз	CB4	CB5	СВб	СВ7	СВ8	СВ9	свю	СВ11	CB12	CB13	CB14	CB15	CB23
N_Cb	0	10	10	10	0	3	6	1	1	3	10	4	5	0	0	0

Таблица 19. Итоговые результаты исследования тестовой СИМ-модели

	kpost	kokaz	kotk	kzapogv	knelzap	kvelzap	kzapkur
Эталон	2829	2574	25	271	19	177	94
mm	2263	2059	20	216	15	142	75
	3395	3089	30	325	23	212	113
Все по P3 (№ 1)	2698	2270	28	224	29	127	97
CB1 по P3 (№2)	2447	2181	21	250	21	143	108
CB2 по P3 (№3)	2822	2579	25	266	19	175	91
СВЗ по P3 (№4)	2710	2487	23	250	15	165	87
CB4 по P3 (№5)	2829	2574	25	271	19	177	94
CBS по P3 (№6)	2829	2561	30	266	20	178	88
СВб по P3 (№7)	2843	2568	34	239	20	144	95
CB7 по P3 (№8)	2794	2531	23	210	16	122	88
CBS по P3 (№9)	2822	2549	26	226	15	134	93
CB9 по P3 (№10)	2754	2486	30	206	9	129	77
CB10 по P3 (№11)	2804	2563	30	258	22	155	103
CB11 по P3 (№12)	2908	2604	26	229	12	143	86
CB12 по P3 (№13)	2858	2547	29	243	16	139	104
CB13 по P3 (№14)	2920	2617	28	197	12	127	74
CB14 по P3 (№15)	2858	2570	25	269	20	164	105
CB15 по P3 (№16)	2808	2590	29	232	20	143	92

В экспериментах №2, №3, №5, №6, №11, № 15, №16 все 7 переменных вошли в допустимый интервал отклонения в 20%.

Заключение

Изменение закона распределения случайных величин СВ1 «Длительность приема документов», СВ2 «Время ожидания недостающих документов», СВ4 «Длительно сть анализа КД регистратором», СВ5 «Длительность анализа поступившего дела», СВ 10 «Длительность анализа КД в ОГВ», СВ14 «Время ожидания заявителя», СВ15 «Время выдачи результата услуги заявителю» не влияет на итоговые значения СИМ-модели и в меньшей степени влияет на значения других СВ, поэтому можно считать, что данные СВ обусловлены второстепенными статистическими факторами.

Список литературы Влияние неопределенности исходных данных на эффективность статистического имитационного моделирования нерефлекторной системы. Часть 2. Дифференциация стохастических факторов по влиянию на эффективность применения СИМ-модели

Ваулина К.В., Маслов О.Н. Влияние неопределенности исходных данных на эффективность статистического имитационного моделирования нерефлекторной системы. Часть 1.Тестовая СИМ-модель//ИКТ. Т.14, №3, 2016. -С. 132-139
Димов Э.М., Маслов О.Н., Пчеляков С.Н., Скворцов А.Б. Новые информационные технологии: подготовка кадров и обучение персонала. Часть 2. Имитационное моделирование и управление бизнес-процессами в инфокоммуникациях. Самара: Изд-во СНЦ РАН, 2008. -350 с.
Ануфриев Д.П., Димов Э.М., Маслов О.Н. и др. Статистическое имитационное моделирование и управление бизнес-процессами в социально-экономических системах. Астрахань: Изд-во АстИСИ, 2015. -366 с.
Димов Э.М., Маслов О.Н., Трошин Ю.В. Снижение неопределенности выбора управленческих решений с помощью метода статистического имитационного моделирования//Информационные технологии. №6, 2014. -С. 51-57.

Статья научная