Влияние околоскважинных зон на продуктивность газовых скважин

С ростом энергетических затрат России и возрастающим спросом на мировом рынке энергоресурсов возникает необходимость увеличения темпов добычи углеводородов. Большинство месторождений России относится к категории месторождений с трудно извлекаемыми запасами или находятся в конечной стадии разработки. Разработка таких месторождений традиционными методами мало эффективна. Создание принципиально новых методов рационального извлечения углеводородов требует более глубокого понимания процессов, происходящих в пласте. В статье проведено исследование влияния околоскважинных зон (ОЗ) на продуктивность газовых скважин и коэффициенты гидродинамического сопротивления (КГС) пласта. Определение КГС является важнейшей задачей, определяющей динамику добычи газа, продуктивность и правильность интерпретации результатов гидродинамических исследований скважин. Существует много факторов, искажающих форму индикаторных кривых и вносящих погрешность в результаты определения КГС. К ним относятся: кольматация ОЗ, деформация пласта вследствие бурения, эффекты защемления газа, несовершенство вскрытия пласта и т.д. Учёт влияния этих процессов в существующих методах стационарной и нестационарной фильтрации газа ранее не производился. Для определения КГС и анализа их изменения вследствие проявления эффектов ухудшения свойств ОЗ авторами создана численная модель фильтрации газа по двучленному закону. На основе этой модели в статье проведено исследование влияния сложно построенных ОЗ на КГС и показано, что процессы ухудшения фильтрационных свойств ОЗ оказывают существенное воздействие на КГС пласта.

II. Фильтрационная модель околоскважинной зоны

В работе фильтрационная модель ОЗ построена на основе двучленного уравнения фильтрации газа:

dp2 dr

+

η · pатм Q

rk (rp) • 2n • h(r)pатм

β · pатмQ2

r 2^ k (r,p)4 n 2 h (r )2ρатм

+

,

с граничными условиями на забое и контуре:

PV=rc = Pc,p|r=rk = Pk,             (2)

где Q — продуктивность скважины, h — эффективная толщина, k — проницаемость флюида, β — параметр, зависящий от структуры порового пространства, ρ _атм — плотность газа при атмосферном давлении, r _c — радиус скважины, r k — радиус контура, η — вязкость. Моделирование процессов, ухудшающих фильтрационные свойства ОЗ, производилось посредством представления функции фазовой проницаемости в виде: k ( r,p ) = k о A ( r ) f ( p ) f н ( r ), где функция A ( r ) моделирует процесс кольматации ОЗ, f ( p ) — влияние сжимаемости породы пласта, f н ( r ) — процесс осушки ОЗ. Несовершенство вскрытия пласта моделировалось введением зависимости эффективной толщины пласта от радиуса h ( r ). Влияние каждого из этих факторов на КГС рассмотрено в следующих пунктах статьи.

III. Кольматация околоскважиннойзоны

В случае, когда пласт не подвержен техногенным изменениям k ( r,p ) = k о , уравнение фильтрации (1) легко решается аналитически и приводится к виду (3). Индикаторная кривая спрямляется в координатах Д p ² /Q = f (Q) и КГС. A 0 , B 0 определяются стандартным образом по формулам (4)

и (5):
Р к - Р 2 = Q • A 0	+ Q 2 • B 0 ,	(3)
A =    ПР атм    ln Г к 2 nHk 0 р атм    Г с		(4)
B   ____ вР атм ____ / 1     1 A 0    4 П 2 H 2 Vk 0 P атм \ Г с Гк)		(5)

подход к определению A ( г ) является более обоснованным. На рис. 1 показано сравнение предлагаемого профиля с использовавшимися ранее. Очевидно существенное отличие между ними, отражающееся на КГС.

В процессе бурения частицы шлама вместе с буровым раствором проникают в околоскважинное пространство, ухудшая фильтрационные свойства коллектора, и, как следствие, оказывают влияние на КГС. В работе влияние процессов засорения моделировалось введением функции A ( г ) в формулу для коэффициента фазовой проницаемости газа. В этом случае уравнение фильтрации (1) также разрешается аналитически и определяются КГС через соответствующие интегральные функции (6) и (7), где r _п р — радиус зоны проникновения фильтрата бурового раствора. Кроме того, определяются коэффициенты добавочного сопротивления S _a , S b , характеризующие степень коль-матации околоскважинной зоны (8--9):

r _пр

dr

ф(rc,rпр) = J rAr,            (6)

r c

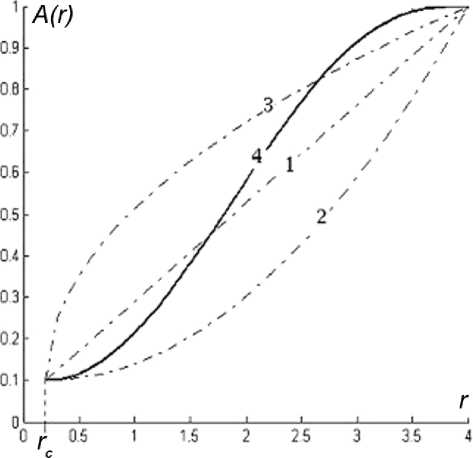
Рис. 1. Сравнение различных A ( r ) ; 1 — линейная, 2 — квадратичная, 3 — корневая, 4 — полученная из ГИС

A

B =

r пр

ф( rc,r пр) =

r rc

ηp атм

^{2 n}Hk 0 ^р атм

dr

(Ф(Гс ,Гпр

r k

) + ln--- rпр

)

ηp атм

2 nHk о р атм

(l° rk+Sa),

βp атм

4 П ² H ² Vk o P атм

(^{ф( Г с ,Г п}р ) ⁺ г пр - £) =

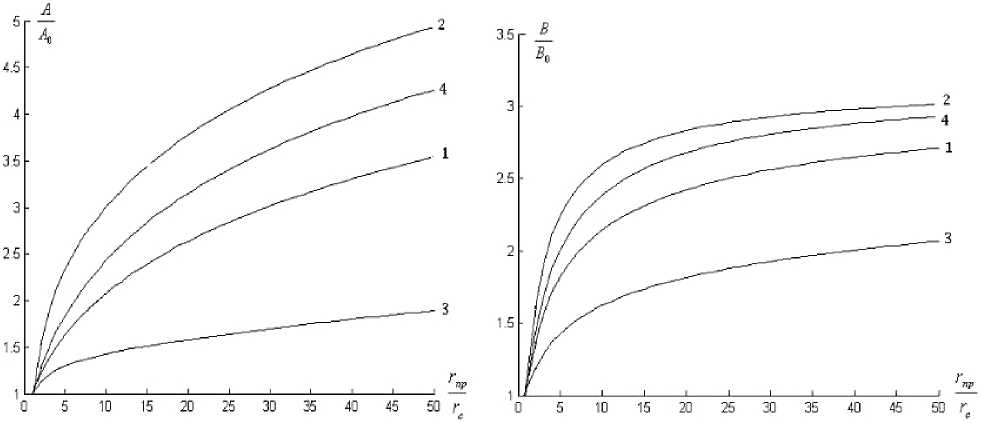
В работе построены зависимости относительных (загрязнённый / чистый) КГС и добавочных КГС от радиуса зоны кольматации для различных видов радиальной функции засорения A ( г ), представленных на рис. 1. Из рис. 2 и 3 видно, что вид зависимости A ( г ) существенно влияет как на относительные КГС, так и на добавочные КГС. Поэтому корректное определение радиального профиля засорения является важнейшей задачей.

IV. Влияние несовершенства вскрытия пласта по толщине

_____вРатм_____ /1 rc + s 4 П 2 H2 VkoP атм Гс \    rk    Ь,

Sa = Ф(Гс,Гпр) + ln -rk- - ln rk ,

Sb = Гс • ф(Гс,гпр) + — - 1.        (9)

r пр

Из экспериментальных исследований известно [1], что проницаемость ОЗ зависит от расстояния до скважины, и эта зависимость имеет вид кривой выпуклой к оси проницаемости. В работе влияние процессов засорения моделировалось введением функции A ( г ) в формулу для коэффициента фазовой проницаемости газа. Ранее радиальная зависимость проницаемости ОЗ рассматривалась в виде ступенчатой функции или в виде степенной с показателем (1; 2; 1 / 2) [2]. Нами же предлагается использовать функцию A ( г ), полученную из данных каротажа при помощи усреднения методом вероятностных сверток [3]. Такой

Влияние несовершенства вскрытия пласта по толщине моделировалось введением радиальной зависимости эффективной толщины h ( г ), которая была выведена из анализа изменения линий тока в ОЗ [4]. Расчёты показывают, что несовершенство скважины не сказывается на форме линии тока на расстоянии г >  (0 , 5-1 , 0) H , где H — толщина пласта. В зоне r, где сказывается несовершенство скважины, форма линий тока принимается такой, какой она была бы в пласте переменной мощности h(г), которая меняется по степенному закону h (г) = е + xrn, где коэффициенты е и х определяются из граничных условий на подошве пласта и на забое скважины.

Аналогично п. 2 аналитически решается фильтрационное уравнение для несовершенного по глубине вскрытия пласта при помощи введения интегральных функций (10) и (11), где z — толщина зоны перфорации, L — характерное расстояние, на котором происходит искривление линий тока. Так- же определяются КГС и добавочные КГС, характеризующие несовершенство пласта по глубине вскрыти для различных форм линий тока (12,13):

L

^вр атм       / 1    ^r c +

4 n ² H ² V^ o P атм r c X     r k

C b C a

Ф * (rc ,L,z) = | rc

dr rh(r)

= H • Ф* (rc,L,z) + ln L

in rk, rc

L

Ф * (rc ,L,z) = | rc

dr

r2h(r)2 ,

Cb = H2rc • Ф*(rc,L,z) + Lc - 1.

A = np атм (ф * (,   ) + £in rk)

2nk0pатм (   ( c, , ) H    L )

ηp атм

^{2 n}k о H^p атм

(ln rc + £,

B =   вратм--- /Ф* (rc,L,z) + 1 Л

4 П ² Vk o P атм V             H 2 X L

s )=

В работе построены зависимости относительных и добавочных КГС от толщины зоны перфорации (рис. 4, 5) для различных значений показателя n , определяющего кривизну линии тока. Из графиков видно, что форма линий тока в ОЗ и толщина зоны перфорации оказывают существенное влияние как на относительные, так и добавочные КГС.

зоны кольматации для различных A ( r )

Рис. 2. Зависимости относительных КГС от радиуса

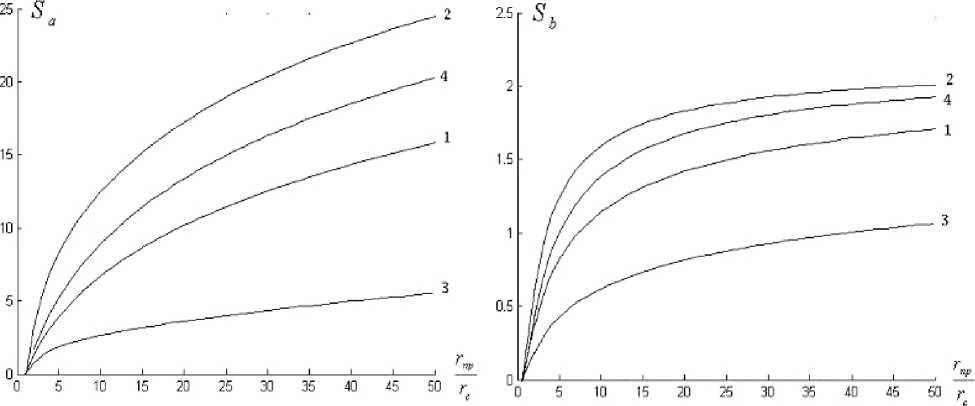
Рис. 3. Зависимости добавочных КГС от радиуса зоны кольматации для различных A ( r )

V. Влияние сжимаемости пласта

Влияние сжимаемости породы пласта моделировалось посредством введения функции f ( р ) в

формулу фазовой проницаемости газа. Опытные данные показывают, что графики зависимости проницаемости от давления имеют вид кривых, выпуклых к оси к ( р ) /к о . Для этих кривых можно подобрать различные аналитические представле-

ния. Наиболее употребительной зависимостью является зависимость вида: к/ко = exp(—а(pk — p)), где p и pk текущее давление и давление на контуре, α — коэффициент изменения проницаемости (МПа-1). Для чисто гранулярных пластов используют зависимость k(p)/ко = (p/pk)7, где γ — безразмерный коэффициент изменения проницаемости пласта. Для чисто трещинного типа пористости был установлен следующий вид зависимости проницаемости от давления: к (p)/к0 = (1 + BLn(p/pk))3, где B — безразмерный коэффициент изменения проницаемости пласта.

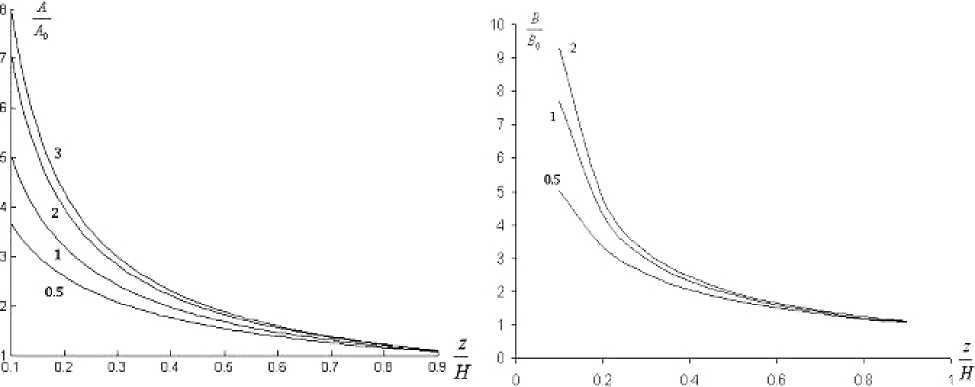
Рис. 4. Зависимости относительных КГС от толщины зоны перфорации для различных n

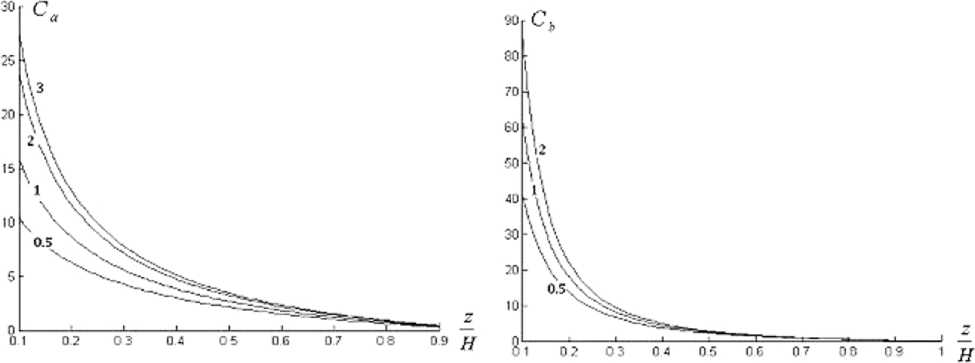
Рис. 5. Зависимости добавочных КГС от толщины зоны перфорации для различных n

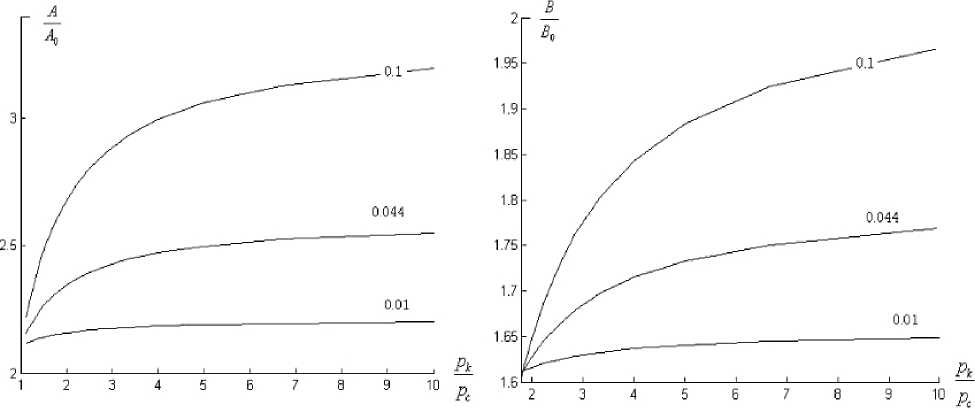
Рис. 6. Зависимости относительных КГС для различных коэффициентов сжимаемости

В случае сжимаемого пласта проницаемость является функцией давления, при этом уравнение фильтрации (1) не имеет аналитического решения в общем виде. Индикаторные кривые в этом случае оказываются выпуклыми к оси дебитов как в координатах Q (Дp2), так и в Дp2/Q = f (Q). Следовательно, для определения КГС необходимо использовать приближённые методы [5]. В случае, когда имеется некоторый набор данных по проницаемости от давления, применяется метод обычного среднеарифметического усреднения. Ho в случае, когда существует функциональная зависимость к (p), необходимо использовать интегральное усреднение. При этом уравнение фильтрации (1) переходит в уравнение (6), из которого определяются промежуточные КГС A∗ и B∗. После чего, зная функцию проницаемости от давления, определяем искомые КГС A и B (15, 16):

2    2            ηp атм        r k

^Pk p c” ^Q' 2 nHp атм kp ^П Г с

I q 2______ ^вр атм _______ / ¹    _1_

4 П ² H ² p атм ^ k ( P ) V c    r k

A ^∗

ПР атм _1n r k _; A = A *

2 nHp атм    Г с          k ( p ) ’

B ^∗

ep атм  ( 1 _O _p    B *

4 П ² H ² p атм ^ Г с    Гк) ^     ^ k ( p ) • ^{( 6)}

В работе проведена обработка индикаторных кри- вых вышеизложенным методом при различных коэффициентах сжимаемости и для различных типов коллекторов. Построены графики зависимостей КГС от приведённого давления (рис. 6, 7), из которых видно, что тип коллектора и значение коэффициента сжимаемости оказывают сильное влияние на КГС.

• VI.    Влияние защемления флюида

Промывка газового пласта обуславливает формирование остаточной промывочной водонасы-щенности (ОПВН) в окрестности добывающей скважины. Традиционно ОПВН считалась фиксированной величиной, зависящей от коллекторских свойств пласта [6]. В то же время анализ состояния остаточной воды в промытых пластах показал, что в гидрофильных пластах ОПВН зависит от гидродинамических условий вытеснения, то есть от капиллярного числа Nc = к ф Дp/ (oL). При изменении отношения гидродинамического градиента давления к капиллярному происходит последовательная смена режимов вытеснения флюида. Радиальный профиль фазовой проницаемости f н (г), учитывающий уменьшение ОПВН в процессе осушки ОЗ, выражается степенной зависимостью (9), где (r1 ; rd) — интервал, в котором происходит капиллярно-напорный режим вытеснения:

f н ^{( Г} ) =

f 1 , BN ^δc , f 2 ,

r1,

Г 1 < Г < r d ,       (17)

r>r d .

Как и в случае сжимаемого пласта, при осушке ОЗ уравнение фильтрации не имеет аналитического решения. Поэтому в работе был подобран численный метод и реализован механизм определения радиуса r 1 при заданном r d . Индикаторные кривые при различных степенях градиента δ ,по-строенные в координатах Д p ² /Q = f (Q), выпуклы к оси дебитов, поэтому, как и при учете сжимаемости, необходимо использовать приближённый метод определения КГС. Используемый для этого интегральный метод усреднения аналогичен методу, используемому в п. 4 с той лишь разницей, что производилось усреднение градиента давления.

В работе проведена обработка индикаторных кривых при различных значениях показателя степени градиента. Построены графики зависимостей КГС от приведённого давления. Из представленных на рис. 8 графиков видно, что процесс осушки ОЗ существенно влияет на КГС.

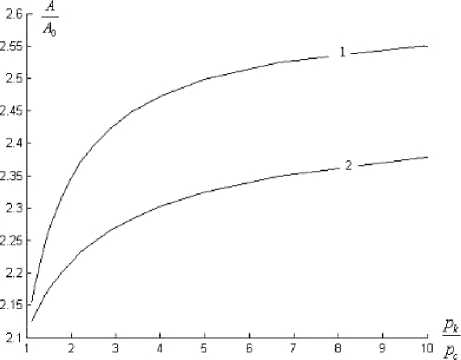
Рис. 7. Зависимости относительных КГС для различных типов коллекторов

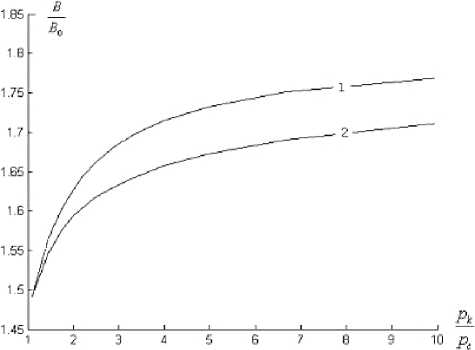
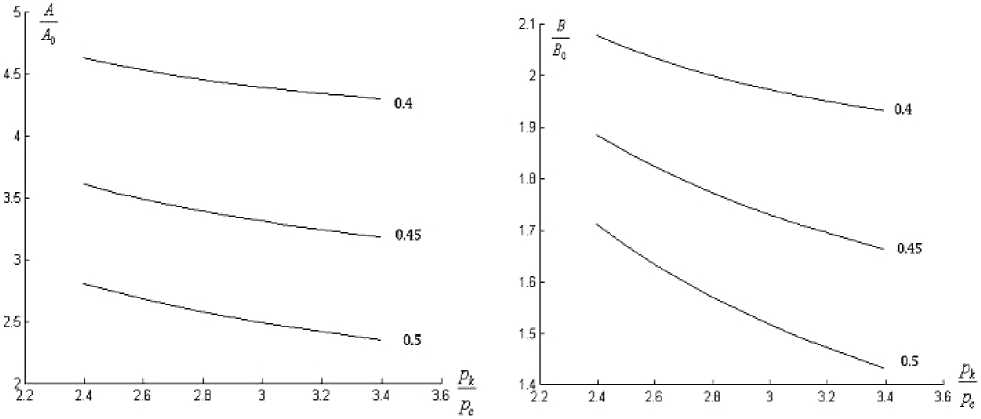
Рис. 8. Зависимости КГС для различных степеней градиента давления; 1 — гранулярный, 2 — трещинный

VII.    Выводы

• 1.    Решена задача о радиальном притоке газа к вертикальной скважине с техногенно изменённой ОЗ.

• 2.    Получены аналитические представления КГС для загрязнённого и несовершенно вскрытого по толщине пласта.

• 3.    Предложена схема определения КГС с помощью методов интегрального усреднения при различных механизмах поражения пласта.

• 4.    Построены зависимости КГС от определяющих параметров, из которых видно, что процессы техногенного изменения ОЗ оказывают значительное воздействие на КГС пласта.