Влияние основных параметров измельчителя толстостебельных культур на мощность
Автор: Фокеев Александр Константинович, Будашов Игорь Александрович
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Технические науки
Статья в выпуске: 7 (58) т.11, 2011 года.
Бесплатный доступ
Приведена конструктивная схема ротационно-дискового измельчающего аппарата, предназначенного для измельчения толстостебельных культур. Предложены формулы для вычисления потребляемой энергии при подпорном и бесподпорном измельчении.
Мощность, измельчение, толстостебельные культуры, ножи
Короткий адрес: https://sciup.org/14249641
IDR: 14249641 | УДК: 631.3.022
Текст научной статьи Влияние основных параметров измельчителя толстостебельных культур на мощность
Введение. Анализ существующих ротационно-дисковых измельчителей и их элементов показал многообразие конструкций, обладающих большим количеством достоинств, но и рядом недостатков. Первый этап работы позволил определить, что ротационно-дисковый измельчитель должен быть :
– с шарнирно подвешенными ножами, способными при перегрузках отклоняться от радиального положения;
– с гребнеобразным ножом-рассекателем;
– с формой ножа, исключающей случайный выход материала из зоны резания и обеспечивающей затягивание стеблей в эту зону;
– с механизмом, ускоряющим возврат державки с ножом в рабочее положение.
Исследование дискового измельчающего аппарата. Аппарат (рис.1) состоит из диска 1, установленного на вертикальном валу 2. На корпусе установлены упругие буферы 3 и зафиксированы державки 4. Ножи 5 крепятся посредством прижатия их к державке 4 втулкой, имеющей конусообразный бурт. Пружина 6, соединяющая державки, ускоряет их возврат в рабочее положение. Под зоной действия ножей установлен гребнеобразный нож-рассекатель 7.
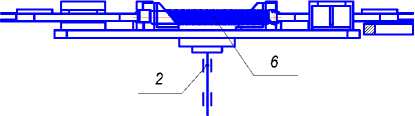
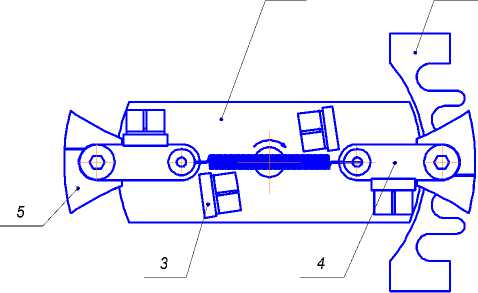
Рис.1. Схема дискового измельчающего аппарата
Затраты энергии, расходуемые измельчителем при работе, изучены недостаточно. Большинство исследований посвящено аппаратам барабанного типа. В связи с этим возникает задача изучения этих затрат для дискового измельчителя.
В процессе решения этой задачи нами были выведены формулы, отражающие зависимость потребляемой мощности резания от основных конструктивных и кинематических параметров измельчителя. Для более детального изучения процесса в аппарате использовали три вида ножей: с прямой формой лезвия, с криволинейной и с криволинейной формой, имеющей насечку.
Потребляемую мощность (Вт) бесподпорного резания для прямого и криволинейного лезвия вычисляют по формуле:
1,(6) -б- 5 -с р - Н 3 + 0,00078 f - E -п- d 4 - cos [ arctg ( k - tg т ) ]- cos3 у- K - n - cos a
Npe3 = K - n - cos a-H3 X xr - cos т- п- n (1 + k - tg2т), где δ – толщина (острота) лезвия, м; s – подача, м/с; σр – нормальные (контактные) разрушающие напряжения, возникающие в перерезаемом стебле, Н/м2; Н – высота резания, м; f – стрела прогиба стебля, м; Е – модуль упругости стебля при растяжении, Н/м2; d – диаметр стебля, м; k=0,325 – коэффициент пропорциональности [1]; τ – угол скольжения, град.; γ – угол отклонения от вертикали по направлению подачи, град.; К – число ножей; n – число оборотов диска с ножами в минуту; α – угол между кромкой лезвия ножа и направлением подачи стеблей при наиболее нагруженной позиции активной части лезвия, град.; r – радиус-вектор, равный расстоянию от оси вращения вала с ножами до точки приложения критической силы на стебле, м.
Потребляемую мощность (Вт) бесподпорного резания для лезвия с насечкой вычисляют по формуле:
1,95 -6- 5 -с р - Н 3 + 0,00078 f - E -п- d 4 - cos [ arctg ( k - tg т ) ]- cos3 y- K - n - cos a
Npe3 = K - n - cos a-H3 X xr - cos т-п- n (1 + k - tg 2т).
Потребляемую мощность (Вт) подпорного резания для прямого и криволинейного лезвия, вычисляют по формуле:
16006 - 5 - ср - а(Н + а) + 0 - E - п - d4 - cos [arctg (k - tgт)] • cos2 у - K - n - cos a рез 480К - n - cos a- а (Н + а)
xr - cos т-п- n (1 + k - tg2 т), где а – зазор между подвижным и неподвижным ножом, м; Θ=0,001 – угол поворота стебля в плоскости среза, рад.
Потребляемую мощность (Вт) подпорного резания для лезвия с насечкой вычисляют по формуле:
1872 6- 5 -с р - а ( Н + а ) + 0 - E - п - d 4 - cos [ arctg ( k - tg т ) ] • cos2 у - K - n - cos a рез 480 К - n - cos a- а ( Н + а )
x r - cos т-п- n ( 1 + k - tg 2 т ) .
Целью нашего исследования является получение математического описания процесса измельчения лезвием, то есть получение зависимости между потребляемой мощностью процесса и принятыми независимыми факторами. В качестве математической модели процесса для подсолнечника и кукурузы может быть принята функция:
Nрез = f(Pr, s, Lл, n, γ), для кустарниковой поросли клёна диаметром до 40 мм:
N рез = ЛPr , 5 , L л , n , Y, d .
Результаты выбора факторов для подсолнечника, кукурузы и области их исследования представлены в табл.1.
Таблица 1
Факторы, интервалы и уровни их варьирования в экспериментах по описанию области оптимума для подсолнечника и кукурузы
|
Факторы |
X о О о Ю 1-о X CD S о т 8 ¥ |
Уровни реального значения факторов |
Интервал варьирования факторов, ε |
со о о га ■& о ^ |
Уровни кодированного значения факторов |
||||
|
ЭХ О CD О X о |
X X си со |
1 |
эх О X со о X о |
X X си со |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Принцип среза |
Pr |
подпорный |
– |
бесподпорный |
– |
x 1 |
–1 |
– |
+1 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Подача, м/с |
s |
0,4 |
0,6 |
0,8 |
0,2 |
x 2 |
–1 |
0 |
+1 |
|
Форма линии лезвия ножа |
L л |
прямая |
радиусная |
с насечкой |
– |
x 3 |
–1 |
0 |
+1 |
|
Частота вращения диска, мин–1 |
n |
1200 |
1400 |
1500 |
200 |
x 4 |
–1 |
0 |
+0,5 |
|
Отклонение стебля от вертикали, град. |
Y |
0 |
14 |
28 |
14 |
x 5 |
–1 |
0 |
+1 |
Результаты выбора факторов для измельчения кустарников клёна и области их исследования представлены в табл.2.
Таблица 2
Факторы, интервалы и уровни их варьирования в экспериментах по описанию области оптимума для кустарниковой поросли клёна
|
Факторы |
X о О о Ю 1-о X CD S о т |
Уровни реального значения факторов |
Интервал варьирования факторов, ε |
со о о га ■& о |
Уровни кодированного значения факторов |
||||
|
ЭХ О X о X о |
X X си со |
1 |
эх О X о X о |
X X си со |
|||||
|
Принцип среза |
Pr |
подпорный |
– |
бесподпорный |
– |
x 1 |
–1 |
– |
+1 |
|
Подача, м/с |
s |
0,4 |
0,6 |
0,8 |
0,2 |
x 2 |
–1 |
0 |
+1 |
|
Форма линии лезвия ножа |
L л |
прямая |
радиусная |
с насечкой |
– |
x 3 |
–1 |
0 |
+1 |
|
Частота вращения диска, мин 1 |
n |
1200 |
1400 |
1500 |
200 |
x 4 |
–1 |
0 |
+0,5 |
|
Отклонение стебля от вертикали, град. |
Y |
0 |
14 |
28 |
14 |
x 5 |
–1 |
0 |
+1 |
|
Диаметр стебля, мм |
d |
20 |
30 |
40 |
10 |
х 6 |
–1 |
0 |
+1 |
Оптимизацию параметров ротационно-дискового измельчающего аппарата проводили методом планирования эксперимента. Для отыскания оптимального сочетания выделенных факторов, дающего минимальную величину потребляемой энергии, были проведены полные факторные эксперименты типа 25 – для стеблей подсолнечника и кукурузы и 26 – для кустарниковой поросли клёна.
Фактор х 6 принят только для кустарника клёна, так как стебли кукурузы диаметром 25 мм и стебли подсолнечника диаметром 23 мм приняты за эталон.
Количество повторностей измерений определяется следующими величинами : доверительная вероятность а = 0,95 ; допустимая ошибка измерений, выраженная в долях среднеквадратического отклонения σ равна ε = ± 3 σ . В зависимости от выбранных значений количество повторностей опытов будет равно 3 [6].
Перед проведением основных опытов нужно убедиться, что опыты воспроизводимы. Для каждой серии параллельных опытов вычисляется среднее арифметическое значение функции отклика:
m уu= 1 ∑yi′u , (u =1, 2, …, N), m i=1
где m – число повторностей (число измерений).
Затем вычисляется оценка дисперсии для каждой серии параллельных опытов:
m
σ i 2 = ∑ ( yi ′ u - yu ) 2 .
m - 1 i = 1
Дисперсионный анализ экспериментальных данных можно проводить при условии однородности дисперсии опытов. Так как число опытов в каждой строке плана одинаково, то для проверки гипотезы об однородности применен критерий Кохрена.
Для проверки воспроизводимости опытов найдём отношение наибольшей из дисперсий к сумме всех дисперсий [3]:
σ 2
σ i max
Gоп = N ,
∑ σ i 2
i = 1
где G оп – расчётное значение критерия Кохрена.
Для нахождения табличного значения Кохрена G задаёмся доверительной вероятностью, с которой принимается гипотеза о воспроизводимости опытов Р = 0,95 [7].
Табличное значение критерия Кохрена G для стеблей кукурузы и подсолнечника при N =32 и f =2 оказалось равным 0,18892, а для кустарниковой поросли клёна при N =41 и f =2 равным 0,2338 [3].
Основные результаты расчета воспроизводимости опытов приведены в табл.3.
Проверка однородности дисперсий
Таблица 3
|
Выходной параметр |
S 2 y max |
G оп |
G таб |
Однородность дисперсии |
|
Критерий оптимизации: у 1 |
0,04 |
0,0802 |
0,1889 |
да |
|
у 2 |
0,04 |
0,0847 |
0,1889 |
да |
|
у 3 |
0,04 |
0,0786 |
0,2338 |
да |
Результаты проверки значимости коэффициентов регрессии с учётом дисперсий параметров сведены в табл.4.
Таблица 4
Расчёт доверительного интервала
|
Выходной параметр |
Sb i |
±∆b i |
|
Критерий оптимизации: у 1 |
0,016 |
0,0314 |
|
у 2 |
0,015 |
0,0298 |
|
у 3 |
0,012 |
0,0243 |
Для проверки адекватности представления результатов эксперимента полиномом первой степени определяли расчётное значение критерия Фишера [2]. Результаты проверки адекватности моделей для всех параметров y 1 , y 2 и y 3 приведены в табл.5.
Таблица 5 Проверка адекватности линейного приближения
|
Выходной параметр |
2 S LF |
S y 2 |
F рас |
F , таб |
Подтверждение адекватности |
|
Критерий оптимизации: у 1 |
0,0266 |
0,016 |
1,6618 |
1,7 |
нет |
|
у 2 |
0,0231 |
0,015 |
1,5376 |
1,7 |
нет |
|
у 3 |
0,0185 |
0,012 |
1,5407 |
1,56 |
нет |
Адекватность линейной модели также проверялась по гипотезе о равенстве нулю (нуль-гипотезе) [3] суммы коэффициентов при квадратичных членах. Результаты адекватности с проверкой по критерию Стьюдента ( t -критерию) показаны в табл.6.
Таблица 6 Проверка адекватности модели по нуль-гипотезе
|
Выходной параметр |
t рас |
t таб |
Адекватность линейной модели |
|
Критерий оптимизации: у 1 |
1,9989 |
2,001 |
да |
|
у 2 |
1,9991 |
2,001 |
да |
|
у 3 |
2,005 |
2,007 |
да |
После проведения испытаний, обработки полученных данных и перехода от кодированных значений к натуральным нами получены следующие математические модели:
– для подсолнечника
N рез = –8,853+0,888 Pr +22,807 s +0,397 L л +0,006655 n –0,05385714γ+0,78× Pr × s – –0,144 Pr × L л –0,000625 Pr × n +0,28 L л × s –0,01485 s × n +0,0425 s ×γ–0,00019 L л × n +0,00001357 n ×γ;
– для кукурузы
N рез = 0,638+0,755 Pr +5,875 s +0,224 L л –0,000135 n –0,04828571γ+0,69× Pr × s – –0,113× Pr × L л –0,000545 Pr × n +0,19 L л × s –0,0029 s × n +0,03571429 s ×γ– –0,00017 L л × n +0,00001214 n ×γ;
– для кустарниковой поросли клёна
N рез = 64,079–27,752 Pr –0,035 s +3,037 L л –0,02288 n –0,26221429γ–0,2064 d – –3,195× Pr × s –0,849 Pr × L л +0,003575 Pr × n +0,05435714 Pr ×γ+0,6332 Pr × d +2,49 L л × × s –0,001775 s × n +0,04535714 s ×γ+0,0465 s × d –0,003425 L л × n +0,00764286 L л ×γ+ +0,0098 L л × d +0,00001464 n ×γ+0,000538 n × d +0,00557143γ× d .
После отсеивания малозначащих факторов исследования по описанию поверхности отклика были продолжены методом крутого восхождения (методом Бокса – Уилсона). В соответствии с этим методом нужно определить фактор, наиболее сильно влияющий на критерий оптимизации: единичный шаг λс; расчет произведения коэффициентов регрессии bi и интервала варьирования фактора si. Шаг фактора Xi вычисляют по формуле [4]:
Л = b' Л, i bcεc c где bc , εc – соответственно коэффициент и интервал варьирования «сильного фактора».
Программу крутого восхождения проводим в два потока. Сначала делаем опыты для стеблей подсолнечника и кукурузы, так как алгоритм изменения коэффициентов регрессии у них тождественен, а затем для кустарниковой поросли клёна.
В соответствии с этим методом и соображениями, ранее изложенными, в качестве единичного шага для стеблей подсолнечника и кукурузы было выбрано изменение величины частоты вращения диска ( фактор х 4 ) на 100 м/с. Проведённые ранее эксперименты показали, что принцип среза ( фактор х 1 ) в данном случае нужно зафиксировать как подпорный. Величина единичного шага по другим факторам принималась пропорциональной величине принятого шага фактора х 4 . Так как определялись параметры области оптимума, соответствующие минимальной величине потребляемой энергии, затрачиваемой на резание, то шаговый процесс движения осуществлялся со знаками, соответствующими знакам, замененными на обратные. Результаты крутого восхождения приведены в табл.7.
Таблица 7
Программа крутого восхождения по определению минимальной потребляемой энергии экспериментального измельчающего аппарата ротационно-дискового типа при резании стеблей подсолнечника и кукурузы
|
Обозначение |
Подача, м/с |
Форма линии лезвия ножа |
Частота вращения диска, об/мин |
Отклонение стебля от вертикали, град. |
Критерии оптимизации, кВт |
|
|
x 2 |
х 3 |
х 4 |
х 5 |
y 1 |
y 2 |
|
|
Верхний уровень (+1) |
0,8 |
с насечкой |
1500 |
28 |
||
|
Основной уровень (0) |
0,6 |
радиусная |
1400 |
14 |
||
|
Нижний уровень (–1) |
0,4 |
прямая |
1200 |
0 |
||
|
Коэффициент регрессии b i подсолнечника |
+0,55 6 |
+0,131 |
–0,413 |
–0,131 |
||
|
Коэффициент регрессии b i кукурузы |
+0,46 3 |
+0,1 |
–0,341 |
–0,138 |
||
|
Интервал варьирования факторов ε |
0,2 |
- |
200 |
14 |
||
|
Шаг, соответствующий изменению х 4 на 100 об/мин |
+0,1 |
- |
–100 |
–2,2 – для подсолнечника –2,8 – для кукурузы |
||
|
Округлённый шаг |
+0,1 |
- |
–100 |
–2 |
||
|
Опыт по программе крутого восхождения: |
||||||
|
33 |
0,6 |
радиусная |
1400 |
14 |
1,2 |
1,2 |
|
34 |
0,5 |
прямая |
1500 |
16 |
1 |
1 |
|
35 |
0,4 |
прямая |
1500 |
18 |
0,8 |
0,8 |
|
36 |
0,4 |
прямая |
1500 |
20 |
0,8 |
0,8 |
|
37 |
0,4 |
прямая |
1500 |
22 |
0,8 |
0,8 |
|
38 |
0,4 |
прямая |
1500 |
24 |
0,8 |
0,8 |
|
39 |
0,4 |
прямая |
1500 |
26 |
0,8 |
0,8 |
|
40 |
0,4 |
прямая |
1500 |
28 |
0,8 |
0,8 |
|
41 |
0,4 |
прямая |
1300 |
28 |
0,8 |
0,8 |
|
42 |
0,4 |
радиусная |
1200 |
28 |
0,8 |
0,8 |
Фактор х 4 при реализации второго шага достиг величины, увеличение которой нецелесообразно по рекомендации работы [5], поэтому величина его была зафиксирована и в дальнейших опытах оставалась на оптимальном уровне, соответствующем 1500 об/мин. Фактор х 2 при реализации третьего шага достиг величины, уменьшение которой оказалось экономически нецелесообразным, поэтому величина его была зафиксирована и в дальнейших опытах оставалась на оптимальном уровне, соответствующем наименьшей подаче 0,4 м/с. При достижении восьмого шага фактор х 5 достиг оптимальной величины и был зафиксирован на величине 28°. На этом шаге было принято решение уменьшать частоту вращения диска, так как величина критерия оптимизации одного из проведённых ранее опытов методом планирования эксперимента при n =1200 мин–1 меньше, чем на предыдущих шагах крутого восхождения. На десятом шаге фактор х 3 рассмотрен на основном уровне, так как здесь есть вероятность нахождения области оптимума.
Теперь рассмотрим крутое восхождение для кустарниковой поросли клёна. В качестве единичного шага для поросли клёна было выбрано изменение диаметра стебля ( фактор х 6 ) на 5 мм. Проведённые ранее эксперименты показали, что принцип среза ( фактор х 1 ) в данном случае нужно зафиксировать как бесподпорный. Величина единичного шага по другим факторам принималась пропорциональной величине принятого шага фактора х 6 . Так как определялись параметры области оптимума, соответствующие минимальной величине потребляемой энергии, затрачиваемой на резание, то шаговый процесс движения осуществлялся со знаками, соответствующими знакам, замененными на обратные. Результаты крутого восхождения приведены в табл.8.
Таблица 8
Программа крутого восхождения по определению минимальной потребляемой энергии экспериментального измельчающего аппарата ротационно-дискового типа при резании кустарниковой поросли клёна
|
Обозначение |
Подача, м/с |
Форма линии лезвия ножа |
Частота вращения диска, об/мин |
Отклонение стебля от вертикали, град. |
Диаметр стебля, мм |
Критерий оптимизации, кВт |
|
x 2 |
х 3 |
х 4 |
х 5 |
х 6 |
y 3 |
|
|
Верхний уровень |
0,8 |
с насечкой |
1500 |
28 |
40 |
|
|
Основной уровень (0) |
0,6 |
радиусная |
1400 |
14 |
30 |
|
|
Нижний уровень (–1) |
0,4 |
прямая |
1200 |
0 |
20 |
|
|
Коэффициент регрессии b i |
–0,098 |
+0,137 |
–1,52 |
–0,063 |
–6,527 |
|
|
Интервал варьирования факторов, ε |
0,2 |
– |
200 |
14 |
10 |
|
|
Шаг, соответствующий изменению х 6 на 5 мм |
–0,001 |
– |
–23,3 |
–0,07 |
–5 |
|
|
Округлённый шаг |
–0,1 |
– |
–100 |
–2 |
–5 |
|
|
Опыт по программе крутого восхождения: |
||||||
|
65 |
0,6 |
радиусная |
1400 |
14 |
30 |
2,8 |
|
66 |
0,7 |
прямая |
1500 |
16 |
30 |
2,8 |
|
67 |
0,8 |
прямая |
1500 |
18 |
30 |
3,2 |
|
68 |
0,8 |
прямая |
1500 |
20 |
30 |
3 |
|
69 |
0,8 |
прямая |
1500 |
22 |
30 |
3 |
|
70 |
0,5 |
прямая |
1300 |
24 |
30 |
2,6 |
|
71 |
0,4 |
прямая |
1200 |
26 |
30 |
2,2 |
|
72 |
0,4 |
прямая |
1200 |
28 |
30 |
2,2 |
|
73 |
0,4 |
радиусная |
1200 |
28 |
30 |
2,2 |
|
74 |
0,4 |
прямая |
1200 |
28 |
35 |
2,2 |
|
75 |
0,4 |
прямая |
1200 |
28 |
40 |
2,8 |
|
76 |
0,4 |
прямая |
1200 |
28 |
25 |
1,8 |
При реализации крутого восхождения с первого по девятый шаг фактор х 6 было решено оставить на основном уровне, так как интерес вызывает не только оптимизация потребляемой энергии в интервале диаметров, но и для каждого диаметра в отдельности тоже. На шестом шаге значения факторов х 2 и х 4 было решено заменить с возрастающих на убывающие, так как отклик одного из проведённых ранее опытов методом планирования эксперимента при х 2 =0,4 м/с и х 4 =1200 мин–1 меньше, чем на предыдущих шагах крутого восхождения. На девятом шаге фактор х 3 рассмотрен на основном уровне, так как здесь так же, как и в опытах со стеблями подсолнечника и кукурузы, есть вероятность нахождения области оптимума. На последующих шагах проводились опыты для отыскания оптимума для каждого диаметра с кратностью 5 мм.
Выявлено, что на мощность, затрачиваемую на измельчение резанием подсолнечника и кукурузы при заданных интервалах факторов, основное влияние оказывает подача (рис.2 и 3).
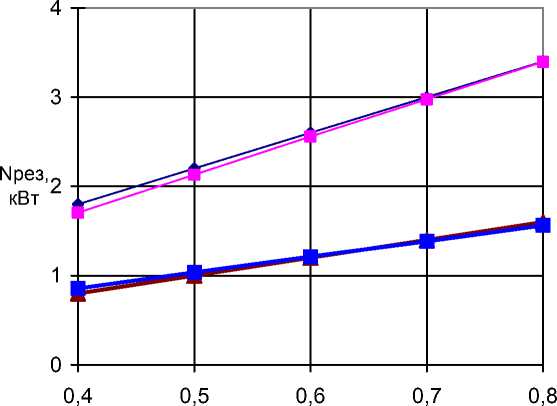
Экспериментальная зависимость при верхнем уровне остальных факторов
Теоретическая зависимость при верхнем уровне остальных факторов
—*—Экспериментальная зависимость при нижнем уровне остальных факторов
—■—Теоретическая зависимость при нижнем уровне остальных факторов s, м/с
Рис.2. Зависимость потребляемой мощности на резание подсолнечника от подачи режущего аппарата
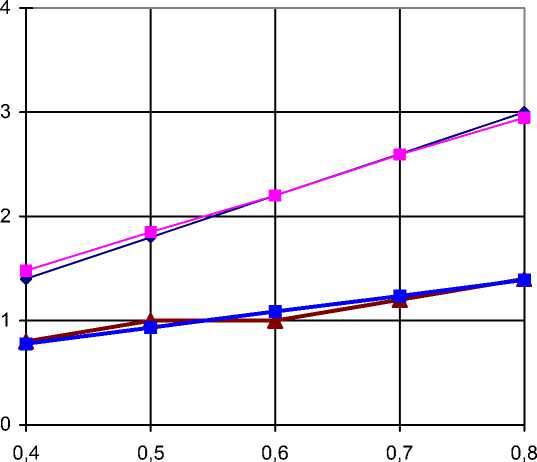
Теоретическая зависимость при верхнем уровне остальных факторов
—*—Экспериментальная зависимость при нижнем уровне остальных факторов
—■—Теоретическая зависимость при нижнем уровне остальных факторов s, м/с
Рис.3. Зависимость потребляемой мощности на резание кукурузы от подачи режущего аппарата
Экспериментальная зависимость при верхнем уровне остальных факторов
Nрез, кВт
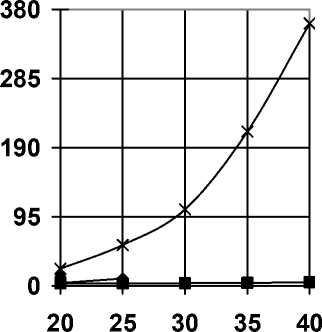
d, мм
Экспериментальная зависимость при верхнем уровне остальных факторов
Теоретическая зависимость при верхнем уровне остальных факторов
Экспериментальная зависимость при нижнем уровне остальных факторов
Теоретическая зависимость при нижнем уровне остальных факторов
Рис. 4. Зависимость потребляемой мощности на резание кустарниковой поросли клёна от диаметра стебля
Мощность, затрачиваемая на измельчение резанием клёна, главным образом зависит от диаметра стеблей (рис.4). Опыты показали, что измельчение при данной зависимости N pe3 = f ( d) на верхних уровнях остальных факторов произошло только при диаметрах 20 и 25 мм, а на нижних только при диаметре 20 мм, при больших диаметрах измельчитель не смог перерезать стебли. Выводы. Определены рациональные параметры ротационно-дискового измельчителя толстостебельных культур:
-
• для подсолнечника и кукурузы (минимальная мощность 0,8 кВт): принцип среза подпорный, подача 0,4 м/с, форма лезвия ножа прямая, частота вращения диска 1200 мин–1, отклонение стебля от вертикали 28°;
-
• для клёна (минимальная мощность 1,6 кВт): принцип среза бесподпорный, подача 0,4 м/с, форма лезвия ножа прямая, частота вращения диска 1200 мин–1, отклонение стебля от вертикали 28°, диаметр стебля 20 мм.
С уменьшением подачи, частоты вращения диска, диаметра стеблей и с увеличением отклонения стебля от вертикали расход мощности снижается. Минимальная мощность измельчения получена при прямой форме лезвия ножей, максимальная – при лезвиях с насечкой. Затраты мощности, расходуемые на измельчение рассматриваемых культур, отражаются в следующей последовательности в сторону увеличения: кукуруза, подсолнечник, клён.
Список литературы Влияние основных параметров измельчителя толстостебельных культур на мощность
- Алёшкин В.Р. Механизация животноводства/В.Р. Алёшкин, П.М. Рощин. -М.: Агропромиздат, 1985. -336 с.
- Мельников С.В. Механизация и автоматизация животноводческих ферм/С.В. Мельников. -Л.: Колос, 1978. -560 с.
- Мельников С.В. Планирование эксперимента в исследованиях сельскохозяйственных процессов/С.В. Мельников, В.Р. Алёшкин, П.М. Рощин. -2-е изд., перераб. и доп. -Л.: Колос, 1980. -168 с.
- Иванцов В.И. Методика экспериментальных исследований и испытаний сельхозмашин: учеб. пособие/В.И. Иванцов/РИСХМ. -Ростов н/Д, 1987. -83 с.
- Проценко Г.И. Расчёт измельчающих аппаратов: текст лекций/Г.И. Проценко/РИСХМ. -Ростов н/Д, 1987. -57 с.
- Веденяпин Г.В.Общая методика экспериментального исследования и обработки опытных данных/Г.В. Веденяпин, 1973. -199 с.
- Адлер Ю.П. Планирование эксперимента при поиске оптимальных условий/Ю.П. Адлер, Е.В. Маркова, Ю.В. Грановский. -М.: Наука, 1976.


