Влияние отложений на расход воды в стальном трубопроводе

Снижение пропускной способности водопроводных труб (СПС ВТ) является актуальной проблемой. Часто это связано с примесями. К примесям воды относятся растворенные и взвешенные твердые вещества. Бикарбонат кальция является растворимой солью. Раствор бикарбоната кальция прозрачный, поскольку кальций и бикарбонат присутствуют в виде ионов атомарного размера, которые недостаточно велики, чтобы отражать свет. Некоторые растворимые минералы придают раствору цвет. Растворимые соли железа образуют растворы бледно-желтого или зеленого цвета; некоторые соли меди образуют растворы интенсивного синего цвета. Несмотря на окраску, эти растворы прозрачные. Взвешенные вещества – это вещества, которые не полностью растворяются в воде и присутствуют в виде частиц. Эти частицы обычно придают воде видимую мутность. Растворенные и взвешенные вещества присутствуют в большинстве поверхностных водоемов [1-12].

Материалы, из которых изготовлены водопроводные трубы, могут существенно влиять на качество питьевой воды. Отмечается миграции примесей из современных многослойных водо проводных труб в питьевую воду. В то время как металлические трубы и муфты содержат тяжелые металлы, из новых пластиковых полиэтиленовых труб также могут выщелачиваться различные соединения, которые могут влиять на обонятельные и вкусовые свойства воды и даже быть вредными для потребителей. В испытаниях труб из сшитого полиэтилена были обнаружены несколько летучих органических соединений, таких как метил- и этил-трет-бутиловый эфиры и трет-бутиловый

ЕDN ADAKKM

• ¹ Великанов Николай Леонидович – доктор технических наук, профессор, профессор НОЦ судостроения, морской инфраструктуры и техники, тел. +7 (4012) 56-48-02 ; e-mail: nikolaj.velikanov@klgtu.ru , ORCID: 0000-0001-6833741, Scopus AuthorID: 57103491500 ;

• ² Наумов Владимир Аркадьевич – доктор технических наук, профессор, профессор кафедры техносферной безопасности и природообустройства, тел . +7 (4012) 99-53-37, e-mail: vladimir.naumov@klgtu.ru , ORCID: 00000003-0560-5933, Scopus AuthorID: 16441812200.

спирт, которые содержались в воде. Было обнаружено, что вода, выдержанная в трубах, выщелачивает антиандрогенные и антиретиноидные Х-по-добные соединения. На содержание металлов в воде влияли не трубы из полиэтилена, а муфты и другие сетевые материалы. Риск выщелачивания соединений был низким и в основном влиял на вкус и запах воды [3-12].

Материалы и методы

В [2] приведена формула для расчета показателя СПС ВТ:

q = ( Q 0 – Q t )/ Q 0 ,             (1)

где   Q0, Qt – расходы воды в новом и после t лет эксплуатации трубопроводе.

Увеличение абсолютной шероховатости

Δ t = Δ0 + α· t ,                (2)

где Δ 0 , Δ t - шероховатость для новых труб и после t лет эксплуатации; α – коэффициент зависящий от группы вод.

Исследование механизма образования отложений в водопроводных трубах проведено в работах [5, 6].

Со временем происходит увеличение толщины стенки S ф [7 – 11] (Рисунок 1).

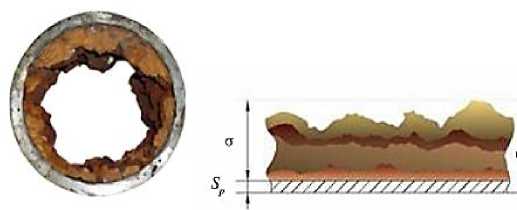
Рисунок 1 – Стенки водопроводных труб [9]

Диаметр проходного сечения трубы dф рассчитывается по формуле dф = D – 2 Sp – 2 σ,          (3)

где D – наружный диаметр трубы;

S p – толщина стенки трубы;

σ – толщина слоя внутренних отложений.

Был уточнен числовой коэффициент в известной формуле гидравлического уклона i g Ф.А. Шевелева для стальных и чугунных труб. При достаточно большой фактической скорости течения ( V ф ≥1,2 м/с) формула имеет вид [9, c. 117]:

i gф = 0,007·( V ф )²/( d ф )^1,3.             (4)

В [12] было предложено аппроксимировать границы между показателем СПС ВТ (1) для разных групп вод из [2] такой функцией:

q^   f_t (t ) = в i ■ t m ,                (5)

где β i , m i – эмпирические коэффициенты, которые были определены методом наименьших квадратов по экспериментальным данным [2];

i = 1, 2, 3, 4, 5 – номер границы: 1 – верхняя граница показателя СПС ВТ группы вод I, 2 – группы вод II, 3 – группы вод III, 4 – группы вод IV, 5 – группы вод V.

В табл. 1 представлены индекс детерминации R ² и значения m, β.

Таблица 1 – Значения эмпирических коэффициентов в формуле (5)

Группа вод	Верхняя граница СПС ВТ	m	β	R 2
I	1	0,595	0,0164	0,97
II	2	0,575	0,0332	0,97
III	3	0,476	0,0699	0,98
IV	4	0,383	0,1221	0,97
V	5	0,270	0,2183	0,98

Во многих системах водоснабжения необходимо поддерживать неизменный расход воды длительное время. Как следует из вышеизложенного, при подаче вод со значительным коррозионным воздействием с течением времени проходное течение трубопровода уменьшается, а гидравлическое сопротивление увеличивается. Если не принимать специальных мер, то расход воды будет уменьшаться. Все меры можно разбить на две группы: 1) снижение гидравлического сопротивления трубопровода, 2) увеличение напора насоса. К первой группе относится очистка трубопровода от плотного осадка, которая в данной статье не рассматривается, и уменьшение гидравлического сопротивления местных сопротивлений (регулирующий вентиль). Ко второй группе – увеличение напора насоса с помощью повышения частоты вращения рабочего колеса (ЧВРК) или замена насоса.

Цель статьи – разработка метода расчета параметров насосной установки, позволяющей поддерживать необходимый расход воды в стальном трубопроводе при уменьшении проходного сечения из-за осаждения примесей.

Воспользуемся формулой, полученной в [12] для оценки уменьшения фактического внутреннего диаметра трубопровода со временем на i-той границе групп вод:

( _. '0 , 377

1 - в i ■ t m i ) . (6) На рисунке 2 показаны результаты расчета по формуле (6).

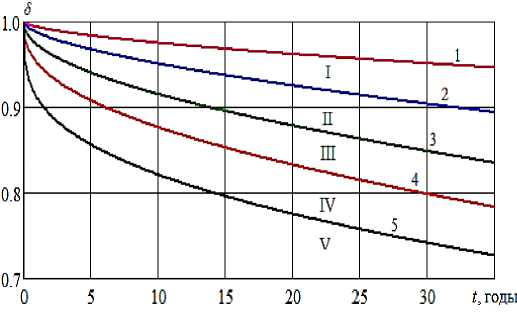
Рисунок 2 - Уменьшение внутреннего диаметра стального трубопровода со временем ( Границы групп вод обозначены арабскими цифрами, сами группы - римскими)

Для расчета потребуются аналитические зависимости напора и затраченной мощности центробежного насоса от подачи. Как в [13], используем многочлены второго порядка:

H = а о + a i Q + a 2 Q ²,        (7)

N = b 0 + b 1 Q + b 2 Q ²,         (8)

где    a0, a 1, a2, b0, b 1, b2 - эмпирические кон станты, найденные методом наименьших квадратов по экспериментальным данным [14].

При условии, что подача насоса задается в м³/с, для ЦНС-60-66 были получены такие значения: a о =81,3 м; a 1 =367,18 с/м²; a 2 = -7,524^10 4 с²/м⁵; b 0 = 8,128 кВт; b 1 = 939,96 кВт/(м³/с); b 2 = -1,814^10 4 кВт/(м³/с)². По рисунку 3 видно, что результаты расчета по формулам (7), (8) хорошо согласуются с экспериментальными данными.

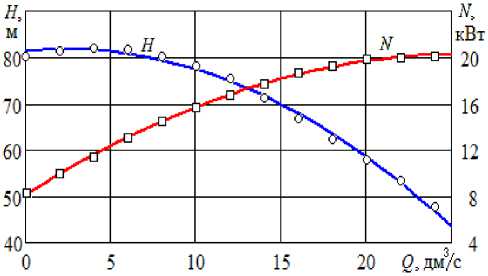
Рисунок 3 - Зависимость напора и затраченной мощности центробежного насоса ЦНС-60-66 от подачи . (Точки - экспериментальные данные [14], линии - расчет по формулам (7), (8))

Переход на другую ЧВРК приводит к изменению рабочих характеристик ЦН. Пересчёт характеристик насоса с номинального значения ЧВРК п_п на некоторое n выполняют, как правило, по известным формулам приведения:

Q/Q n = k , H/H n = k ², N/N_n = k ³, k = n/n_n ,   (9)

где k - относительная ЧВРК, индексом « n » помечены параметры ЦН в номинальном режиме. Известно (см., например, [15]), что первые два равенства (9) выполняются с высокой точностью, а последнее - с погрешностью 3 - 5%. Последнее не будем учитывать в данной статье. Рабочие характеристики ЦК могут быть пересчитаны с учетом изменения ЧВРК [16]:

H = f ( Q , k ) = ( a 0 + a 1 Q/k + a 2 Q ²/ k ²) k 2 ;  (10)

N = ф( Q , k ) = ( b 0 + b 1 Q/k + b 2 Q ²/ k² )• k ³.  (11)

У ЦНС-60-66 номинальная ЧВРК n n =2950 об/мин. На рисунке 4 представлены результаты расчета по формулам (10), (11) для этого насоса.

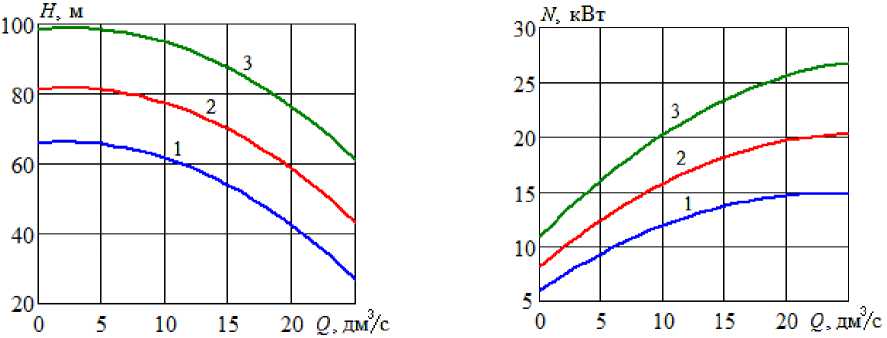
Рисунок 4 - Рабочие характеристики ЦНС-60-66 при различных значениях ЧВРК :

1 - k = 0,9; 2 - k = 1,0; 3 - k = 1,1; a - напор, b - затраченная мощность

По характеристикам насоса (10), (11) могут быть рассчитаны показатели энергетической эффективности: гидравлический коэффициент полезного действия (КПД) η и показатель удельных энергетических затрат (ПУЭЗ) E

П = 100^ g'Q'H/N , E = H/Q,     (12)

где р - плотность воды, кг/м3;

g – ускорение свободного падения, м/с².

Характеристика трубопровода рассчитывается по формуле:

H T ≡ F ( Q ,ζ, d ) = H C + (1,1·λ· L/d + ζ)·8 Q ²/( g π² d ⁴), W= 4 Q/ (π d ²),           (13)

где   HC – статический напор с учетом необхо димого свободного напора, м;

• d – внутренний диаметр трубопровода, м;

L – длина трубопровода, м;

W – средняя по сечению трубы скорость воды, м/с;

• ζ – коэффициент сопротивления регулирующего вентиля;

• 1,1    – коэффициент, учитывающий гидравлическое сопротивление остальных местных сопротивлений;

λ – коэффициент гидравлических потерь по длине трубопровода, в широком диапазоне чисел Рейнольдса может быть рассчитан по формуле Альтшуля:

λ = (Δ /d + 68/Re)^0,25, Re = W·d/ν = 4 Q/ (π d· ν ),

(14) где Δ – абсолютная шероховатость стенок трубы, м; Re – число Рейнольдса;

ν – кинематическая вязкость воды, м²/с.

Вначале рассмотрим регулирование работы насосной установки с помощью дросселирования. Введем следующие обозначения:

T – количество лет, на которые рассчитывается работа насосной установки;

• d 0 , d T – начальное и конечное значение внутреннего диаметра трубопровода, соответственно;

• ζ 0 , ζ T – начальное и конечное значение коэффициента гидравлического сопротивления регулировочного вентиля, соответственно. Д

  

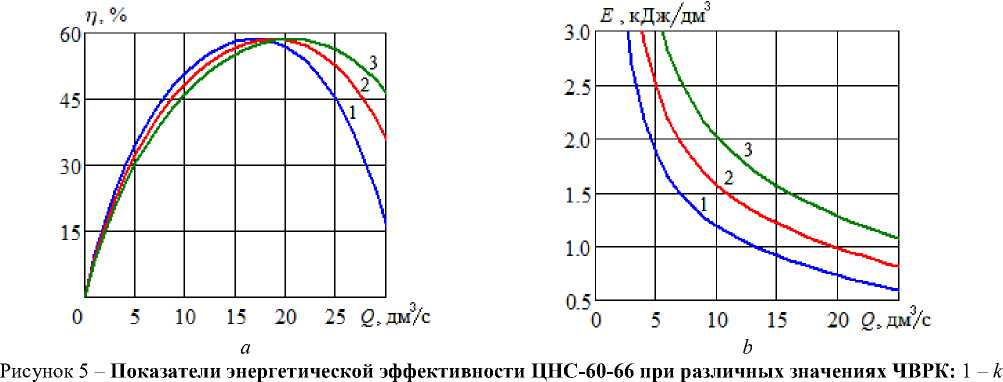
  = 0,9; 2 – k = 1,0; 3 – k = 1,1; a – КПД, b – ПУЭЗ

  
  

По рисунку 5 a при увеличении ЧВРК максимум КПД, не изменяясь, смещается вправо. В действительности, рост ЧВРК приводит к некоторому увеличению максимума КПД. Но это увеличение весьма незначительное. Так в опытах [15]

ля минимизации гидравлических потерь принимаем величину ζ T равной соответствующему значению при полностью открытом вентиле. Задача заключается в определении такого значения ζ 0 , при котором расход останется неизменным, равным заданному значению Q T = Q 0 . Искомое значение коэффициента сопротивления найдем из уравнения:

F ( Q 0 , ζ 0 , d 0 ) = F ( Q 0 , ζ T , d T ). (15)

Считаем, что при регулировании работы насосной установки с помощью изменения ЧВРК коэффициент гидравлического сопротивления вентиля весь период остается равным минимальному значению ζ 0 = ζ T . Величина H T со временем будет расти из-за уменьшения внутреннего диаметра d . Чтобы сохранить неизменной подачу насоса необходимо увеличивать ЧВРК. Для минимизации энергетических затрат принимаем в качестве конечного номинальное значения ЧВРК n T = n n ( k T = 1). Задача заключается в определении такого значения n 0 , при котором расход останется неизменным, равным заданному значению Q T = Q 0 . Искомое значение относительной ЧВРК k 0 найдем из уравнения:

f ( Q 0 , k 0 ) = F ( Q 0 , ζ 0 , d T ). (16) И в (15), и в (16) конечное значение диаметра d T рассчитывается по формуле (6) в зависимости от коррозионных свойств воды.

Результаты расчета и обсуждение

На рисунке 5 представлены результаты расчета показателей энергетической эффективности насоса ЦНС-60-66 по формулам (12) при различных значениях ЧВРК.

при увеличении ЧВРК с 3000 до 10000 об/мин ( k = 3,33) максимум КПД возрос всего на 4%. Здесь же рассматривается случай небольшого изменения ЧВРК ( k = 0,9-1,1). Поэтому увеличением максимума КПД можно пренебречь. По рис. 5 b

ПУЭЗ заметно возрастает с увеличением ЧВРК, что говорит о снижении энергетической эффективности насоса.

В качестве примера рассмотрим систему водоснабжения с многосекционным центробежным насосом ЦНС-60-66 и трубопроводом длиной L = 800 м; d0 = 0,15 м; HC = 55 м; Δ=0,1 мм с периодом жизни T = 20 лет. Необходимо поддерживать постоянный расход воды Q0 = 16,1 л/с (0,0161 м3/с). Перекачиваются воды с содержанием сульфатов и хлоридов больше 500–700 г/м3; их показатели соответствуют верхней границе IV группы вод, строка 4 в табл. 1. По формуле (6) значение внутреннего диаметра трубопровода через 20 лет d20 = d0 (1 – 0,1221·200,387)0,377 = 0,125 м.

Пусть коэффициент гидравлического сопротивления полностью открытого вентиля равен единице. При дроссельном регулировании это будет конечное значение ζ T =1. Тогда решение уравнения (15) дает начальное значение этого коэффициента ζ 0 = 180.

На рисунке 6 представлена графическая интерпретация поддержания постоянного расхода с помощью дросселирования.

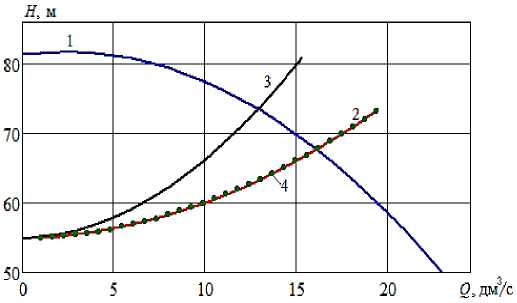
Рисунок 6 - Графическая интерпретация поддержания постоянного расхода с помощью дросселирования: 1 - напорная характеристика ЦНС-60-66 при номинальной ЧВРК;

2 – характеристика трубопровода в начальный момент ζ=180; 3 – характеристика трубопровода в конечный момент при неизменном ζ=180; 4 – характеристика трубопровода в конечный момент при ζ=1

В начальный момент времени вентиль прикрыт так, чтобы ζ0 = 180; линия 2 – это характеристика трубопровода в это время. Пересечение линий 1 и 2 дает рабочую точку насосной установки в начальный момент времени: Q0 =16,1 л/с; H0 =67,8 м. Если оставить неизменном ζ=180, то линия 3 будет характеристикой трубопровода в конечный момент. Тогда в рабочей точке (пересечение линий 1 и 3) Q = 16,1 л/с; H = 73,5 м. Но при дроссельном регулировании вентиль в конечный момент полностью открыт ζT = 1; характеристика трубопровода в это время (линия 3), практически, совпадает с линией 2.

Если проводить регулирование достаточно часто, постепенно снижая величину ζ, то весь период рабочая точка будет неизменной, сохранятся начальные значения Q 0 , H 0 . Значит, останется неизменной начальная затрачиваемая мощность, по формуле (8) N 0 = 18,56 кВт; показатели энергоэффективности по формуле (12): η=57,6%; E = 1,153 кДж/дм³.

При частотном регулировании ζ 0 = 1 и не изменяется. По уравнению (16) найдем значение начальной ЧВРК, чтобы Q 0 =16,1 л/с: k 0 = 0,953 ( n 0 = 2811 об/мин). На рисунке 7 представлена графическая интерпретация поддержания постоянного расхода с помощью частотного регулирования.

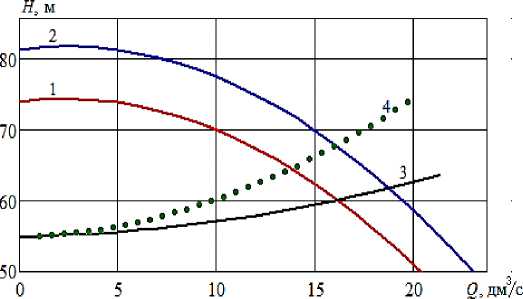
Рисунок 7 - Графическая интерпретация поддержания постоянного расхода с помощью частотного регулирования : 1 – напорная характеристика ЦНС-60-66 при k 0 = 0,953;

2 – напорная характеристика ЦНС-60-66 при k T = 1,0;

3 – характеристика трубопровода в начальный момент ( d 0 = 150 мм); 4 – характеристика трубопровода в конечный момент ( d T = 125 мм)

В отличие от дроссельного регулирования при частотном регулировании со временем напор растет. Поэтому будет расти и затраченная мощность. На рисунке 8 показано, как необходимо увеличивать ЧВРК насоса, чтобы подача оставалась равной Q 0 =16,1 л/с. Значения k найдены по уравнению (16), в котором k считалась неизвестной величиной, а d = δ 4 ( t )· d 0 .

По рисунку 8, вначале затраченная мощность насоса возрастает довольно быстро, а затем ее рост становится близок к линейной зависимости. Среднее значение за 20 лет составило 17,71 кВт. Энергетические затраты при дроссельном регулировании получились примерно на 5% больше, чем при частотном регулировании.

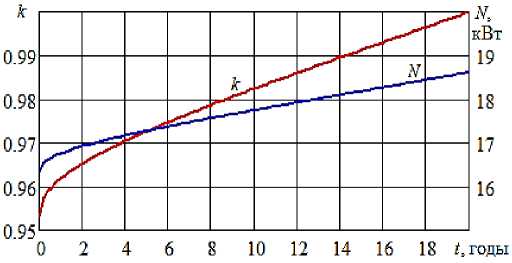
Рисунок 8 – Динамика изменения относительной ЧВРК и затраченной мощности ЦНС-60-66 при частотном регулировании

Заключение

Таким образом, предложены формулы расчета параметров двух способов поддержания необходимого расхода воды в стальном трубопроводе при уменьшении проходного сечения из-за осаждения примесей. Энергетические затраты центробежного насоса при дроссельном регулировании получились примерно на 5% больше, чем при частотном регулировании. Однако при выборе варианта необходимо учитывать стоимость оборудования для частотного регулирования работы центробежного насоса.