Влияние параллельных вычислений и структуры алгоритмов решаемых задач на оперативность обработки информации в многопроцессорных вычислительных системах

Вводные замечания

Общеизвестно, что решение специальных задач, в частности задач космической деятельности, основывается на законах баллистики, механики и теории полета, а также не-

Анализ данных и интеллектуальные системы разрывно связано с обработкой больших объемов информации за расчетное время как на этапах создания и запуска космических аппаратов (КА), так и в ходе сеансов управления ими [8]. В связи с этим возникает необходимость сокращения времени, затрачиваемого многопроцессорными вычислительными системами (МВС) на обработку данных, необходимых для развертывания и поддержания в работоспособном состоянии конкретной орбитальной группировки. Иными словами, речь идет об увеличении скорости выполнения математических вычислений и, как следствие, повышении оперативности обработки информации в многопроцессорных системах.

Следует отметить, что переход к многопроцессорным системам требует одновременного перехода к параллельным вычислениям, поскольку задействовать вычислительный потенциал многоядерных процессоров можно только в том случае, если разделить выполняемые вычисления на информационно независимые блоки и организовать их выполнение на разных процессорах [4]. Подобный подход позволяет выполнять необходимые вычисления с меньшими затратами времени и тем самым получать максимальное ускорение процесса, которое ограничивается только числом имеющихся процессоров и количеством «независимых» блоков в выполняемых вычислениях [2].

Однако необходимость организации параллельных вычислений приводит к усложнению процесса эффективного применения многопроцессорных компьютерных систем. Это обстоятельство связано с тем, что для использования параллельных вычислений требуется в рассматриваемых алгоритмах (задачах) не только определять саму возможность распараллеливания, выделять независимые блоки и организовывать их выполнение, но и оценивать получаемый выигрыш во времени, если таковой имеется, по сравнению с последовательным решением поставленной задачи [4].

Общий подход к распараллеливанию алгоритмов решаемых задач

Одна из основных проблем параллельного программирования – выявление возможности распараллеливания существующих последовательных алгоритмов решаемых задач, а также непосредственно сам процесс распараллеливания алгоритмов, связанный с их дальнейшей программной реализацией.

Решение этой проблемы целесообразно проводить в несколько этапов.

• 1.    Поскольку целью распараллеливания является повышение оперативности решения различных прикладных математических задач, то основополагающим является обобщение этих задач и отнесение их к соответствующим разделам математики для дальнейшего детального рассмотрения по этим разделам.

• 2.    Последующий анализ задач, решаемых в рамках конкретного раздела математики, связанный с определением возможности их распараллеливания и формирования единой параллельно-последовательной задачи. Это позволяет увеличить оперативность решения всех рассматриваемых задач раздела.

• 3.    Аналогичное рассмотрение остальных исходных последовательных алгоритмов решения задач по каждому из рассматриваемых разделов математики и составление их параллельно-последовательных алгоритмов для решения поставленных задач.

• 4.    В заключение процесса преобразования алгоритмов происходит их программная реализация и оценка эффективности процедуры распараллеливания.

Влияние параллельных вычислений и структуры алгоритмов решаемых задач...

Анализ алгоритмов указанных выше задач показывает, что их условно можно разделить на три группы:

• 1)    полностью последовательные алгоритмы – самостоятельные, независимые алгоритмы, которые невозможно распараллелить, но можно реализовывать программно на любом из процессоров многопроцессорной вычислительной системы (ВС) в первоначальном виде [3];

• 2)    смешанная группа алгоритмов , структура которых может быть представлена в виде параллельно-последовательного графа (ПП-графа) и частично реализуется средствами параллельного программирования на многопроцессорных ВС [6];

• 3)    полностью параллельные алгоритмы – группа алгоритмов, представляющих собой параллельную структуру, состоящую из независимых ветвей (потоков), одновременная программная реализация которых на многопроцессорных ВС вообще не вызывает затруднений [3].

Содержательная постановка задачи

На содержательном уровне постановку задачи можно сформулировать следующим образом.

• 1.    Имеется ограниченный набор разнотипных по структуре алгоритмов решения специальных задач.

• 2.    Требуется провести анализ структур алгоритмов, выявить необходимость и возможность их распараллеливания.

Не вдаваясь в подробности и тонкости работы с различными группами алгоритмов, для обобщения их анализа остановимся на самой большой и сложной группе – смешанной, позволяющей достаточно наглядно продемонстрировать весь процесс параллельно-последовательной обработки данной группы алгоритмов.

Как уже отмечалось, решение специальных задач обычно связано с обработкой больших объемов информации на различных этапах существования сложных технических систем – при их проектировании, создании и эксплуатации. Это в полной мере относится к техническим системам космического назначения. Создание указанных систем неразрывно связано с разработкой алгоритмов их функционирования и определением путей возможного распараллеливания вычислений, что, в свою очередь, влечет за собой увеличение скорости выполнения математических вычислений и, как следствие, повышение оперативности обработки информации в многопроцессорных ВС.

Рассмотрим в качестве примера анализа одного из указанных выше типов алгоритмов решение задачи дистанционного зондирования Земли из космоса (ДЗЗ) [8]. При этом съемка и сжатие изображений на борту космического аппарата (КА) должны осуществляться с автоматизированным выбором коэффициента сжатия изображений, что будет уменьшать временные затраты на сжатие графических изображений на борту и при передаче их на Землю [8]. При этом задача повышения качества сжатия графических изображений решается за счет выбора наиболее подходящего метода сжатия, а повышение скорости передачи графических изображений на Землю – за счет организации параллельной обработки информации на борту КА. Совместное решение этих двух задач в целом существенно влияет на повышение оперативности обработки информации в бортовых вычислительных системах (БВС) [5].

Анализ данных и интеллектуальные системы

Анализ [1, 7] показал, что среди методов сжатия изображений целесообразно выбрать наиболее подходящий метод по качеству сжатия. Сжатие данных без потерь позволяет восстанавливать исходные несжатые данные с точностью до бита. Эта характеристика, как правило, необходима для текстовых файлов, баз данных, двоичных объектных файлов.

Цель любого алгоритма сжатия с потерями – достижение высоких коэффициентов сжатия за счет потери некоторых битов таким образом, чтобы восстановленные данные были достаточно близки к оригиналу.

Широко распространенным алгоритмом сжатия информации с потерями является алгоритм, основанный на методе дискретного косинусного преобразования (ДКП), двумерный вариант которого применяется для матриц элементов изображения размерностью 8 × 8 пикселов [7].

Дискретное косинусное преобразование физически представляет собой преобразование массива пикселов изображения в массив значений пространственной частоты. Это преобразование обратимо с точностью до ошибок округления. Такой алгоритм сжатия изображений с потерями позволяет обеспечить существенно более высокую степень сжатия по сравнению с алгоритмами сжатия без потерь. Суть метода заключается в том, что при преобразовании выполняется вычисление косинусных коэффициентов [7].

Так, например, массив из N пикселов может быть представлен в виде взвешенной суммы N косинусных функций с различными частотами, а матрица из N х N пикселов - взвешенной суммой N х N косинусных функций [9].

Реализация предложенной схемы проверки выбранного алгоритма из группы смешанных алгоритмов для упомянутой задачи дистанционного зондирования Земли опирается на методику параллельного программирования, которая объединяет в себе перечисленные ниже аппаратно-программные компоненты [4]:

• •    многоядерные процессоры или микропроцессоры (например, четырехъядерные компьютеры с процессором Intel Core 2 Quad Q8300 2,5 GGz);

• •    операционные системы (например, Windows, Linux, бортовые ОС);

• •    программы создания приложений – проектов ОС (например, Visual Studio);

• •    интерфейс параллельной программы (например, Open MP).

Технология проведения исследований параллельно-последовательного алгоритма сводится к составлению параллельной программы и серии нескольких вариантов компьютерных прогонов с помощью программного диспетчера задач, меняющего для каждого прогона число процессорных ядер компьютера и число обрабатываемых блоков данных.

В ходе реализации прогонов выполняются следующие действия.

Прогон № 1

Группа заданных снимков дистанционного зондирования Земли в виде последовательных блоков размером 8 × 8 пикселов обрабатывается программно на одном из ядер многоядерного компьютера. Такой размер блока выбирается вследствие двух причин [8]. Во-первых, сложность вычислений быстро растет с увеличением размера обрабатываемого блока, поэтому блоки больших размеров оказывают чрезмерную нагрузку на вычислительные ресурсы. Во-вторых, исследования различных изображений показали, что ограничение обрабатываемой области этими размерами не приводит к потерям.

Влияние параллельных вычислений и структуры алгоритмов решаемых задач...

В результате обработки программы происходит сжатие данных, а на ее входе и выходе с помощью процедуры omp_get_wtime (void) средств интерфейса Open MP фиксируется время выполнения.

Прогон № 2

Осуществляется распараллеливание группы указанных блоков на два потока, диспетчер задач программно распределяет потоки для выполнения их на двух любых свободных ядрах. Программа выполняется, происходит сжатие данных, снова фиксируется время выполнения программы.

Прогон № 3

Вся группа из четырех блоков данных распараллеливается на четыре потока по одному блоку и направляется для реализации на четыре свободных ядра компьютера. Программа выполняется, происходит сжатие данных, время выполнения программы фиксируется.

Результаты проведенного исследования всех компьютерных прогонов анализируются, сравниваются, затем делаются практические выводы.

Конкретные числовые данные и математические формулы представлены ниже.

Математическая постановка задачи

Пусть при дистанционном зондировании Земли на борту КА проводится оптико-электронная цифровая съемка земной поверхности. При обработке осуществляется сжатие данных, и на пункт сбора отправляются снимки отдельных участков Земли.

Дано :

• 1)    группа из четырех блоков квадратных массивов данных V [ n , k ], состоящих из 64 пикселов (8 × 8) одноцветного изображения каждый;

• 2)    формула прямого двумерного дискретного косинусного преобразования [7]

У¹У¹          ( 2 n + 1 ) i d

( 2 k + 1 ) i d cos            ,

2 N

i , j = 0 ,... N ,

T [ i, j ]=c (i,j )УУ V [ n,k ]cos——— n=0 k=0            2 N где c(i,j) = —N1 ,i или j = 0; c(i,j) = —N2 ,i, i ≠ 0, j ≠ 0; T[i, j] – массив данных в виде пикселов в сжатом состоянии; i, j, n, k – список целочисленных переменных для организации программной циклической обработки данных по формуле прямого двумерного дискретного косинусного преобразования; N – размер стороны квадратного массива данных в пикселах [8 × 8]; V[n, k] – исходный массив данных, состоящий из 64 пикселов [8 × 8];

• 3)    четырехъядерный компьютер;

• 4)    параллельная программа прямого дискретного косинусного преобразования. Требуется:

По алгоритму прямого двумерного дискретного косинусного преобразования программно реализовать прогоны заданных массивов данных на четырехъядерном компьютере.

Провести исследование зависимости повышения оперативности обработки информации от числа ядер компьютера и блоков данных, обрабатываемых параллельно-последовательно.

Организация прогонов программы в ходе исследования при разном соотношении состава блоков данных и количества задействованных процессорных ядер выявила следующие результаты.

Анализ данных и интеллектуальные системы

• 1.    При первом прогоне программы по сжатию изображений на одном процессорном ядре компьютера было последовательно обработано четыре блока данных за 4,8963 мск.

• 2.    При втором прогоне программы по сжатию изображений обработка проведена двумя параллельными потоками по два последовательных блока в каждом на двух процессорных ядрах компьютера за 2,2797 мск.

• 3.    Третий прогон был проведен четырьмя параллельными потоками с участием четырех блоков данных на четырех процессорных ядрах компьютера за 1,2569 мск.

Результаты исследования приведены на рисунке.

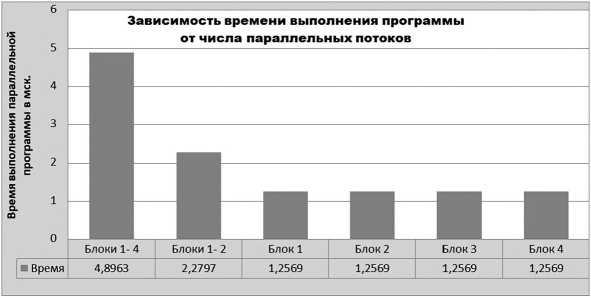
Зависимость времени выполнения программы от числа ее параллельных блоков и количества ядер процессора

Заключение

Итак, параллельные структуры алгоритмов решаемых задач и аппаратных средств вычислительной техники, а также параллельное программирование – это главные составляющие достижения необходимого параллелизма вычислительных процессов и, как следствие, роста производительности работы вычислительных средств и повышения оперативности обработки информации.

Целью проведенного исследования было показать зависимость времени решения задачи от структуры алгоритма и возможности ее распараллеливания с учетом технических возможностей многопроцессорных ВС.

Следует отметить, что алгоритмы задач, отнесенные к группе полностью параллельных алгоритмов, не вызывают затруднений при параллельном программировании, и реализация их на многоядерных вычислительных средствах ограничена только количеством задействованных процессоров (ядер). В этом случае повышение производительности многопроцессорных ВС возможно в основном за счет масштабирования (наращивания числа процессоров или ядер).

Когда имеет место последовательная или параллельно-последовательная обработка данных, повышение производительности многопроцессорных ВС возможно за счет трех составляющих процесса: 1) распараллеливания последовательных или параллельно-последовательных алгоритмов; 2) сжатия данных и 3) масштабирования (наращивания числа процессоров или ядер компьютера).

Влияние параллельных вычислений и структуры алгоритмов решаемых задач...