Влияние параметров лабиринтного уплотнения в турбине низкого давления на кпд ступени

Одной из основных задач при создании газотурбинных двигателей является задача повышения эффективности его узлов, и как следствие, необходимость снижения непроизводительных утечек воздуха, отбираемого в компрессоре на охлаждение турбины, наддува в опорах турбин и компенсации осевых усилий на подшипники. В настоящее время для решения этих задач широко используются лабиринтные уплотнения. Характеристики течений и утечек через лабиринтные уплотнения в турбинах ТРДДФ большой мощности были исследованы Белоусовым А.И. и Наздрачёвым С.В [2]. Определение расхода через лабиринтные уплотнения на этапе проектирования системы охлаждения турбины можно осуществлять путём расчёта математической модели и последующего уточнения с помощью кончено элементного расчёта.

ПОСТАНОВКА ЗАДАЧИ

Для исследования влияния конструкции лабиринтных уплотнений на КПД ступени была построена модель проточной части турбины низкого давления ТРДДФ. Была рассмотрена третья ступень, т.к. турбины низкого давления очень чувствительны к радиальным перетеканиям рабочего тела.

Актуальной проблемой при проектировании турбин, является поиск конструктивных параметров лабиринтного уплотнения, обеспечивающих минимальные утечки газа, что способствует повышению КПД ступени турбины.

Задачей исследования является выявление степени влияния таких конструктивных параметров, как радиальный зазор, количество гребешков лабиринтного уплотнения соплового аппарата, шага между гребешками и угла наклона гребешков на КПД ступени ТНД ТРДДФ.

Была исследована ступень ТНД и рассчитано влияние изменения конструкции указанных элементов на адиабатный КПД ступени (при условии сохранения параметров расходов воздуха и степени расширения).

МЕТОДИКА ИССЛЕДОВАНИЙ

Для решения поставленных задач в программном комплексе AutoGrid 5 построена математическая модель расчётной области ступени турбины, включающая 3D модель ступени,

точниковый член, учитывающий эффекты, связанные с гравитационной силой;

- уравнение состояния газа р = pRT,              (4)

где R – газовая постоянная; T – температура.

При разработке математической модели были приняты следующие допущения. При настройках расчетной модели в программном комплексе Numeca Fine Turbo в качестве рабочего тела использовался идеальный газ со свойствами продуктов сгорания:

Газовая постоянная R составляла 287,3 Дж/ (кг·К).

В качестве граничных условий для серии расчетов были заданы:

Постоянная температура по высоте проточной части на входе в ступень;

Постоянная частота вращения, равная 9225 об/мин;

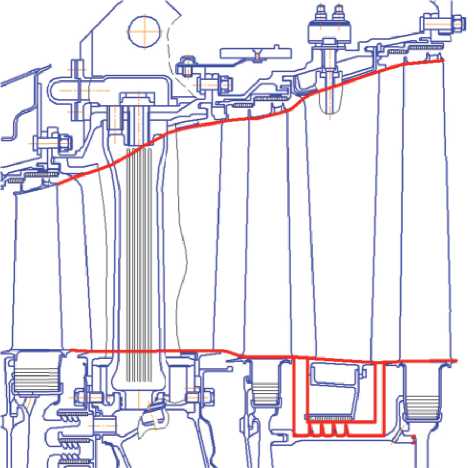
Рис. 1 . Проточная часть исследуемого венца       С_{тепени понижения давления газа в т}урб_ине

а)                                                           б)

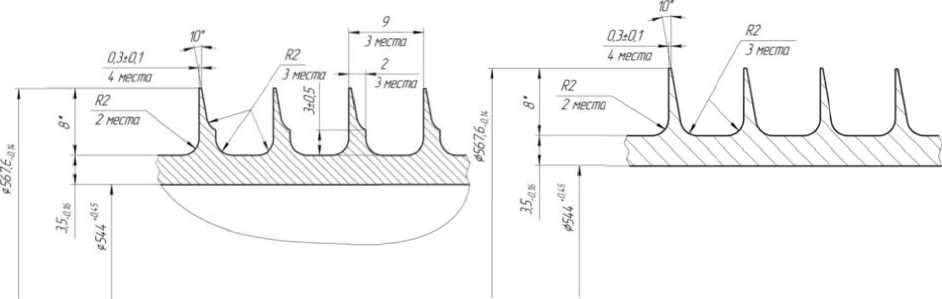
Рис. 2. Параметры зуба а) чертёж б) упрощенная модель а также модель лабиринтного уплотнения выбранного участка турбины.

Построение сеток конечных элементов в доменах ЛВ выполнялось с использованием функции Start Row Wizard.

Математическая модель газодинамического процесса для расчёта ЛУ:

• -    уравнение сохранения полной энергии

^^•(pUHf')^ (1)

• -    уравнение количества движения

d(pU)

^т² + V • [ pU ■ U ) = Vp + V • т ; (2)

• -    уравнение непрерывности

'2v-pu: 0

где ρ – плотность; h_tot – полная энтальпия.

u5

htot-hstat+—; t- время; p - давление; U - вектор скорости; τ – тензор вязких напряжений; SE – ис- в диапазоне 1,4 - 3,2.

Зависимость теплоемкости от температуры определялась по выражению [5]:

Ср = 289,2 + 0,5068 • -0.0001925 • Г² +

+0,2736 • 10⁷ • Г³ , Дж/(кг-К)            ⁽⁵⁾

Вязкость рабочего тела описывалась уравнением Сазерленда:

273 + 200 Т 1,5

^ = 1Д9 •10   • 1Б0+Т • (273) кг/(№с)' (6)

Выбор расчетной сетки для исследования рабочего процесса был выполнен на основе расчета при различных степенях расширения π _T* nTвх*=158,2 с использованием трех расчетных моделей.

Процесс исследования включал в себя определение влияния на КПД ступени изменения следующих конструктивных параметров лабиринтного уплотнения при сохранении степени расширения и расхода воздуха:

• -    радиального зазора между гребешками и сотоблоками;

  
  
  
  

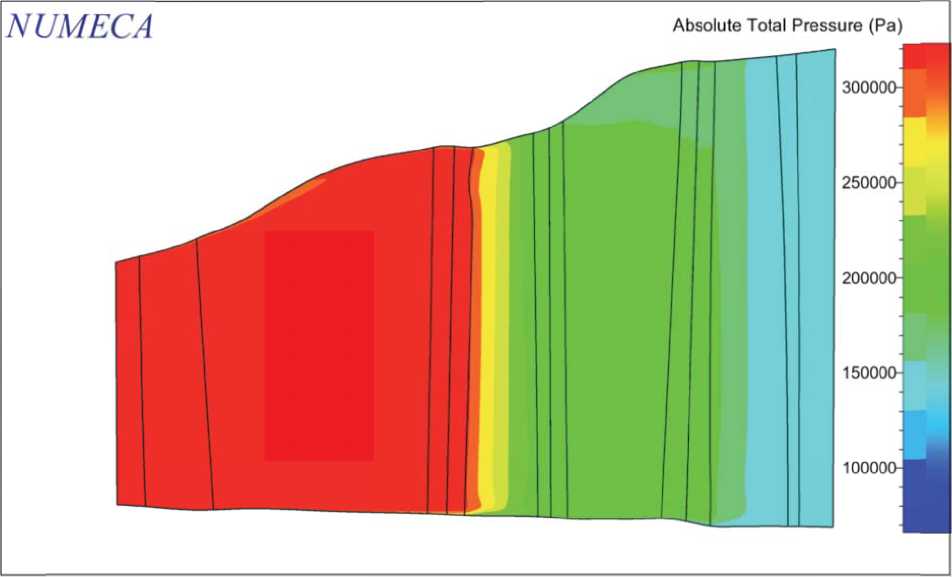
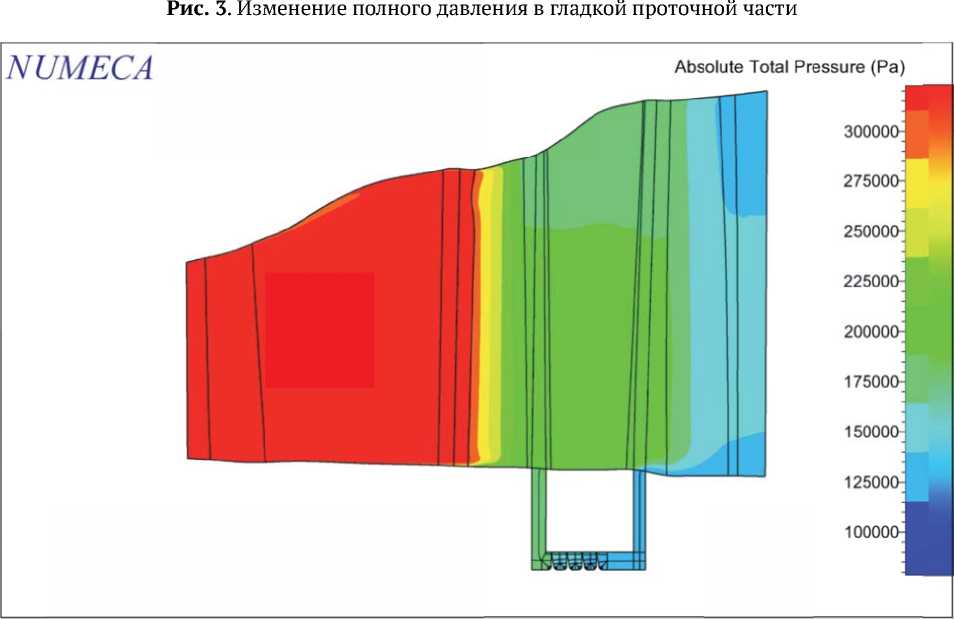
  Рис. 4 . Изменение полного давления в проточной части с лабиринтным уплотнением

  
  

• -    количества гребешков;

• -    шага между гребешками;

• -    угла наклона гребешков;

В качестве первого рассматриваемого критерия влияния конструкции на КПД ступени было рассмотрено 6 вариантов лабиринтного уплотнения с различной величиной радиального зазора (рис 6.) и произведен их расчет, дан- ные которого представлены в табл. 1.

Далее было рассмотрено влияние на КПД ступени количества гребешков уплотнения. Было исследовано 6 вариантов конструкции (рис. 7) и рассчитаны их параметры (табл. 2).

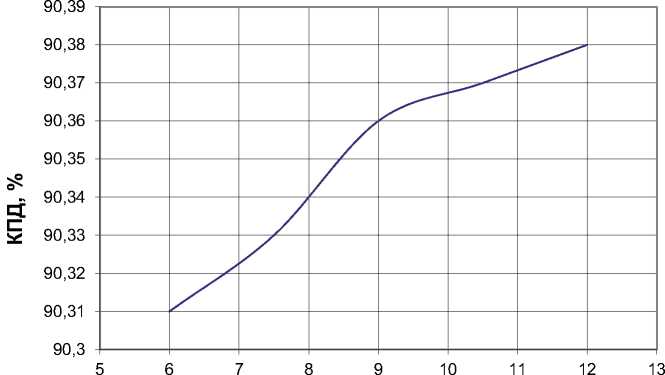
Для выявления влияния шага гребешков на КПД, были созданы 5 моделей (рис. 8), результаты расчета которых представлены в табл. 3.

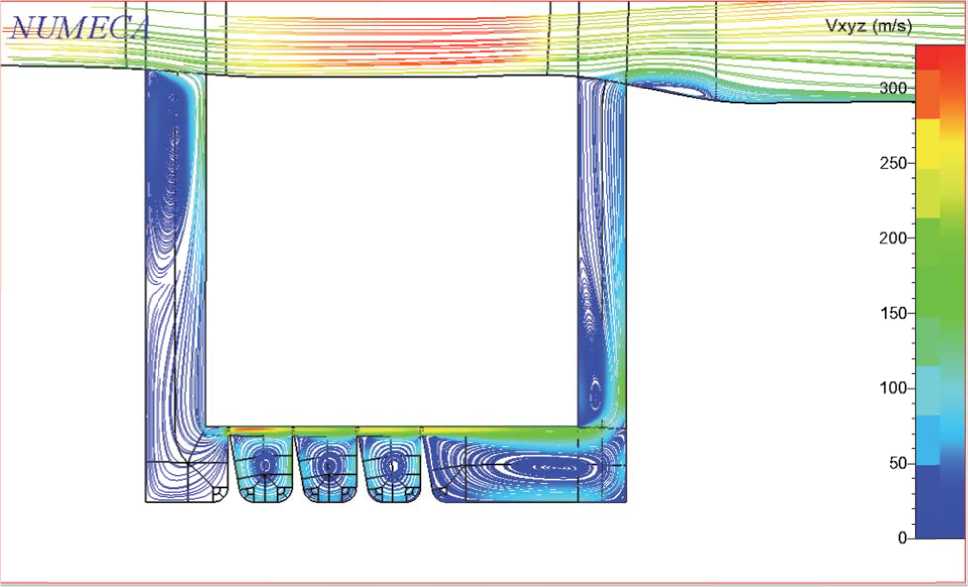
Рис. 5 . Завихрения в лабиринтном уплотнение

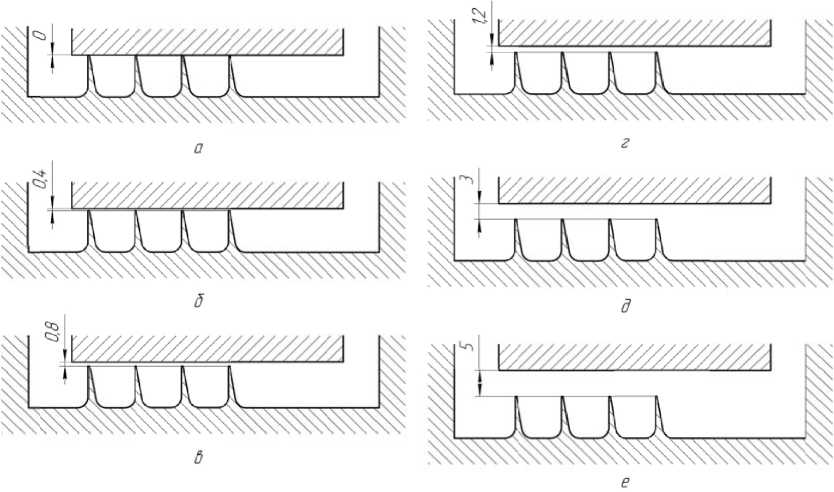
Рис. 6 . Варианты конструкций с различным радиальным зазором

Таблица 1. Изменения параметров ступени в зависимости от радиального зазора в лабиринтном уплотнении

№ модели	зазор, мм	N, об/мин	G b , кг/с	л*	кпд, %
а	0	4703	62,85	2,3	90,52
б	0,4	4703	63,01	2,3	90,49
в	0,8	4703	63,02	2,3	90,45
г	1,2	4703	63,04	2,3	90,36
д	3	4703	63,05	2,3	89,92
е	5	4703	63,07	2,3	89,61

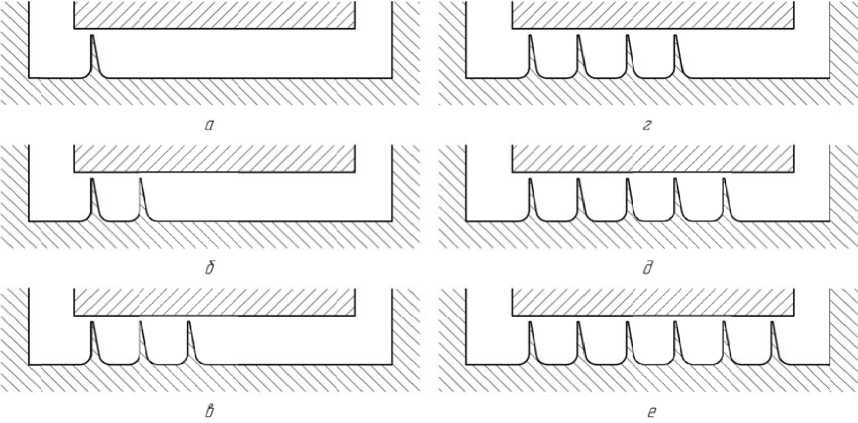
Рис. 7 . Варианты конструкций с различным количеством гребешков

Таблица 2. Изменение параметров ступени в зависимости от количества гребешков в лабиринтном уплотнении

№ модели	Кол-во гребешков	N, об/мин	G b , кг/с	л*	кпд, %
1	–	4703	62,85	2,3	90,52
а	1	4703	63,03	2,3	90,26
б	2	4703	63,03	2,3	90,29
в	3	4703	63,03	2,3	90,33
г	4	4703	63,04	2,3	90,36
д	5	4703	63,03	2,3	90,38
е	6	4703	63,02	2,3	90,39

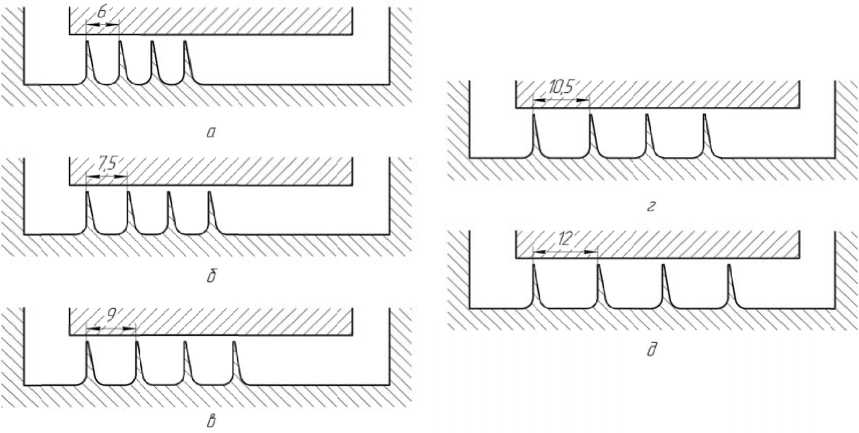
Рис. 8. Варианты конструкций с различным шагом гребешков

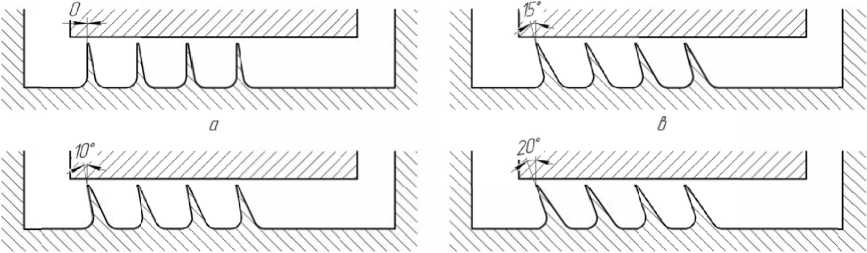
Так же было рассмотрено влияние на КПД ступени угла наклона гребешков, созданы 4 модели (рис. 9). Результаты представлены в табл. 4.

ЗАКЛЮЧЕНИЕ

Используя полученные данные, было вы- явлено влияние следующих параметров лабиринтного уплотнения: радиального зазора, количества гребешков, шага между гребешками и углом наклона гребешков на КПД ступени турбины низкого давления ТРДДФ.

На рис. 10 видно, что изменение отношения величины радиального зазора между гребешка-

Таблица 3. Изменение параметров ступени в зависимости от шага гребешков в лабиринтном уплотнении

№ модели	Шаг между гребешков, мм	N, об/мин	G b , кг/с	л*	кпд, %
1	-	4703	62,85	2,3	90,52
а	6	4703	63,03	2,3	90,31
б	7,5	4703	63,03	2,3	90,33
в	9	4703	63,04	2,3	90,36
г	10,5	4703	63,03	2,3	90,37
д	12	4703	63,02	2,3	90,38

В                                             г

Рис. 9 . Варианты конструкций с различным углом наклона гребешков

Таблица 4. Изменение параметров ступени в зависимости от угла наклона гребешков в лабиринтном уплотнении

№ модели	Угол гребешка, град	N, об/мин	G b , кг/с	л*	кпд, %
1	-	4703	62,85	2,3	90,52
а	0	4703	63,04	2,3	90,36
б	10	4703	63,03	2,3	90,36
в	15	4703	63,02	2,3	90,36
г	20	4703	63,02	2,3	90,36

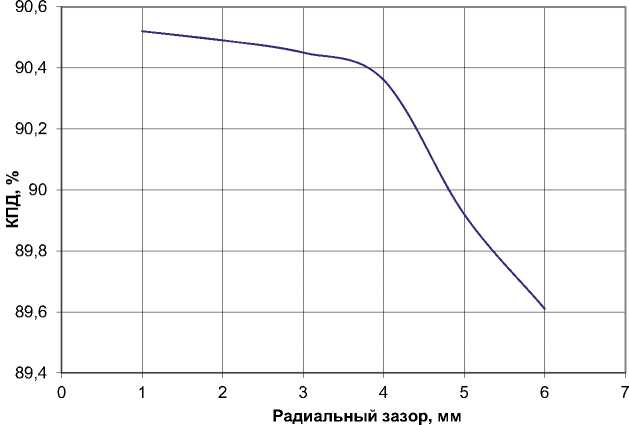
Рис. 10. График зависимости КПД от радиального зазора ми и сотоблоками к диаметральному размеру, на котором расположено лабиринтное уплотнение (относительного зазора) в диапазоне от 0,0018 до 0,0073 оказывает меньшее влияние на КПД ступени, чем дальнейшее его увеличение, которое приводит к значительному снижению КПД, так как вихри, образующиеся в рабочем теле из-за конструкции лабиринтного уплотнения, перестают препятствовать свободному перетеканию воздуха через уплотнение. Рис. 11 иллюстрирует существенное увеличение КПД при увеличении количества гребешков до 5 штук. При дальнейшем увеличении количества гребешков темп роста КПД заметно снижается, что может объясняться достижением преде- ла возможности предотвращения перетекания данной конструкцией. По графику, изображенному на рис. 12, можно сделать вывод о положительном влиянии на КПД ступени увеличения шага между гребешками, однако, дальнейшее увеличение шага (при выбранном их количестве) ограниченно пространством для их размещения в данной конструкции. Из анализа рис. 13 следует, что для данной конструкции лабиринтного уплотнения в системе проточной части ТНД ТРДДФ, угол наклона гребешков не влияет на КПД, т.к. вне зависимости от угла, площадь, занимаемая вихрем не изменяется, происходит его перераспределение, что не существенно влияет на газодинамику притрактовой полости.

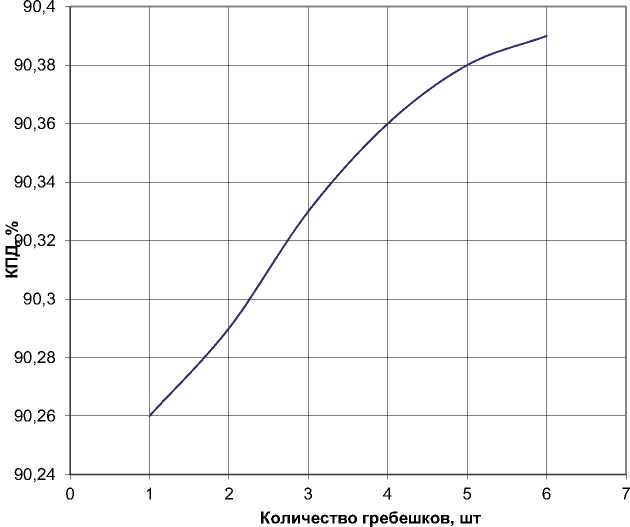
Рис. 11 . График зависимости КПД от количества гребешков

Шаг между гребешками, мм

Рис. 12 . График зависимости КПД от шага между гребешками

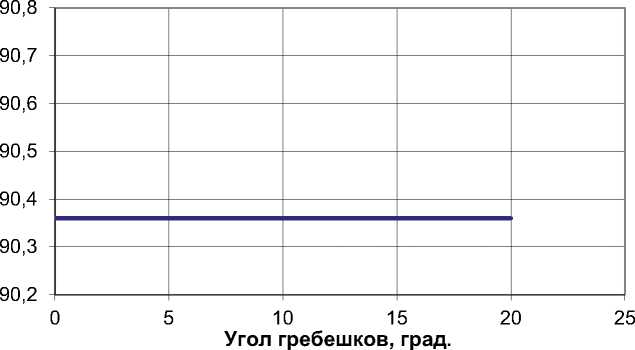
Рис. 13 . График зависимости КПД от угла наклона гребешков

Используя серию CFD-расчетов, было получено решение, позволяющее оценить влияние радиального зазора, количества гребешков, шага между гребешками и угла наклона гребешков на КПД ТНД ТРДДФ, что способствует созданию модели ТНД с уменьшенными утечками.