Влияние параметров рекуперативного объема на динамические характеристики пневмопривода при торможении

УДК 62.593                                               

Введение. Рассмотрены способы энергосбережения в пневматическом приводе. Интерес представляет способ торможения созданием противодавления в выхлопной полости пневмопривода. При этом энергия сжатого воздуха накапливается в рекуперативном объеме. Задавая начальные параметры рекуперативного объема, возможно управлять динамикой торможения. Цель работы — создание математической модели, описывающей динамические процессы, происходящие в пневматическом приводе при торможении противодавлением, с постоянной массой, заключенного в полостях пневмодвигателя воздуха, и с учетом изменения начальных параметров тормозного объема.

Материалы и методы. Предложена математическая модель, описывающая изменение скорости движения выходного звена, давлений и температур в полостях пневмопривода в зависимости от начальных параметров рекуперативного объема. Решение математической модели осуществлялось методом численного интегрирования.

Результаты исследования. Получены зависимости скорости выходного звена, давлений и температур в полостях пневмопривода от начальных параметров рекуперативного объема. Адекватность полученной математической модели подтверждена по критерию Фишера.

Обсуждения и заключения. Полученные результаты могут быть полезны для решения задач энергосбережения в пневмоприводах при организации торможения противодавлением. Применение рекуперативного объема повышает технологическую гибкость привода при его переналадке и расширяет возможности энергосбережения.

Introduction. Methods of energy saving in pneumatic drive are considered. The method of braking by creating back pressure in the exhaust cavity of the pneumatic actuator is of interest. Under braking, the compressed air energy is stored in the recuperative volume. It is possible to control the braking dynamics through setting the initial parameters of the recuperative volume. The work objective is to create a mathematical model describing the dynamic processes taking place in the pneumatic drive under braking by backpressure, with a constant mass enclosed in the cavities of the air motor, and considering variation of the initial parameters of the braking volume.

Materials and Methods. A mathematical model is proposed that describes the speed change of the output link, pressures and temperatures in the cavities of the pneumatic drive depending on the initial parameters of the recuperative volume. The solution to the mathematical model is carried out by the numerical integration method.

Research Results. The dependences of the output link velocity, pressures and temperatures in the pneumatic drive cavities on the initial parameters of the recuperative volume are obtained. Adequacy of the built mathematical model is confirmed by Fisher's criterion.

Discussions and Conclusions. The results obtained can be used to solve the problems of energy saving in pneumatic drives under the organization of backpressure braking. The use of recuperative volume increases the technological flexibility of the drive during its readjustment and extends the possibilities of energy saving.

Машиностроение и машиноведение

Образец для цитирования. Сиротенко, А. Н. Влияние параметров рекуперативного объема на динамические характеристики пневмопривода при торможении / А. Н. Сиротенко, С. А. Парко, Ваел Саллум // Вестник Дон. гос. техн. ун-та. — 2018. — Т. 18, № 4. — С. 379-384.

Введение. Пневматические приводы широко применяются для автоматизации и механизации вспомогательных технологических процессов. Энергопотребление пневмофицированного оборудования может составлять более 20% общего потребления предприятия. Поэтому вопросы энергосбережения в пневмоприводах являются весьма актуальными [1 – 3]. Такие особенности, как сжимаемость рабочей среды и инерционность выходных звеньев, затрудняют безударное торможение , усложняют управление и конструкцию привода [1, 3, 4]. Управлять законом торможения пневмопривода можно как воздействием на регулирующее устройство [1, 2, 5, 6 ], так и выбором рационального способа торможения [ 7 – 9].

Перечисленные особенности пневмопривода позволяют использовать сжатый воздух, как тормозной демпфер и накапливать энергию торможения, что эффективно реализуется при торможении пневмопривода способом противодавления [ 7]. Изменяя координату переключения на торможение, давление в тормозной и нагнетательной полости, подключая к выхлопной полости дополнительный объем, возможно не только обеспечить безударное торможение, но и рекуперировать энергию сжатого при торможении воздуха [2, 7, 10]. Задавая начальные параметры рекуперативного объема, можно влиять на тормозные и энергоскоростные параметры пневмопривода. Однако данный вопрос исследован в настоящее время недостаточно.

Цель исследования — создание математической модели, описывающей динамические процессы , происходящие в пневматическом приводе при торможении противодавлением, с постоянной массой, заключенного в полостях пневмодвигателя воздуха и с учетом изменения начальных параметров тормозного объема .

Постановка задачи. Требуется математически описать зависимость динамических характеристик пневматического привода при торможении противодавлением от начальных параметров рекуперативного объема.

Математические зависимости. Рассмотрим торможение способом противодавления путем полного перекрытия магистралей нагнетания и выхлопа. Недостатком способа является то, что при изменении рабочего перемещения и внешней нагрузки на выходное звено необходимо заново настраивать координату включения торможения . Альтернативой является подключение в момент торможения к тормозной полости пневмодвигателя рекуперативного объема. Задавая его начальные параметры до торможения, возможно влиять на конечное давление в тормозном объеме и тормозной путь выходного звена пневматического привода [8].

Для математического описания газодинамических процессов, протекающих в полостях пневмопривода , были сделаны следующие допущения [10, 12]: давление в магистралях принимаем постоянным; термодинамические процессы, протекающие в полостях пневмопривода , рассматриваем как адиабатные ; рабочую среду в полостях пневмопривода, сжатую при торможении , рассматриваем как идеальный газ .

В основе торможения противодавлением лежит принцип создания силы сопротивления движению выходного звена пневмодвигателя. Это достигается частичным или полным перекрытием каналов нагнетания и выхлопа. Полное перекрытие более эффективно , так как отсутствует сброс сжатого при торможении воздуха из тормозной полости . Динамика пневмопривода до торможения определяется известной системой уравнений, учитывающей подкритический и надкритический режимы истечения [ 10].

Параметры пневмопривода показаны на рис . 1. Параметры рабочей среды обозначены как : V_м, p_м, T_м — объем, давление и температура сжатого в магистрали воздуха соответственно ; V п , p п , T п , — объем, давление, температура воздуха, сжатого в поршневой полости пневмодвигателя; V_ш, p_ш, T_ш — объем , давление, температура воздуха сжатого штоковой или тормозной полости пневмодвигателя; V рек , p рек , T рек — объем , давление, температура сжатого воздуха в рекуперативном объеме ; V a _т, p a _т, T a _т — объем , давление, температура атмосферного воздуха. Геометрические параметры пневмодвигателя имеют следующее обозначение: F п , F ш — поршневая и штоковая рабочие площади пневмодвигателя; f_н, f_в — площади проходных сечений магистралей нагнетания и выхлопа соответственно; х, х 0 _п, х 0 _ш — координаты текущего перемещения, постоянного поршневого и штокового «пассивных» объемов соответственно; s — максимальный рабочий ход; Р — полезная нагрузка .

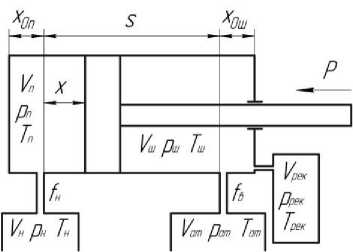
Рис. 1. Параметры пневмопривода при торможении противодавлением в рекуперативный объем

При торможении в полостях пневмодвигателя находится постоянное количество сжатого воздуха. Считаем, что теплообмен с окружающей средой незначителен, поэтому термодинамический процесс считаем адиабатным, с показателем адиабаты k=1,4 [10]. Для торможения золотник распределителя переключится в нейтральное положение и перекроет проходные каналы магистралей нагнетания и выхлопа ( f_н=0, f_в=0) . Время переключения золотника распределителя не учитываем, каналы нагнетания и выхлопа перекрываются одновременно. Соединение рекуперативного объема с штоковой полостью пневмодвигателя считаем мгновенным.

С учетом данных допущений полости , давление рабочей среды в поршневой полости пневмодвигателя представим в следующем виде:

(1.1)

рп=(vпт/vп) ∙ рпт, где рп, рпт — текущее и начальное давление в момент переключения на торможение в поршневой полости пневмодвигателя; vп, vпт — текущий и начальный удельные объемы поршневой полости пневмодвигателя; k — показатель адиабаты.

Сократим уравнение (1.1), разделив его на площадь поршня пневмодвигателя : р_п=((х 0 _п+х_т)/(х 0 _п+х)) ∙р_пт ,

(1.2)

где х 0 п , х т , х — координаты: начальная, включения торможения и текущего положения поршня пневмодвигателя соответственно.

В момент переключения распределителя на торможении рекуперативный и тормозной объемы объединяются, в этом случае параметры сжатого воздуха определятся следующие системой (1.3):

(1.3) < шт p рек

■ vk   = p ■ vk шт    1

■ vk   = p ■ vk рек      2

(1.3.1)

(1.3.2)

где v_шт , v_рек — удельные объемы сжатого в начале торможения в штоковой полости и рекуперативном объеме воздуха ; v 1 , v 2 — «условные» удельные объемы воздуха в штоковой полости и рекуперативном объеме ; р_шт, р_рек, р — давления сжатого вначале торможения воздуха в штоковой полости, рекуперативном объеме и в «объединенном» объеме соответственно.

В системе уравнений (1.3) выразим удельные объемы v 1 , v 2 :

(1.4) ^

k p ■ v шт шт

k

= Р ■ ^v 1 ^

^V ■! p шт к шт

p

k

1         ■ v рек рек

k

k

= p ■ v

^ V ■! p рек к рек

p

■

шт

(

V шт

k

= р ■

k

^V 1

^

m к шт у

= V1 ■ ( ^p )

^ p

k

k

■

рек

m шт у

(1.4.1)

V рек

k

= Р ■

(

V

k

^

m рек >

m рек >

= ^V 2 '⁽ p ) k

Машиностроение и машиноведение

(1.4.2)

где V_шт, V_рек, — штоковый и рекуперативный объемы соответственно на момент начала торможения, ; V 1 , V 2 — штоковый и рекуперативный объемы, соединенные в «объединенный» объем ; m шт , m рек — масса воздуха, сжатого в штоковом и рекуперативном объёме на момент начала торможения ; р — давление в «объединенном» объеме .

Для определения давления в «объединенном» объеме просуммируем уравнения (1 .4 .1) и ( 1.4.2):

p =

V •( p )  + V шт шт     рек

V +v

V 1 ⁺ V 2

k

k

( 1.5)

Используя уравнение Клапейрона , найдем температуру рабочей среды в «объединенном» объеме :

V + V p-v = R . T ^ T = p = P • шт рек R R V V

(1.6)

шт , Рек v + v

( шт рек J где Т — температура сжатого при торможении в «объединенном» объеме воздуха; R — универсальная газовая постоянная,.

Окончательную зависимость температуры воздуха в тормозной полости пневмопривода от начальных параметров рекуперативного объема получим , раскрыв значения удельных объемов в уравнении (1.6) и сократив его на площадь штоковой полости пневмодвигателя:

T = p • ^{(( 5 +} x 0 ш

+ h рек

- x )

^{( 5 +} x 0 ш

T • T шт рек

x) • T рек

• P шт

+ h рек

• T шт

• P

))

(1.7)

рек

где h рек — приведенный к штоковой площади пневмодвигателя, рекуперативный объем ; Т, Т шт , Т рек — абсолютные температуры в «объединенном», штоковом и рекуперативном объемах соответственно .

d2x m^y = Pn ■ Fn ~P-Pш ■ Fш dt2

(1.8.1)

Pn =

k

x 0 n + xm

I ^x 0 n

+ x

^{( 5 + x} 02

■ pnm

(1.8.2)

^{- x} )⁽ Pшm ) ^{k +} hрек

( p рек ) ^k

k

P =

Tn =

f P nm

P n J

(1.8.3)

(1.8)

( ^{5 + x} 02 ⁺ h рек ^x )

k - 1

1 ^k T

• Tnm

T = p • ^{(( 5} + x 0 ш + hрек - x )

T • t ш рек

^{( 5 + x} 0 ш  ^x ) ^Трек • ^pш ⁺ hрек • ^тш • ^Pрек

))

(1.8.4)

(1.8.5)

Движение поршня пневмодвигателя описывается уравнением (1.8.1). Общая система уравнений процесса торможения пневматического устройства будет иметь вид (1.8). Здесь: m — приведенная к штоку пневмодвигателя масса рабочего органа; Тн — абсолютная температура воздуха в магистрали нагнетания; Тпт — начальное значение температуры воздуха в поршневой полости пневмодвигателя в момент переключения на торможения.

Уравнения (1.8.2) и (1.8.3) описывают изменение давления, а уравнения (1.8. 4 ) и ( 1.8.5) — изменение температуры в поршневой и тормозной полостях пневмодвигателя соответственно .

Совместное решение системы уравнений , описывающей динамику торможения пневмопривода (1.8) и его разгон методом численного интегрирования Рунге - Кутта [14] , позволяет изучить зависимость динамических характеристик пневмопривода от начальных параметров рекуперативного объема. Стендовая оценка характеристического совпадения теоретических и практических зависимостей показала удовлетворительную сходимость [ 13] , что позволило провести проверку адекватности полученной математической модели по критерию Фишера. Для этого был проведен двухфакторный эксперимент. Независимыми факторами были выбраны начальное давление и величина рекуперативного объема . Факторы изменялись согласно трем уровням варьирования, что позволило использовать девять комбинаций сочетания факторов при повторении каждого опыта трижды .

Математическая модель адекватна практическим результатам, полученным при экспериментальной проверке , так как расчетное значение критерия Фишера составило 2,67 , что меньше табличного (2,7) [15].

Полученные результаты позволили перейти к вычислительному эксперименту, который позволит определить рациональные комбинаций начальных параметров рекуперативного объема для заданного закона торможения пневмопривода и обеспечения при этом высоких энергоскоростных показателей.

Выводы:

• 1.    Разработана математическая модель , адекватно описывающая динамические процессы , протекающие в полостях пневматического привода при торможении противодавлением с накоплением энергии сжатого воздуха в рекуперативный объем.

• 2.    Получены математические зависимости параметров пневматического привода от начальных параметров рекуперативного объема при торможении противодавлением.