Влияние параметров серводвигателей на динамические свойства системы сверления глубоких отверстий спиральными свёрлами

Работа выполнена в рамках инициативной НИР.

деляется условиями трения во всех элементах привода). В этом случае уравнения, связывающие траектории движения исполнительных элементов с напряжениями якорей двигателей можно представить в виде [2,4,9]:

к^=иДП-с^2-^, где со,, Ij, / = 1,2 — соответственно угловые скорости вращения шпинделя и двигателя, обеспечивающего движение пиноли, а также токи якорей двигателей постоянного тока с якорным управлением (индекс «1» соответствует серводвигателю вращения шпинделя, а «2» — серводвигателю, обеспечивающему управление движением пиноли); U,, /=1,2 — напряжения якорей двигателей, с помощью которых управляется частота вращения шпинделя и серводвигателя подачи; J,, / = 1,2 — моменты инерции роторов двигателя вместе со шпинделем и механической частью привода подачи (определяется конструктивными особенностями силовых сверлильных головок); R,, Ц, / = 1,2 — активные сопротивления и индуктивности якор ных цепей; с^, с^, / = 1,2 — конструктивные параметры двигателей; М, z (t) = М, (t) + MjQ, / = 1,2 — моменты, действующие на роторы двигателей, состоящие из моментов, формируе мых в зоне резания М, (t), и постоянных моментов, не связанных с процессом обработки MjQ

Для дальнейшего рассмотрения систему (1) удобно представить в следующем виде:

^Ш0,1 V ) ^ШМД\¹ ) ¹ ЭМ¹ Э   ^2    ¹ ЭМ       ТШ1^,

О) ft) —О) ft) = T2T2----2     Т 2 ---2 ^+00 ft)

^Ш0,2 V /   W,2 V / ЭМ¹ Э ^2 ЭМ          ^Ш2 V )'

LL(tA где соО/ (Г) =      - ^ ^ / / =1/2 — угловые скорости вращения сервоприводов на холостом ходу (в предположении, что нагрузка на якоря двигателей, обусловленная процессом реза- ния, отсутствует); шм, (f) = —

.(/)    ' V /    3 д м L

/ = 1,2 — соответственно силы реза-

7 о7

1-1ППМВАЛAWI-lklA И ЧПАУТПИиАГУПМ ГТПППЫА ГАПАНЛАМГЛТАЛАМ" f * —    ¹¹ f * — ^{z z} _

Пг1х1, 11ии।ВС/ЦСГ1Г1 Die      leixi Uri"iek,ixUri Liuuunc к,еиви^цвг11 о ic/ieri, /    — ., . , , /

Le LML соответственно электромеханические постоянные времени серводвигателей вращения шпин-

DD

—(1) КА (2)^2

деля и подачи пиноли; Рэ1 = —, Тр =— — соответственно электрические постоянные вре мени серводвигателей.

Для изучения влияния процесса резания на свойства системы необходимо моменты М, (f)

представить в координатах состояния системы, то есть в координатах о^, оо₂. В свою очередь, угловые скорости вращения задают: скорость резания V_p, отличающуюся от со_х на коэффициент;

величину подачи S_p, которая связана со скоростью подачи V_s (t) = к_ред оо₂ (t) следующим интегральным преобразованием:

S,(t)=k„. J ^dt, t-T/2

где к№ — коэффициент, связывающий угловую скорость со скоростью подачи; Т— время одно го оборота, зависящее от со!.

Математическое моделирование сил в технологических режимах хорошо известно [5]. Оно основано на использовании экспериментального материала для установившегося состояния системы резания и представлено в виде известных эмпирических зависимостей. Однако эти зависимости не имеют ясного физического содержания, так как показатели степени в аппроксимируемых зависимостях являются дробными. Кроме того, они имеют ограниченную область определения и представлены не в координатах состояния, а в технологических режимах, которые отличаются соотношениями (3) [5-8]. Выполненные авторами экспериментальные исследования и параметрическая идентификация зависимостей сил от координат состояния о^ и о^ позволили пред ложить следующие зависимости сил от координат состояния системы

М_х (t) = ^«2 (tJexpf-^Wj (t)];

М2 (t) = к2 [w2 (t)]2 expf-^Ц (t)], где kY и k2 параметры, имеющие соответственно размерности [кгм-с] и [кгм-с2]; к^ и к^ — параметры, характеризующие крутизну нарастания моментов по мере уменьшения угловой скорости вращения шпинделя в [с]. В большинстве случаях можно считать, что t-t1) _ t-t1) _

Выражения (4) характеризуют следующие главные особенности представления сил в рассматриваемых координатах состояния: 1) по мере увеличения скорости резания при неизменной скорости подачи силы уменьшаются; 2) при увеличении скорости подачи силы возрастают, причём осевое усилие за счёт сближения задней грани инструмента с заготовкой возрастает непропорционально быстро; 3) функции (4) являются гладкими и дифференцируемыми необходимое число раз. Таким образом, динамика собственно процесса сверления описывается следующей системой:

, m f                 dw, с/оо₂11     / х d²№_{Y                        / x}

^K ^^Ш2 ‘Э ^К0^Ш2                                               ' ЭМ        ^{+ Ш}1 j /

/. X / f2) f 2     f2) /   2 dtoi ~ dto2 |      / , x             d Ш2 (t) -т-Г21 dto2 (t)       / x m 111 — Jr 1 2 mz — TV ' Jr mz____L —             I Avn i —Jr m 1 — TV 'TV >_____\   . T-ZV z v 7 m f 1

^Ш0,2 ^K |^Ш2  ' Э ^К0^Ш2 д ^ZU)2 д J ( ^К0^Ш1 j “ ЭМ Э ^2   ⁺ ЭМ д ⁺ V j

R к где к^ = 1 1 — безразмерный коэффициент; к^ = 2 2 — параметр, имеющий размерность времени.

Рассмотрим типичную осциллограмму изменения крутящего момента в процессе единичного заглубления при сверлении глубоких отверстий (рис. 1). На осциллограмме по мере заглубления инструмента в заготовку можно выделить следующие стадии:

• -    участок 0-1 соответствует переходному процессу изменения крутящего момента при врезании инструмента в заготовку;

  

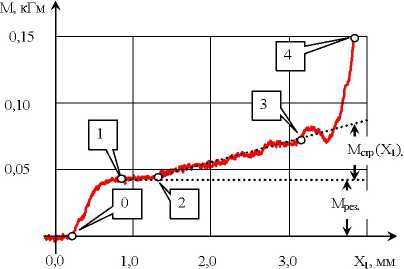
  Рис. 1. Пример осциллограммы крутящего момента в процессе единичного заглубления при сверлении топливоподводящего отверстия в корпусе форсунки диаметром 2,15 мм из стали 35Л

  
  

• -    участок 1-2 соответствует стационарному установившемуся процессу. Если бы не было накопления стружки в стружкоотводящих канавках сверла, то момент резания Мрев, оставался бы

неизменным при постоянных режимах и состоянии инструмента;

• -    участок 2-3 соответствует накоплению стружки в стружкоотводящих канавках. Здесь к моменту, формируемому в зоне резания Мрев., добавляется момент Метр (Ai), формируемый стружкой при её движении по стружкоотводящим канавкам. Этот момент пропорционально нарастает по мере заглубления. Поэтому его можно представить в виде интеграла от скорости подачи по

перемещению;

• -    участок 3-4 соответствует нестационарному увеличению крутящего момента. Здесь тра

ектория момента соответствует потере устойчивости стационарной траектории увеличения кру тящего момента.

Обычно пространственное запаздывание в накоплении стружки в стружкоотводящих канавках есть величина малая. Кроме того, накопление стружки мало влияет на осевое усилие. Поэтому с учётом накопления стружки система (5) несколько видоизменяется

< fit _ Т^

к-ш. ^~^ j-exPf-^i)-< Ij^ (^f)^л + Л"[ш, (f|-ш, (0)]}

(1, (1,ЛоД£)   (1,ЛоД£)

‘ ЭМ* Э ^2      ¹ ЭМ ^         )f

v              ^n^w2 — Л - 2оо.—- fexpt-^coj

• \    /         Z         U Z ^       Z д J \     1 /

~'ЭМ'Э ^2   ' ‘ ЭМ ^  ^Ш2^Л где кс — параметр, характеризующий интенсивность нарастания момента при накоплении стружки, в |^(мм • с)-1].

Таким образом, система (5) характеризует динамику процесса сверления, а система (6) дополнительно учитывает влияние накопления стружки на динамику системы.

Анализ результатов. Выполненное цифровое моделирование динамики системы процесса сверления и дополнительное влияние накопления стружки на траекторию изменения сил, скоростей и величин заглублений позволили выявить наиболее важные особенности системы.

Проанализируем особенности динамики системы (5) или соответствующей ей системы (1) с учётом (4). Рассмотрим свойство равновесия. Для этого необходимо проанализировать систему соО1 - к^юг ехр(-А-ооох) = оох; соО2 - ^^ool exp^/CoWj = о)2.

По мере варьирования ш_од и со_{о 2} система (7) может иметь одну (при малых значениях ш_од, go_O2) или три точки равновесия. На рис. 2 приведён пример смещения точек равновесия системы для о^ при изменении напряжения на якоре двигателя вращения шпинделя.

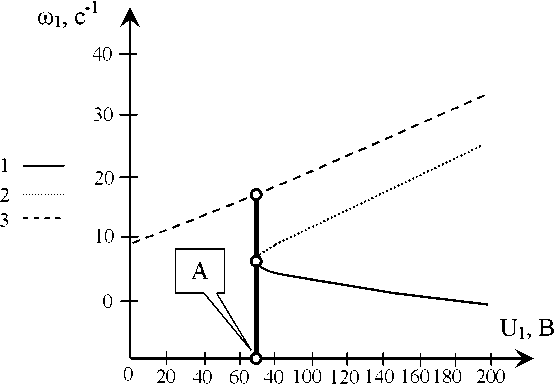
Рис. 2. Пример смещения точки равновесия двигателя вращения шпинделя при постоянном напряжении на двигателе подачи

Анализ линеаризованного уравнения в вариациях относительно рассматриваемых точек равновесия показал, что точечной ветви на приведённой диаграмме соответствует асимптотически устойчивое положение равновесия. Пунктирной и сплошной линии соответствует неустойчивая точка. Этот анализ показывает, во-первых, при варьировании напряжения якоря имеет место бифуркация равновесия типа вилки. На иллюстрации эта точка обозначена А. Во-вторых, асимптотически устойчивая в малом точка равновесия имеет ограниченную область притяжения, и она изменяется при варьировании шп, и ш

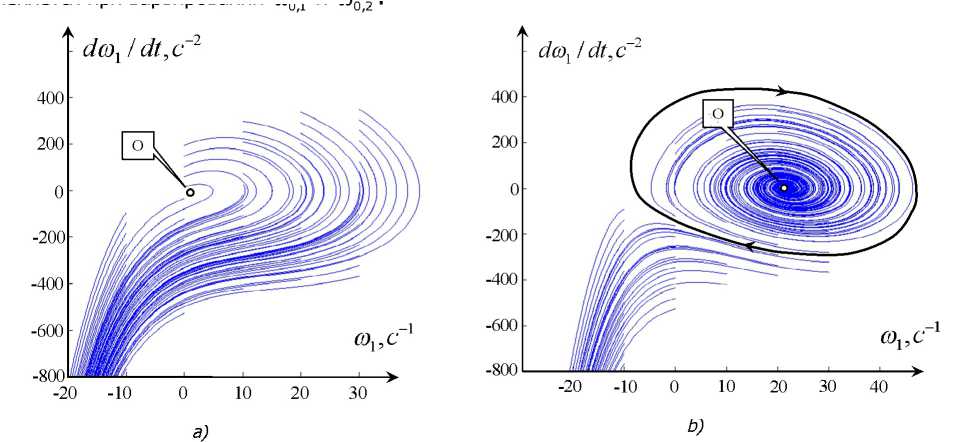
Рис. 3. Пример проекций фазовых траекторий на плоскость (ш_х, с/ш_х / dt\:

a— co_DX = Юс"¹; b— co_DX = 30с

Приведём также типичные проекции фазовых траекторий на фазовую плоскость (оо_1Л с/оз₁ ! dt^ (рис. 3). Здесь необходимо обратить внимание на то, что при малых значениях напряжения якоря двигателя шпинделя система является неустойчивой в целом, а при больших— устойчивой в малом. В последнем случае она имеет ограниченную область притяжения, зависящую от параметров двигателя и напряжения якоря при неизменных параметрах. Эта область ограничена сепаратриссной кривой, выделенной на рис. 3, b жирной линией.

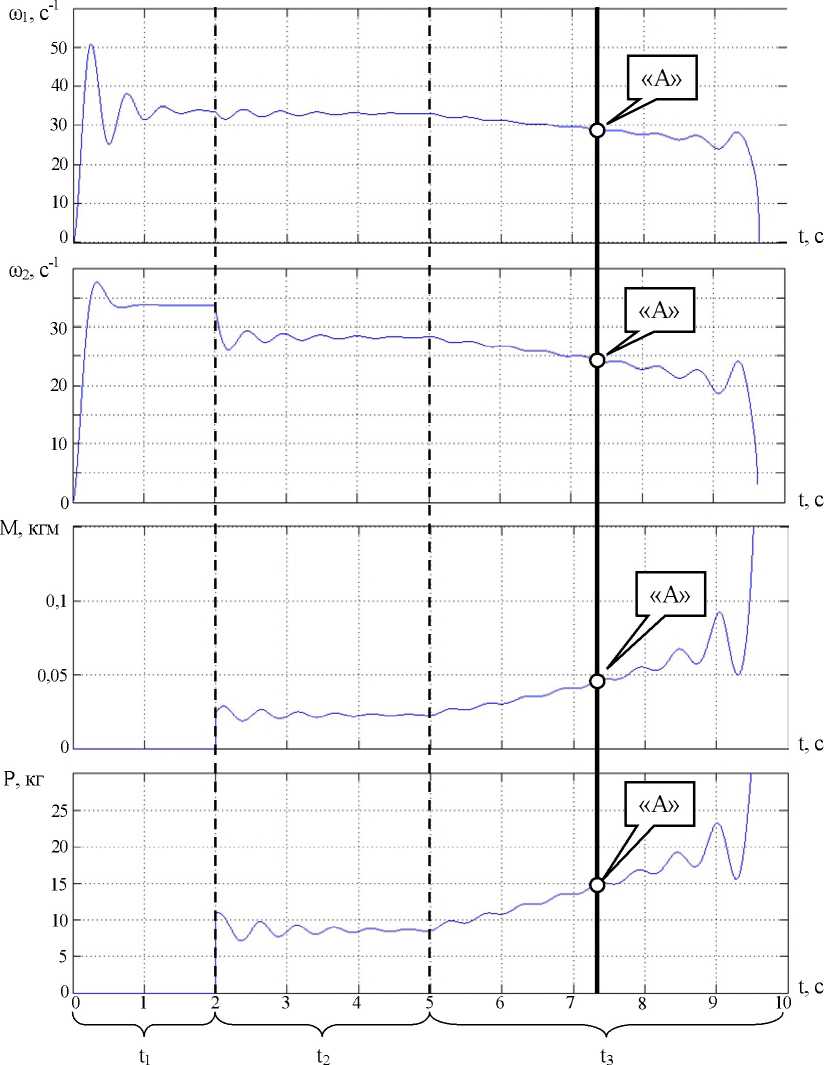
Рис. 4. Временные диаграммы скоростей двигателей вращения шпинделя и подачи в режиме имитации цикла процесса сверления: а — холостой ход (разгон и подвод сверла к области резания), а — врезание, 6 — сверление с неизменными режимами с учётом накопления стружки

Важно подчеркнуть, что в данном случае шод определяется напряжением якоря двигателя и моментом, действующим на инструмент, но не связанным непосредственно с процессом резания. Например, моментом, формируемым стружкой, которая накапливается в стружкоотводящих канавках. Поэтому при использовании уравнения (6), учитывающего интегрирующее по пути заглубления инструмента влияние стружки, наблюдается динамическая перестройка системы. При этом, как правило, суммарное значение шод достигает таких значений, при которых система теряет устойчивость. Это соответствует точке 3 на рис. 1. Приведём пример изменения координат состояния системы во времени, которое соответствует системе (6) (рис. 4). Здесь необходимо отметить потерю устойчивости траектории изменения сил и скоростей в точке А. Подчеркнём, что не только качественно, но и количественно кривые изменения сил соответствуют экспериментальным результатам, приведённым на рис. 1. Таким образом, важный механизм заклинивания инструмента при сверлении глубоких отверстий связан с потерей устойчивости рассматриваемых стационарных траекторий.

Для пояснения механизма заклинивания и поломок инструмента удобно рассмотреть совместную диаграмму изменения угловых скоростей серводвигателей (рис. 5), на которой можно выделить область режимов, которым соответствует предельное значение момента, действующего на инструмент. Эта область определяется по зависимостям (7).

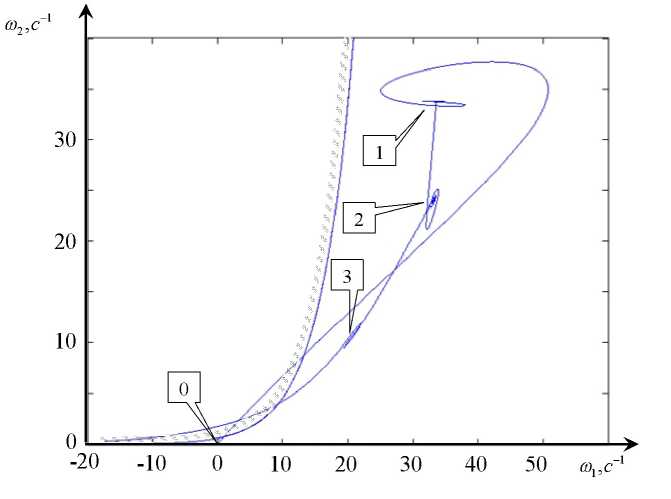
Рис. 5. Отображение области предельных значений крутящего момента в плоскости (coL, ш2)

На приведённой диаграмме участок траектории 0-1 соответствует запуску двигателей без контакта инструмента с процессом резания, участок траектории 1-2 соответствует переходному процессу при врезании инструмента в заготовку, участок траектории 2-3 соответствует изменению скоростей по мере накопления стружки в стружкоотводящих канавках. В точке 3 система теряет устойчивость. В результате координаты состояния достигают значений, при которых крутящий момент приобретает критическое значение. При изменении параметров двигателя и (или) динамической характеристики процесса резания область траекторий без поломок существенно меняется. В заключение отметим, что параметры серводвигателей можно варьировать в достаточно широком диапазоне на основе введения в двигателях дополнительных связей. Например, если измеримыми являются ток и угловая скорость, то за счёт введения дополнительных связей можно рассматривать уравнение, например, двигателя вращения шпинделя в следующем виде:

j =с^№1 -М (tV

‘                                                                                     (8)

Таким образом, в (8) противо-ЭДС уже определяется коэффициентом (с^ +Агш), а сопротивление якоря двигателя — коэффициентом (Rt + к,). Подчеркнём, что коэффициенты к, и кю могут варьироваться в достаточно больших пределах.

Заключение. Динамические свойства серводвигателей вращения шпинделя и подачи пиноли в силовых сверлильных головках существенно влияют на динамику системы сверления глубоких отверстий. При этом два привода вращения инструмента и подачи через динамическую связь, формируемую процессом обработки, объединяются в единую связанную динамическую систему. В данной системе формируемая динамическая связь выступает в роли внутреннего регулятора, в котором силы зависят от траекторий и, следовательно, влияют на сами траектории. Можно выделить два противоречивых фактора влияния сил зависящих от траекторий. Во-первых, при увеличении сил наблюдается уменьшение угловой скорости вращения шпинделя из-за конечной жёсткости механической характеристики двигателя. Следовательно, в этом случае силы увеличиваются. Во-вторых, по этой же причине при увеличении сил уменьшается скорость подачи. Следовательно, силы уменьшаются. Это противоречивое влияние позволяет за счёт выбора, например, передаточного отношения редуктора в приводе подачи (оно во многом определяет коэффициент к^ в (4)) обеспечить взаимную компенсацию влияния сил на траектории движения. При этом удаётся существенно увеличить величину единичного заглубления. Кроме того, приведённые модели и выполненные исследования показывают, что за счёт выбора параметров местных обратных связей можно существенно изменять динамические свойства и величину единичного заглубления при сверлении без поломок инструмента.