Влияние параметров текстуры на устойчивость процессов формоообразования анизотропных заготовок

го использования направленности свойств заготовок необходимо на основе кристаллографического подхода рассмотреть влияние параметров текстуры и констант кристаллической решетки на устойчивость процессов формообразования.

Можно отметить три типа потери устойчивости в процессах формообразования высокотекстурированных материалов: образование полос скольжения на поверхности вытягиваемых заготовок, появление складок и шейкообразование[4]. Наибольший интерес для анализа процессов формообразования деталей сложной формы представляет потеря устойчивости третьего типа, которая возникает в момент, соответствующий достижению наибольшего усилия на диаграмме растяжения.

Причина потери устойчивости в этом случае заключается в уменьшении сопротивления деформирования элемента заготовки, вызываемом уменьшением его площади поперечного сечения и модуля упрочнения. Заготовка теряет устойчивость после достижения критических деформаций, т.е. в некоторой области очага деформаций появляется значительная сосредоточенная деформация и происходит разрыв.

Рассмотрим процесс двухосного растяжения прямоугольного листа из ортотропного материала толщиной w в условиях плоского напряженного состояния ( СТ 3 — 0 ).Обозначим через р усилие, приложенное к элементу листового материала и направленное по оси u , а через Q – усилие, действующее вдоль оси v . Криволинейные координатные линии u и v выбраны так, чтобы они совпадали с траекториями главных нормальных напряжений O "i и (Т ^, а также с главными осями анизотропии (рис. 1).

Тогда нагрузки на лист P и Q равны:

P — O 1 NVW И Q — ^kuw . (1)

В процессе штамповки эти усилия будут возрастать в результате упрочнения металла и

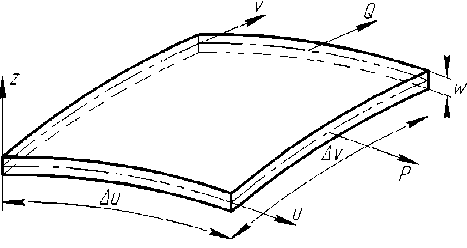
Рис. 1. Элемент листовой заготовки, находящийся в двухосном напряженном состоянии

Для того чтобы учесть влияние ориентационных факторов текстуры A,■ и констант кристаллической решетки S ijkl на потерю устойчи-востив случае сосредоточенной (местной) де-формациивоспользуемсякритерием пластичности,предложенными в работе [6]. Тогда для плоского напряженного состояния ( C 3 = 0 )получим следующие выражения для интенсивности напряжений:

уменьшаться вследствие уменьшения размеров элемента. Равновесие будет устойчивым, если изменение деформирующей силы вызывает малое изменение деформации. Потеря устойчивости определяется условием максимума деформирующих усилий. Когда одно из усилий, приложенных к деформируемому элементу, достигает максимума, то дальнейшее возрастание деформаций происходит без увеличения усилия и может оказаться большим. Условие устойчивости имеет вид:

dP = dc,Avw + c,d (Av) w + c,Avdw > 0,

dQ = dc2Auw + с2d (Au)w + с2Audw > 0 (2)

Разделив каждое уравнение системы (2) на c , vw и C 2 uw соответственно, имеем:

C = V? ^(^12 ' )C1 ” 2^12C1C2 + +('2 +П23 )с2}Г2 ;

приращения интенсивности деформаций (с учетом условия несжимаемости):

V ' < 3 %i )

+2 dEd2 ЗД

или

dEi)

—+—

' 2 < 23 )

П 31

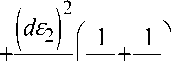
%3   'A' %1)

+

и уравнений связи деформаций и напряжений:

■ dC i + d W + dw >  0, C i     A v    w

C + d^ + dw >0

C 2     A u    w

dEi = ^dEL[('i2 + '3i )Ci -'i2C2], 2 C

dE2 = ^d^^[('i2 + '23 )C2-'i2Ci], 2 C

dE3 =-

i dE i

^{2 C} i

[ ' 3i ^C i ⁺ ' 23 ^C 2 ] ,

---^{1 +} d ^E 2 ⁺ d ^E 3 >  0,

C de2            n

--+ d e , + d E 3 >  0

I ^C 2

где dE i , d^ 2 и d^£ 3 - приращения главных деформаций.

Используя условие несжимаемости материала ( dE i + d^ 2 + d^£ 3 = 0 ), условие положительности добавочных нагрузок можно записать в виде:

где Ijy = ( Q ^{+ A} k ^-A i ^-A j )/ ( Q ^- V5 ) — обобщенный показатель текстурированного состояния материала;

Q =⁽ ^ Hii ^- S'\ i22 У(³ S I iii ^-3 S I i22 ^-32 S 2 323

характеристический параметр кристаллической решетки.

Введемвеличину, характеризующую напряженное состояние:

C

da ,                                  m = ^,            zq\ ar" > dEi,                                          с,                (9)

^: d e                  (5) тогда выражение для определения величины

---2 > dE2                  интенсивности напряжений (6) преобразуется к с 2                          виду:

^r V2    ^+%1 ) ^- " ^{m +} " ' " 2 3 ^ ^m ° 1.(10)

Установим связь между интенсивностью деформаций d£ и d£ , d^ 2, d£ 3 .Для этого из системы (8) с учетом зависимости (9) выразим:

d£2 — m("12 + "23)-"12("12 + "31)- т"12

изменяется, т.е. dm|d£ i — 0 , а значит,между приращениями деформаций наблюдается линейная зависимость типа d£ 1 — const d£ 2 . Она будет иметь место и при конечных деформациях, если ориентационные факторы текстуры А , сохраняют свое значение, т.е. при d" y Jd £ , — 0 . С учетом сказанного неравенства (14) упрощаются и принимают следующий вид:

Тогда, подставляя полученное выражение (11) в (7), окончательно получим:

, _ ( " 12 ⁺ " 31 ) ^- " 12 ^m ,

d £1 —-----------------d £,

dri > ("12 + Л31 )-"12т rid£i           K rid£i           K

K

- d^ — ^ " 1 d£ , 3 _Ki

K — V2^(^12 + "31 )- "т + (^12 + "2 3) т2 .

Решив уравнение (11) относительно показателя напряженного состояния m , получим формулу, которая позволяет определить величину m экспериментально, путем замера деформаций, например, с помощью координатной сетки:

Из системы (15) легко получить зависимость критической деформации от параметров текстуры А i и показателя напряженного состояния т , если известна кривая течения материала. Зависимость между интенсивностями напряжений и деформаций может быть аппроксимирована степенной функцией:

Г — С£ ” , (16) где C и n определяются из опыта на растяжение. Эта аппроксимация достаточно точно выражает действительную зависимость между напряжениями и деформациями[1].

Дифференцируя уравнение (16), найдем:

d ^ i- — Cn £ ^{n - 1 d £} i

n

— 7Gi £i

( " 12 ⁺ " 31 ) ^d£ 2 ⁺ " 12 ^d£ 1 т —-----------------

Подставляя соотношения (10) и (12) в неравенства (5), получим:

Подставляя зависимость (17) в систему (15), получим наибольшее значение величины устойчивости интенсивности деформаций, которая может быть реализована в процессах формоизменения высокотекстурированного материала:

dmdm

N- " — + 2("12 + "23 ) т d г,          d £ rid^i

dm           dm dr, > N + " d" - 2<"12 +^31)т5£- rid£              K2

K

N—

d"12 ₊ d" 31 d£ d£

- 2 d"!2 т+ d£

d’12 + d"23 d£i   d£i v

.

При простом нагружении отношение компонент напряжений в процессе деформирования не

кр

^£ i

кр i

K

( " 12 ⁺ " 31 ) ^- " 12 ^т

K

Критической является наименьшая из деформаций условия (18), взятая со знаком равенства. Рассмотрим случай, когда | o "1| > | г 21, т.е. двухосное напряженное состояние потеряет устойчивость при нарушении первого из неравенств (18), подставив которое в уравнения (12), получим критические деформациипри простом нагружении:

кp

£1

кp

£2

— n

_— ( " 12 ⁺ " 23 ^{) т -} " 12 _n ( " 12 ⁺ " 31 ^)- " 12 ^т

_{- £} кр _—     "  23 ^{т +} "  31     n

³     ( " 12 ⁺ "  31 ^)- " 12 ^т

Как видно из формул (18) и (19), способность высокотекстурированного материала к пластическому формоизменению зависит от характера напряженного состояния, которое определяется величиной m , модуля упрочнения n , характеризующего способность материала к упрочнению, а также параметров текстуры A i , определяющих анизотропию и текстурированное состояние материала.

Из табл. 1, где приведены результаты расчетов по формулам (18) и (19), следует, что в отличие от изотропного материала, наибольшая равномерная деформация по толщине которого может быть реализована только в условиях равномерного двухосного растяжения при m = 1 , процесс пластического формоизменения высокотекстурированного материала можно интенсифицировать даже при простом одноосном растяжении путем создания эффективной анизотропии свойств.

На рис. 2 показаны зависимости критических деформаций е К от характера напряженного состояния m для различных кристаллографических ориентировок. Например, для ориентировки {230}<231>при m = 1 величина критической деформации, показанная на кривой 3, составляет е К = 3,86 n , в то время как для изотропного металла (кривая 2) при тех же условиях эта величина равна 2 n . При других параметрах текстуры критическая деформация может оказаться меньшей, чем для изотропного металла (кривая 1).

При анализе устойчивости двухосного напряженного состояния по формулам (18) и (19) принималось, что усилие воспринимается одним определенным элементом, деформирующимся в процессе формообразования. Однако, возможен случай, когда ширина элемента, через который передается усилие в момент потери устойчивости, является постоянной. Полагая на этом основании в первом неравенстве системы(3) d (Av) — 0, получим условие устойчивости:

М

~ ^{- d £} 3 .          (20)

Тогда критические значения деформаций с учетом выражений (10), (12) и (17), а также принятого допущения о простомнагружении, примут вид:

е р <---- K---- _п , Т / 23 m ⁺ / 31

кр  ( / 12 ⁺ / 31 ) ^- / 12 m

• 1    =------------------- n

  / 23 ^{m +} / 31

кр _ ( / 12 ⁺ / 23 ) ^{m -} / 12

• 2    =                     n

  / 23 m ⁺ / 31

-£pP = П

В табл. 2 приведены значения деформаций, вычисленные по формулам (21). В этом случае процесс формообразования отличается большей устойчивостью. При m = - ^ 31 /7 / 23 устойчивость получается неограниченной, и процесс формообразования может продолжаться без локализации до полного исчерпания пластичности.

Значения критических деформаций в табл. 12 представляют собой их пределы, определяемые только устойчивостью процесса. Эти значения могут быть реализованы, если пластичность деформируемого материала достаточна.

Для оценки локального деформированного

Таблица 1. Величины критических деформаций при | С 1| >

m	кр e i	( е 1 p ) кр	( е Р ) кр	( е Р ) кр
- 1	у 2 74 / 12 + / 23 + / 31 n 2 / 12 + / 31	n	2 / 12 + / 23 и П 2 / 12 + / 31	;; ^2+ ; :, п
- 0,5	^2 79 / 12^ / 23+^ / 31 n 3 / 12 + 2 / 31	n	- 3 / 12 + / 23 n 3 / 12 + 2 / 31	: :,';:й,.
0	2 n	n	/ 12    П	/ 31
	7 / 12 + / 31		/ 12 + / 31	/ 12 + / 31 ”
0,5	^ 7 / 12 + / 23 + 4 / 31 n / 12 + 2 / 31	n	- / 12 - / 23 n / 12 + 2 / 31	/ 23 + 2 / 31 П / 12 + 2 / 31
1	^/2 7 / 23 + / 31 n / 31	n	^ 23 П / 31	/ 23 + / 31 и П / 31

Таблица 2. Величины критических деформаций при d ( A v ) = 0

m	кр fc i	p кр ( Ч j	p кр \Ь2 j	p кр ( fc 3 j
- 1	^ У 4 ^ 12 + ^ 23 + ^ 31 n 7 31 -%3	2 7 12 + 7 31 „ n 7 23 - 7 31	2 7 12 + 7 23 n 7 23 - 7 31	- n
-0,5	^ У9 7 12 + 7 23 + 4 7 31 n 2 7 31 - ^ 23	37 2 + 2 7 31 и n 7 23 - 2 7 31	3 7 12 + 7 23 n 7 23 - 2 7 31	- n
0	У 7 12 + 7 31 n 7 31	7 12 + 7 31 n 7 31	7 2 —— n 7 31	- n
0,5	^ У 7 12 + ^ 23 + 4 7 31 n 7 23 + 2 7 31	7 12_ ±2 7 31 n 7 23 + 2 7 31	- 7 12 -7 23 n 7 23 + 2 7 31	- n
1	2 n У%3 + 7 31	7 31   П 7 23 +7 31	7 23   n 7 23 + 7 31	- n

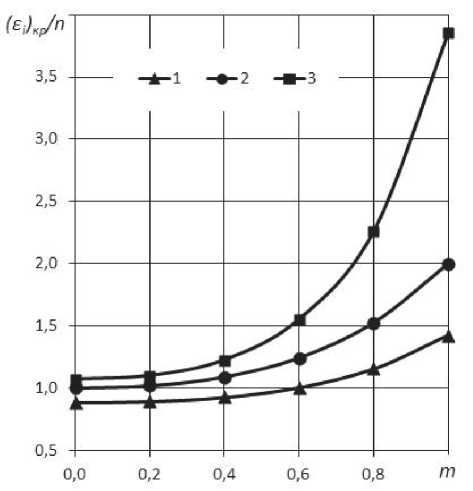
Рис. 2. Зависимость критической деформации анизотропного листового металла от напряженного состояния и параметров текстуры: 1 - A ₁ = 0,09, A ₂ = 0,270, A 3 = 0,274({133}<130>);

2 - A i = A 2 = A з = 0,2 (изотропная среда); 3 - A ₁ = 0,25, A ₂ = 0,067, A ₃ = 0,213 ({230}<231>)

состояния воспользуемся коэффициентом локального использования пластичности [4]:

^e i

V крр ,              (22)

fci который показывает во сколько раз локальная накопленная интенсивность деформаций меньше критической. При у = 1 возникает опасность появления разрывов листовой заготовки.

Устойчиво формообразование идет при запасе пластичности ~ 20%, т.е. у = 0,8 , при котором компенсируются изменения механических характеристик одной партии металла и условий штамповки.

ВЫВОДЫ

• 1.    Разработана запись критерия устойчивости процесса формообразования анизотропных заготовок, учитывающая в явном виде кристаллографическую природу анизотропии свойств через ориентационные факторы текстуры и константы кристаллической решетки металлов.

• 2.    Анализ полученных соотношений показал, что, управляя составом текстуры, т.е. набором кристаллографических ориентировок и их весовыми долями, можно значительно повысить степень предельного деформирования ортотропного анизотропно-упрочняющегося материала в условиях плоского напряженного состояния.