Влияние переменного магнитного поля на динамику положения равновесия прецессии намагниченности в изотропной магнитной пленке

Исследованию нелинейной динамики магнитной, упругой и магнитоупругой подсистем в ферритовых пленках посвящено значительное количество работ [1–4]. С появлением материалов с высокой добротностью, в первую очередь железоиттриевого граната (ЖИГ) [5], было установлено, что нелинейные явления, имеющие место при крайне малых амплитудах прецессии намагниченности, затрудняют проявление нелинейных процессов, происходящих при больших углах раскрытия конуса прецессии. Данную проблему можно решить путем выбора соответствующей геометрии образца, а именно плоскопараллельной перпендикулярно намагниченной пластиной. При этом частота однородной моды ферромагнитного резонанса приходится на дно спектра обменных спиновых волн, вследствие чего их параметрическое возбуждение становится невозможным.

В работе использована система уравнений, аналогичная представленной в [6] и описывающая электромагнитное нелинейное возбуждение магнитоупругих колебаний в нормально намагниченной пластине, когда параметрическое возбуждение спиновых волн не осуществляется. В работе исследуется только первая упругая мода, а возмущающее переменное поляризованное по кругу поле ориентировано в плоскости пластины.

Геометрия задачи и основные уравнения

В статье рассматривается бесконечная ферритовая пленка, намагниченная по нормали к ее плоскости (см. рис. 1). При этом резонансная частота колебаний намагниченности соответствует дну спектра обменных спиновых волн, что исключает их параметрическое возбуждение. При этом прецессия вектора намагниченности может происходить с отклонением от нормали к плоскости пленки на угол более 10°. Возбуждение колебаний осуществляется посредством приложенного поляризованного по кругу поля, плоскость поляризации которого параллельна плоскости пластины. Задача решается в декартовой системе координат Oxyz . Оси координат параллельны рёбрам куба кристаллографической ячейки. Центр системы координат O совпадает с центром пластины.

Полагая полную плотность энергии пленки U в поле H = { h x ; h y ; H 0 }, равной сумме плотностей магнитной, упругой и магнитоупругой энергий, получим

M_oh_ym_y — M_oH_om_z + 2^M ^ m z

U = — M_oh_xm_x

—

+ ²С 44 (^ ху + ^u yz + ^u zx ^ +

+2S₂ (m_xm_yu_xy + m_ym_zU y _Z + m₂m_xu_zx) , (1) где m = M / M 0 – нормализованный вектор намагниченности, M 0 – намагниченность насыщения плёнки, u ij – компоненты тензора деформаций, c 44 – упругая константа, B 2 – магнитоупругая константа.

Рис. 1. Геометрия задачи.

Fig. 1. Geometry of the task.

Колебания намагниченности и упругого смещения определяются уравнением Ландау-Лифшица с диссипативным членом в форме Гильберта и уравнением для компонент вектора механических смещений:

^ = ^—y[m x H_eff\ + a[m x ^^\ , 9²U_Xy =- _2R ^^ихУ I £ 44 _ ^ ² ^■xy dt²             dt p dz² ’

где γ – гиромагнитное отношение, α , β – константы затухания для магнитной и упругой подсистем, соответственно.

Эффективные поля определяются следую- щим образом:

- _—2_ . ^L ^eff     M_o dm ^.

Граничные условия: duxy

^!'-- .Z _z ,^ ₂ = ^— B 2 ^m xy ^m z -

Система уравнений (2–3) с граничным условием (5) решалась численно методом Рунге-Кутты 7–8 порядка с контролем точности на каждом шаге.

При расчете использовались параметры материа- ла, типичные для пленки Ni: M0 = 440 Гс, H0 =

5500 Э , параметр затухания магнитной подсистемы равен α = 0.035 , напряженность компонент переменного поля с круговой поляризацией, лежащей в плоскости Oxy , составила h 0x = h 0y = (0 ÷ 1.5) · 10³ Э при частоте переменного поля, равной ω 0 = 9 · 10¹⁰с^-1 .

Динамика прецессии положения равновесия

На рис. 2 представлены зависимости динамики вектора намагниченности от амплитуды переменного поля для изотропных пленок. Они позволяют выявить четыре основных режима прецессии вектора намагниченности, последовательно сменяющих друг друга с ростом амплитуды переменного магнитного поля. При амплитуде переменного поля h 0 → 0 реализуется режим А (рис. 2а) – малоамплитудная круговая прецессия, при амплитуде переменного поля (20 ≤ h 0 ≤ 950) Э реализуется режим B (рис. 2b) – прецессия положения равновесия без охвата центра, при ( 950 ≤ h 0 ≤ 1150 ) Э – режим С (рис. 2c) – прецессия положения равнове-

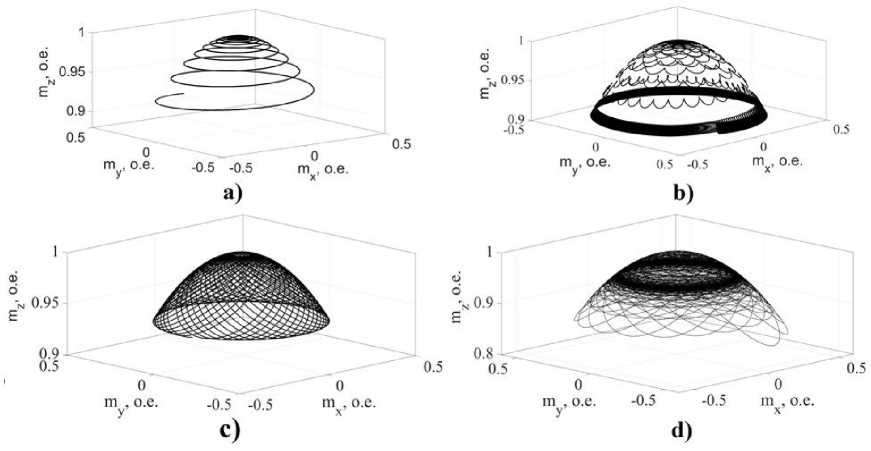
Рис. 2. Режимы прецессии вектора намагниченности: (а) – малоамплитудная круговая прецессия при h₀ = 1 Э ; (b) — прецессия положения равновесия без охвата центра при h₀ = 75 Э ; (c) - прецессия положения равновесия с охватом центра при h₀ = 10³ Э ; (d) - затухающая прецессия положения равновесия при h₀ = 1.5 • 10³ Э .

Fig. 2. Precession modes of the magnetization vector: (a) - low-amplitude circular precession at h₀ = 1 Oe ; (b) -precession of the equilibrium position without the coverage of the center at h₀ = 75 Oe ; (c) - precession of the equilibrium position encompassing the center at h₀ = 10³ Oe ; (d) - damped precession of the equilibrium position at h₀ = 1.5 • 10³ Oe .

сия с охватом центра. Дальнейшее увеличение амплитуды переменного магнитного поля приводит к колебаниям вектора намагниченности в режиме D (рис. 2d) – затухающая прецессия положения равновесия.

Амплитудно-частотные характеристики колебаний вектора намагниченности в указанных режимах представлены на рис. 3. Из него (рис. 3а) видно, что неустойчивость, расположенная в области низких частот, сужена и смещена в нулевую об-

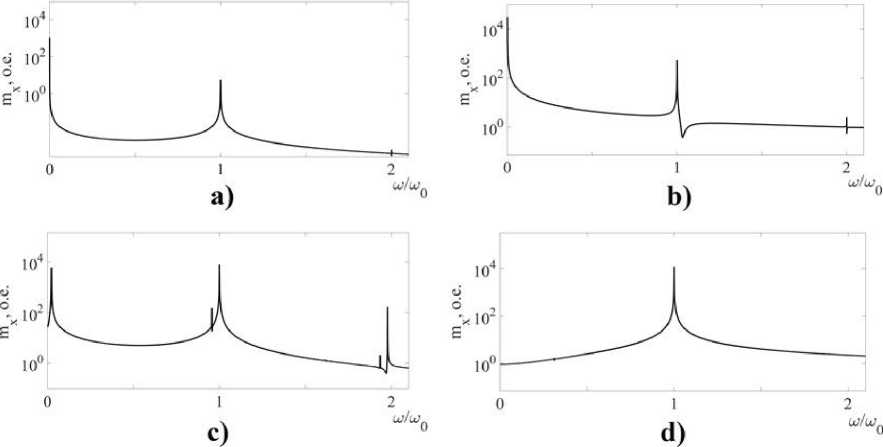
Рис. 3. Амплитудно-частотные характеристики режимов прецессии вектора намагниченности: (а) – мало-

амплитудная круговая прецессия при h₀ = 1 Э ; (b) - прецессия положения равновесия без охвата центра при h₀ = 75 Э ; (c) - прецессия положения равновесия с охватом центра при h₀ = 10³ Э ; (d) - затухающая прецессия положения равновесия при h₀ = 1.5 • 10³ Э .

Fig. 3. Amplitude-frequency characteristics of the precession modes of the magnetization vector: (a) – low-amplitude circular precession at h₀ = 1 Oe ; (b) - precession of the equilibrium position without the coverage of the center at h₀ = 75 Oe ; (c) - precession of the equilibrium position encompassing the center at h₀ = 10³ Oe ; (d) -damped precession of the equilibrium position at h₀ = 1.5 • 10³ Oe .

ласть. Это означает сильное уменьшение частоты осцилляций положения равновесия вектора намагниченности, при этом амплитуда этих колебаний на порядок больше амплитуды колебаний намагниченности на частоте переменного поля ω 0 .

На рис. 3b, представляющем амплитудночастотную характеристику колебаний компоненты намагниченности m x в режиме прецессии положения равновесия без охвата центра, видно, что непрерывный спектр в области низких частот незначительно изменяется. Область настойчивости, находящаяся вблизи нулевой отметки, смещается вправо, что говорит об увеличении частоты колебаний прецессии положения равновесия. Амплитуда колебаний на частоте переменного поля резко возрастает на порядок и составляет не менее 10 % амплитуды колебаний на прецессии положения равновесия.

Амплитудно-частотная характеристика прецессии положения равновесия с охватом центра, представленная на рис. 3с, указывает на перераспределение энергии между колебаниями прецессии положения равновесия и колебаниями на частоте переменного поля. При этом в области низких частот спектра пик, соответствующий колебаниям положения равновесия, имеет амплитуду меньшую по величине амплитуды колебаний намагниченности на частоте переменного поля.

Анализ спектров колебаний намагниченности после установления стационарных колебаний в режиме D – затухающая прецессия положения равновесия, представленных на рис. 3d, позволяет сделать вывод о прекращении прецессии положения равновесия за счет затухания колебаний прецессии положения равновесия.

Дальнейшее увеличение амплитуды переменного поля приводит к уменьшению времени достижения стационарного состояния прецессии вектора намагниченности, за счет быстрого затухания прецессии положения равновесия. Прецессионный портрет принимает вид узкого кругового кольца, диаметр которого плавно возрастает по мере увеличения амплитуды переменного поля.

Зависимость частоты прецессии положения равновесия от амплитуды переменного магнитного поля показывает (рис. 4), что с ростом амплитуды переменного поля частота прецессии положения равновесия увеличивается до значения h 0 = 800 Э. После чего начинает монотонно уменьшаться до значения переменного поля, равного 1050 Э, что достаточно точно описывает изменения амплитудно-частотных характеристик колебаний вектора намагниченности при смене режимов прецессии и отмечено на рис. 4 областью (I). В области (II) (см. рис. 4), соответствующей затухающей прецессии положения равновесия, наблюдается рост частоты прецессии положения равновесия вектора намагниченности при значениях амплитуды переменного поля в диапазоне (1100 ≤ h 0 ≤ 1650) Э .

В рамках настоящей работы авторы не ставили задачу полностью исчерпывающего исследования описываемых явлений, а старались предста-

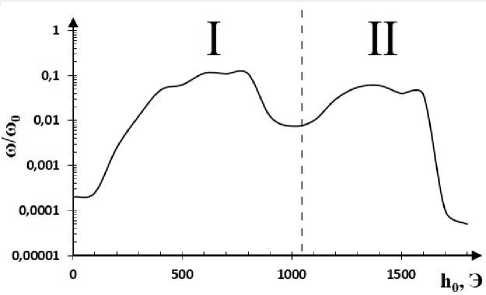
Рис. 4. Зависимость частоты прецессии положения равновесия от амплитуды переменного магнитного поля.

Fig. 4. Dependence of the precession frequency of the equilibrium position on the amplitude of the alternating magnetic field.

вить лишь общую картину в их совокупности. Вопрос причины увеличения частоты прецессии положения равновесия в области (II) авторы оставляют в качестве предмета для дальнейших исследований. Однако в качестве основной причины можно предположить возникновение колебаний с комбинационными частотами, вызванных областью неустойчивости на удвоенной частоте возмущения ω = 2 · ω 0 .

Заключение

В данной работе рассмотрены особенности поведения магнитной подсистемы ферритовой плёнки при воздействии переменного поляризованного по кругу магнитного поля. Получены зависимости развития колебаний вектора намагниченности от амплитуды переменного магнитного поля. Обнаружены колебания намагниченности на частотах прецессии положения равновесия, частоте переменного поля и частоте ФМР во всех режимах при возбуждении пленки переменным магнитным полем, лежащим в плоскости пленки. Определена область амплитуд переменного поля, при которой возможно возбуждение колебаний прецессии положения равновесия. Выявлено смещение частоты колебаний прецессии положения равновесия вектора намагниченности в область высоких частот, обусловленное влиянием удвоенной частоты возбуждения.