Влияние положения несущих консолей на аэродинамические характеристики амфибийных платформ

Одним из приоритетных направлений, озвученных руководством нашей страны – освоение Антарктики, Арктики с их богатыми месторождениями нефти и газа, развитие Крайнего Севера. Реализация данного проекта невозможна без построения мощной транспортной системы, основу которой должны составлять бесконтактные транспортные аппараты, такие как экранопланы и транспортные амфибийные платформы (ТАП), не требующие создания мощной инфраструктуры в виде дорог, аэродромов, пристаней.

ТАП – судно (летательный аппарат), использующее для своего поддержания на ходу и без хода преимущественно аэростатические силы, возникающие при направлении струи воздуха от движителей в пространство между крылом или корпусом судна и по- верхностью моря (суши) и их частичном или полном торможении (эффект поддува) [1]. Это принципиально новый тип аппарата с динамическим принципом поддержания является промежуточным между судами на воздушной подушке и экранопланами и объединяет в себе лучшие их качества (рис. 1). ТАПы более просты, надежны и экономичны чем экранопланы.

По отношению к аппаратам на воздушной подушке они имеют следующие преимущества: вдвое большую скорость; лучшую устойчивость на курсе при боковом ветре; отсутствие гибких ограждений и простоту конструкции, существенно повышающие надежность, удешевляющие эксплуатацию, технические обслуживание и ремонт; более высокую мореходность.

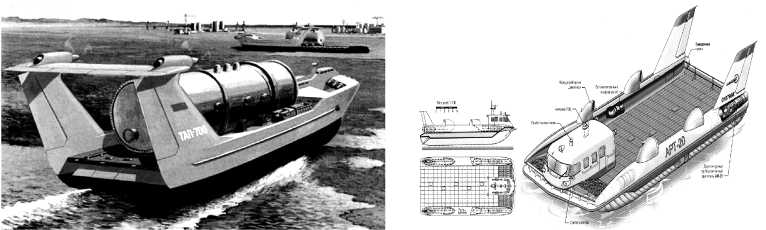
а

б

Рис. 1

На сегодняшний день ТАПы разрабатываются ЦКБ по СПК им. Р. Е. Алексеева: ТАП-30, ТАП-120, ТАП-150, ТАП-300, ТАП-500, ТАП-700 (рис. 1, а ) грузоподъемностью от 10 до 300 т, мореходностью от 1,0 до 2,5 м, и ЗАО «Амфибийные транспортные технологии»: «Акваглайд-60», «Акваглайд-200», АРТ-20 (рис. 1, б), представляющие собой платформу с под-дувной системой для создания подушки подобно эк-ранопланам «Орленок», «КМ», «Лунь» и др.

К недостаткам ТАП необходимо отнести постоянный контакт с подстилающей поверхностью, что приводит к повреждению амортизирующих взлетнопосадочных устройств - баллонетов-скегов - и ограничение мореходности при волнении. Кроме этого необходимо отметить, что при крейсерском режиме движения доля экранного эффекта, реализуемого на транспортной платформе, на сегодня составляет не более 20 %. Все эти указанные недостатки не обеспечивают высокие технико-экономические показатели транспортных амфибийных платформ.

Улучшить транспортную эффективность ТАП и повысить мореходные качества при волнении можно выполнив платформу в виде компоновки «составное крыло», предложенной в 1970-х гг. Р. Е. Алексеевым, с целью максимальной реализации экранного эффекта на консолях и эффекта поддува на центроплане, а также обеспечив устойчивость как вблизи экрана, так и вне его пределов.

Остается открытым вопрос о том, как влияет вынос консолей в горизонтальной и вертикальной плоскостях относительно центроплана, наличие угла поперечного V консолей, шайб на аэродинамические характеристики всей несущей системы в целом и как определить числовые значения основных аэродинамических характеристик: коэффициента подъемной силы, продольного момента и индуктивного сопротивления.

Основной целью исследования являлось изучение влияния выноса консолей в горизонтальной плоскости относительно центроплана, при этом необходимо было решить следующие задачи:

• -    получить функциональные зависимости аэродинамических коэффициентов c_y = f (a, h ), m z = f (a, h ), c xi = f (a, h ) составного крыла;

• -    определить рациональное положение консолей, позволяющее получить максимальное значение коэф-

• фициента подъемной силы и аэродинамического качества при проектировании ТАП.

Решение задач проходило в два этапа:

• 1)    построение функциональных зависимостей c y = f a), m z = f a), c xi = f a) компоновки «составное крыло» вне экрана и c y = f (a, h ), m z = f (a, h ), c xi = f (a, h ) вблизи экрана в первом приближении и сингулярного интегрального уравнения несущей поверхности;

• 2)    численное решение данного уравнения панельным методом - определение числовых значений c y ( a, h ), m z (a, h ), c xi (a, h ) в зависимости от положения консолей.

Перейдем к рассмотрению каждого этапа.

Для получения функциональных зависимостей c y = f a), m z = f a), c xi = f a) компоновки «составное крыло» вне экрана, каждая консоль, включая центроплан, заменялась П-образным вихрем постоянной циркуляции (рис. 2).

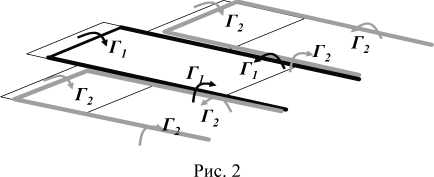
На основе закона Био-Савара учитывалось влияние свободных и присоединенных вихрей элементов несущей поверхности в виде средних дополнительных индуцированных углов:

- центроплана:

i 12

С 1     l 1 ^/2

c y 2 ¹ 21 ⁸ⁿX 1 - / ' /2

+

+

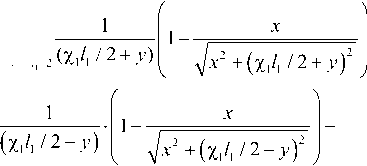
_____________1_____________

(X 212 + X1 V2 + У)

^^^^

dy ,

1            1                    x

+--1--                                   2

^X 2 1 ₂ + ^{X 1} l ¹ / ² - ^y ^   ^ x ² + ( X 2 / 2 +X 1 / 1 /2 - y )

- консолей:

1 2/2, cy 1

i 21 = -----=     

8^ 2 1 21 - 1 2 /2 (X 2¹ 2^{/2 -} У )

Cxi

12 с с (а + .    °

16пх h пХ

,

A

X

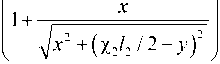
+         c y 21 ■ ¹ 21

( X 2 1 2 /2 - У + X 1 1 1 )

(                             A

¹             i                     x

1 +

^{( X} 2 ¹ 2^{2 +} X ¹ 1 ^- У ) ( x_X² + ( X 1 1 1 + X 2 1 2 /2 - y ) ² J

+        c y 21 " ¹ 21

3 % 2 ¹ 2 ^{12 +} X 1 ¹ 1 ^- У

Тогда выражения для определения коэффициента подъемной силы и индуктивного сопротивления имеют вид

C y = C y “( «- U 5 1 + 2 С ^( а- i 21 ) 5 2 , C xi = C xi 1 5 1 + 2 C xi 2 5 2 =

⁽ c “⁽a^- i 12 ) ^{) 2          (} c y “ ⁽ «^- i 21 ) )

--5 1 + 2----------------- 5 2 .

пХ1                 пХ2

Данные зависимости позволяют заменить сложное составное крыло прямоугольным крылом, эквивалентным в аэродинамическом смысле, и производить оценку аэродинамических характеристик для всего аппарата с несущей поверхностью прямоугольной формы в плане. Аэродинамические характеристики эквивалентной несущей поверхности можно оценить по формуле

C ²

L су = cy z a, Cxi= —, пХ где

C y “z = с а 1 (1 - i n) 5 1 + 2 c_y “₂(1 - i ^) 5 2 ,

C V у £

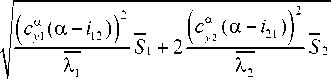
dy .

где

L /2

4= I

- L /2

X 1 /2 + у

X 1 /2 - у      .

=+ ^л ; = dy , h² V( X 1 /2 - У ) ² + 4 h² = с а^.

с yо

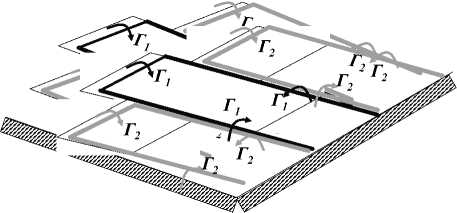
Рис. 3

Данные выражения позволяют в первом приближении оценить коэффициенты подъемной силы, индуктивного сопротивления. Однако распределение циркуляции по размаху несущей поверхности не постоянно, как было принято выше, а имеет параболический характер при движении крыла вблизи экрана [1; 2]. Поэтому для получения более адекватной модели аэродинамических характеристик необходимо заменить несущую поверхность ТАП тонкой поверхностью (это равносильно, поскольку относительная толщина несущей поверхности платформы не превышает с = 6 %) и решить нелинейную задачу ее обтекания идеальной жидкостью.

Для этого тонкую несущую поверхность заменили вихревой пеленой, для которой, выполняя условия непротекания, получили сингулярное интегральное уравнение:

Получение функциональных зависимостей определения коэффициента подъемной силы, индуктивного сопротивления вблизи экрана для составного крыла сводилось к замене «твердой стенки» крылом, находящимся на расстоянии 2 h от первого, где h - расстояние от несущей поверхности до экрана (рис. 3). Тогда, зная зависимости для определения коэффициента подъемной силы, индуктивного сопротивления крыла прямоугольной формы в плане вблизи экрана, можно определить эти же коэффициенты для эквивалентного крыла, заменяющего составное крыло, и тем самым оценить аэродинамические характеристики ТАП с консолями.

В этом случае, с учетом влияния экрана, зависимости для определения коэффициента подъемной силы, индуктивного сопротивления примут вид

X

су = СУо (« +

с уо

16л% h

а + df = - 1 ГУМ dx    4п V„ 5 z - zo

+

1+

У ( x , z )

x - xo

^{( x -} x o ⁾² + ⁽ z ^- z o ⁾²

V ( z - Z o ) ² + 4( H + (0,5 b - x o )sin а ) ²

x - x

7 ( x - ^xo ) ² + ( z - Z o ) ² + 4( H + (0,5 b - ^xo )sin a ) ²

+

dS .

Разрешить данное сингулярное уравнение относительно циркуляции возможно, используя численные методы, в частности, панельный метод или метод дискретных вихрей, имеющий преимущества перед другими численными методами в меньшем затрате машинных ресурсов по сравнению с методом конечных элементов, методом граничных элементов, методом конечных разностей и, самое главное, учитывающий физику явления. В этом случае вихревая пе-

лена заменялась системой П-образных вихрей посто

янной циркуляции:

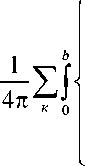
( X ^- x , )( X 2 ^- x j + ( z ^- z 1 ⁾⁽z ₂ ^- z j        +

[ ( x ^- x 1 ^{) 2} + ( z ^- z 1 ^{) 2} ]• [ ( x 2 ^- x 1 ^{) 2} + ( z 2 ^- z 1 ^{) 2} ]

+         ⁽ x ^- x 2 ⁾⁽ x 1 ^- x 2 ) + ⁽ z ^- z 2 ⁾⁽ z 1 ^- z 2 )

[ ⁽ x ^- x 2 ^{) 2} + ⁽ z ^- z 2 ^{) 2} ]• [ ⁽ x 2 ^- x 1 ^{) 2} + ⁽ z 2 ^- z 1 ^{) 2} ]

[ ( z ₂ - z ) x + z x ₂ - z ₂ x 1 - z ( x ₂ - x ₁) ] ( x ₂ - x ₁ ) у ( x ) dx +

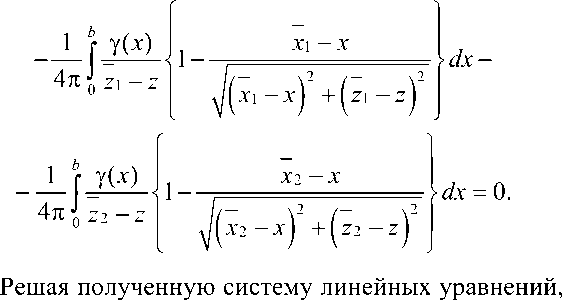
+Xfj(x)_, 4nf z1- z

-

-

• 1

) ^{2 +( z} 1 ^{- z} ) ²

> dx +

b

+-1- f

4 n * z ₂ - z

Y ⁽ x )

-

-

' 2

^{) 2 +(} z - 2

z)2 J

> dx

-

( x - x 1 )( x 2 - x 1 ) + ( z

-

z 1 )( z 2 - z 1 )

1 ъ

- -1 EH

4*Kf

z - z 1

( x - x 2 )( x 1

-

z

:2 - x 1 ) ² + ( z 2 - z 1

x 2 ) + ( z - z 2 )( z 1 - z 2 )

;

z 2

z 1 ) x + z 1 x 2

определялась величина циркуляции, по значению которой, используя теорему Жуковского «в малом», вычисляли аэродинамические характеристики: коэффициент подъемной силы, продольного момента, безразмерную величину аэродинамического давления.

Проведена серия численных экспериментов, включающих моделирование составного крыла без шайб на центроплане и с шайбами высотой h = 0,05, результатом которых явилось следующее: графическое представление распределения коэффициента давления по поверхности аппарата (рис. 4), числовые значения коэффициента подъемной силы, продольного момента, безразмерной координаты аэродинамического фокуса (рис. 5).

z 2 x 1

z ( x 2 - x 1 ) J ( x 2 - x 1 ) y ( x ) dx

Рис. 4: а - составное крыло с шайбами; б - составное крыло без шайб

б

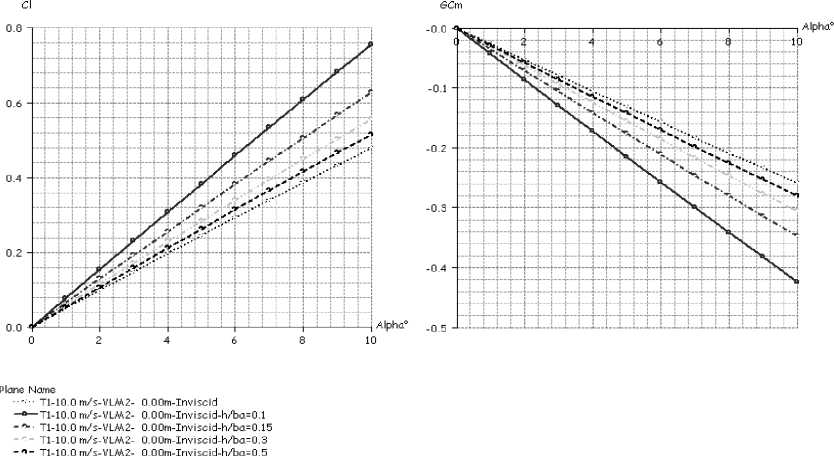
Рис. 5

На основе полученных числовых значений аэродинамических коэффициентов сделаны следующие выводы:

– перемещение консолей вдоль центроплана к хвостовой части приводит к увеличению продольного пикирующего момента и, как следствие, увеличению координат фокусов, при этом зависимость момента от положения консолей, как и фокусов, имеет линейный вид, однако при приближении к хвостовой части продольный момент имеет параболическую зависимость от координаты положения консолей (рис. 6, 7);

– максимальная несущая способность платформы без шайб реализуется при центральном расположении консолей, при этом зависимость между положением консолей и коэффициентом подъемной силы имеет параболический характер, и выражен он тем сильнее, чем меньше отстояние от экрана и больше уг о л атаки (рис. 7);

- установка шайб высотой h = 0,05 на центроплан приводит к некоторому уменьшению несущей способности всей системы, это связано с отрицательным взаимным влиянием шайб и консолей крыла (рис. 6, а ); уменьшить отрицательное влияние можно придав консолям положительный угол поперечного V или вынеся их выше центроплана, как это сделано на проекте экраноплана ЭП-200 (ЗАО «АТТ–АТТК»);

– максимальное значение коэффициента подъемной силы достигается при более переднем расположении консолей по сравнению с вариантом без шайб, при этом график зависимости коэффициента подъемной силы от положения консолей имеет меньшую величину кривизны по сравнению с тем же графиком для составного крыла без шайб, что говорит об уменьшении влияния положения консолей на аэродинамические характеристики платформы с установленными шайбами (рис. 7);

– наличие шайб приводит к увеличению безразмерных координат фокусов (смещению к хвостовой кромке) и меньшей чувствительности от величины отстояния от экрана, что обеспечит установку для балансировки меньшей площади оперения, а следовательно, более высокую транспортную эффективность.

Используя числовые значения аэродинамических характеристик, полученных в ходе численного экспе-

римента, на основе метода наименьших квадратов получены функциональные зависимости для определения значений аэродинамических коэффициентов составного крыла:

– подъемной силы:

—          —         —     X ⁰'227 S ^о,00⁵ x ^0,14

с у ^(а , h ' x ) = ⁽ с уао ц S ¹ + c yao к S ² )    0'21 , 0'042- 0,42 <-,0,012 ^;

ex    h    X 1   s 2

– продольного момента:

mz ( а, h' x) = (mz S1 + m   S2 - cya цк

h 0,075 S 0,205

x ) a ⁰'⁷⁶ X ⁶ ₂ '⁵¹X0'⁷¹ S 1⁰'³⁸ ;

– индуктивного сопротивления:

при

с xi

nX

(1 + A)-

[ C y ( a ' h ' x

8nX k

. 2 )

= +

X

x In

1 - k + 74 h ² ■ cos ² ( a ) + ( k - 1) ²

-

,

этом среднеквадратичное отклонение получае-

мых результатов составляет не более 0,05.

Таким образом, на основе числовых результатов численных экспериментов получены функциональные зависимости, позволяющие оценить аэродинамические характеристики проектируемых ТАП компоновки «составное крыло», а также сделать следующий вывод: при проектировании новых ТАП данной компоновки с целью увеличения мореходности при волнении оптимальным будет центральное размещение консолей с установленными на центроплане шайбами.