Влияние поперечной нагрузки на устойчивость сжимаемого продольной силой стержня

Исследование задач устойчивости гибких элементов конструкций и упругих систем в настоящее время занимает одно из центральных мест в механике деформируемого твердого тела и представляет значительный интерес. Теория устойчивости упругих систем берет свое начало с работ Эйлера по теории продольного изгиба [1]. Проблемы упругой устойчивости исследовались многими авторами [2–5]. Вариационный подход к данным задачам был развит С.П. Тимошенко [6], который решил ряд задач устойчивости стержней, пластин и оболочек. На основе вариационного подхода можно доказать теорему существования решения уравнений равновесия. Также можно убедиться, что в устойчивом положении равновесия функционал полной энергии достигает локального минимума. Общая концепция упругой бифуркационной устойчивости предложена в монографии В.В. Новожилова [7]. В связи со стремительным развитием вычислительной техники и появлением универсальных численных алгоритмов решения краевых задач (метод граничных элементов, метод конечных элементов), к настоящему времени имеются комплексы программ, позволяющие рассчитывать упругие конструкции на устойчивость, например [3].

В общем случае проблемы упругой устойчивости сводятся к нахождению точек бифуркации некоторых нелинейных уравнений, или к нахождению параметров, при которых некоторая вариационная задача имеет несколько решений.

Предположим, что полная потенциальная энергия упругой конструкции имеет вид

Ф( u, X ) = F ( u ) + G ( u,X ) , (1)

где u – функция, характеризующая состояние упругой системы (это может быть, например, вектор перемещения, тензор деформации и т.д.), F ( u ) - упругая энергия системы, G(u, X ) - работа внешних сил, X - параметр, характеризующий внешнюю нагрузку. Пусть уравнение Эйлера для функционала (1) записывается в виде

L ( u,X ) = 0 , (2)

где L – дифференциальный, вообще говоря, нелинейный оператор. Поиск критического параметра λ сводится к нахождению точек бифуркации уравнения (2) .

Одной из важных проблем является задача изучения влияния односторонних связей на устойчивость упругой конструкции. Наличие таких связей приводит к появлению неравенств, которым должны удовлетворять перемещения.

Интересные задачи устойчивости упругих систем при односторонних ограничениях на перемещения решены В.И. Феодосьевым [4]. Он рассмотрел задачу плоского изгиба упругого стержня, находящегося в первоначальном недеформированном состоянии между двумя жесткими стенками на одинаковом расстоянии от каждой из них, исследована задача устойчивости тонкостенного кольца, сжимаемого накинутой на него абсолютно гибкой нерастя- жимой нитью, натягиваемой силой, а также кольца, вставленного в жесткую обойму. Влияние односторонних связей на устойчивость цилиндрических оболочек при осевом сжатии изучалось в работе [8]. Анализ упругих систем на устойчивость при наличии односторонних (неудерживающих) связей сводится к определению параметров, при которых задача оптимизации имеет не единственное решение. Это, в свою очередь, приводит к необходимости решать невыпуклые задачи математического программирования с применением методов глобальной оптимизации. Общая теория и методы решения задач устойчивости упругих систем при наличии односторонних связей изложены в работе [9]. Во многих случаях системы, ограниченные односторонними связями, сводятся к идентификации условной положительности квадратичных форм на конусах. Алгебраический критерий условной положительности в самом важном случае, когда конус есть неотрицательный ортант в Rn, предложен в работах В.Л. Крепса [10] и Л.Б. Рапопорта [11]. Систематическому применению неравенств в механике посвящена монография П. Панагиотопу-лоса [12].

Некоторые контактные задачи, в том числе и задачи устойчивости упругих систем при наличии односторонних ограничений на перемещения, и методы их решений рассмотрены в трудах [13], [14].

В данной работе показано влияние поперечной нагрузки на устойчивость сжимаемого продольной силой стержня. Предполается, что прогибы стержня с одной стороны ограничены жестким препятствием.

Гибкий стержень, нагруженный продольной сжимающей силой и поперечной нагрузкой

l и (i; w ) = / EJ^2-2-p (1 -cos

Ф )+ qw ds ^ min , w,φ

где E — модуль Юнга, J — момент инерции поперечного сечения стержня, l — длина стержня. При этом выполняются геометрические равенства

w ’ _s = sin ф,   z ‘ _s = cos ф.            (4)

Предположим, что сила P больше первой критической силы Эйлера и выполнено неравенство 4 п ² EJ/l ² < P <  16 п ² EJ/l ² . Пусть ( l 1 ,l ₂ ) — интервал максимальной длины, на котором w ( s ) >  0 . Ясно, что ф ( l 1 ) = ф ( l ₂ ) = 0 , w ( l 1 ) = w ( l ₂ ) = 0 , поэтому можно считать, что l 1 = 0 , l ₂ > l/ 2 и w ( s ) = 0 , s Е [0 , l ₂ ] . Определение перемещений на интервале [0 ,l ₂ ] сводится к задаче изопериметрического типа

U ( w, l ₂ ) ^ min , w,φ,l 2

l 2

j sin фds = 0

при условиях (3), (4).

Составим по обычным правилам вариационного исчисления функционал Лагранжа

L ( w,ф,l 2 ) = U ( w,l 2 ) +

l 2

+ J ( A ( w S

— sin ф ) + m 1 sin ф ) ds.

Система уравнений Эйлера для функционала L ( w,ф,l ₂ ) имеет вид

Рассмотрим стержень длины l, нагруженный продольной сжимающей силой P и поперечной силой q >  0 . Пусть w = w ( s ) , z = z ( s ) — координаты точек упругой линии, s — длина дуги, w ( s ) — прогиб, ось z совпадает с первоначальной недеформированной осью стержня (рис. 1).

EJф'_{a s} + P sin ф — m 1 cos ф + A cos ф = 0 ,

A ’ = q.                       (7)

Из второго уравнения получаем A = — qs + m ₂ . Сделаем замену переменных s = l ₂ т и введем обозначения

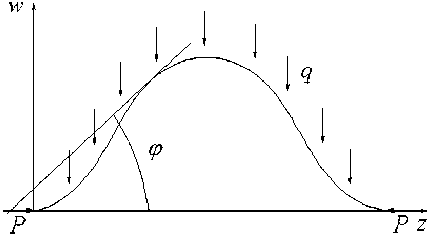
Рисунок 1. Направление действующих сил и форма прогиба стержня.

Figure 1. The direction of the acting forces and the shape of the deflection of the rod.

Предположим, что прогиб стержня ограничен с одной стороны жестким препятствием, так что w ( s ) >  0 . Обозначим через φ угол между касательной к упругой линии и осью z. Для определенности предположим, что выполнены граничные условия жесткой заделки

k ²

Pl 2

EJ ,

= ql 3

p EJ'

m =

( m i — m 2 ) l ²    1

EJ    ⁺ 2 ^P"

Первое из уравнений (7) записывается в виде

_φ ′′

—k ² sin ф — p ( т —

cos ф + m cos ф,

Ф = 0 , w = 0 при s = 0 ,l.         (3)

Определение упругой линии стержня сводится к следующей вариационной проблеме

где штрих обозначает производную по τ . Из условия минимума функционала (6) по переменной l 2 (если l 2 < l ) получаем еще одно граничное условие ф (1) = 0 . Уравнение (9) не интегрируется в квадратурах.

Умножая обе части уравнения (9) на ф ( т ) и интегрируя в пределах от 0 до 1, получим ф ² (1) = ф ² (0) . Ясно, что ф (0) >  0 и ф (1) >  0 , ибо в противном случае в достаточно малой окрестности концов интервала [0 , 1] прогиб будет принимать отрицательные значения. Но тогда ф (0) = ф (1) . Из последнего равенства следует, что функция w ( т ) симметрична относительно середины интервала [0 , 1] , т.е. для т Е [0 , 2 ]

w (2 ^—т )= w (2+ ^т ) , ф (2 ^—т )= ^— ф (2+ ^т ) •

Интегрируя уравнение (7) в пределах от 0 до1, получим, что 1

m J cos фdт = 0 , а значит, и m = 0 .

Граничные условия жесткой заделки

Пусть ф(а; т) — решение уравнения (9) при m = 0 c начальными условиями ф(0) = 0, ф'(0) = а (решение τ задачи Коши) и w(а; т) = / sin(ф(а; t))dt. Обозначим 0

ш ( а ) = ф ( а ; 1) , ф ( а ) = w ( а ; 1) , тогда

£ ( а ) = V w 2 ( а ) + ш ² ( а ) .

При фиксированных значениях k и ρ находим все значения параметра α, при которых

С ( а ) = 0 ,                       (10)

т.е. одновременно ^ ( а ) = 0 и ш ( а ) = 0 . Если w ( а ; т ) >  0 для всех значений т Е [0 , 1] , то при заданных к и р найдено допустимое положение равновесия.

Графики функции £ ( а ) представлены на рис. 2 и 3. Результаты вычислений для к = 2 . 05 п приведены в табл. 1.

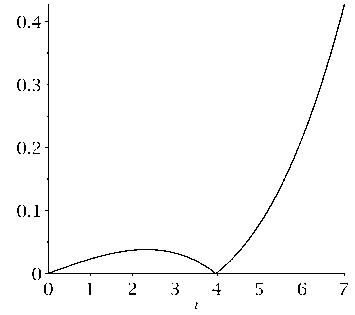
Рисунок 2. График функции ξ ( α ) при k = 2 . 05 π, q = 0 для граничных условий жесткой заделки.

Figure 2. Graph of the function ξ ( α ) for k = 2 . 05 π, q = 0 for boundary conditions of rigid termination.

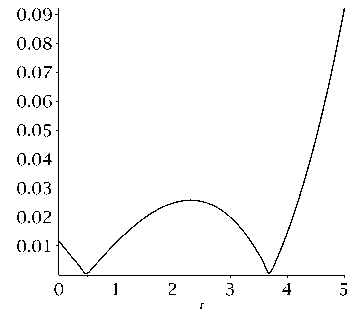
Рисунок 3. График функции ξ ( α ) при k = 2 . 05 π, q = 0 . 5 для граничных условий жесткой заделки.

Figure 3. Graph of the function ξ ( α ) for k = 2 . 05 π, q = 0 . 5 for boundary conditions of rigid termination.

Таблица 1

Результаты вычислений при k = 2 . 05 π , граничные условия жесткой заделки

Table 1

Calculation results for k = 2 . 05 π , boundary conditions of rigid termination

ρ	0	0 . 5	1	1 . 3	р* = 1 . 6
α 1	0	0 . 471	0 . 414	1 . 414	2 . 26
U 1	0	- 0 . 05	- 0 . 268	- 0 . 499	- 1 . 27
w max	0	0 . 025	0 . 054	0 . 1285	0 . 115
α 2	3 . 958	3 . 02	6 . 55	6 . 4	2 . 26
U 2	- 3 . 868	- 2 . 693	- 2 . 69	- 2 . 256	- 1 . 274
w max	0 . 1909	0 . 179	0 . 163	0 . 151	0 . 115

При р = 0 существуют два корня уравнения (10): первый корень а 1 = 0 соответствует тривиальному решению ф(т) = 0, w(т) = 0, т Е [0, 1], второй корень дает нетривиальное положение равновесия стержня. При при увеличении ρ появляется два нетривиальных решения уравнения (10) (рис. 3).

При ρ > ρ∗ у уравнения (10) нет решений. При мень- ших значениях ρ имеются два корня α1 и α2, α1 < α2, (а2 — а 1) ^ 0 при р ^ р*. Первый корень а 1 возрастает, второй корень а2 убывает, а при р = р* они сливаются в один. В табл. 1 приведены U1 и U2 — значения интеграла U(w) = J фр'2 — к2 (1 — cos ф) — рw^dт. Этот интеграл с точностью до положительной константы совпадает с полной энергией системы. U1 соответствует корню α1, а U2 — корню α2.

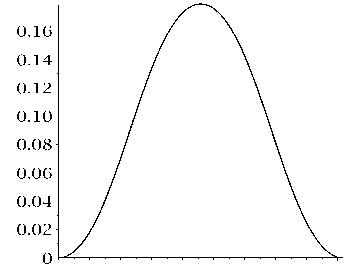
На рис. 4 представлена упругая кривая при граничных условиях жесткой заделки. На этом и последующих рисунках по оси абсцисс отложена координата z ( т ) , а по оси ординат — координата w ( т ) .

О 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

Рисунок 4. Упругая кривая {z ( т ); w ( т ) }, т Е [0 , 1] , к = 2 . 05 п, ρ = 0 . 5 для граничных условий жесткой заделки.

Figure 4. Elastic curve {z ( т ); w ( т ) }, т Е [0 , 1] , к = 2 . 05 п , р = 0 . 5 , for boundary conditions of rigid termination.

Граничные условия шарнирного опирания

Эти условия означают, что на концах стержня отсутствуют перемещения и изгибающие моменты равны нулю, т.е.

w (0) = 0 , w " (0) = 0 , w (1) = 0 , w '' (1) = 0 .    (11)

Из (4) следует, что (11) эквивалентно условиям ф'(s) = 0, w(s) = 0 при s = 0,l.

На рис. 5 представлена упругая кривая при к = 1 . 3 п, q = 0 .

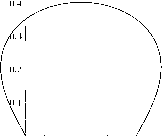
0.05 0   0.05 0.10 0.15 0.20 0.25

Рисунок 5. Упругая кривая {z ( т ); w ( т ) }, т Е [0 , 1] , к = 1 . 3 п, ρ = 0 для граничных условий шарнирного опирания.

Figure 5. Elastic curve {z ( т ); w ( т ) }, т Е [0 , 1] , к = 1 . 3 п, р = 0 for boundary conditions of the hinge support.

При данных значениях параметров ( к = 1 . 3 п, q = 0) существует единственная кривая, которая является формой равновесия. Как и в случае граничных условий жесткой заделки при q >  0 , обозначим w ( а ) = ф ( а ; 1) , ^ ( а ) = w ( а ; 1) , £ ( а ) = ^ w ² ( а) + w ² ( а ) . Далее находим все значения параметра а , при которых £ ( а) = 0 , т.е.

w (0) = 0 , w ‘ (0) = 0 , w (1) = 0 , w ‘ (1) = 0 .   (12)

Результаты вычислений при к = 1 . 3 п приведены в табл. 2.

Таблица 2

Результаты вычислений при k = 1 . 3 π для граничных условий шарнирного опирания

Table 2

Calculation results for k = 1 . 3 π for boundary conditions of the hinge support

ρ	0	20	30	30 . 45	40
α 1	0	1 . 05	1 . 38	1 . 38	1 . 55
U 1	0	- 0 . 381	- 0 . 116	0 . 0089	1 . 05
w max	0	0 . 297	0 . 353	0 . 373	0 . 358
α 2	1 . 93	2 . 12	2 . 30	2 . 325	2 . 56
U 2	- 11 . 9	- 8 . 79	- 8 . 39	- 8 . 45	- 9 . 07
w max	0 . 403	0 . 396	0 . 38	0 . 373	0 . 358

Как и в случае жесткой заделки при q >  0 (не очень больших), найдется два решения уравнения (12) α 1 и α 2 , графики которых представлены на рис. 6 и 7 при к = 1 . 3 п, р = 30 .

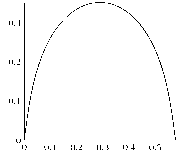
Рисунок 6. Упругая кривая {z ( т ); w ( т ) }, т Е [0 , 1] , к = 1 . 3 п, q = 30 , α 1 = 1 . 38 для граничных условий шарнирного опирания.

Figure 6. Elastic curve {z ( т ); w ( т ) }, т Е [0 , 1] , к = 1 . 3 п, q = 30 , α 1 = 1 . 38 for boundary conditions of the hinge support.

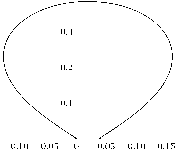
Рисунок 7. Упругая кривая {z ( т ); w ( т ) }, т Е [0 , 1] , к = 1 . 3 п, q = 30 , α 2 = 2 . 30 для граничных условий шарнирного опирания.

Figure 7. Elastic curve {z ( т ); w ( т ) }, т Е [0 , 1] , к = 1 . 3 п, q = 30 , α 2 = 2 . 30 for boundary conditions of the hinge support.

Таблица 3

Результаты вычислений при k = 1 . 1 π для граничных условий шарнирного опирания

Table 3

Calculation results for k = 1 . 1 π for boundary conditions of the hinge support

ρ	0	2	2 . 5	3 . 0	4 . 0
α 1	0	0 . 408	. 5495	-	-
U 1	0	- 0 . 291	- 0 . 546	-	-
w max	0	0 . 128	0 . 549	-	-
α 2	1 . 21	1 . 07	0 . 801	0 . 801	0 . 801
U 2	- 3 . 67	- 2 . 55	- 2 . 09	- 1 . 24	- 1 . 15
w max	0 . 329	0 . 301	0 . 284	0 . 23	0 . 241

Результаты вычислений существенно зависят от величины продольной силы k. Для небольших значений k при увеличении поперечной нагрузки q первый корень α 1 исчезает (табл. 3). В частности, при к = 1 . 1 п, q >  3 остается только один корень уравнения (12). Если k достаточно велико, то начиная с некоторых q первому корню будет соответствовать положительное значение полной энергии. Например, при к = 1 . 3 п , р >  301 . 45 , что говорит о неусточивости такого положения равновесия. Поэтому на практике оно не реализуется.