Влияние потерь на оптические свойства хиральной метамембраны

Явления, возникающие при взаимодействии электромагнитных волн с хиральными системами и приводящие к возникновению циркулярного дихроизма отражения, пропускания и поглощения, широко известны и находят ряд применений в различных областях [1 –6], в том числе и таких важных, как медицинская промышленность [7]. Подобные явления возникают, например, в хиральных метаматериалах и метаповерхностях, которые при небольших (субволновых) толщинах позволяют контролировать и преобразовывать электромагнитные волны в широких пределах [8– 11]. До появления хиральных метамембран основным способом управления дихроичными свойствами света было использование холестириче-ских жидких кристаллов, см. в работах [12, 13]. Интересный способ создания циркулярного дихроизма, основанный на включении оптически активного слоя в кольцевой резонатор, был предложен в работе [14].

Хиральные метаповерхности обладают широким многообразием оптических свойств [15]. В последнее время особый интерес вызывают метаповерхности с так называемой максимальной хиральностью, например, полностью пропускающие излучение одного знака циркулярной поляризации со сменой знака циркулярной поляризации и отражающие излучение другого знака циркулярной поляризации без конверсии [16–27].

Один из подходов, применяемых при разработке метаповерхностей для взаимодействия с циркулярно поляризованным светом, связан с изготовлением плазмонных структур [28–31]. Однако недостатком подобных структур является наличие значительных потерь на поглощение и связанной с ними низкой эффективностью интенсивности оптических преобразований [24, 32, 33]. Выходом является использование прозрачных диэлектрических систем, которые позволяют достичь требуемого результата при отсутствии потерь [17, 25].

Однако даже при изготовлении образцов из прозрачных диэлектриков возникают потери, связанные, например, с рассеянием на дефектах реально изготовляемой структуры. Этим можно объяснить уширение резонансов и уменьшение пиковых значений характерных величин, например, коэффициентов отражения или пропускания в заданной поляризации или степени циркулярной поляризации отражения или пропускания в экспериментах по сравнению с теоретическими расчётами [18, 27]. Кроме того, в некоторых случаях изготовление метаповерхности может сопровождаться модификацией ее приповерхностных слоев, например, металлизацией, как это происходит вследствие графитизации поверхности при лазерной абляции алмаза [34].

В данной работе теоретически исследовано влияние поверхностных дефектов изготовления или металлизации на оптические спектры хиральной метаповерхности из прозрачного диэлектрика с номинально максимальной хиральностью отражения и пропускания. Наличие приповерхностных рассеива- ющих дефектов или металлизации моделировалось увеличением мнимой части показателя преломления тонких приповерхностных слоев метаповерхности. В качестве примера рассмотрена хиральная метаповерхность (метамембрана) из алмаза для диапазона длин волн λ = 10 – 12 мкм (частоты 830-1000 см –1). Этот диапазон длин волн входит в окно прозрачности атмосферы, в нем активно ведутся разработки мощных лазерных источников, для управления излучением которых требуется создание новой радиационно-стойкой оптики. Подходящим кандидатом для этой цели является алмаз, обладающий прозрачностью, химической инертностью и рекордной теплопроводностью.

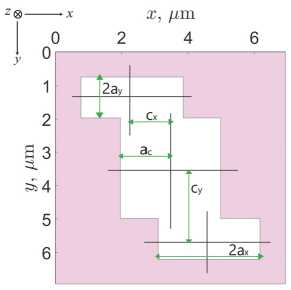
В работе исследуется метамембрана в виде квадратной решетки с элементарной ячейкой, показанной на рис. 1, в подписи к которому приведены все ее размеры. Поскольку период решетки порядка 7 мкм меньше длины волны света в интересующем нас диапазоне 10– 12 мкм, все дифракционные каналы закрыты и мембрана ведет себя как однородный слой с хиральным откликом, то есть является хиральной метамембраной.

а)

б)

в)

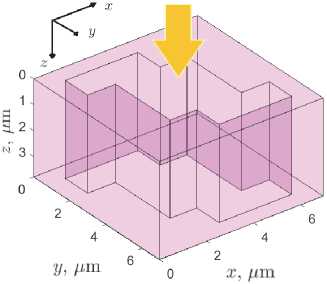
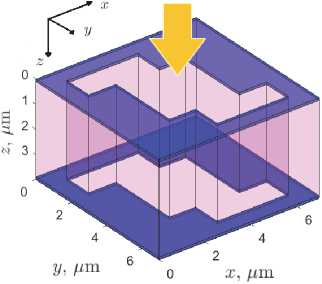
Рис. 1. Схематическое изображение элементарной ячейки хиральной метамембраны, представляющей собой квадратную ячейку в плоскости xy . Размеры ячейки оптимизированы для алмаза с диэлектрической проницаемостью εD = 5,76 (показан фиолетовым цветом) и достижения максимальной хиральности на длине волны 11 мкм и равны px=py×h, px×py = 6,95 мкм, h = 4 мкм (здесь и ниже все размеры даны в микронах, если специально не указана размерность). (a) Вид сверху. Размер центрального квадрата 2ac×2ac, ac = 1,51. Центры боковых прямоугольников смещены в точки с координатами (±cx×±cy), cx = 1,16, cy = 2,12 и их размеры (2ax×2ay), ax = 1,54, ay = 0,62. (б-в) Вид сбоку. В панели (в) сверху и снизу добавлены для описания потерь на рассеяние и/или поглощающие слои (выделены синим цветом) толщины hA = 100 нм и с комплексной диэлектрической проницаемостью εA = εA' + iεA''. Плоская электромагнитная волна падает на структуру по нормали к ней (оранжевые стрелки на панелях (б) и (в))

Что касается выбора геометрии ячейки, мы стартовали с геометрии хиральной метамембраны, предложенной в работе [16], но из другого материала (SiN) и для длины волны в ближнем ИК-диапазоне 870 нм. Элементарная ячейка предложенной в [16] метамембраны содержит три отверстия – цилиндрическое в центре ячейки и два эллиптической формы по бокам. Поскольку, однако, мы ориентировались на другую возможную технологию изготовления метамембраны, метод лазерной абляции, представлялось разумным объединить эти три отверстия в одно, но более сложной формы (что позволяет в три раза уменьшить число лазерных импульсов на ячейку). При реальном изготовлении такой метамембраны, конечно, отверстия неизбежно будут с закругленными краями. Однако учет такой закругленности привел бы к существенному замедлению численного счета с использованием адаптивного пространственного разрешения [37–39]. Замена закругленных отверстий прямоугольными не приводит, как показывают наши расчеты, к качественному изменению оптического отклика в случае диэлектрических материалов метамембраны.

Для расчета спектров коэффициентов пропускания, отражения и поглощения в исследуемых слоистых пространственно-модулированных структурах было использовано фурье-модальное разложение и метод оптической матрицы рассеяния [35], реализованные в пакете Матлаб c применением так называемых правил факторизации Ли (Li’s factorization rules, [36]), а также адаптивного пространственного разрешения Гране (Granet’s adaptive spatial resolution, [37– 39]). Метод состоит в разделении структуры на однородные в перпендикулярном направлении слои (например, для структуры на рис. 1б воздух, фотонный кристалл с вертикальными стенками, воздух), решении в этих слоях уравнений Максвелла в базисе плоских волн на обратной решетке фотонного кристалла и сшивке решений в соседних слоях в соответствии с граничными условиями для уравнений Максвелла. И факторизация Ли, и адаптивное пространственное разрешение Гране позволяют уменьшить влияние эффекта Гиббса, приводящего к неточностям разложений в конечном фурье-базисе. Например, адаптивное пространственное разрешение предполагает фурье-модальное разложение в пространстве, неоднородно растянутом вокруг границ метаматериала с резким изменением диэлектрической проницаемости. Во всех приведенных ниже расчетах циркулярно-поляризованная монохроматическая электромагнитная волна падает по нормали к поверхности.

В базисе круговых поляризаций оптические коэффициенты делятся на описывающие отражение и пропускание без конверсии направления вращения поля в пространстве (безотносительно к направлению распространения волны) и с конверсией. Последние отсутствуют в структурах с вращательной осью симметрии C n , n ≥ 3 [21], однако в нашем случае n =2, конверсия, вообще говоря, имеется и циркулярный дихроизм пропускания и отражения возникает даже при отсутствии потерь.

Исследование

Обозначим коэффициенты отражения по интенсивности из лево-циркулярно поляризованного состояния (LCP – от англ. Left Circular Polarization) в право-циркулярно поляризованное (RCP) Rrl и наоборот, из RCP в LCP – Rlr. Аналогично для коэффициентов пропускания из LCP в LCP – Tll и из RCP в RCP – Trr. Такие процессы рассеяния не сопровождаются сменой направления вращения в пространстве. Мы используем стандартные для оптики обозначения компонент циркулярно поляризованного света, которые привязаны не к абсолютному положению в пространстве, а к направлению распространения волны. Поэтому, например, при отражении с сохранением направления вращения поля в пространстве в обсуждении выше правая циркулярная поляризация пере- ходит в левую и наоборот. Аналогично обозначены и коэффициенты со сменой направления вращения: для отражения (пропускания) из LCP в LCP (RCP) – Rll (Trl) и т.д. Оптические коэффициенты по интенсивности являются положительными числами, поскольку связаны с соответствующими комплексными амплитудными коэффициентами соотношениями

R_u =| r «l2, T i^ ■■■.                           (1)

Вследствие симметрии по отношению к обращению во времени (см., например, в [21]) амплитудные коэффициенты без смены направления вращения равны rlr =rrl,trr =tll.                                                    (2)

Поэтому в соответствии с (1)

R_lr = R_rl , T_rr = T_ll .                                      (3)

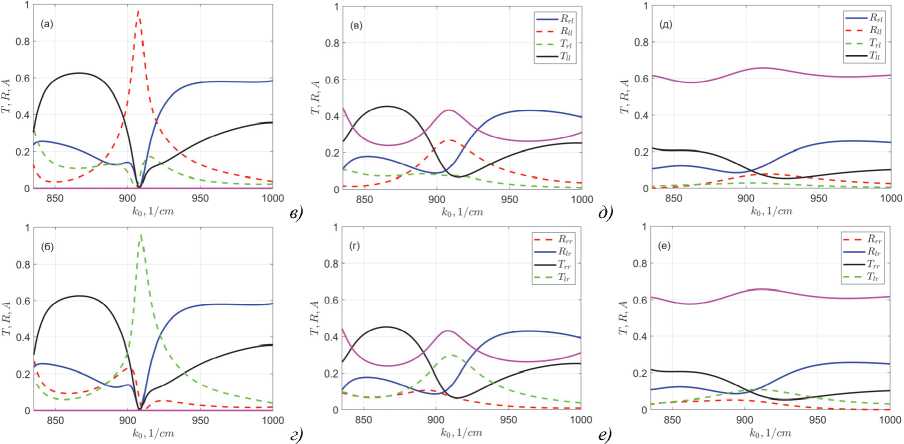
“Расчетные оптические спектры описанной выше метамембраны в случае отсутствия потерь показаны на панелях а ) и б ) рис. 2, для падающей LCP- и RCP-волны, соответственно. Сплошными линиями показаны процессы без смены направления вращения (вследствие соотношения (3) они одинаковы в панелях а ) и б ), а штриховыми – со сменой направления вращения”.

a)

б)

Pис. 2. Спектры отражения, пропускания и поглощения структуры в базисе круговых поляризаций для левой (панели (a, в, д)) и правой (панели (б, г, е)) круговых поляризаций входного излучения. Спектры потерь в соответствующих круговых поляризациях показаны фиолетовыми сплошными линиями на всех панелях. Панели ((a, б)), ((в, г)) и ((д, е)) рассчитаны соответственно для ε A' = ε D и ε A'' = 0,5 и 20. Волновое число k 0 = 1 / λ

Узкий резонанс вблизи длины волны 11 мкм как раз и демонстрирует максимально возможный циркулярный дихроизм отражения и пропускания (максимально возможную хиральность) оптимизированной метамембраны: падающий на структуру право поляризованный свет с длиной волны вблизи 11 мкм практически полностью проходит через метамембрану с конверсией в лево поляризованный, а лево поляризованный практически полностью отражается в лево поляризованный свет, как видно из рис. 1а, б. Приведенные выше геометрические параметры хиральной структуры были численно оптимизированы нами методом градиентного спуска именно для получения оптического отклика с максимальной хиральностью.

На рис . 3 показаны практически достигающие предельных значений ± 1 спектры степени циркулярного дихроизма отражения и пропускания , определенные как

T-T

CDR = ^RlRr , CDT = ^TlTr ,                 (4)

Rl+Rr         Tl+Tr где Rl = Rrl + Rll и т.д.

Насколько нам известно, впервые максимально хиральные метаповерхности с геометрией такого типа были представлены в работе [16] для метаматериала на основе нитрида кремния и для длины волны в оптическом диапазоне. На рис. 2в – е показаны рассчитанные оптические спектры метамембраны при включении в нее поглощающих слоев толщины 100 нм (с сохранением полной толщины мембраны), как показано на рис . 1в, и с диэлектрической проницаемостью εA'= εD и εA''=5 (панели в, г) и 20 (панели д, е).

Фиолетовые линии на всех панелях рис. 2 показывают спектр коэффициента поглощения структуры в соответствующих циркулярных поляризациях

A l =1 - R l - T l , A r =1 - R r - T r . (5)

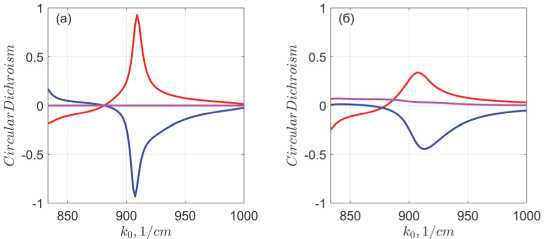
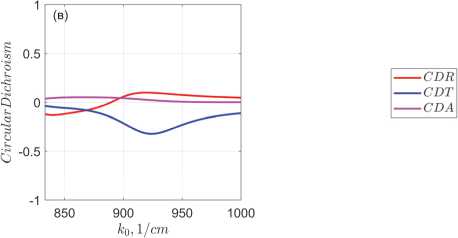
Pис. 3. Степень циркулярного дихроизма отражения, пропускания и поглощения. Панели (а), (б) и (в) рассчитаны соответственно для ε A' = ε D и ε A'' = 0,5 и 20, как и на рис. 2

Видно, что хиральность оптических свойств метамембраны, в пределе полного отсутствия потерь обладающей максимальной хиральностью, быстро деградирует с добавлением потерь, и в случае большой величины последних практически исчезает. Физическая причина этого очевидна и связана с резонансным нарастанием поглощения на частоте резонанса. Это хорошо видно по эволюции спектров поглощения на рис. 2, а также по поведению с нарастанием поглощения спектра циркулярного дихроизма нашей метамембраны, показанному на рис. 3 б и возникающему, из-за этого ослабления оптических переходов со сменой циркулярной поляризации.

Из рис. 3 также видно, что степень циркулярного дихроизма поглощения в рассматриваемой метамембране, определенная как

CDA =

A_l - A_r

A l + A r ^,

во всех рассмотренных случаях невелика. При отсутствии потерь она мала из-за симметрии по отношению к обращению во времени и, собственно, отсутствия поглощения, а при умеренных и больших потерях мала из-за резонансно увеличивающегося поглощения. А то, что циркулярный дихроизм пропускания остается большим в пределе сильного поглощения, обязано малости величины пропускания в этом случае.

Отметим, что значение мнимой части диэлектрической проницаемости εA'' =20 по порядку величины соответствует мнимой части диэлектрической проницаемости графитизированного алмаза в этом частотном диапазоне [34]. Графитизация обычно возникает в процессе лазерной обработки (абляции) алмаза, и это обстоятельство, в свете полученных результатов, следует иметь в виду при отработке соответствующих технологий. Добавим также, что практически во всех работах, посвященных рассматриваемым резонансам с максимальной хиральностью, экспериментальные значения степени циркулярного дихроизма, как правило, значительно отличаются от расчетных, всегда в сторону уменьшения [18, 27]. Но у этого свойства есть и возможное положительное следствие – видно, что хиральные структуры такого типа весьма чув- ствительны к чистоте поверхности, и поэтому могут быть полезными для сенсорики.

Заключение

В заключение укажем, что нами было проанализировано влияние потерь на оптические свойства диэлектрических метамембран, в случае отсутствия потерь демонстрирующих свойство максимальной хиральности оптического отклика. Показано, что с ростом потерь степень хиральности быстро уменьшается и вовсе исчезает в пределе больших потерь.

Исследования выполнены при финансовой поддержке Российского научного фонда (проект 22– 22–00961).