Влияние поверхностных эффектов в задаче теории упругости для кругового отверстия в полуплоскости
Автор: Гандилян Д.В.
Статья в выпуске: 4, 2020 года.
Бесплатный доступ
Поверхностные эффекты важны для моделирования некоторых структур, таких как нанопленки, нанопористые материалы и другие наноразмерные структуры. В данной работе рассмотрена задача теории упругости - задача о полуплоскости, содержащей круговое отверстие, растягиваемой постоянными напряжениями, приложенными на бесконечности, c учетом таких эффектов, как поверхностная упругость и поверхностные напряжения. Решение задачи получено при помощи разложения в ряды Фурье переменных, представленных в биполярной системе координат (что упрощает решение задачи, в силу того что на контуре отверстия одна из координат становится константой), а компоненты напряжений определяются через бигармоническую функцию напряжений. Коэффициенты в рядах Фурье определяются так, чтобы удовлетворить граничным условиям на контуре отверстия. Для решения задачи, помимо уравнений теории упругости, использовались уравнения поверхностной упругости, в частности, с помощью обобщенного закона Лапласа - Юнга и закона Шаттлворса вычислялось непосредственно поверхностное напряжение на контуре отверстия. Величины концентраций напряжений получены с помощью рекуррентных соотношений для компонент напряжения на границе. Полученные выражения можно рассматривать как обобщение решения задачи традиционной теории упругости. Проведены сравнения концентраций напряжений с учетом и без учета поверхностных эффектов в различных точках контура отверстия. Рассмотрено влияние, оказываемое поверхностными эффектами в зависимости концентраций напряжений от значения относительного расстояния между отверстием и границы полуплоскости. Обнаружено, что, несмотря на довольно простую геометрию в данной задаче, из-за достаточно малого расстояния между отверстием и границей полуплоскости значения концентрации напряжений с учетом и без учета поверхностного напряжения существенно отличаются друг от друга.
Поверхностная упругость, поверхностное напряжение, круговое отверстие, ряды фурье, биполярная система координат
Короткий адрес: https://sciup.org/146282021
IDR: 146282021 | УДК: 539.3 | DOI: 10.15593/perm.mech/2020.4.21
Текст научной статьи Влияние поверхностных эффектов в задаче теории упругости для кругового отверстия в полуплоскости
ВЕСТНИК ПНИПУ. МЕХАНИКА № 4, 2020PNRPU MECHANICS BULLETIN
Вблизи поверхностей твердых тел на наноуровне проявляются особые физико-механические свойства, которые могут значительно отличаться от свойств материала вдали от поверхности – начиная отличием в химических связях для приповерхностных атомов и наличия свободных радикалов и заканчивая присутствием оксидных пленок и повышенной концентрацией примесных атомов [1–3]. Один из основных способов для учета поверхностных явлений – использование, помимо уравнений теории упругости, уравнения поверхностной упругости [1–4]. Достаточно общий метод решения задач теории упругости, учитывающий поверхностные эффекты, заключающийся в использовании характерных нестандартных граничных условий, вытекающих из уравнений поверхностной упругости, был развит в работах [1–6]. Однако к настоящему времени число полученных аналитических решений ограничено, что, возможно, связано с весьма «неудобным» видом получаемых граничных условий. Значительная часть полученных решений для задач, учитывающих поверхностные эффекты, ограничено довольно простыми геометриями, такими как сферическая пора [7–9], плоскость с одиночным круговым отверстием [10], одиночная пластина [11], однако отно- сительный вклад поверхностных эффектов для круговых и сферических поверхностей минимален. В работах [12, 13] рассматривались задачи о плоскости с двумя круговыми отверстиями и в неконцентрической трубе, где влияние поверхностных эффектов было более существенным. Из недавних работ, посвященных исследованию вклада поверхностных эффектов, отметим [14–18]. В настоящей работе рассмотрена задача о круговом отверстии в подвергнутой растяжению полуплоскости; в данной задаче, несмотря на довольно простую геометрию, из-за достаточно малого расстояния между границами (т.е. между отверстием и границей полуплоскости) можно ожидать более весомого вклада поверхностных эффектов.
Отметим, что теория поверхностной упругости, используемая в настоящей работе, является наиболее распространенной, но не единственной. В данной теории, ставшей уже традиционной, в дополнение к объемным напряжениям и деформациям, предполагается существование дополнительных поверхностных напряжений, действующих подобно напряжениям в мембранах, совпадающих с внешними поверхностями тел либо внутренними поверхностями раздела. Данные поверхностные напряжения связываются с объемными деформациями посредством аналога закона Гука, а дополнительные поверхностные деформации при этом не вво- дятся. Альтернативные теории (например, [19]) рассматривают дополнительные поверхностные (интерфейсные) деформации, связываемые с объемными напряжениями. Недавно предложены также варианты теории, объединяющие данные подходы [20–22].
Отметим также, что полученные решения представляют интерес не только сами по себе, но и в качестве вспомогательных решений при решении более сложных задач, например, задач о взаимодействии пор с растущими трещинами [23–24].
1. Геометрия, биполярные координаты, общие соотношения
Рассмотрим полуплоскость, содержащую круговое отверстие и растягиваемую вдоль ее границы постоянными напряжениями, приложенными на бесконечности (рис. 1). В данной задаче выполнены условия плоской деформации, а на контуре отверстия и границе полуплоскости вводятся дополнительные соотношения, характеризующие поверхностные эффекты (см. п. 2). В случае классической упругости задача была решена в [25–27]. В настоящей работе получено обобщение данного решения с учетом поверхностных эффектов на контуре кругового отверстия и границы полуплоскости. Следуя работе [25], введем биполярную систему координат (α, β), связанную с декартовой системой координат ( х , y ) следующим образом:
же оси Ox , координатная линия a = 0 - соответствует оси Ox .
Координатные линии в = const представляют собой дуги окружностей, проходящих через точку O 1 , ортогональные окружностям a = const. Справа от оси Oy значения в > 0, а с левой стороны — в < 0, значение в = 0 соответствует оси Oy , кроме отрезка OO 1 , где координата в терпит разрыв, а именно: слева от оси Oy ( x = -0 ) в = -п , а справа ( x = +0 ) в = + п . Непосредственно в точке O 1 - a = +~ , а в не определено.
Будем считать, что известное постоянное значение a = y соответствует контуру отверстия, тогда, для радиуса отверстия R и расстояния между границей полуплоскости и центром отверстия d имеют место следующие соотношения:
R = %rnh Y, d = а coth Y, d/R = cosh Y. (3)
Компоненты тензора напряжений σ ij определяются через бигармоническую функцию напряжений Φ(α,β) следующим образом [26]:
А2Ф = 0, d4 „ d4 d4
+ 2 + d a 4 д a 2 д в 2 д в 4
- 2 X + 2 X + 1 d a 2 д в 2
d a 2
( g Ф ) = 0.
x + iy = - a coth I i
a + i в
| x + i(y + a) a + i в = ln
^ x + i (y - a)
a σ
αα
(cosh a - cos в) -^-7- sinh a—-
( Р) д в2 d a
где a e ( -^, +^ ) , в е [ -п, +п ] .
Полюс O 1 расположен на расстоянии a от полуплоскости. Масштабный коэффициент имеет вид
- sin в-- + cosh a д в
( g ф ) ,
a ° ₽₽ =
(cosh a - cos в) -^-7- sinh a—-
( P) da2 da
g = 1/
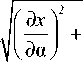
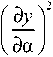
cosh a - cos в
a
- sin в-- + cos в д в
( g ф ) .
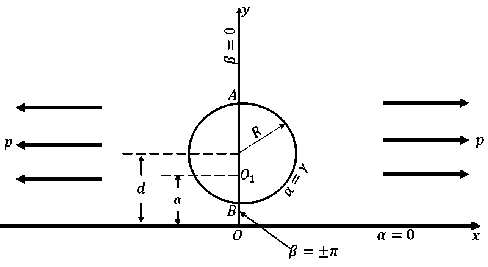
Рис. 1. Геометрия задачи
Fig. 1. The problem geometry
Координатные линии a = const представляют собой набор окружностей с центрами на оси Oy. Окружности, у которых значение α соответствуют положительным значениям, лежат выше оси Ox, а отрицательным – ни- д2
а с =в = - ( cosh a - cos в )т^"( g ф ) . д a д в
Бигармоническая функция напряжения Φ(α, β) для плоской задачи, в которой содержится круговое отверстие, представляется в виде суперпозиции двух функций [27]:
gф = g ф0 + apgF, ф0 = 2 py ,
где функция Φ0 удовлетворяет заданным напряжениям на бесконечности, а функция F подбирается так, чтобы бигармоническая функция Φ удовлетворяла известным условиям на контуре отверстия и равнялась нулю на бесконечности, т.е.
( gF ) „ =( gF ) а = в = 0 = °.
Для рассматриваемой задачи функция Φ(α, β) имеет вид [27]
g Φ ap
sinh2 α 2coshαcosβ
+ J a ( cosh a - cos в ) +
+ ( A cosh 2a + B 1 + C 1 sinh 2a ) cos в +
^
+ T f n ( a ) cos n в, n = 2
f (a) = An cosh(n + 1)a + Bn cosh(n - 1)a +
+ Cn sinh ( n +1 ) a + Dn sinh ( n -1 ) a. (7)
Для удовлетворения граничных условий на контуре отверстия (a = y) и на границе полуплоскости (a = 0) представим напряжения в виде рядов Фурье:
^
a ° aa = c 0 + E c n cos n в, n = 1
^
a °O3 = EK sin n в, (8)
n = 1
^ a C pp = d 0 + E dn cos n в, n = 1
где коэффициенты c k , b k , d k выражаются через параметры A n , B n , C n , D n J .
-
2. Постановка задачи
Задача рассматривается в постановке плоской деформации. Всюду внутри тела предполагаются выполненными основные уравнения теории упругости (уравнения равновесия, совместности и закона Гука), что автоматически обеспечивается введением бигармониче-ской функции (4).
В случае классической упругости (т.е. без учета поверхностных эффектов) граничные условия имеют вид
° aa ( a = 0 ) = ° aв ( a = 0 ) = ° aa ( a = Y ) = ° aв ( a = Y ) = 0.
Целью задачи является нахождение неизвестных коэффициентов A n , B n , C n , D n J и вычисление значения O pp на контуре отверстия. Однако если учитывать поверхностные эффекты на границах, то данные граничные условия могут не равняться нулю. Для решения задачи необходимо определить граничные условия с учетом поверхностной упругости.
В рассматриваемой теории изменения любых физических свойств, в частности упругих постоянных, с уменьшением размеров тела моделируются введением дополнительных свойств, приписываемых бесконечнотонкой поверхности, а объемные свойства предполагаются не зависящими от размера тела. Таким образом, с уменьшением размеров тела относительный вклад его поверхности возрастает, что приводит к изменению эффективных свойств с уменьшением размера.
В общем случае, с использованием обобщенного закона Лапласа – Юнга [28], граничные условия на поверхностях, редуцирующихся вследствие выполнения условий плоской деформации в линии границы полуплоскости и контура отверстия, представимы в виде о • n = -V s о', (9)
где σ – тензор объемных напряжений; n – вектор нормали к границе; σ s – тензор поверхностных напряжений; V s - поверхностный градиент [28]. Для криволинейной границы поверхностный градиент поверхностных напряжений V s о 5 представляется следующим образом:
° > + ° R 1 R 2
V , О
a 1 = a; a2 = z ; R 1 = R ; V R = 0; h = у ; h 2 = 1, (11)
° aa = R ° в ,
_ 1 cosh a - cos в д ° вв aв R sinh a дв
Аналогично для границы полуплоскости, для a = 0 параметры имеют вид a1 = a; a2 = z;
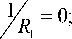
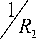
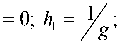
h 2 = 1, (13)
о = 0, αα ,
° . = 0. (14)
Следовательно, компоненты σαα, σαβ на границе полуплоскости не испытывают влияния поверхностных эффектов и равны нулю. Учитывая это, можно упростить выражение для бигармонической функции (7). Подставив (7) в (5) при a = 0, учитывая (14), получаем
A n + B n = ( n +1 ) C n + ( n -1 ) D n = 0, n > 1, (15)
тогда выражение для бигармонической функции можно переписать в виде gΦ ap
sinh 2 α 2coshαcosβ
+ J a ( cosh a - cos в ) +
σ
( m )
αα
= Га( m -1) _ °pp
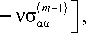
M
+ A (cosh 2a -1) cos в + £ [ An (cosh(na + n=2
+ a) - cosh ( n -1 ) a) +
+ E n ( ( n - 1 ) sinh ( n + 1 ) a - ( n + 1 ) sinh ( n - 1 ) a J , (16)
σ
( m ) _ ap
cosh a - cos P d l ( m - 1 ) sinha d p ° "
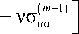
m > 1.
где A n , E n , J – коэффициенты, подлежащие определению. Объединив два уравнения в (12), получим
cosh a - cos в d o aa sinh a д в
Здесь поверхностное напряжение σ β s β по-прежнему остается неизвестным. Для получения граничного условия выразим поверхностное напряжение через известные соотношения (законы Гука и Шаттлворса):
° PP ^ PPPP 6 "" , £ вв e L ° PP V°aa J , (18)
где C β s βββ – тензор модулей поверхностной упругости; £ pp - окружная поверхностная деформация; E , v - соответственно модуль Юнга и коэффициент Пуассона (в данной формуле нет суммирования по повторяющемуся индексу). Из уравнений (18) следует
σ ββ C ββββ
R b LO pP ^aa J , 8 ER
.
Для характерных значений модуля Юнга и констант поверхностной упругости величину R всегда можно выбрать такой, чтобы параметр ε был малым. С учетом выражения (19) граничные условия (12), (17) выражаются следующим образом:
° aa = 8 [ ° PP - V° aa J ,
cosh a - cos P dr -i
°aP = 8---------^L^PP - VOaa J • sinh a dpL J
Решение уравнений (20), (21) получаем путем разложения напряжений по малому параметру ε:
NN
О = £ 8 m О jm ) , b = £ 8 m b ( mm m = 1 m = 1
NN
C = £ 8 m C ( m ) , d = £ 8 m d ( m ) . m = 1 m = 1
Приравнивая члены с равными степенями малого параметра при ε, получаем рекуррентные системы для определения коэффициентов A n , E n , J :
a(0) = 0 c(0) = 0
° aa 0, U aP 0,
„( 1)_J0 ) J1)_ cosha-cospd ( 0 )
°” ", ° sinh a d p° PP , ( )
3. Нулевое приближение (классическая упругость)
Нулевое приближение поставленной задачи (23) является решением задачи классической упругости [26] и имеет вид
- 2 y A (o) = e -------, 2cosh2γ
. (0 ) n 2 sinh 2 у - n sinh у cosh у + e - n y sinh n у _
A n =---------- 2 . ,2 A ----------, n > 2,
2 ( sinh n у - n sinh y )
E(o) =________n sinh2 y________ n 2 (sinh2 ny - n2 sinh2 y)
J ( 0 ) =
1 cosh2γ
В данных выражениях коэффициенты, являющиеся аналогами коэффициентов в уравнении (16), отмечены дополнительным верхним индексом 0, указывающим на соответствие классическому известному решению [26] т.е. решению без учета поверхностных эффектов. Выражения (24) являются нулевым приближением в разложении по параметру ε решения задачи, с учетом поверхностной упругости.
3. Применение рекуррентных соотношений
С помощью соотношений (23) задача сводится к решению набора последовательных задач для каждого члена разложения по малому параметру ε. Если известно ( m - 1)-е решение (т.е. известны а П m - 1), е П m - 1), J ( m - 1)) для компонент напряжения, то аналогично (8), с помощью (5), (6) получаем
(m-1) (m-1) , (m-1) О a°aa )= c0 )+ £cn ) cos n", n=1 (25)
M a o(m-1) = d 0 m-1) + £dnm-1) cos n ", n=1
где cnm-1), dnm-1) имеют вид c0m-1) = 2 A1(m-1) sinh2 y - J(m-1) sinh y cosh y, сПm-1) = 8n 1( J(m-1) sinh y - 4аПm-1) sinh2 y cosh y + ((n +
+ 2)(cosh ( n + 1 ) y sinh y е П m 1 - 1 ) ( n + 1 ) 2 -
- е П m - 1 ) ( n + 1 ) sinh ( n + 1 ) y cosh y +
+ а П m - 1 ) sinh y sinh ( n +1 ) y ( n +1 ) ))) +
+ 5 n 2 ((2 n cosh n y sinh y x
x ( - E nm - 1 ) ( n 2 - 1 ) cosh y - А Пm - 1 ) sinh y ) +
+ 2sinh n y E nm - 1 ) ( n 2 - 1 ) - 2sinh n ysinhycoshy A nm - 1 ) n 2 ) +
+ ( n + 2 ) (cosh ( n + 1 ) y sinh y E n+T'1 ( n + 1 ) 2 - E m1 ( n +
+ 1) sinh ( n + 1 ) y cosh y + A nm । 1' sinh y sinh ( n + 1 ) y ( n + ' ) ))) + + (2 n cosh n y sinh y ( - E nm - 1 ) ( n 2 - 1 ) cosh y - A nm - 1 ) sinh y ) + + 2sinh n y E nm - 1 ) ( n 2 - 1 ) - 2 A nm - 1 ) n 2 sinh n ysinhycoshy) +
+ ( ( n + 2 ) (cosh ( n + 1 ) y sinh y E n + 1 - 1 ) ( n + 1 ) 2 - E nm 1 - 1 ) ( n + +1)sinh ( n +1 ) y cosh y + A nm 1 - 1 ) sinh ( n +1 ) y sinh y ( n +1 ) )) +
+ ( ( n - 2 ) (cosh ( n - 1 ) y sinh y E nm 1 - 1 ) ( n - 1 ) 2 - E nm 1 - 1 ) ( n - -1)sinh ( n -1 ) y cosh y +
+ A ntm ' - ' ) sinh y sinh ( n - 1 ) y ( n - 1 ) )), n > 1. (26)
d0m-1) = -2 A1(m-1) cosh2 y + J(m-1) cosh y sinh y, dnm-1) = 5n 1 (4Anm-1) cosh3 y + J(m-1) sinh y +
+( ( n + 2 ) ( E nm - 1 ) ( n +1 ) cosh ( n +1 ) y sinh y + ( A nm 1 - 1 ) sinh y -
- E nm - 1 ) cosh y)sinh ( n + 1 ) y) -
-
- (2 A nm - 1 ) ( n + 1 ) cosh y cosh ( n + 1 ) y +
+ E nnm - 1 ( n + 1 ) ( ( n + 1 ) 2 - 1 ) cosh ( n + 1 ) ysinhy +
+ ( E n + 1 - 1 ) cosh y( ( n + 1 ) 2 -
-
- 1) + A nm 1 - 1 ) ( ( n + 1 ) 2 + 1 ) sinhy)sinh ( n + 1 ) y))) +
+ 5 n2 (2 A nm cosh2y +
+( ( n + 2 ) ( E n + 1 - 1 ) ( n +1 ) cosh ( n +1 ) y sinh y + ( A nm 1 - 1 ) sinh y -
- E nm - 1 ) cosh y)sinh ( n + 1 ) y) -
-
- (2 A nm - 1 ) ( n + 1 ) cosh y cosh ( n + 1 ) y +
+ E nm 1 - 1 ) ( n + 1 ) ( ( n + 1 ) 2 - 1 ) cosh ( n + 1 ) ysinhy +
+ (Enm1-1) ((n +1)2 -1) cosh y + Anm1-1) ((n +1)2 +1) sinh y )x x sinh (n +1) y)) +
-
+ 2( - sinh y( A n m - 1 ) n cosh n y sinh y + + ( A nm - 1 ) cosh y + E nm - 1 ) sinh y( n 2 -
-
- 1)) sinh n y) + cosh y (2 A n m - 1 ) n cosh n y sinh y +
+ E nm - 1 ) n cosh n y sinh y( n 2 -
-
- 1) + ( E nm - 1 ) ( n 2 - 1 ) cosh y + A nm - 1 ) ( n 2 + 1 ) sinh y ) sinh n y))) + +( ( 2 - n ) ( E nm 1 - 1 ) ( n -1 ) cosh ( n -1 ) y sinh y + ( A n;m 1 - 1 ) sinh y -
- - Enn m1-1) cosh y)sinh (n -1) y) -
- - (2Anm1-1) (n -1) cosh y cosh (n -1) y +
+ E nm 1 - 1 ) ( ( n - 1 ) 2 - 1 ) cosh y +
+ A nm 1 - 1 ) ( ( n - 1 ) 2 + 1 ) sinhy)sinh ( n - 1 ) y)) +
+( ( n + 2 ) ( E nm 1 - 1 ) ( n +1 ) cosh ( n +1 ) y sinh y + ( A n;m - 1 ) sinh y -
-
- E nn m - 1 ) cosh y)sinh ( n + 1 ) y) -
- - (2Anm-1) (n +1) cosh y cosh (n +1) y +
+ E nm - 1 ) ( n + 1 ) ( ( n + 1 ) 2 - 1 ) cosh ( n + 1 ) ysinhy +
+ ( E n m 1 - 1 ) cosh y( ( n + 1 ) 2 -
-
- 1) + A n ( m - 1 ) ( ( n + 1 ) 2 + 1 ) sinh y)sinh ( n + 1 ) y)) +
+ 2( - sinh y( A nm - 1 ) n cosh n y sinh y +
( A nm - 1 ) cosh y + E nm - 1 ) sinh y( n 2 -
-
- 1) sinh n y) + cosh y (2 A nm - 1 ) n cosh y cosh n y +
+ E nm - 1 ) n cosh n y sinh y( n 2 -
-
- 1) + ( E nm - 1 ) ( n 2 - 1 ) cosh y + A nm - 1 ) ( n 2 + 1 ) sinh y ) x
x sinh ny)), n > 1,(27)
где δ nm – символ Кронекера.
Граничные условия (последние два уравнения в (23)) могут быть представлены следующим образом:
MM a °0m) = Esnm)cos ne, a G0e)=Etnm)sin ne, n=0
где
-
(m) _ ,(m-1) _
sn dn V cn, tnm)= 2sinh7 [(n -1) dnm'1^ n +1) dnm-1)-2ndnm-1) cosh y] -
-
-, .v, Г ( n - 1 ) c nm 1 - 1 ) + ( n + 1 ) c nm 1 - 1 ) - 2 nc nm - 1 ) cosh y 1 .(29)
2sinh γ
Последние уравнения в (29) образуют систему для нахождения коэффициентов A(m), E^m), J(m), через
A ( m - 1)
г( m - 0
En ,
J ( m - 1 ) :
aOW = Ersnm) cos nP = 2A - J(m) sinh y cosh y + J(m) sinh y cos в - +т E[( n-1)( n - 2) ^(. y) + 2n=1 + (n +1)( n + 2) fCK. y )- -2(n2-1)coshyfnm) (y)-2sinhyfn*m) (y)]cosnв, M a °am)=rtnm) sin nв= n=1 = -( cosh y (J(m) - 2 A1(m) sinh2y) + f2(m) (y)) sin в + J(m2 cin 2в +-------£[(n-1) fn-m2(Y)- 2n cosh Yf„(m2( y)+ 2 n=2 + (n +1) fn+m)( Y1] s"2ne, (30) где fn m2 ( y ) = АП m2 (cosh (n +1) Y - cosh (n -1) Y2 + 251 + 4 A1 sinh2y cosh Y, n = 2, 2 (n-1) 5n-1 -(1 - 82, n-2)Vn-2 + рП4) = +(1- 82, n-1 ) V n-1 + 2sinh YрП-+ + (-282 n-251 - 82 n-28A1 sinh2y cosh Y + + 482, n-1 cosh y 51 + +Ennm2((n-1) sinh (n +1) y -(n +1) sinh (n -1) y ). (31) +2cosh y82 n-18A sinh2ycosh y), n > 2. Приравнивая коэффициенты при синусах и косинусах в (30), аргументом функции которой является вторая координата β в биполярной системе координат (в дальнейшем для упрощения записи опуская верхний индекс (m)), получаем 250 = 2 A1 sinh2y - J sinh Y cosh Y, 2n5n = vn-1 +Vn+1 - 2 Vn c°sh Y - 2^nsinh Y + 281,n(J sinh Y - -4A1 sinh2y cosh y + 3 f, ( y2), -2tn = Vn-1 +Vn+1 - 2Vncosh Y - -2(-81 n (cosh y(J - 2A sinh2Y) + +f'( Y)) + 82,n 2 J), (32) где V n =(n -1)n (n +1) fn (Y), Vn = nf'( Y). (33) Таким образом, используя уравнения (31), (34), находим оставшиеся неизвестные коэффициенты A1 = ^^, 2sinh2γ A— g (1\|/ +<7(2)Y — Г q^1 p^1q^2 p^3 ]j + q2'2 p'12-2 q214 p'42, nn qn T n qn T n I qn pn qn pn I qn pn qn pn , En = qn2 vn+q2n2vn = = Гq(2111'2 + (4)p232 ] J + q12p(22 + (4)p(42, n > 1, (38) I qn pn qn pn I qn pn qn pn , , где (12 _ n cosh ny sinh Y - cosh Y sinh nY qn " n3cosh2Y-n(n2-1 + cosh2ny), q? = Предположив J известным и применяя процедуру [26], а именно - умножая третье уравнение из (32) на e-”Y и суммируя для всех n, а также учитывая условие сходимости рядов lim vn = 0, получаем n ^м м V1 = J - 2cosh y (J - 2 A1 sinh2Y) eY- 2 e 2Y^tne-nY. (34) n=1 Qn =- (4) qn - sinh γsinhnγ n3 cosh 2y - n (n2-1 + cosh 2ny ) sinhγsinhnγ n3 cosh2Y - n (n2 -1 + cosh 2ny ) sinh ((n +1) y 2 n (n2-1) (1 - n2+ n2 cosh2Y + cosh 2ny) Кроме того, используя уравнение (35) и первое уравнение в (38), определяем коэффициенты J, A1: Из первого уравнения (32) непосредственно следует равенство 2 A1 sinh2y - 50 sinhγcoshγ При n > 1 значения vn, vn вычисляются непосредственно уП = pn j+рП2); vn = рП3)j+рП4),n > 1, (36) где pn*2 = sinh-1 Y(2sinh (n - 2) y - 2cosh y sinh (n -1) y --2cosh y sinh (n - 2) 7eY), p^ = sinh-1 y(4A1 cosh y sinh 2y sinh (n -1) y + +4A1 cosh ysinh2YeY sinh(n - 2) 7- -2e2Ysinh (n - 2) y£tke-k - 2^, sinh (n - k) y), k=1 k=1 Г -2sinh Y, n = 2, p ( 1 = I n 1282 n-2sinh y - 482 n-1 cosh 7 sinh 7 + 2 sinh 7рП-, n > 2, 2 (i “Vrl Et,e-h sinh y - 250cosh y I, sinh3Y ( k=1 J A = 2EM=1tke-k7 coth Y - 50 sinh-2 Y 1 2 (1 + 2cosh2Y 2 . Подставляя найденные коэффициенты (38), (40) в уравнение (27), получим необходимую компоненту напряжения σββ. Полученное решение (38), (40) можно рассматривать как обобщенное решение в [26].
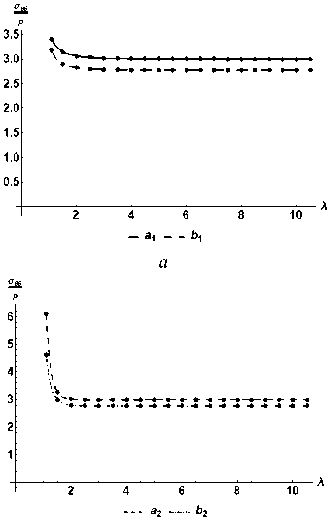
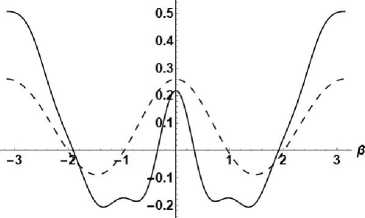
5. Результаты Для решения задачи упругие постоянные материала принимались соответствующими константам алюминия: E = 70,3 ГПа, v = 0,345, а константы, характеризующие свойства поверхности, – упругими постоянными, полученными в [5]: Z = 6,8511 Н/ , p, =-0,376 Н/ , sмsм откуда модуль поверхностной упругости рассчитывался как Свеве = X , + 2^ , = 6,0991 НМ. Концентрации напряжений в точках A, B (см. рис. 1) вычислялись для различных значений относительного расстояния между отверстием и границей полуплоскости X = d/R (рис. 2). Радиус отверстия для расчетов полагался равным R = 2 нм. Рис. 2. Расположение отверстия в полуплоскости Fig. 2. Location of the hole in the half-plane На рис. 3, а, б представлены зависимости концентрации напряжений с учетом и без учета поверхностного напряжения в точках А и В соответственно. Зависимости b1, a1 соответствуют значениям концентрации напряжения с учетом и без учета поверхностного напряжения в точке A; b2, a2, – в точке B (см. рис. 3, б). б Рис. 3. Концентрации напряжений с учетом (a1,2) и без учета (b1,2) поверхностного напряжения: а – в точке А; б – в точке В Fig. 3. Concentration of stresses with account of (a1,2) and without account of (b1,2) of the surface stress, (a) is in the point A, (b) is in point B На рис. 4 представлены зависимости с1, с2, соответствующие значению поверхностного напряжения на контуре отверстия при относительно малом (X = 1,1) и относительно большом (X = 10) расстояниях между отверстием и границей полуплоскости. Из полученных графиков видна разница между концентрациями напряжений с учетом и без учета поверхностного напряжения. При отдалении кругового отверстия от границы полуплоскости наблюдается уменьшение влияния границы полуплоскости на концентрацию напряжения на круговом отверстии. С1---с2 Рис. 4. Поверхностное напряжение в зависимости от координаты β на контуре отверстия Fig. 4. Surface stress depending on coordinate β at the contour of the hole Заключение Получено и исследовано решение задачи теории упругости о полуплоскости, содержащей круговое отверстие с учетом поверхностных эффектов. При помощи разложения в ряды Фурье переменных, представленных в биполярной системе координат, с использованием уравнений теории упругости, дополненных уравнениями поверхностной упругости, рассчитаны величины концентрации напряжений на контуре отверстия. Полученные выражения можно рассматривать как обобщенное решение задачи в традиционной постановке, не учитывающей вклад поверхностных эффектов. Проведены сравнения концентраций напряжений с учетом и без учета вклада поверхностных эффектов в различных точках контура отверстия. Рассмотрен вклад, вносимый поверхностными эффектами в зависимости от относительного расстояния между отверстием и границей полуплоскости. Показано, что, несмотря на довольно простую геометрию, благодаря достаточно малому расстоянию между отверстием и границей полуплоскости значения концентрации напряжений с учетом и без учета поверхностных эффектов существенно отличаются друг от друга. Работа выполнена по теме государственного задания ИПМех РАН АААА-А20-120011690136-2. Acknowledgement The work was carried out on the topic of the state assignment of the IPMech RAS AAAA-A20-120011690136-2.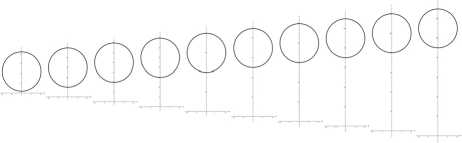
Список литературы Влияние поверхностных эффектов в задаче теории упругости для кругового отверстия в полуплоскости
- Ibach H. The role of surface stress in reconstruction, epitaxial growth and stabilization of mesoscopic structures // Surf. Sci. Rep. - 1997. - Vol. 29. - Р. 195-263.
- Подстригач Я.С., Повстенко Ю.З. Введение в механику поверхностных явлений в деформируемых твердых телах. - Киев: Наук. думка, 1985. - 200 с.
- Исследование физико-механических характеристик на-номасштабных пленок методом наноиндентирования / А.С. Гра-щенко, С.А. Кукушкин, А.В. Осипов, А.В. Редьков // Изв. РАН. МТТ. - 2018. - № 5. - С. 5-14.
- Grekov M.A., Vikulina Y.I. Effect of a type of loading on stresses at a planar boundary of a nanomaterial // Surface Effects in Solid Mechanics. - 2013. - Р. 69-79.
- Греков М.А., Язовская А.А. Эффект поверхностной упругости и остаточного поверхностного напряжения в упругом теле с эллиптическим наноотверстием // ПММ. - 2014. -Т. 78, Вып. 2. - С. 249-261.
- Grekov M.A., Morozov N.F. Surface effects and problems of nanomechanics // J. Ningbo Univ. - 2012. - Vol. 25. - Р. 60-63.
- Eshelby formalism for nanoinhomogeneities / H.L. Duan, J. Wang, Z.P. Huang, B.L. Karihaloo // Proc. Roy. Soc. L., A. -2005. - Vol. 461, № 2062. - Р. 3335-3353.
- Гольдштейн Р.В., Городцов В.А., Устинов К.Б. Влияние поверхностных остаточных напряжений и поверхностной упругости на деформирование шарообразных включений нанометровых размеров в упругой матрице // Физ. мезо-мех. - 2010. - Т. 13, № 5. - С. 127-138.
- Устинов К.Б. О влиянии поверхностных остаточных напряжений и поверхностной упругости на деформирование шарообразных включений нанометровых размеров в упругой матрице // Вестник ННГУ. - 2011. - № 4(5). - С. 2541-2542.
- Nanoporous materials can be made stiffer than non-porous counterparts by surface modification / H.L. Duan, J. Wang, B.L. Karihaloo, Z.P. Huang // Acta materiala. - 2006. - Vol. 54. -Р. 2983-2990.
- Altenbach H., Eremeyev V.A. On the shell and plate theories with surface stresses. Shell Structures. Theory and Applications // W. Pietraszkiewicz, I. Kreja (Eds). Boca Raton, CRC Press. - 2010. - Vol. 2. - Р. 47-50.
- Gandilyan D.V., Ustinov K.B. Influence of surface effects on stress state in a body with two circular holes // IOP Conf. Series: Journal of Physics: Conf. Series. - 2020. - Vol. 1474. -Р. 1-11. DOI: 10.1088/1742-6596/1474/1/012014
- Гандилян Д.В., Устинов К.Б. Влияние поверхностных эффектов в задачах теории упругости для областей, ограниченных неконцентрическими окружностями // Изв. РАН. МТТ. - 2020. [В печати.]
- Wang L. Surface effect on deformation around an elliptical hole by surface energy density theory // Mathematics and mechanics of solids. - 2019. - Vol. 26. - Р. 337-347.
- Grekov M.A., Sergeeva T.S. Interaction of edge dislocation array with biomaterial interface incorporating interface elasticity // International Journal of Engineering Science. - 2020. -Vol. 149, № 103233. - Р. 1-17.
- Kostryrko S., Grekov M., Altenbach H. Stress concentration analysis of nanosized thin-film coating with rough interface // Continuum Mech. Thermodyn. - 2019. - Vol. 31. - Р. 1863-1871. DOI: 10.1007/s00161-019-00780-4
- The effects of surface elasticity on the thermal stress around a circular nano-hole in a thermoelectric material / Kun Song, Hao-Peng Song, Peter Schiavone, Cun-Fa Gao // Mathematics and mechanics of solids. - 2019. - Р. 3156-3166.
- Об учете масштабных эффектов при моделировании механических и трибологических свойств двухфазных микро- и наномодифицированных полимерных покрытий / В.М. Бузник, С.А. Лурье, Д.Б. Волков-Богородский, А.Г.Князева, Ю.О. Соля-ев, Е.И. Попова // Вестник Пермского национального исследовательского политехнического университета. Механика. -2015. - № 4. - С. 36-54.
- Hashin Z. Thermoelastic properties of particulate composites with imperfect interface // J. Mech. Phys. Solids. - 1991. -Vol. 39, № 6. - Р. 745-762.
- Ustinov K.B., Goldstein R.V., Gorodtsov V.A. On the modeling of surface and interface elastic effects in case of eigenstrains // Models, Simulations and Applications. Series: Advanced Structured Materials / Altenbach H., Morozov N.F., Eds. -2013. - XV. 30. - Р. 167-180.
- Гольдштейн Р.В., Городцов В.А., Устинов К.Б. О построении теории поверхностной упругости для плоской границы // Физ. Мезомех. - 2013. - Т. 16, № 4. - С. 75-83.
- Городцов В.А., Лисовенко Д.С., Устинов К.Б. Шарообразное включение в упругой матрице при наличии собственных деформаций с учетом влияния свойств поверхности раздела, рассматриваемой как предел слоя конечной толщины // Известия Российской академии наук. Механика твердого тела. - 2019. - № 3. - С. 30-40.
- Dyskin A.V., Germanovich L.N., Ustinov K.B. Asymptotic solution for long cracks emanated from a pore in compression // International Journal of Fracture. - 1993. - Vol. 62. - Р. 307-324. DOI: 10.1007/BF00017238
- Ustinov K.B. Asymptotic solution for long cracks emanated from a hole in bi-axial loading // International Journal of Fracture. - 1994. - Vol. 68. - Р. 73-77. DOI: 10.1007/BF00013075
- Jeffery G.B. Plane stress and plane strain in bipolar coordinates // Phil. Trans of the Roy Soc of London ser. A. - 1921. -Vol. 221. - Р. 265-293.
- Уфлянд Я.С. Биполярные координаты в теории упругости. - М.; Л.: Гостехиздат, 1950. - 232 с.
- Chin-Bing Ling. On the stresses in a plate containing two circular holes // J. Appl. Phys. - 1948. - Vol. 19, № 1. -Р. 77-82.
- Gurtin M.E., Murdoch A.I. A continuum theory of elastic material surfaces // Arch. Ration. Mech. and Analysis. -1975. - Vol. 57, № 4. - Р. 291-323.
- Spiegel M., Lipschutz S., Spellman D. Vector Analysis (2nd Edition). McGraw Hill, 2009. - 254 p.
- Shuttleworth R. The surface tension of solids // Proc. Phys. Soc. - 1950. - Vol. A63. - Р. 444-457.
- Vikulina Y.I., Grekov M.A., Kostyrko S.A. Model of film coating with weakly curved surface // Mechanics of Solids. -2010. - Vol. 45, № 6. - Р. 778-788.


