Влияние предварительного смещения в зоне контакта на работоспособность подшипников скольжения
Автор: Меновщиков В.А., Щелканов С.И., Кайгородов А.С., Шаронов А.А.
Журнал: Вестник Красноярского государственного аграрного университета @vestnik-kgau
Рубрика: Техника
Статья в выпуске: 6, 2012 года.
Бесплатный доступ
В данной статье излагается теория определения смещения тел в контакте подшипника скольжения с учетом влияния шероховатости поверхностей. Рассматриваются явления в момент, предшествующий началу движения, так называемое предварительное смещение, под которым обычно понимают процессы, происходящие на контакте при переходе к скольжению.
Подшипник скольжения, контакт, предварительное смещение, трение, коэффициент трения, коэффициент жесткости, шероховатость поверхностей, работоспособность
Короткий адрес: https://sciup.org/14082464
IDR: 14082464 | УДК: 621.517,681.142.36
Текст научной статьи Влияние предварительного смещения в зоне контакта на работоспособность подшипников скольжения
Введение. Физическая картина работы цилиндрического подшипника скольжения, несущего радиальную нагрузку, хорошо отображается диаграммой Герси-Штрибека [1, 2]. Диаграмма строится на основе экс- периментальных данных (рис. 1), особый интерес на данной кривой представляет участок (1-2), который соответствует страгиванию вала из состояния покоя. В этой зоне имеет место «сухое трение» со значительным коэффициентом трения, сопровождаемое высокой интенсивностью изнашивания и возможностью возникновения задира или заедания. Началу движения вала во втулке предшествует предварительное смещение в контакте.
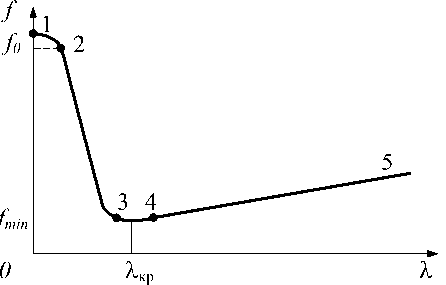
Рис. 1. Диаграмма Герси-Штрибека
Объект исследования. Объектом нашего исследования послужил подшипник скольжения, используемый во многих отраслях промышленного производств.
Цели и задачи исследования. Соприкосновение вала и втулки в подшипнике скольжения можно рассматривать как систему, обладающую определенными физическими свойствами. Изучение свойств этой связи, её формирования и разрушения имеет большое значение для анализа явлений, происходящих в контакте.
Наибольший интерес представляют явления, возникающие на контакте, в момент, предшествующий началу движения, так называемое предварительное смещение, под которым обычно понимают процессы, происходящие на контакте при переходе к скольжению. В данный период времени присутствует граничное трение, наличие как металлического контакта, так и жидкостного.
Если к телу 1 , находящемуся в контакте с телом 2 (рис. 2), приложить сдвигающую силу F , то до начала скольжения появится смещение, равное предварительному смещению A в сторону действия силы F . Значение силы F в области предварительного смещения зависит от силы трения покоя F тр .
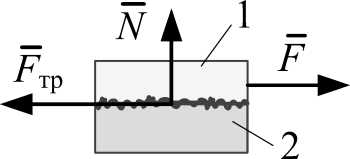
Рис. 2. Контакт шероховатых тел
Закон изменения силы трения в зависимости от перемещения представлен на рисунке 3. При этом в области предварительного смещения сила FF тр . Сила трения на участке ( о – а ), (следуя рис. 3), подчиняется закону
F тр = cx , (1) где c – коэффициент жесткости контактирующих поверхностей [Н/м], x – смещение тела 1 в пределах от 0 до ∆.
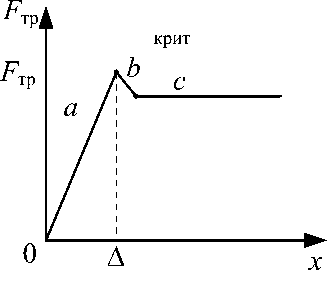
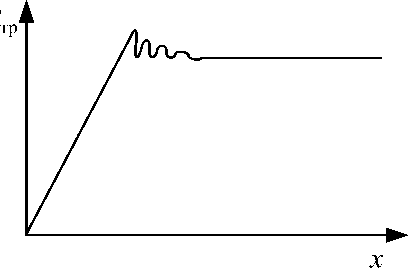
Рис. 3. Закон изменения силы трения в зависимости от перемещения
Дифференциальное уравнение движения тела 1 имеет вид
mx =F - cx.
Преобразуем уравнение (2) к виду
mXdx = F-cx dx.
Интегрируя уравнение (3) при начальных условиях: t= 0 , x 0 = 0 , x 0 = 0 , получим
Fc2 x = 2 x x
mm
Решаем уравнение (4) относительно t
dx
c 2 F 2
x 2 x
mm
.
mc
arcsin 1 x C .
Значение C определим из (5) при соответствующих начальных условиях C
учетом значения постоянной
t
mc arcsin 1 x cF
, тогда с
Используя уравнение (6), выразим перемещение x тела 1 в зависимости от времени
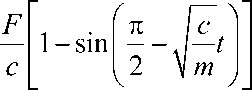
Анализ движения тела 1 показывает, что на участке ( b – c) при FF тр движение подобно зату-
F хающим колебаниям (рис. 3,б). Амплитуда этих колебаний равна A= , т.е. максимальная амплитуда ко- лебаний равна предварительному смещению ∆.
Принимая x = A , из уравнения (7) определим время, за которое произойдет предварительное смещение
t
п . с .
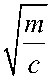
c arccos 1 —л.
.
В формуле (8) подлежат определению коэффициент жесткости c и величина предварительного смещения ∆. Данные параметры зависят от физико-механических свойств контактирующих материалов и геометрии поверхностей (шероховатость, волнистость).
При скольжении контактирующих поверхностей вначале происходит процесс приработки, в результате которого шероховатость поверхностей при дальнейшей эксплуатации остается почти постоянной. Поскольку изменение микрогеометрии поверхности еще недостаточно изучено, то, по-видимому, контакт следует рассматривать при условии сохранения приработочной шероховатости. Следует также отметить тот факт, что после приработки контакт шероховатостей поверхностей будет в основном упругим, в крайнем случае упругопластическим, с преобладанием упругих деформаций. При упругом контакте приложение тангенциальной силы приводит к смещению точки с т к поверхности соприкасающихся тел.
Допустим, что после приработки неровности соприкасающихся поверхностей равновысотны и имеют сферическую форму. Следует отметить, что нагрузка в подшипнике скольжения распределяется в основном по наибольшим контурным площадям, полученным после приработки наиболее выступающих неровностей [3]. Такие неровности деформируются в упругой области и имеют контурные площади контакта ( А с ), изменение площади которых при многократном нагружении не превышает 5 % [4].
Рассмотрим контакт сферических выступов неровностей (рис. 4).
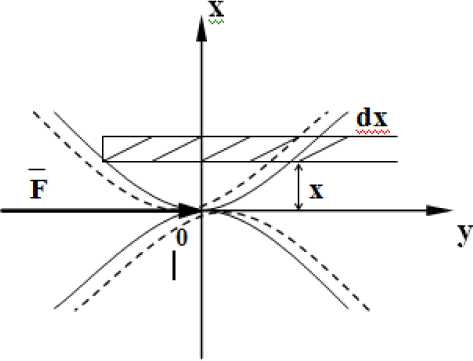
Рис. 4. Расчетная схема
Под действием силы F происходит упругое смещение неровностей в точке O . Для сечения с координатой x смещение y определяется уравнением
E Jzdx2 M(y) ,или E J F y ,
dy dy
2ЕЕ где E – приведенный модуль нормальной упругости, Е = 12;
Е 1 + Е 2
J z – момент инерции, определяемый по формуле [6], J
71-z4
.
Выражая z через R и y , получим
T _ 71 2
J z 4 y 2 R-y
Подставляя выражение (10) в уравнение (9), имеем
.
d 2 x
4F
dy 2 7Г Ey 2 2 R-y 2
Интегрируя уравнение (11), получим
dx
F
F1 ln dy 7CE R2
2R-y
y R 2R-y
+ С 1 .
.
dx
При начальных данных x = 0 , y =R , 00 dy
2F
0 = 0 С 2 F
1 Л ER 2
.
Решая уравнение (12) относительно x , найдем смещение ∆. При y= 0
2 F
A= x =
71 ER .
Вводя в формулу (13) число основных неровностей на контакте по теореме Кастильяно [ 6 ] при n >1, получим
A 1 = x 1
2F
2n 1 ТС ER .
Применяя (14) в уравнении (8) и заменяя c= E S . (здесь S – суммарная контурная площадь), получим
tп.с. 2 arccos
k
2SF
1+----------7tRE 2n-1
.
При этом в формуле (15) P < F, т.е. значение силы P соответствует силе трения в точке b (см. рис. 3), а F будет равной силе трения покоя в точке a .
Сдвигающая сила P может быть определена по формуле [ 5 ]
2 71 a
P = IfTp dpdФ,
где t – напряжение сдвига, определяемое из выражения
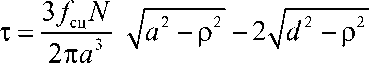
причем cd
.
После подстановки (17) в (16) имеем
P f N a3 b3 2 d3 c3
a
где a , b , c , d – параметры сдвигаемых сферических неровностей.
Выводы. Таким образом, первоначальный сдвиг шероховатых поверхностей в основном зависит от коэффициента сцепления неровностей, который в значительной степени определяется микрогеометрией и физико-механическими свойствами контактирующих поверхностей.


