Влияние примесей на электросопротивление меди и алюминия

ВЕСТНИК Мордовского университета | 2014 | № 1-2

В качестве дисперсных и волоконных наполнителей композиционных материалов довольно часто используют металлы и сплавы. Такие добавки могут существенно изменить электрофизические свойства материала. Естественно, степень и характер этого влияния зависят от свойств самих металлов. К числу наиболее часто применяемых в качестве металлических наполнителей относятся медь и алюминий.

Основной физической характеристикой проводящих материалов является электропроводность, однако к этим материалам предъявляются и дополнительные требования по механическим свойствам, прежде всего прочности. Повышение прочности обычно достигается введением примесных элементов, но они, как правило, приводят к увеличению электросопротивления. Двойное противоположно направленное действие примесей заставляет искать пути оптимального их использования. Для этого необходимо детально исследовать механизмы влияния примесных атомов на комплекс физических свойств. В этом направлении на настоящий момент нет полной ясности.

В настоящей работе проведен анализ влияния температуры и примесей на основные электропроводящие материалы

кабельного производства – алюминий и медь – с использованием литературных данных о термических и электрических свойствах этих металлов.

В приближении времени релаксации [1] электросопротивление изотропного металла вычисляется по формуле:

∗ m ρ=        , ne ТП)

где т ( п ) - время релаксации при энергии электрона, равной энергии Ферми η ; n - концентрация электронов в металле; e – заряд электрона; m ^∗ -эффективная масса электрона, или

Р =

12^2 Nq e2   A

где ħ – постоянная Планка; е – заряд электрона; N – число атомов в единице объема; q – сечение рассеяния при столкновении электронов проводимости с атомами; А – площадь поверхности Ферми [2].

A =

8 n m

п

= 4 п ³1 n I

I п )

,

где m – масса электрона; n ₀ – плотность электронов проводимости, равная произведению числа валентных электронов в атоме на число атомов в единице объема.

В уравнения (1–2) входят параметры, характеризующие кристаллическую (N) и электронную (А, η) структуру металла в целом, и параметр q, который, согласно своим свойствам, может быть отнесен к единичному конкретному атому, например, атому примеси. По этой причине в дальнейшем анализе мы опирались на формулу (2). В чистом металле все атомы одинаковы (неразличимы) и величина q имеет единственное (в статистическом понимании) значение. В металлических растворах ситуация осложняется за счет наличия рассеивающих центров двух или более видов. Тогда в (1) под параметром q необходимо понимать некоторое эффективное сечение рассеяния, которое вычисляется по следующей формуле:

∗ e ² A q ^∗ = ρ . (4)

12 п 3 2 N

Определение эффективного сечения рассеяния, согласно выражению (3), имеет смысл только в том случае, если проводимость металла или сплава носит чисто электронный характер, а также в случае, когда электронная структура описывается моделью одной зоны со сферической (или почти сферической) поверхностью Ферми [3]. Такая модель, как известно, приемлема для описания электрических свойств металлов первой группы периодической системы элементов, а также для большинства металлических расплавов [4]. В твердых поливалентных металлах, к которым относится алюминий, поверхность Ферми располагается в двух и более зонах, поэтому проводимость этих металлов носит смешанный электронно-дырочный характер. Следовательно, для описания электрических свойств таких, даже чистых, металлов необходимо вводить по крайней мере два параметра, характеризующих рассеяние электронов и дырок: q_- и q₊ .

Большинство примесей в алюминии и меди, используемых при производстве кабелей, находятся в состоянии твердого раствора. В этом случае для описания взаимодействия электронов проводимости с атомами необходимо четыре парциальных параметра рассеяния, что крайне затрудняет анализ экспериментальных данных с использованием даже простейших моделей. Однако использование представления об эффективном сечении рассеяния может дать некоторую информацию по интересующему нас вопросу.

В работе [5] получено соотношение для расчета энтропии однокомпонентного вещества в виде:

Серия «Естественные и технические науки»

5 = Nk ln(1 + х о T п ³),      (5)

где N – число атомов; k – постоянная Больцмана; χ ₀ – постоянная, определяемая сортом вещества и независящая от температуры.

Величина σ, названная автором [5] параметром беспорядка, для кристаллов практически равна среднеквадратичной амплитуде тепловых колебаний. Практика показала, что параметр χ ₀ следует рассматривать как подгоночный и рассчитывать его на основе экспериментальных данных. Чтобы исключить χ ₀, преобразуем (5):

£ 2 = T^ exp( S / R ) - 1 ст ₀ ² T [ exp( S ₀/ R ) - 1

Формула (6) была применена нами для расчета значений амплитуды тепловых колебаний атомов алюминия и меди в диапазоне температур от 0 К до температуры плавления. Для расчетов использовались данные по теплоемкости [6]. В качестве реперной была взята температура Т0 = 250 К. Энтропия вычислялась по стандартной формуле:

S ( T ) = ∫ ₀ ^{T C} _T ^{( T )} dT ,          (7)

где С ( Т ) – теплоемкость.

На рис. 1–2 показаны температур-

σ ²

ные зависимости параметра 2 и отно-

σ0      p сительного электросопротивления p0

меди и алюминия, ρ – электросопротив- где Т0 – некоторая реперная температура, а S0 и s0 – значения энтропии и параметра σ при этой температуре.

ление при температуре Т , ρ ₀ – электросопротивление при реперной температуре Т₀.

ВЕСТНИК Мордовского университета | 2014 | № 1-2

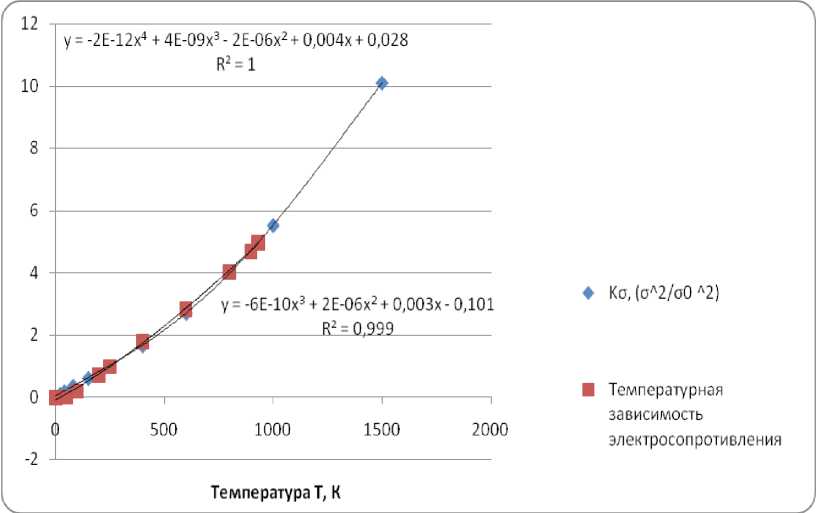
Рис.

и электросопротивления от температуры для Al

1. Зависимость

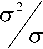
Согласно рисунку, зависимости σ ² (Т) и ρ (Т) для обоих исследованных металлов имеют общий характер: значения этого параметра нелинейно возрастают с увеличением температуры. Следовательно, электросопротивление чистых металлов практически полностью определяется смещением атомов из положений равновесия при тепловых колебаниях, и пропорционально квадрату амплитуды колебаний.

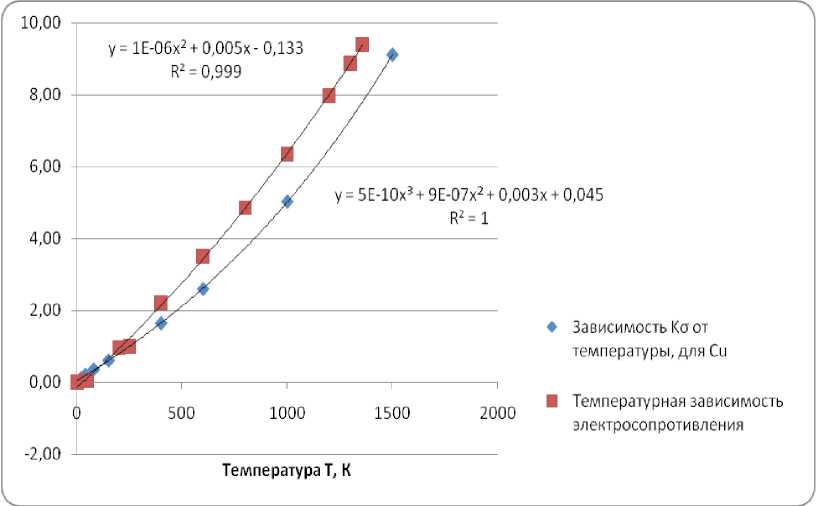
Рис.

и электросопротивления от температуры для Cu

2. Зависимость

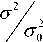
На рис. 3 приведены данные по влиянию примесей на электросопротивление меди, взятые из работы [7]. Из графика видно, что даже при добавлении к меди 0,1 % серебра, металла с меньшим удельным электрическим сопротивлением, общее сопротивление сплава возрастает на несколько процентов. Особенно резко снижают электропроводность меди такие примеси, как фосфор, железо, кобальт и мышьяк.

Серия «Естественные и технические науки»

На рис. 4 приведены данные по влиянию примесей на электропроводность алюминия [8]. Как видно, наиболее сильное отрицательное влияние на электросопротивление алюминия оказывают примеси Сг, V, Мn и Ti.

Влияние примесей на электросопротивление металлов может быть обусловлено несколькими факторами. Во-первых, размеры атомов растворителя и растворенного элемента раз- личаются, что приводит к смещению атомов растворителя из их положений равновесия пропорционально разности атомных радиусов. Следовательно, чем сильнее отличаются атомные радиусы, тем большего увеличения электросопротивления можно ожидать. В таблице приведены значения атомных радиусов алюминия, меди и некоторых элементов, часто являющихся примесями в них.

ВЕСТНИК Мордовского университета | 2014 | № 1-2

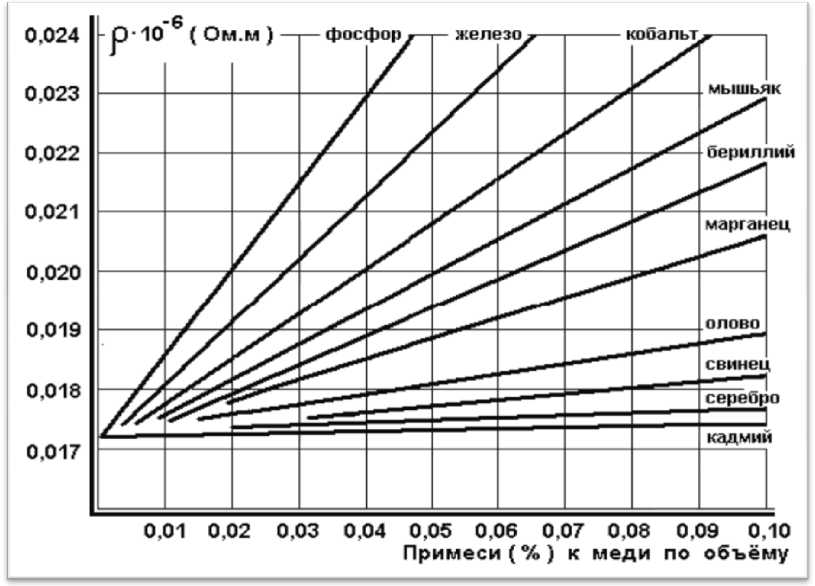
Р и с . 3. Влияние примесей на электросопротивление меди [8]

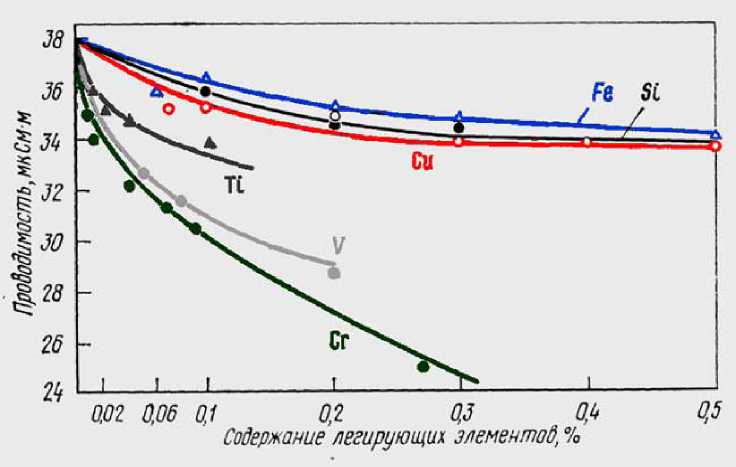
Рис. 4. Влияние примесей на электросопротивление алюминия [9]

Сопоставляя данные таблицы и талла и легирующего элемента не яв-рис. 3–4, мы сделали вывод, что раз- ляется основной причиной увеличения ность атомных радиусов основного ме- электросопротивления.

Т а б л и ц а

Характеристики атомов основного и примесных элементов

Элемент	Атомный радиус				Электронная конфигурация
	[7]	[10]	Ср.	∆r
B	0,725	0,910	0,818	0,613	2s22p1
Be	1,140	1,130	1,135	0,295	2s2
Ni	1,243	1,240	1,242	0,189	3d84s2
Fe	1,239	1,260	1,250	0,181	3d64s2
Cr	1,246	1,270	1,258	0,172	3d54s1
Cu	1,275	1,280	1,278	0,153	3d104s1
V	1,314	1,340	1,327	0,103	3d34s2
Mn	1,365	1,300	1,333	0,097	3d54s2
Zn	1,330	1,390	1,360	0,070	3d104s2
Al	1,430	1,430	1,430	0,000	3s23p1
Nb	1,426	1,450	1,438	-0,010	4d45s1
Ti	1,475	1,460	1,468	-0,050	3d24s2
Si	1,654	1,340	1,497	-0,070	3s23p2
Mg	1,593	1,600	1,597	-0,170	3s2
Zr	1,616	1,600	1,608	-0,180	4d25s2
Tl	1,700	1,710	1,705	-0,280	6s26p1
Bi	1,600	1,820	1,710	-0,280	6s26p3
Pb	1,747	1,750	1,749	-0,320	6s26p2
Ca	1,970	1,970	1,970	-0,540	4s2

Серия «Естественные и технические науки»

Следовательно, примеси могут оказывать влияние на электропроводность посредством влияния на концентрацию электронов проводимости n (а через нее – на площадь поверхности Ферми) или на эффективное сечение рассеяния.

Согласно приведенным в последнем столбце табл. электронным конфигурациям атомов, введение большинства примесей должно привести к увеличению концентрации электронов проводимости как в алюминии, так и в меди. Следовательно, изменение концентрации электронов проводимости не является непосредственным решающим фактором при объяснении влияния примесей на электросопротивление меди и алюминия.

Таким образом, основной фактор влияния примесей на электропроводность алюминия и меди – эффективное сечение рассеяния. В работах [9; 10] при анализе данных по электросопротивлению и термо-эдс было выяснено, что примеси по-разному влияют на сечения рассеяния электронов и дырок в поливалентных металлах. Это может привести к достаточно сложной температурной и концентрационной зависимостям этих свойств. Возможно, именно с этим фактором связано и влияние примесей на электросопротивление алюминия и меди.

ВЕСТНИК Мордовского университета | 2014 | № 1-2