Влияние радиуса скругления тепловой канавки на допустимую разность температур по радиусу ротора паровой турбины

Для большей гарантии исключения прогиба вала паровой турбины на валу с определенным шагом выполняют тепловые канавки – узкие прорези глубиной 8 – 12 мм. Благодаря наличию тепловых канавок при сильном разогреве вала он имеет возможность свободно расширяться в осевом направлении. При этом не происходит изгиба вала [1].

Однако, наличие узких прорезей приводит к уменьшению диаметра вала турбины в сечении тепловой канавки, что влечет за собой увеличение напряжения, т.е. тепловая канавка является концентратором напряжений.

Коэффициент концентрации напряжений для одиночной канавки рассчитывается по формуле Нейбера [2]:

к = 1 + 2 J | , где h - глубина канавки, р - радиус скругления тепловой канавки.

При пусках и остановах паровой турбины её равномерно прогревают, либо охлаждают. Если процесс прогревания или охлаждения идет не равномерно, то в деталях, в частности в роторе, возникают температурные напряжения.

Процесс возникновения температурных напряжений показан на рис.1. Если некоторый стержень длиной I, имеющий температуру Т₀, нагреть дополнительно на величину ДТ то он удлинится на величину М = а_т1ДТ (рис.1, а), но никаких напряжений в нем не возникнет. Если, однако, перед нагревом стержень закрепить между двумя жесткими плитами (рис. 1, б), то они будут препятствовать линейному расширению стержня и в каждом его сечении возникнет деформация сжатия, величина которой равна:

£т = —р = —атДТ, и в соответствии с законом Гука появятся напряжения сжатия:

а = Ее_т = —Еа_тДТ, где Е - модуль упругости, а_т - коэффициент линейного расширения.

Если тот же свободный стержень нагреть до температуры Т = Т0 + ДТ (рис.1, в), затем зажать между двумя жесткими плитами и охладить до температуры Т = Т0 (рис.1, г), то будет происходить уменьшение линейного размера стержня. Жесткие плиты не дадут ему сделать это, и стержень окажется растянутым на величину Д/т. В этом случае возникнут напряжения растяжения:

с = ЕсстМ.

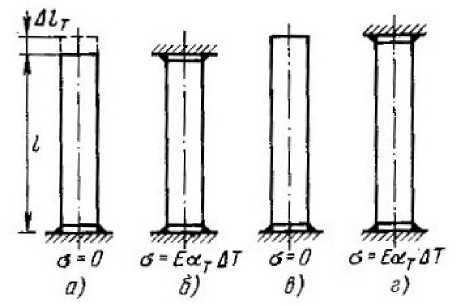
Рисунок 1. Возникновение температурных напряжений в стержне, зажатом между жесткими плитами

Очевидно, что возникающие температурные напряжения зависят от характера распределения температуры в детали. В подавляющем большинстве случаев распределение температуры в детали имеет параболический характер [1]. Например, изменение температуры по радиусу ротора, как это показано на рис.2 описывается соотношением [1]:

Т = То + Aff^0)9,

0      П-^

где q - показатель параболы.

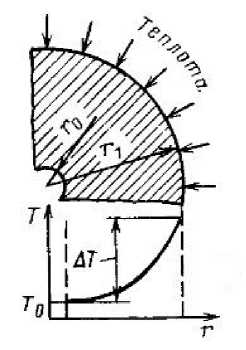
Рисунок 2. Характер изменения температуры в сечении ротора турбины при подводе теплоты

В большинстве случаев q = 2 ^ 4.

При подводе теплоты к валу турбины наибольшие напряжения возникают на обогреваемой поверхности, где температура на величину ДТ больше, чем температура на необогреваемой поверхности.

Так как металл будет прогреваться быстрее в месте подвода теплоты, чем последующие «слои», то его скорость расширения металла будет больше. В связи с этим, нижние «слои» будут препятствовать нормальному расширению металла на поверхности и в них возникают напряжения сжатия, которые можно рассчитать по формуле:

о =

—

q  атЕ q+21—^

ДТ, где

^ - коэффициент поперечного сужения (коэффициент Пуассона) - характеристика металла, указывающая, какую долю продольного удлинения составляет поперечное сужение. Для сталей в зависимости от марки ^ = 0,27^0,32 [1].

Для оценки влияния радиуса скругления на допустимую разность температур по радиусу ротора на поверхности ротора из стали марки Р2М выполнены тепловые канавки (рис. 3) глубиной h = 8 мм, и радиусами скругления ρ = 1,0; 2,0; 3,0 мм.

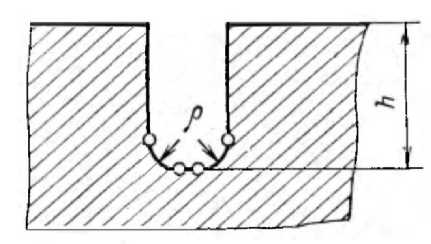
Рисунок 3. Размеры тепловой канавки

Показатель параболы q = 3.

Коэффициент Пуассона μ = 0,3.

Модуль упругости Е = 1,96 ∙ 10⁵ МПа.

Коэффициент линейного расширения а _т = 13,7 • 10^-6 1/К, при T = 773 К.

Предел текучести о _s = 540 МПа [1] - выбрали именно предел текучести, потому что после превышения данного предела появляются пластические деформации.

При р = 1,0 мм:

Коэффициент концентрации напряжений для одиночной канавки:

к = °к = 1 + 2 • ^=1 + 2- р = 3,828, так как он                 р              л/1

о"к = к • он, где ок - напряжения, возникающие в канавке;  стн - напряжения, возникающие на поверхности ротора.

Напряжения, возникающие на поверхности ротора, при условии, что в тепловой канавке напряжения не превышают предел текучести: о540

он = — =---= 141,05 МПа;

н    к3,828

Допустимая разность температур по радиусу ротора:

д^.     ° н '( ^1- м^),(д ⁺²⁾ .

ат-E-q’ д^ < 141,05-(1-0,3)-(3 + 2).

13,7-10-6-1,96-105-3 ;

△Т < 61,283 К.

При р = 2,0 мм:

к = 3;

он = 180 МПа;

△Т < 78,206 К.

При р = 3,0 мм:

к = 2,633;

ан = 205,09 МПа;

AT < 89,107 К.

Таблица 1

Результаты оценки влияния радиуса скругления тепловой канавки на допустимую разность температур по радиусу ротора

	Радиус скругления, мм
	ρ = 1,0	ρ = 2,0	ρ = 3,0
Коэффициент концентрации напряжений для одиночной канавки	3,828	3	2,633
Напряжения, возникающие на поверхности ротора, при условии, что в тепловой канавке напряжения не превышают предел текучести, МПа	141,05	180	205,09
Допустимая разность температур по радиусу ротора, К	61,283	78,206	89,107

Как видно из таблицы, увеличение радиуса скругления тепловой канавки с 1 мм до 2 мм ведет к увеличению допустимой разницы температур AT по радиусу ротора (разность температур на поверхности радиусом r 1 и на поверхности радиусом r₂ ) на 27,6 %, а увеличение радиуса скругления тепловой канавки с 2 мм до 3 мм ведет к увеличению допустимой разницы температур AT по радиусу ротора на 13,9 %.