Влияние распределения контактных напряжений на утечки через торцевое уплотнение

Введение. В узлах аэрокосмической техники, а также в стендах для испытаний элементов аэрокосмических конструкций широко используются неподвижные резиновые уплотнения для герметизации объемов с высокими давлениями [1]. Утечки через круглое торцевое уплотнение могут быть определены [2] по формуле

n A p 3G

Q = VoR- exp(- n), (1) 6 In R1/ R2 n 0 z kE где Q - утечки через уплотнение; R 1 и R2 - наружный и внутренний радиусы прокладки; Ap - перепад давлений; п — вязкость уплотняемой среды; у0 - коэффициент формы микронеровностей; RZ - параметр шероховатости уплотняемой поверхности; оn - нормальное напряжение на контакте; E - модуль упругости уплотнителя; k - коэффициент, учитывающий особенности конкретной физической модели (0,05-0,3).

Формула (1) получена из уравнений Навье–Стокса для ламинарного течения газа без учета центробежных сил . Из анализа приведенного выражения для определения утечек следует , что они в значительной степени зависят от величины напряжений в зоне контактирования уплотнителя с уплотняемой поверхностью . Величина этого напряжения , как известно [2; 3], зависит как от давления предварительного поджатия p_{k o} , так и в некоторых конструкциях уплотнений от перепада давлений уплотняемой среды Δ p . При использовании формулы (1) обычно используется среднее значение нормальных напряжений .

Из практики эксплуатации уплотнений различных конструкций [4-6] известно, что форма контактирующих поверхностей, а следовательно, и форма эпюры напряжений в зоне контакта значительно влияют на величину утечек. В литературе, однако, практически отсутствуют сведения о влиянии на утечки распределения контактных напряжений по ширине площадки контакта. Использование современных конечно-элементных программ позволяет с высокой точностью рассчитать распределение контактных напряжений в зоне контакта с учетом вязкоупругих свойств уплотнения, явлений релаксации и ползучести [7-12]. Таким образом, установление связи между величиной утечек и распределением контактных напряжений позволит, во-первых, точнее рассчиты- вать величину утечек для существующих уплотнений, а во-вторых, оптимизировать форму уплотнений при их проектировании в каждом конкретном случае.

Установка для исследований и методика испытаний. Схема установки для изучения утечек через торцевое уплотнение представлена на рис. 1, внешний вид элементов конструкции установки с фотографиями кольцевых инденторов и их схемами приведен на рис. 2.

Объектом исследования являлось неподвижное торцевое кольцевое уплотнение 1 (рис. 1). При испытаниях кольцевая прокладка из резины зажималась между двумя стальными фланцами 3 и 4 . Во внутреннюю полость уплотнения подавался воздух под давлением 0-1 , 5 МПа . Воздух подавался из газового баллона 7 , где его давление составляло 15 МПа , через газовый редуктор 8 . Точность регулировки и измерения избыточного давления составляла 0 , 01 МПа . Утечки измерялись с наружной стороны прокладки (штуцер 10 ) [13].

Кольцевая прокладка прямоугольного сечения из резины 1 имела наружный диаметр 36 мм , внутренний диаметр 16 мм и высоту 4 мм . Она помещалась в кольцевую канавку на стальном фланце 3 глубиной 2 , 6 мм и диаметрами, равными диаметрам прокладки, и приклеивалась . В противоположный фланец закладывались сменные кольцевые инденторы 2 различной формы (3 варианта - см . рис. 2) .

В первом варианте это был прямоугольный выступ шириной 1 , 8 мм с радиусами 0 , 3 мм по краям (ширина плоской части 1 , 2 мм) . Во втором варианте сечение выступа представляло собой равносторонний треугольник с углом у вершины 90° и радиусом у вершины 0 , 5 мм . В третьем варианте это был прямоугольный выступ шириной 0 , 4 мм с радиусом у вершины 0 , 2 мм . Шероховатость поверхности выступов соответствовала Ra = 1 , 25 мкм . Статический модуль упругости резины составлял Е = 3 , 2 МПа . Средний диаметр выступов во всех вариантах был один и тот же и составлял 25 , 8 мм , а высота - 1 , 8 мм . Давление предварительного поджатия p k o создавалось шестью болтовыми соединениями , расположенными равномерно по окружности фланцев . Перемещение регулировалось и измерялось инструментальными измерительными плитками 6 (рис. 1) с точностью 0 , 01 мм .

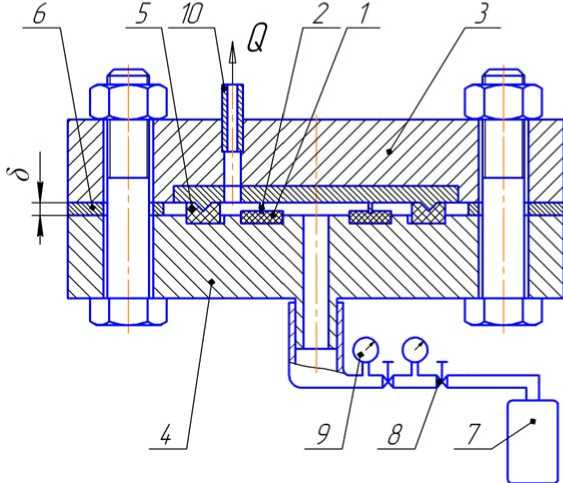
Рис. 1. Схема установки для изучения утечек через торцевое уплотнение

Рис. 2. Внешний вид элементов конструкции установки и схемы вариантов инденторов

Вариант 1

Вариант 2

Вариант 3

Методика испытаний заключалась в следующем . В канавку на стальном фланце устанавливалась резиновая кольцевая прокладка . Посредством болтовых соединений и мерительных плиток 6 устанавливалось заданное минимальное внедрение δ кольцевого выступа – индентора , изготовленного по первому варианту , в резину . При этом непосредственно регулировался и измерялся наружный зазор между фланцами .

Затем через газовый редуктор во внутреннюю полость уплотнения подавалось заданное минимальное давление воздуха и производилось измерение утечек. После этого давление воздуха увеличивалось, и измерение утечек повторялось. После измерения утечек во всем диапазоне давлений при первом минимальном значении внедрения индентора его величину увеличивали до следующего значения, и все измерения повто- рялись. В той же последовательности проводились измерения для двух других вариантов инденторов. Для каждого нового варианта выступа и параллельных опытов устанавливалась новая резиновая прокладка.

Результаты экспериментальных исследований. В результате исследований были получены экспериментальные зависимости величины утечек от избыточного давления при различных величинах внедрения выступа в резину . Эти зависимости для всех трех вариантов формы индентора представлены на рис . 3–5 . Анализ результатов показывает , что для всех вариантов формы инденторов и при всех значениях внедрения индентора в резину наблюдается линейная зависимость величины утечек от перепада давлений уплотняемой среды , что соответствует формуле (1) .

Использование геометрического коэффициента подобия позволяет привести зависимости , представленные на рис . 3-5, к базовому варианту (вариант 1) . На рис . 6 в качестве примера приведены результаты такого пересчета для внедрения индентора 5 = 0 , 2 . На этом рисунке зависимость для первого варианта взята из рис . 3 без изменений , все значения перепадов давлений из рис . 4 и 5 для второго варианта разделены на 2 , 17 (табл . 1) , а для третьего варианта - разделены на 4 , 37 (табл . 1) . Такое приведение дает возможность исключить влияние на утечки всех факторов, кроме концентрации напряжений , создаваемой индентором в вариантах 2 и 3 . На рис . 6 видно , что утечки во втором варианте примерно в 2 раза меньше , чем в первом (базовом) варианте , а в третьем варианте различие достигает 10 раз . Таким образом, использование формулы (1) для расчета утечек без учета возникающих максимальных напряжений в конструкциях уплотнений может привести к ошибкам, достигающим 1 000 %.

Анализ выражения (1) позволяет определить превышение максимальных напряжений σ max над средними напряжениями о m . Это может быть выполнено путем использования результатов двух серий экспериментов . В первой серии для базового варианта (первого) σ max = σ m . Во второй серии σ max должны значительно превышать средние напряжения , что и достигалось для второго и третьего вариантов формы инденторов . Преобразуя формулу (1), получим

^max -° m = 3 ' к E Х

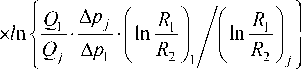
где величина

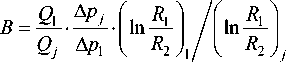
может быть названа общим коэффициентом подобия. Значение σm может быть определено как

E

СТ m = -, £

где £ - относительная деформация , которая в данном эксперименте может быть определена как

£ = I,

h

где h - толщина резиновой прокладки , h = 4 мм .

Тогда , используя экспериментальные значения перепадов давлений и соответствующих утечек из рис . 3-5 , а также принимая к = 0,05 , получим экспериментальное отношение o_max / o _m . Все результаты этих вычислений сведены в табл . 2 .

Зависимость экспериментального отношения o_max / o _m от внедрения индентора для вариантов 2 и 3 приведена на рис . 7 .

Q , мл/с

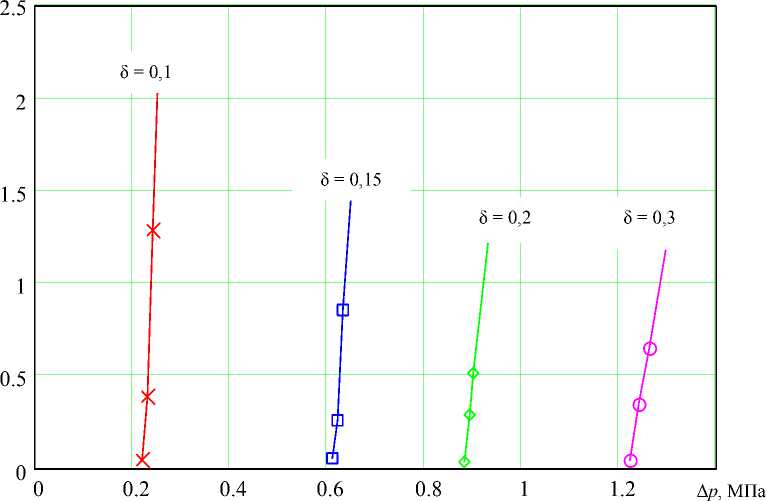
Рис. 3. Зависимость утечек от перепада давлений при различных внедрениях δ в резину индентора , изготовленного по варианту 1

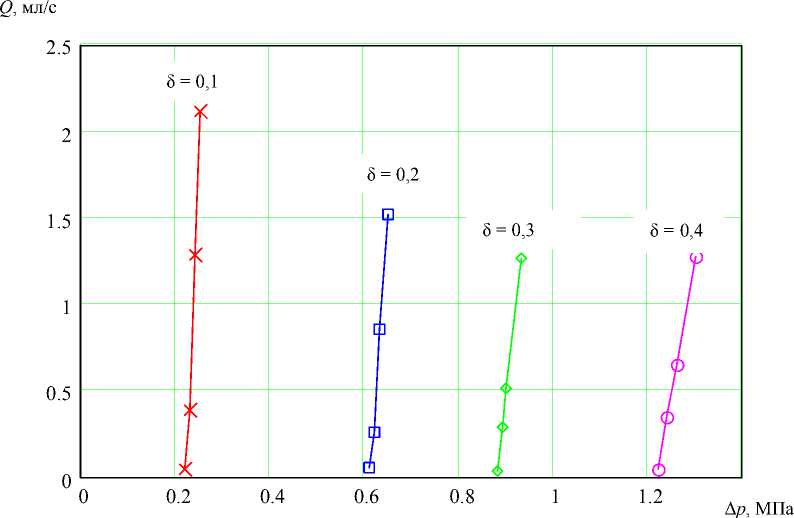
Рис. 4. Зависимость утечек от перепада давлений при различных внедрениях δ в резину индентора, изготовленного по варианту 2

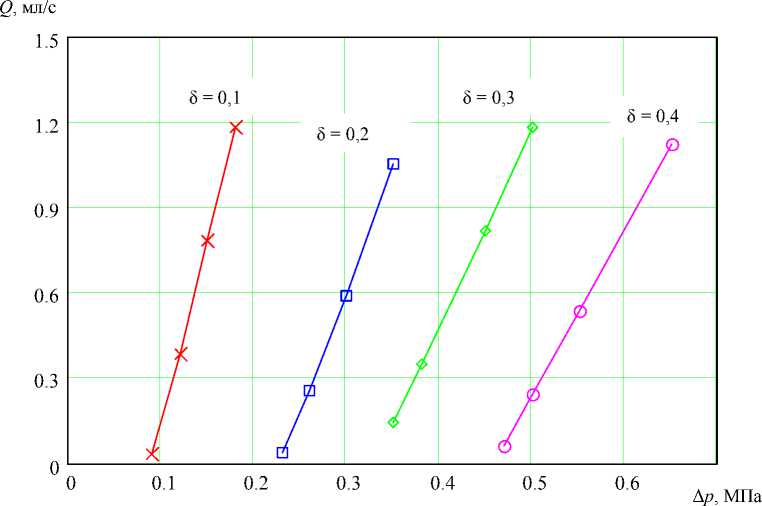
Рис. 5. Зависимость утечек от перепада давлений при различных внедрениях δ в резину индентора , изготовленного по варианту 3

Результаты вычислений геометрического коэффициента подобия

Таблица 1

5 , мм	R 1 , мм	R 2 , мм	R 1 / R 2	ln R 1 / R 2	f, R /f. R ln 1 ln 1 I   R 2 J,/ I   R 2 J V
1 вариант
0 , 1	13 , 72	12 , 08	1 , 1358	0 , 12646	1
0 , 2	13 , 77	12 , 03	1 , 1446	0 , 13506	1
0 , 3	13 , 80	12 , 00	1 , 1500	0 , 13977	1
0 , 4	13 , 80	12 , 00	1 , 1500	0 , 13977	1

Окончание табл. 1

5 , мм	R 1 , мм	R 2 , мм	R 1 / R 2	ln R 1/ R 2	f, R /f. R ln 1 ln 1 I   R 2 J,/ I   R 2 J j
2 вариант
0 , 1	13 , 20	12 , 60	1 , 0476	0 , 04650	2 , 72
0 , 2	13 , 30	12 , 50	1 , 0640	0 , 06204	2 , 17
0 , 3	13 , 50	12 , 30	1 , 0976	0 , 09313	1 , 50
0 , 4	13 , 60	12 , 20	1 , 1148	0 , 10868	1 , 29
3 вариант
0 , 1	13 , 06	12 , 74	1 , 0251	0 , 02479	5 , 10
0 , 2	13 , 10	12 , 70	1 , 0315	0 , 03101	4 , 37
0 , 3	13 , 10	12 , 70	1 , 0315	0 , 03101	4 , 50
0 , 4	13 , 10	12 , 70	1 , 0315	0 , 03101	4 , 50

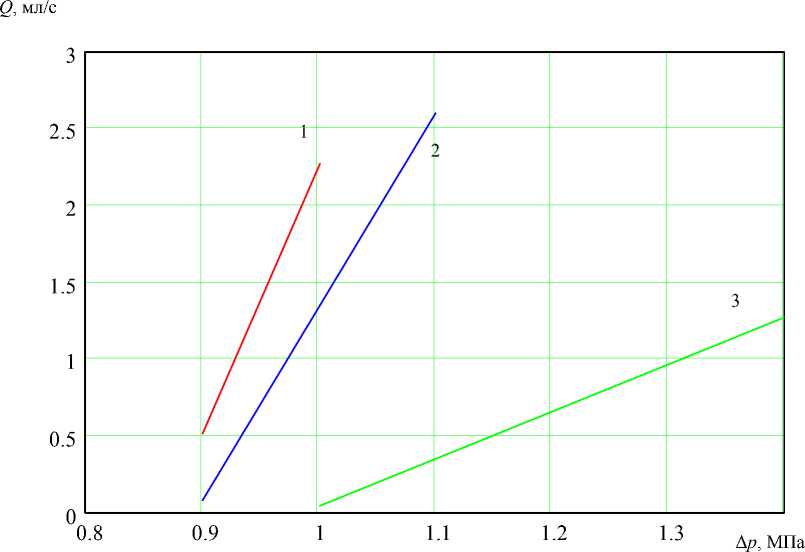
Рис. 6. Зависимость утечек от перепада давлений c учетом геометрического подобия при внедрении 5 = 0,2 в резину индентора , изготовленного по вариантам 1-3

Таблица 2

δ, мм	Q 1 , мл / с	Q j , мл / с	Δ p 1 , МПа	Δ p j , МПа	B	ε	σ m , МПа	σ max , МПа	^ max / G m
При сравнении второго варианта с базовым (первым)
0 , 1	1 , 280	0 , 640	0 , 24	0 , 18	4 , 08	0 , 025	0 , 08	0 , 155	1 , 93
0 , 2	1 , 260	0 , 540	0 , 93	0 , 44	2 , 40	0 , 050	0 , 16	0 , 207	1 , 29
0 , 3	1 , 270	0 , 724	1 , 30	0 , 88	1 , 78	0 , 075	0 , 24	0 , 271	1 , 13
При сравнении третьего варианта с базовым (первым)
0 , 1	1 , 280	0 , 780	0 , 24	0 , 15	5 , 10	0 , 025	0 , 08	0 , 168	2 , 10
0 , 2	1 , 260	0 , 588	0 , 93	0 , 30	4 , 37	0 , 050	0 , 16	0 , 218	1 , 36
0 , 3	1 , 270	0 , 820	1 , 30	0 , 45	4 , 50	0 , 075	0 , 24	0 , 287	1 , 20

Результаты вычислений экспериментального отношения a_max / a m

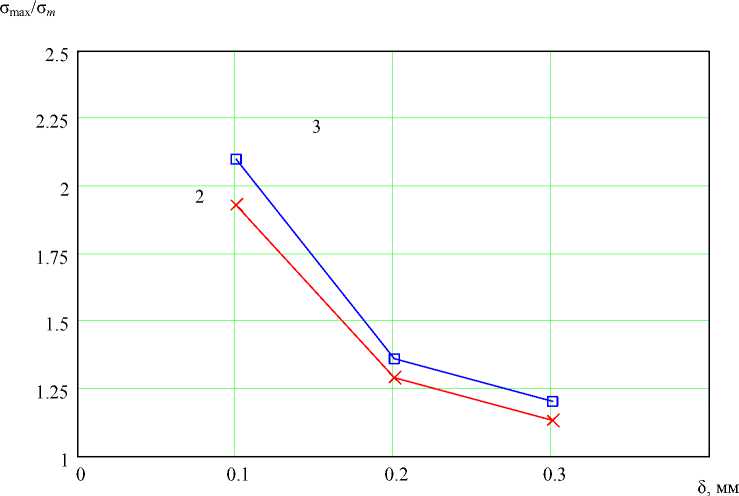
Рис. 7. Экспериментальная зависимость отношения a_max / a m от внедрения выступа , изготовленного по вариантам 2 и 3, в резину

Использование метода конечных элементов. Разработанные конечно-элементные модели трех используемых в эксперименте уплотнений с различными формами инденторов и использование программы STAR позволили теоретически изучить распределение напряжений по ширине площадки контакта . Эпюры нормальных напряжений по ширине площадки контакта для первого варианта индентора приведены на рис . 8 .

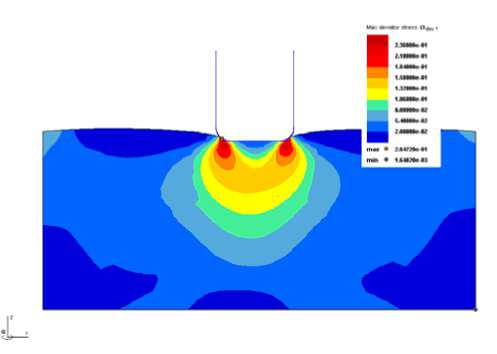
Рис. 8. Поля напряжений при внедрении индентора 1 в резину

Результатом этой экспериментально-теоретической работы явилось создание новой конечно-элементной программы для расчета утечек через неподвижные резиновые уплотнения LEAKAGES [14; 15], учитывающей форму резиновых прокладок, вязкоупругие свойства резины, а также явления релаксации и пол- зучести. Внешний вид окна программы LEAKAGES после расчета утечек для варианта 1 приведен на рис. 9.

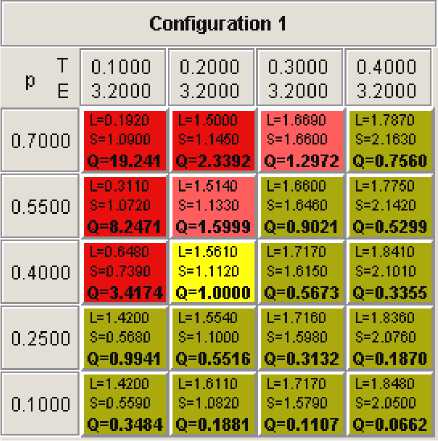
Рис. 9. Внешний вид окна программы STAR после расчета утечек для варианта 1

Заключение. Таким образом, в результате экспериментальных исследований по внедрению кольцевых инденторов различных профилей в резиновую неподвижную прокладку установлено, что за счет оптимизации формы индентора величина утечек может быть снижена в 10 раз. Разработана конечно-элементная программа для расчета утечек, которая позволяет оптимизировать форму вновь создаваемых резиновых уплотнений для ракетно-космической техники.