Влияние рассогласования импедансов в тракте передачи сигнала при калибровке задержек имитаторов навигационных сигналов

Введение. Для оценки точностных характеристик навигационной аппаратуры потребителей (НАП) – приемников сигналов спутниковых радионавигационных систем, а также специализированных приемников из состава наземного сегмента космического комплекса (НС КК) системы ГЛОНАСС, могут быть применены имитаторы навигационных сигналов (ИНС). Учитывая тенденции развития НАП, в частности угломерной и синхронизирующей, необходимо подтверждать погрешность измерения задержки НАП с субнаносекундным уровнем точности [1–3]. Требования к приёмникам из состава НС КК аналогичны: неисключённая систематическая погрешность измерения задержки не должна превышать долей наносекунд.

Необходимым условием для этого является наличие ИНС, калиброванного с лучшей точностью. Анализ доступных источников показал, что в настоящее время при прецизионной калибровке ИНС не оценивается и не учитывается влияние рассогласования импедансов в линии передачи высокочастотного навигационного сигнала [4–6]. Различие рассогласований входных импедансов аппаратуры, используемой для калибровки ИНС и НАП, тестируемой с использованием ИНС, может привести к появлению дополнительной систематической погрешности оценки точностных характеристик НАП. В связи с этим целью данной работы является определение величины погрешности оценки задержки, вызванной рассогласованием для определения её вклада в бюджет погрешности калибровки ИНС.

Математическая модель сигнала на входе устройства обработки сигналов с учетом рассогласования. На рис. 1 изображена схема калибровки ИНС (управляющая ЭВМ, стандарт частоты, кабельные сборки, необходимые для подключения вспомогательных элементов схемы, не показаны). В общем случае калибровка задержки ИНС заключается в том, что ИНС настраивается на формирование навигационного сигнала с заданной задержкой, устройство обработки сигналов (УОС) производит измерение задержки, и рассчитывается калибровочная поправка, соответствующая внутренней задержке сигнала в ИНС. При этом каждая имеющаяся в линии передачи навигационного сигнала электрическая неоднородность приводит к появлению дополнительного отраженного сигнала. На рис. 1 изображен только первый отраженный сигнал, попадающий на вход УОС и оказывающий наибольшее влияние на оценку задержки, так как он обладает наибольшей мощностью по сравнению с остальными.

Модель отраженного сигнала дополнительно упрощена за счет того, что рассматривается только сигнал, отраженный от высокочастотных разъемов УОС и ИНС, и не рассматриваются сигналы, вызванные рассогласованиями внутри ВЧ-кабеля, ИНС, УОС и переходов. Тогда, если принять, что ВЧ-кабель не вносит никаких искажений в сигнал (АЧХ постоянна и ФЧХ линейна в полосе частот сигнала), справедлива следующая модель сигнала на нулевой частоте на входе алгоритма обработки, реализованного в УОС:

s УОС ⁽ t ) = s ИНС ⁽ t - t каб ) + | Г| ■ s ИНС ⁽ t - ³ ' t каб ) ^X

X exp ( j ■ [ ф г - 2 ■Л^ f о ■ 3 ■ t _К а _б ] ) , (Г)

где s _УОС – сигнал на входе УОС; s _ИНС – сигнал на выходе ИНС; t _каб – задержка на распространение сигнала в кабеле; Г – произведение модулей коэффициентов отражения (КО) ИНС и УОС; φ Г – сумма фаз КО ИНС и УОС; f ₀ – несущая частота сигнала.

Анализ работы алгоритма корреляционной обработки для принятой модели отраженного сигнала. Оптимальным методом при оценке задержки сигнала в присутствии белого гауссовского шума с точки зрения минимума среднего квадрата погрешности оценки является корреляционный метод [7–9]. Оценка задержки корреляционным методом соответствует моменту времени, при котором модуль огибающей взаимокорреляционной функции входного и опорного сигналов максимален.

Рис. 1. Появление отраженного сигнала при калибровке ИНС

Fig. 1. Аppearance of a reflected signal during ANN calibration

В силу линейности алгоритма корреляционной обработки модели сигнала (1) соответствует комплексная огибающая сигнала на выходе коррелятора:

K, (t) = K o( t) + |P| ■ Ko( t -At) X xexP(j[фг -2-л-fo -At]),              (2)

где K ₀ ( t ) – автокорреляционная функция сигнала на выходе ИНС; K ^ ( t ) - взаимная корреляционная функция между сигналом на выходе ИНС и сигналом на входе УОС; A t = 2 ■ t _каб - задержка отраженного сигнала по отношению ко времени прихода прямого сигнала (дополнительная задержка).

Модуль корреляционной функции (2) для значений Г <<  1 приблизительно равен

| K, (t )| = |K о( t )| + |Г| x xKо(t-At)|■ cos(фГ -2■л^ f) ■At).         (3)

Выражение (3) получено в предположении, что фаза комплексной автокорреляционной функции сигнала на выходе ИНС постоянна на интервале от момента прихода прямого сигнала до прихода отраженного сигнала, т. е. arg ( K ₀( t ) ) = arg ( K ₀ ( t - A t ) ) .

Погрешность оценки задержки как разность положений максимумов функций K ₀( t ) и K ^ ( t ) может быть получена в результате решения следующего уравнения относительно ст _t :

''

IK0 (t0 + стt )| + 1Г1 ■ IK0 (t0 -At + стt )| x xcos(фГ -2■л^ f) ■At) = 0,              (4)

где t ₀ – момент, соответствующий максимуму корреляционной функции; ст _t - погрешность оценки задержки корреляционным методом.

При небольших значениях ст _t решение (4) имеет следующий вид:

K 0 ( A t )|'       ,                     .

^ст t =^- |Г| ■            ■ cos ( ф р ^- 2 -л- f 0 -^A t ) .

K 0 (0)

Для получения решения уравнения (4) в аналитическом виде необходимо аппроксимировать функцию K ₀ ( t ) в районе основного максимума некоторой аналитической функцией. Ниже приведены решения при аппроксимации функции K ₀ ( t ) параболой и гаус-соидой:

ст t =-|Г| ■A t ■ cos ( ф р - 2 'Л' f 0 ■A t ) ,         (5)

^ст t

|P|■A t ■ cos ( ф _р - 2 ■л^ f 0 ■A t )

exp |— 2 | + |P|■ cos ( ф _г - 2 ■л^ f 0 ■A t )

где c – коэффициент, пропорциональный длительности чипа дальномерного кода сигнала на выходе ИНС.

На рис. 2 приведены зависимости погрешности оценки задержки, полученные для сигнала ГЛОНАСС L3OС [10] (тактовая частота 10,23 МГц, |Г| = 0,01,

φ Г рассчитывается для каждого значения дополнительной задержки из условия, что прямой и отраженный сигналы синфазны).

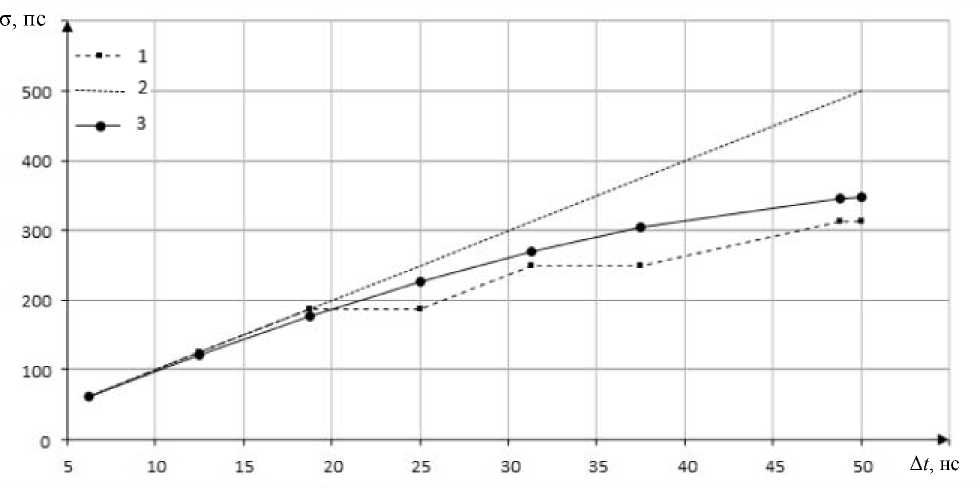
Рис. 2. Погрешности оценки задержки: 1 – значение погрешности, определенное по результатам имитационного моделирования в среде MatLAB для заданных условий работы; 2 – значение, вычисленное по (5); 3 – значение, вычисленное по (6) при с = 83 нс

Fig. 2. Delay evaluation errors: 1 is the error value determined from the simulation results in the MatLAB environment for the specified operating conditions, 2 is the value calculated from (5), 3 is the value calculated from (6) at c = 83 ns

Характеристики измерительных устройств, связанные со значением КО

Устройство	Характеристика и ее значение	Значение КО
ИНС Spirent GSS 9000 [12]	КСВН ВЧ-выхода 1,2	0,09 (–20,8 дБ)
ИНС Aeroflex Avionics GPSG-1000 [13]	КСВН ВЧ-выхода 1,3	0,13 (–17,7 дБ)
Цифровой осциллограф Agilent DSO9404a [14]	Входное сопротивление 50 Ом ± 2,5 %	0,0123 (–38,2 дБ)
Цифровой осциллограф Rohde&Schwarz RTO1044 [15]	Входное сопротивление 50 Ом ± 1,5 %	0,0074 (–42,6 дБ)

Анализ рис. 2 приводит к выводу, что выражения (5) и (6) достаточно точно описывают погрешность, полученную по результатам моделирования при значениях Δ t менее 50 нс (что соответствует длине измерительного кабеля 5,76 м при коэффициенте укорочения волны 1,3).

При этом погрешность, полученная по (6), является более близкой к результатам моделирования (разность фактического значения и расчетного не превышает 60 пс). Это связано в первую очередь с тем, что выражение (6) учитывает спектральные характеристики сигнала (параметр c ). Выражение (5) является более универсальным и менее точным (разность пропорциональна |Г| и ∆ t и не превышает 200 пс).

Как следует из (4), погрешность (5) и (6) напрямую зависит от погрешности аппроксимации первой производной I K 0 ( t ) I , которая определяется видом и значениями параметров аппроксимирующей функции, а также интервалом аппроксимации. Чтобы получить наиболее точное выражение для расчета погрешности, вызванной рассогласованием при различных значениях дополнительной задержки, необходимо выбирать интервал аппроксимации производной модуля автокорреляционной функции сигнала на выходе ИНС, соответствующий диапазону изменения дополнительной задержки отраженного сигнала, имеющему место при калибровке ИНС. Этот диапазон необходимо выбирать, исходя из следующих фактов:

• 1)    длина измерительного кабеля обычно составляет единицы метров (1–5 м);

• 2)    скорость распространения сигнала в кабеле меньше скорости света на 15–30 %.

Учитывая эти факты, диапазон значений дополнительной задержки целесообразно задать от 8 до 50 нс. При этом для расчета погрешности можно использовать выражение (5).

Количественная оценка значения погрешности. Для количественной оценки исследуемой погрешности необходимо задать диапазон возможных значений параметров отражения. Источником этих данных могут служить технические характеристики ИНС и УОС. Следует отметить, что для точных оценок параметров сигналов ИНС обычно используются анализаторы навигационных сигналов, представляющие собой совокупность цифрового осциллографа и специального программного обеспечения [11]. В таблице приведены технические характеристики приборов, определяющие значения |Г|.

Анализ данных, представленных в таблице, позволяет сделать вывод, что значение |Г|, т. е. произведения модулей КО ИНС и УОС, может достигать значений от 0,00067 до 0,0016 при значении импеданса разъе- мов кабеля 50 Ом. Поскольку импеданс разъемов кабелей отличается от номинального значения (КСВ до 1,15 для прецизионных соединителей), диапазон значений |Г| будет составлять от 0,012 до 0,017.

Подстановка имеющихся значений параметров отражения в (5) позволяет заключить, что значение систематической погрешности кодовой оценки задержки НС, вызванной отраженным сигналом при калибровке ИНС, может достигать 100–150 пс для кабеля длиной 1 м и 600–750 пс для кабеля длиной 5 м (без учета потерь в кабеле) для различных сигналов, значений несущей частоты и параметров отражения.

Заключение. В данной статье был проведен анализ влияния рассогласования импедансов в линии передачи высокочастотного сигнала при калибровке ИНС. В результате анализа получена модель сигнала на входе алгоритма обработки и определены предельные значения систематической погрешности измерения задержки. Учитывая, что калибровка ИНС должна проводиться с субнаносекундным уровнем точности, необходимо учитывать влияние рассогласования. Самый простой способ учета – измерение значений параметров отражения, например, рефлектометрами или векторными анализаторами цепей с последующим вычетом рассчитанных значений погрешности из измеренных УОС задержек. Получены выражения для расчета значения погрешности по известным параметрам отражения. Для сигнала ГЛОНАСС L3OC расчетные значения отличаются от истинного не более чем на 60 и 200 пс (для выражении (5) и (6) соответственно). Поскольку данный сигнал является сигналом ГЛОНАСС с наиболее широким спектром, можно предположить, что для других сигналов погрешность будет ещё меньше.