Влияние разности коэффициентов сопротивления качению ведущих колес на устойчивость автомобиля против заноса

При качении колеса с эластичной шиной по дороге с твердым покрытием вес автомобиля, приходящийся на колесо, деформирует шину и опорную поверхность. В передней половине пятна контакта происходит радиальное сжатие шины, сопровождаемое уменьшением радиуса от свободного до динамического, а в задней половине контакта - уменьшение сжатия, сопровождаемое увеличением радиуса от динамического до свободного. В результате внутреннего трения в шине и относительно небольшого трения между шиной и дорогой изменяется эпюра элементарных нормальных реакций и смещается результирующая сила от оси вращения колеса на величину плеча сопротивления качению. При этом вертикальная реакция создает относительно центра вращения колеса момент сопротивления качению. Момент сопротивления качению оказывает влияние на устойчивость и управляемость автомобиля в результате несимметричности касательных реакций, действующих на его колеса. Несимметричность касательных реакций возможна, например, при различных нормальных нагрузках на правое и левое колеса каждой из осей автомобиля. В результате несимметричности касательных реакций создается момент, стремящийся повернуть автомобиль относительно оси, перпендикулярной к плоскости движения.

При действии боковых сил (поворот автомобиля, поперечный уклон дороги, боковой ветер, движение по неровной опорной поверхности)

коэффициент сопротивления качению может значительно возрасти в результате боковых деформаций шин. С увеличением передаваемого через колесо крутящего момента указанный коэффициент увеличивается как в результате большей тангенциальной деформации, так и в результате увеличения работы трения в контакте шины с опорной поверхностью.

АНАЛИЗ ПОСЛЕДНИХ ДОСТИЖЕНИЙ

И ПУБЛИКАЦИЙ

Фундаментальным исследованиям сопротивления качению посвящены работы Е. А. Чудакова [10], В. И. Кнороза [5], Г. А. Смирнова [9], А. С. Шелухина [11], А. Н. Туренко [2] и других ученых. За рубежом также опубликовано большое число трудов по этому вопросу.

В работе [6] отмечается, что на величину коэффициента сопротивления качению в общем случае оказывают влияние следующие факторы:

• •    конструктивные: диаметр шины, ширина профиля шины, толщина профиля шины, рисунок протектора, число слоев корда, конструкция каркаса, величина передаваемого через шину момента;

• •    технологические: используемые материалы, технология изготовления шин;

• •    эксплуатационные: тип и состояние дороги, скорость движения, вес, приходящийся на колесо.

С увеличением скорости движения колеса коэффициент сопротивления качению, как правило, возрастает. Начиная с 80-90 км/ч даже на ровных дорогах указанный коэффициент начи- нает быстро увеличиваться [1]. Оптимизация конструкции шины, улучшающая ее энергетические свойства, позволяет снизить сопротивление качению колес в 2-3 раза [4].

А. С. Литвиновым совместно с Я. Е. Фароби-ным [7] был поставлен эксперимент по определению моментов сопротивления качению шины 6,00-16 при углах увода, изменяющихся в пределах 0-14° при различных нормальных нагрузках и разных давлениях воздуха в шине.

Определено, что при движении автомобиля по дороге с твердым покрытием коэффициент сопротивления качению увеличивается с уменьшением давления воздуха в шине. При передаче крутящего момента коэффициент немного возрастает, так как шина в этом случае деформируется не только в вертикальном направлении, но и по окружности. При большом передаваемом крутящем моменте элементы протектора проскальзывают по дороге и на трение в области контакта затрачивается дополнительная энергия.

Трение в дифференциале рассмотрено в работе А. С. Литвинова [6]. Однако в указанной работе не рассмотрено влияние разности коэффициентов сопротивления качению на ведущих колесах на величину дополнительных составляющих боковых сил, действующих на переднюю и заднюю оси автомобиля. В работе [3] приведены результаты экспериментальных исследований грузовых автомобилей МАЗ и Урал с серийными (коническими) дифференциалами и дифференциалами свободного хода и повышенного трения. Определено, что при установке дифференциалов повышенного трения значительно снижается курсовая устойчивость автомобиля. Однако в этих исследованиях не определены условия возникновения заноса автомобиля при бортовой неравномерности коэффициентов сопротивления качению ведущих колес и различных значениях коэффициента блокировки дифференциала.

ЦЕЛЬ И ПОСТАНОВКА ЗАДАЧ ИССЛЕДОВАНИЯ

Целью исследования является определение условий устойчивого движения автомобиля при бортовой неравномерности коэффициентов сопротивления качению ведущих колес. Для достижения указанной цели необходимо решить следующие задачи:

• •    исследовать динамику ведущего моста автомобиля;

• •    оценить устойчивость автомобилей различной компоновки при разности коэффициентов сопротивления качению ведущих колес различных бортов.

ДИНАМИКА ВЕДУЩЕГО МОСТА АВТОМОБИЛЯ

На рис. 1 приведена схема сил, моментов и реакций, действующих на ведущее колесо автомобиля.

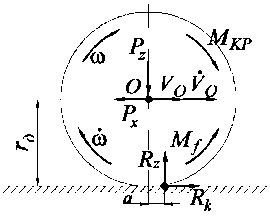
Рис. 1. Схема сил, действующих на ведущее колесо автомобиля: P Z - вертикальная сила, действующая на колесо;

R z - нормальная реакция, действующая на колесо;

R k - горизонтальная реакция дороги на колесо;

М к - крутящий (вращающий) момент на колесе; P x -горизонтальная реакция на оси колеса; го и ГО - угловые скорость и ускорение колеса; V_o и V_o - линейные скорость и ускорение колеса; г д - динамический радиус колеса; M f - момент сопротивления качению; а - плечо трения (коэффициент трения качения)

У ведущего колеса крутящий (вращающий) момент М _к превосходит момент сопротивления качению, который определяется зависимостью

M f = a - R z .                        (1)

Тангенциальная (касательная) реакция на колесе R k имеет положительное направление, то есть совпадает по направлению с вектором скорости V. Момент сопротивления воздуха вращению колеса и сила сопротивления воздуха его поступательному перемещению весьма малы, и ими обычно пренебрегают.

Касательная реакция на колесе

R k = М КР - а - R Z = Р окр - f . R z ,        (2)

rd где Рок - окружная сила на колесе, f- коэффициент сопротивления качению.

f = —.                     (3)

r д

Занос автомобиля может возникнуть вследс- твие появления поворачивающего момента, обусловленного неравномерностью касательных реакций на ведущих колесах противоположных бортов машины [8]. Одной из причин появления бортовой неравномерности касательных реакций является изменение коэффициента сопротивления качению (рис. 2).

f ’ = 0,007-0,015

/Сухая укатанная грунтовая дорога

<Асфальтобетонная дорога в хорошем состоянии f ' = 0,025-0,030

Рис. 2. Участок окружной дороги г. Харькова с различными значениями коэффициента сопротивления качению f и f"

На рис. 3 приведена схема сил, действующих на заднеприводный автомобиль при разности коэффициентов сопротивления качению веду-

R = —- f '• R'z = 0,5-(ф + f')• Rz - rд

- 0,5 • f ' ■ R_z = 0,5 • ф- R_z ;                   (8)

щих колес.

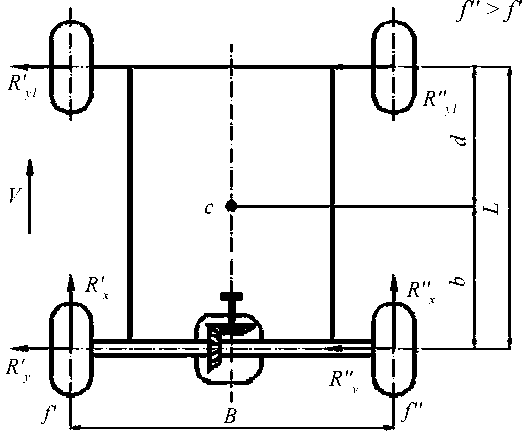
Рис. 3. Схема сил, действующих на заднеприводный автомобиль при разности коэффициентов сопротивления качению ведущих колес:

V - линейная скорость автомобиля; f’ и f" - коэффициенты сопротивления качению левого и правого колес, f" >  f’;

R’_y , R" - боковые реакции на левом и правом колесах задней оси; b , d - координаты проекции центра масс автомобиля с на горизонтальную плоскость; R’_y/ , R"_y1 -боковые реакции на левом и правом колесах передней оси;

B , L - колея и продольная колесная база автомобиля; R’ , R"_x - касательные реакции на левом и правом колесах

M"

R x =     - f "• R z = 0,5 -( ф + f ") • R z • 7 -0,5• f''• R z . (9)

rд

Поворачивающий момент, возникающий на оси автомобиля,

^Mпо. = ^{B -( R -} R X ) .               (10)

Боковая сила, которую способна воспринимать ось автомобиля без бокового скольжения:

R y = r ; + r ; = r ; = 7 ф ² • R z ² - R x² . a d

Величина R' = 0, поскольку на забегающем колесе мы допустили равенство касательной реакции предельной силе по сцеплению. Учитывая, что R' z = 0,5 • R z , и подставляя (9) в (11), получим после преобразований:

R y = 0,5 • ф - R z • 1

—

7 fA

1 + f- • 7

7 ф J

бл

—

г

ф

. (12)

После подстановки (8) и (9) в (10) получим:

M пов = B - ( ф + f ') • R z '(.„ - 1 ) .             (1 ³ )

Выражение под корнем в уравнении (12) боль-

ше нуля при

Появление разности указанных коэффициентов приводит к перераспределению касательных реакций на колесах, при этом мост стремится развернуться вокруг колеса, у которого большее сопротивление качению. Следовательно, колесо, имеющее меньшую величину коэффициента сопротивления качению, является забегающим, а большую - отстающим.

Предположим, что на забегающем колесе реализована предельная касательная реакция, равная предельной силе сцепления. В этом случае крутящий момент на забегающем колесе M к, = ( ф + f ') • R' z' Г д = 0,5 Аф + f ') • R z • Г д .        (4)

Крутящий момент на отстающем колесе

M к, = MА •      = 0,5 Аф + f ) • R z ■ Гд ^х

K

1 - K х ,.,    0,5-(Ф + f )- Rz • rd • 7,             (5)

K

f"

^бл <  ф + f"’

поскольку в противном случае ось автомобиля неспособна воспринимать боковую силу. Это означает, что боковая устойчивость оси обеспечивается при R" x < R' x и М нов <  0 (см. зависимость (10)). Поэтому выражение (13) следует преобразовать к виду

M .о. = B • ( R' x - R x ) = 4 Аф + f • У Rz-. ■ (1 - 7 ., ) . (15)

где К' - доля крутящего момента, приходящаяся на забегающее колесо,

K* =

M ’ кр

M' + M" ’ кр кр

X б - коэффициент блокировки дифференциала, ”          7 =       .                      (7)

Касательные реакции на ведущих колесах:

УСТОЙЧИВОСТЬ АВТОМОБИЛЯ

ПРИ РАЗНОСТИ КОЭФФИЦИЕНТОВ СОПРОТИВЛЕНИЯ КАЧЕНИЮ

ВЕДУЩИХ КОЛЕС РАЗЛИЧНЫХ БОРТОВ

Коэффициент устойчивости автомобиля

	[ R y 2 • L	-    для заднеприводного автомобиля; -    для переднеприводного автомобиля; -    для полноприводного автомобиля,
K = М стб =, уст М пов	М по. 2 R y 2 • L		(16)
	М по. Ry • L y 2		(17)
	M +M пов 1          по. 2		(18)
где М б - стабилизирующий момент, СТ     Mстб = Ry 2 • L ,			(19)

R ₂ - максимальная возможная боковая реакция дороги на задней оси автомобиля; М п_ов1 , М п_ов2 -поворачивающие моменты на передней и задней ведущих осях соответственно,

M пов 1 = B - ( ф + f ’) ■ R z i - ( 1 - ч) (20)

M ПО. 2 = B Ч ? + f ') • R 2 - ( 1 - ^,. 2 )■ ⁽²¹⁾

Очевидно, что условие устойчивости будет обеспечено при К ст > 1. Условие отсутствия бокового увода за счет бокового скольжения передней оси под действием поворачивающего момента

Графики зависимостей К с (^ бл) при различных значениях f ' для автомобилей каждого из указанных типов приведены на рис. 4, 5, 6. Устойчивость автомобиля против заноса обес-

М

пов ₂

Rv ■L ^1

y ₁

М пов 1

• -    для заднеприводного автомобиля;

• -    для переднеприводного автомобиля;

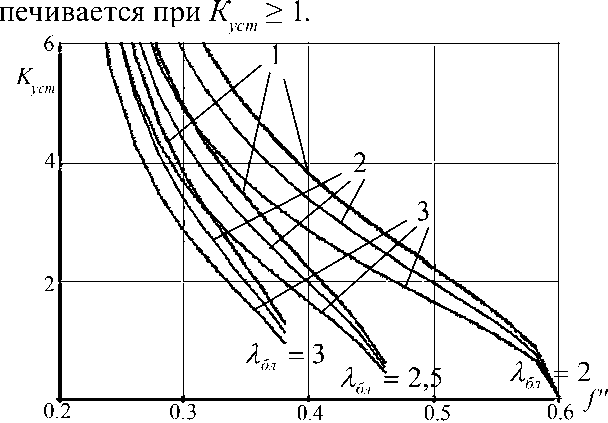
Рис. 4. Зависимость К ст = К ст ( /" ) для заднеприводного автомобиля при различных значениях L IB:

1 - L IB = 1,9 (BMW 318i); 2 - LIB = 1,68 (VW 1600);

3 - LIB = 1,41 (MCC Smart)

М + М - для полнопривод- .    ^пов 1        ^пов 2 ного автомобиля,

где R 1 - максимально возможная боковая реакция дороги на передней оси автомобиля.

Максимально возможные боковые реакции дороги на осях автомобиля:

2 - для задне-иполнопри- (25) водного автомобиля;

0,5 ■ ф- Rz,

■

—

1 +

ф

—

f"

ф

ф- R _z   - для переднеприводного автомобиля,

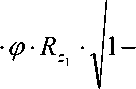
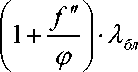
ф

2 - для задне-и полноприводного автомобиля;

ф ■ R z   - для заднеприводного автомобиля.

В выражениях (25)-(28) параметры с индексом «1» относятся к передней оси автомобиля, с индексом «2» - к задней оси. При равномерном движении, пренебрегая влиянием аэродинамической силы, получим:

R„ = m - g ■ у ,                     (29)

R z 2 = m ^- g ■ L ,                      (30)

где m - общая масса автомобиля.

Подставляя выражения (20), (21), (25)-(30) в уравнения (16), (17), (18), получим после преобразований:

L J 1 - [(1+ Вх - £] 2

2 — ³----- 7 ^------ — - для заднепривод- (31)

B (1 ₊ 2 _). (1 - х )     ного автомобиля;

- л

Ф" %

K = <  4___ bo _____- для переднепривод- (32)

уст B ( ф + f ") ■ (1 - Х _бл ) ного автомобиля;

1 - [(1 + f¹   - £] ²

ϕϕ

------тт;-------------- привод на все z,-,^ (1 + f -) ■ (1 - Я _б )    колеса.           ⁽³³⁾

ϕ

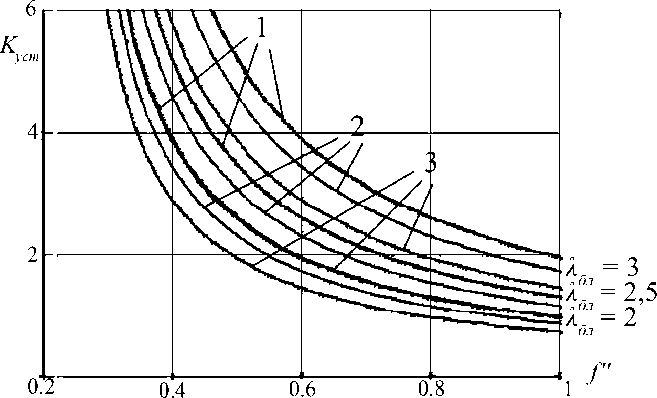
Рис. 5. Зависимость К_{ус т} = К _уст ( f" ) для переднеприводного автомобиля при различных значениях параметра Ф = — • —:

1 - Ф = 2,03 (ALFA Romeo 166); 2 - Ф = 1,91 (SEAT Toledo 1,8);

3 - Ф = 1,8 (ВАЗ-2110)

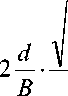
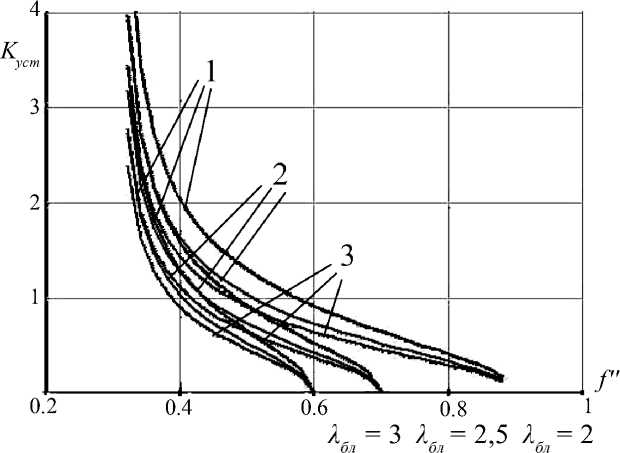
Рис. 6. Зависимость К = К (f" ) для полноприводного автомобиля при различных зпалениях d I В : 1 - d I В = 1,0 (FORD Explorer); 2 - d IВ = 0,8 (ВАЗ-21213);

3 - d IВ = 0,7 (AUDI A6 1,8 Quattro)

ВЫВОДЫ

• 1.    Полученные зависимости позволяют оценить устойчивость автомобиля против заноса и бокового увода при наличии бортовой неравномерности коэффициентов сопротивления качению левых и правых ведущих колес.

• 2.    Снижение коэффициента сцепления колес с дорогой увеличивает опасность заноса при существовании разности коэффициентов сопротивления качению ведущих колес.

• 3.    При попадании одного из ведущих колес заднеприводного автомобиля на участок дороги с коэффициентом f > 0,35 (рыхлый снег, грунтовая дорога в период распутицы, бездорожье) возможно снижение К ст меньше единицы. Для полноприводных автомобилей К <  1 при попадании на участок с f > 0,4 (заболоченная местность). Переднеприводные автомобили более устойчивы против заноса в тяговом режиме движения, чем полно- и заднеприводные.