Влияние развития пластических деформаций в компонентах на макроскопическое упрочнение упругопластических композитов

Mode! of deformations of two components composite material with elastic - plastic inclusions and elastic matrix is constructed, according io which the plastic current begins not simultaneously in all points of inclusions, and in their separate areas. Effective parameters of the nonlinear constitutive relations of composite material at limit of elasticity are calculated and is shown, that at distribution of plastic current on whole volume of inclusions this law becomes the law linear kinematic of hardening.

В работе [1] построена модель деформирования двухкомпонентного композиционного материала с упругопластическими включениями и упругой матрицей, согласно которой пластическое течение начинается одновременно во всех точках включений. В публикуемой работе предлагается модель, учитывающая возникновение зон пластического течения в отдельных областях включений и их распространение на весь объем включений.

Пусть двухкомпонентный композиционный материал занимает объем V , ограниченный поверхностью 5.

Первый компонент композита образует идеально упругую связующую матрицу Vj

° У ~ “ Ml -у "*" ^у ^1 hqq 1

а второй компонент Vf представляет включения сферической формы

собой отдельные упругопластические

Оу ^ М2 у^'у " ^ец j "*" ^у ^j 6^

Здесь сту, £у — компоненты тензоров локальных напряжений и полных деформаций, еу —компоненты тензора пластических деформаций, p_s, Я, — параметры Ламе изотропных компонентов, пластические деформации удовлетворяют условию несжимаемости: е^Р_ч=0.

Пластические свойства материала включений задаются поверхностью текучести Мизеса с соответствующим ассоциированным законом течения:

- ^2 , ^sy - ^2

е*р

Г*р *р \ек! ек1

Здесь у_у =а_1} - -буо^ , е_ц = г:,, --^ е_ад , к₂ — предел текучести включении, (точкой обозначены скорости пластических деформаций).

Геометрическая структура такого двухкомпонентного композиционного ма териала описывается случайной изотропной функцией координат к₂ (г). равной единице в объеме С, и нулю вне этого объема. Кроме того геометрические особенности возникающих и развивающихся в объеме включений зон пластического течения V_p описывает дополнительная индикаторная функция к,,!^. равная единице с объеме V_р ^0p7₂j и нулю вне этого объема.

С помощью этих функций локальный закон Гука для среды записывается в виде сту (г) = 2 ц, еу (r^ + Sy Л, е„ (г) +

Цф'Ь?О') ^{+ 5}ч P]^£w(^r)) ^к2^- ²/С ^,у (*')*"/>(')•

Индикаторные функции, напряжения, полные и пластические деформации предполагаются статистически однородными и эргодическими случайными полями, поэтому их математические ожидания заменяются средними значениями по полному объему V , объемам компонентов V_s (s—L 2) и объему У_р [2]:

(// = “ J Д' №. (Д,р - ~~ j /(Г№ I                           s.p у где угловыми скобками обозначена операция осреднения.

Для определения макроскопического поведения рассматриваемого композиционного материала и вычисления его эффективных характеристик локальные уравнения (1) . (2) необходимо осреднить по объемам Ри К_р:

/    \   .2.3 Ц р\[    р\\1 2

\ ^ij ^ij / — к2 , 4 ц2 Ц^у — Су I1 Су — Су I у — к2 . Р            о

^Ч ) = ² Ml V" V ? ^{+ 5}Ч ^Х1 Vw/ ⁺_с2 1² L^ I \^ЕМ ) ₂⁺ ^ Р1 Ч'ЧЧ К)^{1 Ц1 С}Р\^е^И _р^{Л 3 J}

Соотношения (3) показывают, что для установления эффективного закона

Vеч)2' ^ihр

Гука необходимо выразить величины

\еу > через макроскопические '' р деформации (Ду^ и остаточные деформации ву . которые измеряются в композиционном материале после снятия внешних нагрузок. Это достигается статистическим осреднением системы деформирования среды, состоящей из уравнений (?.). уравнений равновесия • cil414V^^O

и соотношений Коши

2‘-,.Дг)=ц!>7. (г) + ьо,(г) .

связывающих компоненты тензора деформаций с компонентами вектора перемещений и,(г). Граничными условиями для замкнутой системы (1). (4). (5) являются условия отсутствия флуктуаций величин на поверхности S объема V :

H-'U-AfY

Следуя работе [3]. будем пренебрегать флуктуациями полных и пластических деформаций в объемах У2 и Vp. Тогда уравнение (1) принимает вид о",у (г) = 2Р1 Еу (г) + 5у X, Е^^ +

+(2W(^)2 +^ui^w)J ^w-2 ^«у^ p(r).

Здесь [/] = /;-// •

С помощью тензора Грина

G*( = 5ik ГЧЧ ~ 1 r,ik ’ Г = И ■ ВлР]\   44 Л] +8Р] ’ / система уравнений (7), (4), (5) с граничными условиями (6) может быть сведена к системе интегральных уравнений вида [I]

Су (^г) = j ^Gik,jiV ~ ^riVki ^A^dri •                                          (8)

Здесь

Определим сначала эффективный закон Гука рассматриваемого композиционного материала и его остаточные макроскопические деформации. Подставляя уравнение (8) с выражением (9) для Ту в известное соотношение [1]

\£ijY=\£ij/,'Cs \Ks £Ч )                                                    (1(1)

и используя свойство изотропности функций к'2(г^, кДг). находим уравнения относительно величин

¹ , решая которые получаем р

/ т^си / р\ ) с2 СР\е<Ир)

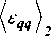
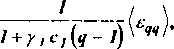
(Н)

Р 1 + ajCjVm -i)V л v р' ' J' р)

Здесь

/ 4-5 v,

15 L-v,

1 / + Vj           Aj

3 1- V/ ’ ^V* "  2U) н

Подставляя формулы (11) в соотношение объемную части, находим

ц. К,          2

= Л, + -/.-,

Hi                   3

(3) и выделяя девиаторную и

\^S‘j^^-^H (\^eV? ^ev) ’ (°w) ^^ (^fw)‘                            ^~*

Здесь

,    ( сЛт-1) \   *    ( c2(q-A

/ = д,\1+-—^M   '   , к* = к i+— О-³)

A 1+а^‘^т- l)j      Д   1 + пеДд-1),

— эффективные модули сдвига и объемного растяжения (сжатия). Остаточные деформаниии ву связаны с макроскопическими пластическими деформациями соотношением

Н / = ~ (^{7 +} (“/ ^ + ^с2^ " ⁷))4-                                 <¹⁴>

Для определения макроскопического поведения композиционного материала за пределом упругости необходимо осреднить соотношения (1) по объему зоны пластического течения Г_р . Применение к первому из соотношений (3) допущения об отсутствии флуктуаций величин в объемах У₂ и У_р и правила механического смешивания дает

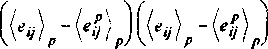
^1

*Н22

уравнения (15) с помощью формул (11)-(14) деформации

Исключая из

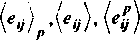
. находим закон нагружения рассматриваемой среды

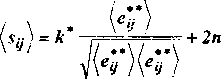
Здесь

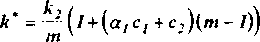
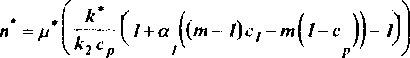
- эффективный предел текучести и коэффициент упрочнения соответственно.

Уравнения (16) описывают нелинейное деформирование композиционного материала за пределом упругости.

Эффективный предел текучести к характеризует начальную поверхность текучести. Он является линейной функцией концентрации и при с2 = 1 равен пределу текучести материала включений к2. Коэффициент упрочнения л*задает скорость перемещения и деформирования цилиндра Мизеса в шестимерном пространстве напряжений. При ср = с2 (что соответствует наличию пластического течения в каждой точке включений) формула для п* совпадает с аналогичной формулой работы [1].

Ьиблисграфическчй список