Влияние ряда коридорного пучка на теплообмен в пульсационном потоке

Теплообменное оборудование оказывают влияние на технико-экономические показатели промышленных установок и в частности на показатели установок топливно-энергетического комплекса (ТЭК). Масса теплообменного оборудования в составе ТЭК составляет львиную долю от массы установок в целом. От эффективности процессов теплообмена зависят показатели установок ТЭК в целом. Поэтому даже незначительное повышение эффективности процессов теплообмена может привести к значительному энерго- и ресурсосбережению. Повышение энергоресурсоэффективно-сти теплообменных аппаратов тесно связано с исследованиями современных методов интенсификации теплообмена. Одним из таких методов является пульсация потока, которая создается искусственно с целью интенсификации теплообмена [1, 2].

Теплообмен и гидродинамика пучков труб является классической задачей многие десятилетия. Внешний теплообмен в пучках труб достаточно хорошо изучен при стационарном течении. В работе [3] на основе проведенных экспериментальных исследований приведены обобщающие зависимости для расчёта теплоотдачи в зависимости от числа Рейнольдса Re в диапазоне от 1 до 2 · 105 и числа Прандтля от 0,7 до 1000. Теплообмен в пучке труб обусловлен геометрическими и режимными параметрами, при этом различия в конфигурации пучков труб, встречающихся на практике, совместно с режимами течениями заставляют авторов продолжать исследования в этой области [4, 5].

С развитием вычислительных мощностей и средств численных методов расширилась возможность более детального изучения течения в пучках труб. Течение в пучках труб зачастую имеет нестационарную природу течения, характеризующуюся переменным вихреобразованием в следе цилиндров. Нестационарность в пучках труб возникает произ- вольно в зависимости от геометрических и режимных параметров [6]. Нестационарность может создаваться искусственно, например, для интенсификации теплообмена. Такие течения зачастую называют пульсирующими течениями или осциллирующими. На сегодняшний день механизмы пульсирующего течения в элементах различного теплообменного оборудования раскрыты недостаточно и находятся на начальном этапе развития [7, 8].

При исследовании пульсирующих течений с целью интенсификации теплообмена в целом получены положительные результаты. Возможность интенсифицировать теплообмен при вынужденных пульсациях потока исследована при течении в трубе [9], обтекании цилиндра [10], пористых сред [11], одиночных выступов [12], волнистых каналов [13] и т. д.

В работах [14,15] экспериментальным методом исследовано течение в пучках труб при пульсациях потока. Используя лазерный доплеровский анемометр, авторы проанализировали гидродинамическую картину течения в различных компоновках пучков труб. Влияние пульсаций на теплообмен не исследовалось. В работе [16] исследовалась теплоотдача коридорного пучка труб численным методом. Получена интенсификация теплообмена первого и второго ряда. Авторы установили, что увеличение теплоотдачи цилиндра первого и второго ряда связано с феноменом резонанса вихрей. Интенсификации теплообмена для остальных рядов при вынужденных пульсациях не наблюдалось. В работе [17] численным методом исследован теплообмен при симметричных пульсациях в шахматном пучке труб. Количество рядов по потоку было 18. Показано, что интенсификация теплообмена зависит от параметров пульсаций и ряда трубки в пучке. В ряде исследований [18, 19] показано, что вынужденная нестационарность, наложенная на поток воздуха, приводит к увеличе- нию теплоотдачи пучков труб. В работах [20, 21] исследовался внешний теплообмен шахматного пучка труб при симметричных осцилляциях потока. Пучки труб погружались в специальный бассейн, в котором генерировались симметричные колебания потока. В результате исследований получено, что интенсификация теплообмена практически пропорциональна амплитуде пульсаций и не зависит от частоты пульсаций. В работе [22] проведено численное исследование теплообмена в шахматном пучке труб при пульсирующем потоке. Показано, что интенсификация теплообмена различна в зависимости от ряда цилиндра в пучке труб. Получено, что теплоотдача первого ряда в пучке труб при пульсациях потока увеличивается на 16 %, последующих рядов – на 7 %.

Научная новизна

Несмотря на имеющие в литературе единичные работы, пульсирующие течения в пучках труб не изучены в полной мере и требуют дальнейших исследований. При этом пульсации в имеющихся работах имеют ограниченную амплитуду и симметричный характер пульсаций. Пульсации потока могут носить как симметричный, так и несимметричный характер. Эффективность несимметричных пульсаций с возвратно-поступательными пульсациями показана в работах [23, 24]. Научная новизна работы заключается в том, что получены закономерности распределения теплоотдачи по глубине коридорного пучка труб в условиях несимметричных возвратно-поступательных пульсаций потока. В этой работе представлены результаты численных исследований локального теплообмена в зависимости от ряда цилиндра в пучке труб при несимметричных пульсациях для различных частот и амплитуд пульсаций.

Постановка задачи

Изучаемая проблема – это двумерное течение при конвективном теплообмене в канале с пучком труб. Физическая постановка проблемы показана на рис. 1. По центру канала расположены семь рядов трубок диаметром D = 0,02 м в коридорном порядке. Относительный поперечный S1/D и продольный шаг S2/D пучка труб был 1,4. Входная и выходная буферная область была равной 5D. Температура стенок цилиндров была принята постоянной tw = 317 К. Температура входящего потока была ниже на одни градус температуры стенок tf = 316 К. На выходе задавалось давление окружающей среды P = 101 325 Па. При стационарном течении на входе задавалась постоянная скорость потока u = 1,335 · 10-2 м/с. На верхней и нижней границе расчетной области было принято условие симметрии ∂u/∂n = 0, ∂P/∂n = 0, ∂t/∂n = 0. Было принято, что свойства жидкости не зависят от температуры, сила гравитации не учитывалась. В качестве рабочей среды была выбрана вода. Теплофизические свойства были постоянными и задавались числом Прандтля, которое принималось Pr = 4,03. Теплопроводность воды была принята λ = 0,639 Вт/(м · К), динамическая вязкость µ = 6,174 · 10-4 Па · с, плотность ρ = 991,14 кг/м3, теплоемкость cp = 4173,13 Дж/(кг · К).

При нестационарном течении на входе устанавливалась зависимость скорости от времени, которая зависела от режима пульсаций. Пульсации имели возвратно-поступательный несимметричный характер с различной частотой f и относительной амплитудой A / D , где A – обратный ход жидкости в пучке труб, м.

Частота пульсаций f определялась по формуле f = T1 Гц,                                  (1)

где Т - период пульсаций, который рассчитывался по формуле

T = T 1 + T 2 c,                                (2)

где Т ₁ и Т ₂ - первый и второй полупериод пульсаций соответственно.

Скважность пульсаций ψ рассчитывалась следующим образом:

ψ = ^T _T ¹ .                                     (3)

Для примера на рис. 2 приведена форма пульсаций скорости от безразмерного времени τ / T при амплитуде A / D = 0,4 и частоте f = 0,4 Гц. Число Рейнольдса как при стационарном, так и при пульсационном течении базировалось на диаметре цилиндра и скорости в самом узком сечении. Входная скорость, приведенная на рис. 2, уменьшалась в соответствии с различием в сечениях на входе и в самом узком сечении для достижения необходимого числа Рейнольдса Re. Осредненная скорость жидкости за период пульсаций была равной стационарной скорости. Таким образом, числа Рейнольдса при стационарном и пульсационном течении были равны.

В таблице приведены режимные параметры, исследованные при численном моделировании.

Рис. 1. Расчетная область численной модели Fig. 1. The computational domain of numerical model

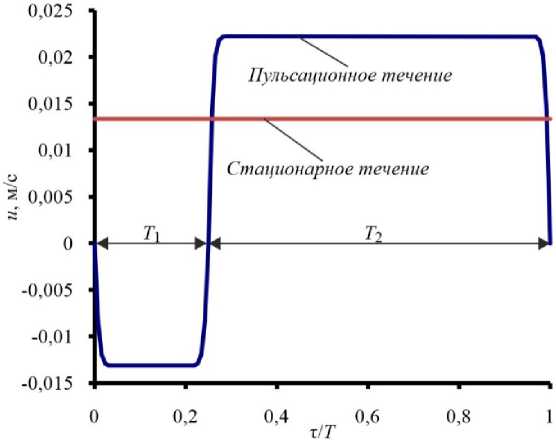
Рис. 2. Характер скорости потока при A / D = 0,4, f = 0,4 Гц и Re = 1500 на входе в пучок труб Fig. 2. Flow velocity shape at the inlet of tube bundle for A / D = 0.4, f = 0.4 Hz and Re = 1500

Режимные параметры Regime parameters

№	Re	ψ	A / D	f , Гц
1	1500	0,25	0,1	0,2
2	1500	0,25	0,1	0,4
3	1500	0,25	0,1	0,6
4	1500	0,25	0,1	0,8
5	1500	0,25	0,2	0,2
6	1500	0,25	0,2	0,4
7	1500	0,25	0,2	0,6
8	1500	0,25	0,2	0,8
9	1500	0,25	0,3	0,2
10	1500	0,25	0,3	0,4
11	1500	0,25	0,3	0,6
12	1500	0,25	0,3	0,8
13	1500	0,25	0,4	0,2
14	1500	0,25	0,4	0,4
15	1500	0,25	0,4	0,6
16	1500	0,25	0,4	0,8

Теоретическая часть

Конвективное несжимаемое течение описывалось уравнениями Навье – Стокса и Фурье – Кирхгофа [25]. В качестве модели турбулентности была выбрана модель RNG k- ε с улучшенной пристеночной функцией (RNG k- ε EWT), она показала удовлетворительное совпадение с экспериментальными данными при конвективном течении в пучке труб [22].

Численное исследование проводилось посредством AnsysFluent 19.2. При проведении расчетов использовался алгоритм SIMPLE. Стационарное течение разрешалось в стационарной постановке, при пульсационном режиме использовалась нестационарная постановка с шагом по времени 10–3 с, при этом количество итераций на каждом шаге было не более 20. Невязка для уравнения энергии была принята 10–6, для остальных уравнений 10–4.

В работе [22] было показано, что минимальный размер сеточных элементов y_min , отнесенный к диаметру цилиндра пучка труб y min / D = 3,16 · 10^–2, достаточен при моделировании конвективной теплоотдачи в пучке труб. В этой статье было принято y min / D = 3,16 · 10^–2, с 16 слоями в пристеночной области, которые расширялись в радиальном направлении с коэффициентов 1,22.

Число Нуссельта для каждого ряда в пучке труб рассчитывалось отдельно:

Nu = ^{q z D} , λΔ t_z

где z - номер ряда цилиндра в пучке труб прини- мало значение от 1 до 7; qz - плотность теплового потока, осредненная по поверхности цилиндра и за один период пульсаций, Вт/м2; Atz - разница температур между стенкой цилиндра tw и осредненной температурой жидкости вокруг цилиндра за один период пульсаций:

Д t z = t w - t - ° С, (5)

где t z - осредненная температура жидкости на входе в соответствующий ряд пучка, °С.

Результаты численного эксперимента

Для верификации математической модели число Нуссельта для стационарного течения при числе Рейнольлдса Re = 1500 сравнивалось с известным критериальным уравнением [3]. Разница числа Нуссельта для шестого ряда трубного пучка составила 10 %.

На рис. 3 приведена зависимость числа Нуссельта от ряда цилиндра z при минимальной и максимальной амплитуде пульсаций и стационарном течении на различных частотах пульсаций.

Из рис. 3 видно, что теплоотдача в пучке труб увеличивалась в зависимости от положения цилиндра в пучке труб как при стационарном, так и при пульсационном течении. Влияние положения цилиндра в пучке труб на теплообмен в пульсационном течении подобно стационарному течению. Теплоотдача цилиндра, находящегося в первом ряду, имеет минимальное значение. Значительное увеличение теплоотдачи происходит на втором ряду пучка труб, далее рост теплоотдачи замедляется вплоть до предпоследнего ряда, влияние последнего ряда превосходит влияние центральных рядов. Данная тенденция более выражена при стационарном течении и замедляется с увеличением частоты пульсаций. При стационарном течении теплоотдача второго ряда по сравнению с первым рядом увеличивается на 1,19, шестого ряда по сравнению со вторым рядом – на 1,038 последнего ряда по сравнению с предпоследним – на 1,035. При частоте пульсаций f = 0,8 Гц и амплитуде пульсаций A/D = 0,1 теплоотдача центральных рядов практически не меняется, разброс числа Нуссельта составляет не более 0,3 %. Увеличение теплоотдачи второго ряда связано с увеличением турбулентности течения, поскольку второй ряд находится в зоне вихреобразования первого ряда. Замедление роста теплоотдачи на последующих рядах связано с гомогенизацией потока. Данные результаты согласуются с экспериментальными данными, приведенными в работе [3]. Увеличение теплоотдачи последнего ряда связано с образованием вихреобразования в следе последнего цилиндра.

На рис. 4 показана зависимость числа Нуссельта от ряда цилиндра в пучке труб при различных амплитудах пульсаций. С увеличением амплитуды (см. рис. 4), как и с увеличением частоты (см. рис. 3), влияние ряда цилиндра уменьшается, максимальный рост теплоотдачи с изменением ряда также наблюдается на втором ряду. Значения числа Нуссельта первого и последнего ряда приближаются к значениям центральных рядов в пучке труб. При минимальной частоте и минимальной амплитуде (см. рис. 3) теплоотдача второго ряда увеличивалась на 1,18 раза, при максимальной частоте и амплитуде (см. рис. 4) рост теплоотдачи второго ряда по сравнению с первым составил 1,07 раза.

На рис. 5, 6 показано, как интенсификация теплообмена зависит от ряда цилиндра в пучке труб при различных режимных параметрах пульсаций. Увеличение теплообмена оценивалось с помощью отношения числа Нуссельта при пульсационном течении Nu p к числу Нуссельта при стационарном

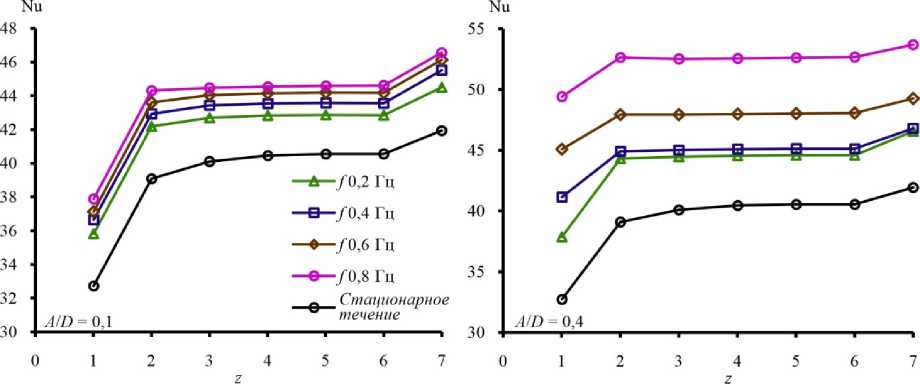
Рис. 3. Зависимость числа Нуссельта от ряда пучка труб при амплитуде пульсаций

A / D = 0,1, A / D = 0,4 и различной частоте пульсаций

Fig. 3. The dependence of the Nusselt number on the row of a tube bundle at pulsation amplitudes

A / D = 0.1, A / D = 0.4 and for different pulsation frequencies

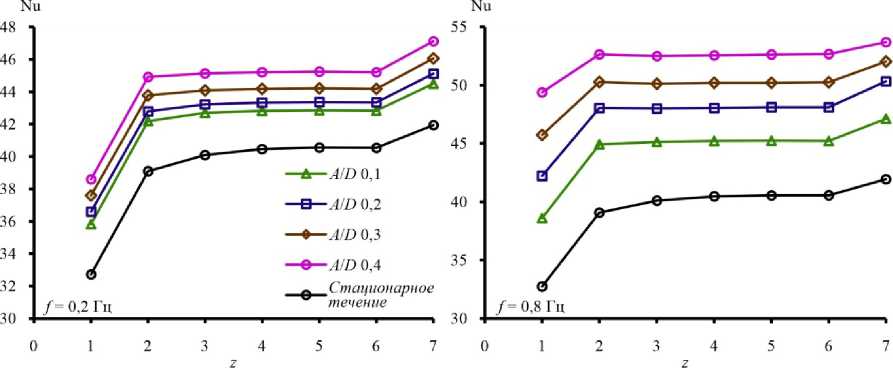
Рис. 4. Зависимость числа Нуссельта от ряда пучка труб при частоте пульсаций f = 0,2 Гц, f = 0,4 Гц и различной амплитуде пульсаций

Fig. 4. The dependence of the Nusselt number on the row of a tube bundle at pulsation frequencies f = 0.2 Hz, f = 0.4 Hz and for different pulsation amplitudes

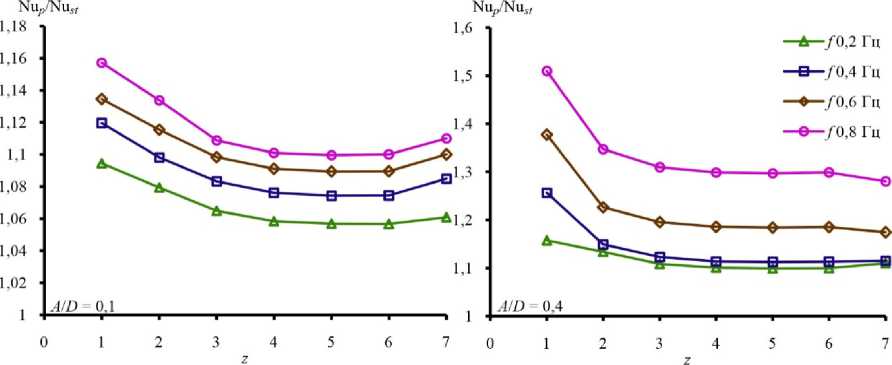
Рис. 5. Зависимость прироста числа Нуссельта от ряда пучка труб при амплитуде пульсаций A / D = 0,1, A / D = 0,4 и различной частоте пульсаций

Fig. 5. The dependence of the Nusselt number ratio on the row of the tube bundle at pulsation amplitudes A / D = 0.1, A / D = 0.4 and for different pulsation frequencies

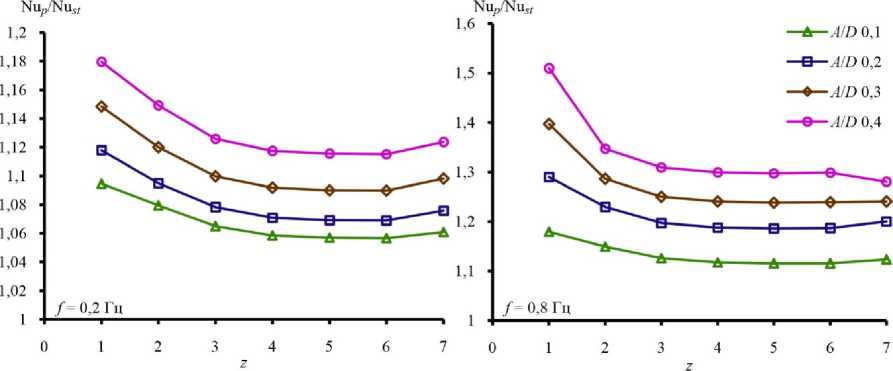
Рис. 6. Зависимость прироста числа Нуссельта от ряда пучка труб при частоте пульсаций f = 0,2 Гц, f = 0,4 Гц и различной амплитуде пульсаций

Fig. 6. The dependence of the Nusselt number ratio on the row of a tube bundle at pulsation frequencies f = 0.2 Hz, f = 0.4 Hz and for different pulsation amplitudes течении Nust. Из рис. 5, 6 видно, что интенсификация теплообмена различна в зависимости от ряда цилиндра в пучке труб. Различная интенсификация по рядам пучка труб также получена в работах [16, 17]. В работе [16] увеличение теплоотдачи при пульсационном течении в пучке труб было зафиксировано только для первого ряда, теплоотдача остальных рядов трубного пучка практически не менялась. Отсутствие интенсификации теплоотдачи глубинных рядов связано с меньшей амплитудой пульсаций без возвратно-поступательного течения. В данном исследовании амплитуда пульсаций имела возвратно-поступательный характер. В [17] так же, как и в данной работе, наблюдалось уменьшение интенсификации теплообмена по глубине пучка труб.

Максимальное увеличение прироста числа Нуссельта независимо от частоты и амплитуды пульсаций наблюдается на первом ряду, что связа- но с возвратно-поступательным характером пульсаций. При пульсирующем течении в связи с разворотом потока первый ряд в пучке труб на некоторый промежуток времени становится последним, что приводит к увеличению его теплоотдачи в связи с ростом вихреобразования в следе цилиндра. С увеличением ряда интенсификация теплообмена уменьшается. Например, при частоте f = 0,8 Гц и амплитуде A/D = 0,1 (см. рис. 5) прирост числа Нуссельта первого, второго и третьего ряда был 1,16; 1,13 и 1,11 соответственно, при этом на последнем ряду интенсификация теплообмена снова увеличивается. При амплитуде A/D = 0,1 и частоте f > 0,2 Гц прирост числа Нуссельта последнего ряда выше центральных рядов, но меньше второго ряда. С увеличением амплитуды пульсаций при фиксированной частоте (см. рис. 5) и при фиксированной амплитуде с увеличением частоты (см. рис. 6) влияние ряда на отношение числа Нуссельта снижается.

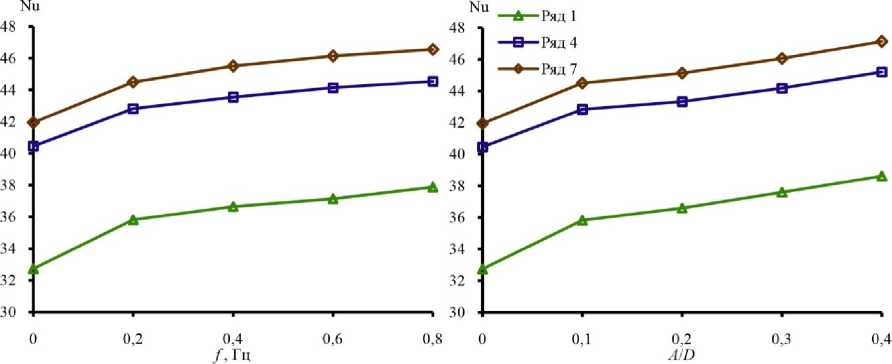
Рис. 7. Зависимость числа Нуссельта от частоты и амплитуды пульсаций для различных рядов пучка труб

Fig. 7. The dependence of the Nusselt number on the frequency and the amplitude of pulsations for various rows of a pipe bundle

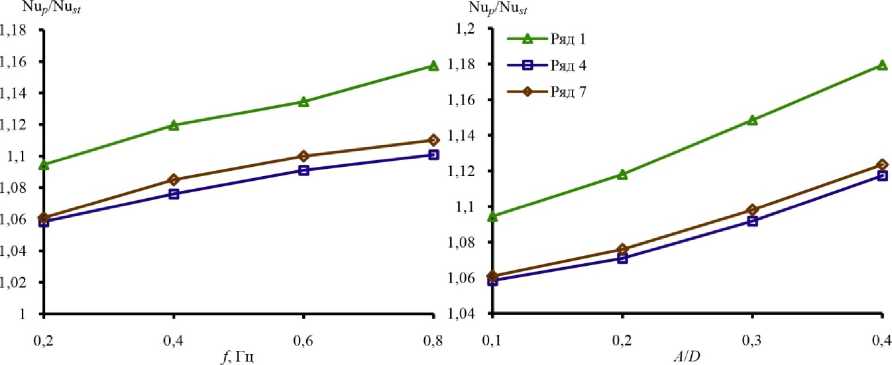
Рис. 8. Зависимость прироста числа Нуссельта от частоты и амплитуды пульсаций для различных рядов пучка труб

Fig. 8. The dependence of the Nusselt number ratio on the frequency and the amplitude of pulsations for various rows of a pipe bundle

На рис. 7, 8 показано влияние частоты и амплитуды пульсаций на число Нуссельта и прирост числа Нуссельта. Из рис. 7 отчетливо видно, что увеличение частоты и амплитуды пульсаций приводит к повышению числа Нуссельта независимо от ряда пучка труб, при этом изменение числа Нуссельта более выражено при минимальной частоте и амплитуде пульсаций. Число Нуссельта в пульсационном течении по сравнению со стационарным течением (см. рис. 8) увеличивается с ростом амплитуды и частоты пульсаций независимо от ряда пучка труб. Из рис. 8 также видно, что прирост числа Нуссельта максимален на первом ряду пучка труб.

При экспериментальных исследованиях теплообмена в пучках труб с симметричными пульсациями потока в работе [18] достигнута интенсификация теплообмена в 1,42 раза, что близко к значению в 1,51 раза, полученному в данном исследовании. В работе [18] частота пульсаций была выше, чем в нашем исследовании, при этом амплитуда пульсаций не имела возвратно-поступательный характер. В работе [18] увеличение частоты, как и в данном исследовании, приводило к росту теплоотдачи. В другой работе при численном моделировании в пучке труб увеличение частоты пульсаций также приводило к росту теплообмена. В работе [21] при экспериментальном исследовании теплообмена в пучке труб с симметричными колебаниями жидкости было достигнуто увеличение теплоотдачи в 2 раза. Относительная амплитуда колебаний в работе [21] была 18,5 диаметра трубки пучка, что значительно превосходило амплитуду, принятую в данном исследовании. При увеличении амплитуды пульсаций в работе [21] происходил рост интенсификации теплообмена, что согласуется с результатами настоящего исследования.

На рис. 9 показаны контуры скорости в пучке труб при стационарном течении. На рис. 10 представлены контуры скорости при фиксированной частоте и амплитуде для различных фаз пульсаций. При пульсационном течении наблюдаются локальные изменения скоростей с перестройкой потока, что способствует интенсификации теплообмена. В зависимости от фаз пульсаций при пульсирующем течении скорость потока ниже стационарной скорости или превосходит стационарное течение. Скорость потока ниже при развороте потока, что соответствует фазам пульсаций τ/T = 0,1 и τ/T = 0,2. При фазах пульсаций τ/T < 0,2 направление потока противоположно направлению стационарного потока. При фазах пульсаций τ/T > 0,2 направление потока совпадает со стационарным течением, при этом скорость превосходит стационарное течение.

Практическая значимость

Полученные результаты могут быть учтены при прогнозировании теплоотдачи в трубчатых теплообменниках при вынужденных пульсациях потока. Полученное в ходе численного моделирования увеличение теплообмена говорит о потенциальной возможности применении вынужденных пульсаций для повышения эффективности трубчатых теплообменных аппаратов. Интенсификация теплообмена позволяет снизить металлоемкость теплообменной поверхности аппаратов. Одним из преимуществ пульсационного метода интенсификации теплообмена является то, что он позволяет увеличить теплопроизводитель-ность существующего теплообменного аппарата без его разбора. Необходимость увеличения теп-лопроизводительности существующего теплообменного оборудования может возникать, например, при увеличении пиковых нагрузок, загрязнении теплообменной поверхности и др. В ходе численного моделирования показано, что интенсификация теплообмена зависит от ряда цилиндра в пучке труб, при этом максимальная интенсификация теплообмена наблюдается в первых рядах пучка труб. Поэтому применение пульсаций для исследованных в работе режимных параметров более эффективно для пучков с меньшим числом рядов.

Скорость U, м/с

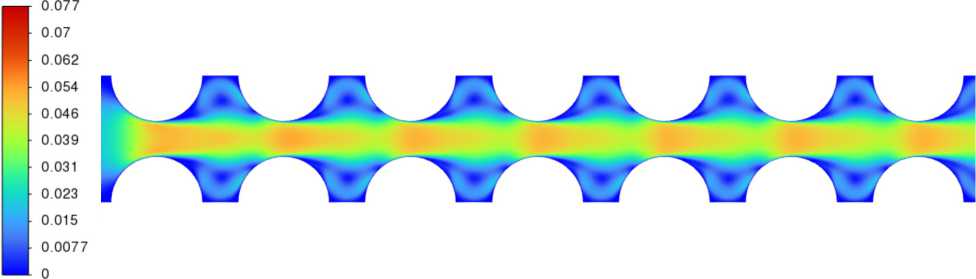
Рис. 9. Контуры скорости при стационарном течении Fig. 9. Velocity contours at a steady flow

т/Г=0,1

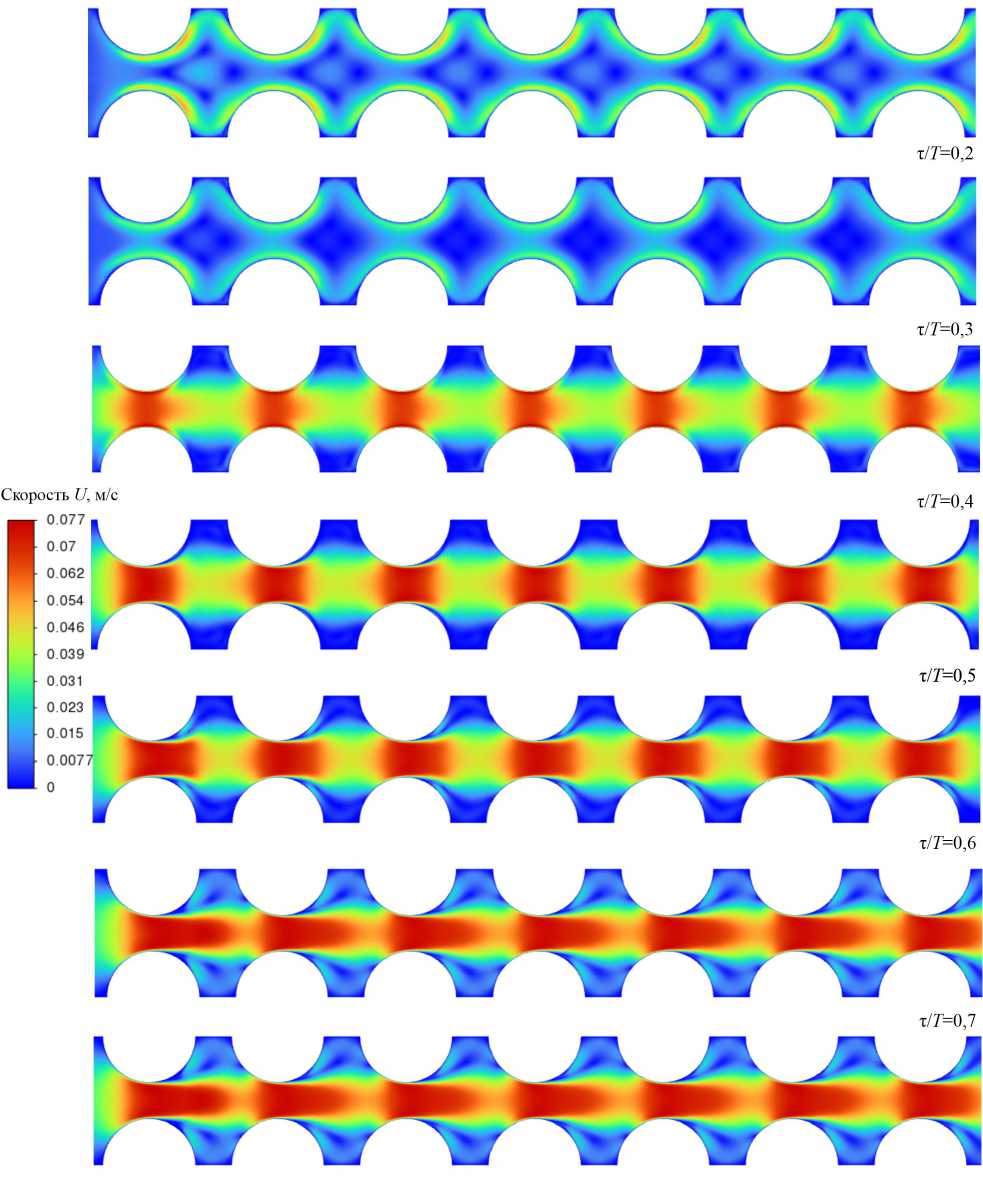
Рис. 10. Контуры скорости при пульсационном течении для разных фаз пульсаций при частоте f = 0,4 Гц и амплитуде A / D = 0,2

Fig. 10. Velocity contours during a pulsating flow for different pulsation phases at frequency f = 0.4 Hz and amplitude A / D = 0.2

Заключение

В работе на основе коммерческого продукта Ansys Fluent 19.2 проведено численное моделирование теплообмена в коридорном пучке труб при несимметричных пульсациях потока. Установлено, что как при стационарном, так и пульсационном течении с увеличением положения цилиндра по глубине пучка происходит увеличение теплоотдачи цилиндра. Существенное увеличение теплоотдачи по сравнению с другими рядами наблюдается на первом и последнем ряду пучка труб, при этом данная тенденция уменьшается с увеличением частоты и амплитуды пульсаций. Увеличение частоты и амплитуды пульсаций приводит к увеличению теплообмена независимо от расположения цилиндра по глубине пучка труб. Максимальная интенсификация теплообмена в 1,51 раза наблю- далась для первого ряда при частоте f = 0,8 Гц и амплитуде A/D = 0,4, при этом интенсификация последующих рядов составила не более 1,34 раза. Минимальная интенсификация в 1,06 раза наблюдалась для рядов 4–7 при частоте f = 0,2 Гц и амплитуде A/D = 0,1.