Влияние сдвига распределения на точность сегментации объектов с помощью свёрточной нейронной сети

Автор: А. С. Чумаков, И. И. Лычков

Журнал: Современные инновации, системы и технологии.

Рубрика: Управление, вычислительная техника и информатика

Статья в выпуске: 5 (2), 2025 года.

Бесплатный доступ

Нейронные сети широко используются для распознавания объектов в задачах компьютерного зрения. Снижение точности распознавания объектов при отклонении статистических параметров тестовой выборки от статистических параметров обучающей выборки известно как явление сдвига распределения. В настоящей работе исследуется влияние сдвига распределения на точность сегментации объектов на цифровых изображениях. Значительная часть существующих работ в данной области имитирует явление сдвига распределения за счет применения специальных эффектов к реальным цифровым изображениям. Такой подход ограничивает набор варьируемых параметров и сокращает возможности исследования сдвига распределения. Особенностью настоящей работы является синтез исходных цифровых изображений объектов простой геометрической формы для оценки влияния сдвига распределения на точность сегментации объектов. Предложенный подход позволяет получить больший контроль над процессом обучения и тестирования нейронной сети и охватить больший набор варьируемых параметров распределения. В качестве изменяемых параметров были выбраны ширина и высота фигуры, угол поворота фигур и всего изображения, цветовые компоненты изображения, накладываемый шум и степень взаимного перекрытия фигур.

Еще

Сдвиг распределения, Mask R-CNN, свёрточная нейронная сеть, сегментация объектов, синтетические изображения

Короткий адрес: https://sciup.org/14133030

IDR: 14133030 | DOI: 10.47813/2782-2818-2025-5-2-3077-3085

Текст статьи Влияние сдвига распределения на точность сегментации объектов с помощью свёрточной нейронной сети

DOI:

В последние годы наблюдается активное развитие различных нейронных сетей, в частности моделей по анализу изображений. К подобным моделям относится семейство свёрточных нейронных сетей (англ. Convolutional Neural Network, сокр. CNN). Одним из его представителей является модель Mask R-CNN (англ. Mask Region-based Convolutional Neural

Network) [1]. Это метод глубокого обучения для одновременного обнаружения объектов, классификации и сегментации масок этих объектов на изображениях. Схема его работы приведена на рисунке 1, где RoIAlign (Region of Interest Alignment) – слой, выравнивающий регионы интереса из свёрточных карт признаков, conv – свёрточный слой, class box – классификатор классов для объектов в регионах интереса.

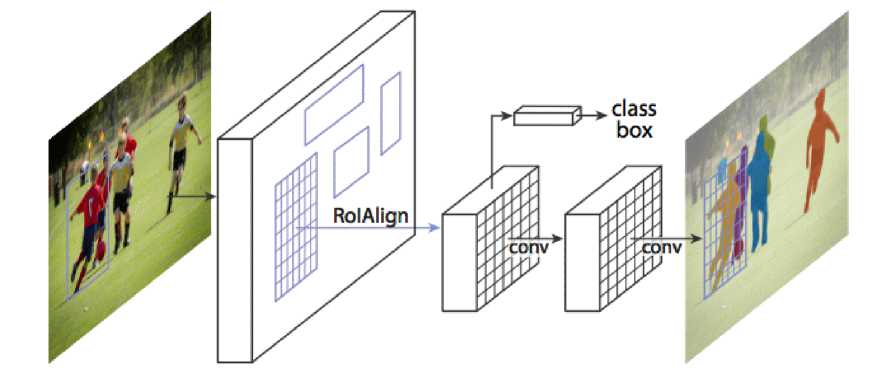
Рисунок 1. Принцип работы M ASK R-CNN [1, 1].

Figure 1. Mask R-CNN working principle [1, 1].

Как и любая модель искусственного интеллекта, Mask R-CNN чувствительна к сдвигу распределения, ситуации, при которой распределение данных в тестовой выборке отлично от распределения данных в обучающей выборке. Сдвиг распределения приводит к нежелательному падению точности работы модели, что в свою очередь является предметом научных исследований.

Первая группа исследований [2-6] фокусируется на повышении устойчивости моделей к сдвигам распределения, предлагая использование различных методов. Так, в статьях [2] и [5] разрабатываются методологии построения доверительных интервалов, обеспечивающих правильную оценку при возникновении сдвига распределения. В статьях [3] и [4] предлагаются методы по повышению надежности мультимодальных моделей, а статья [6] рассматривается влияние тонкой настройки модели на её способность выявлять сдвиги распределения.

Вторая группа исследований [7-9] занимается более детальным изучением влияния сдвига распределения на предсказания моделей. В этих статьях в качестве изменяемых данных берутся реальные фотографии, к которым применяется различная постобработка. Это может быть как добавление на изображение имитации различных погодных условий [8-9], так и добавление стандартных шумов и искажений [7][9]. Из-за использования реальных изображений в качестве основы накладываются ограничения на гибкость модификаций, которая бы могла пригодится для дальнейшего анализа.

Цель работы – используя сгенерированные с нуля изображения, пронаблюдать работу модели Mask R-CNN при различных по величине и характеру сдвигах распределения. Это позволит оценить поведение модели в нестандартных для неё условиях, что в свою очередь поможет сформулировать требования к тестовым данных, следуя которым получится сохранять требуемый уровень точности предсказаний.

МАТЕРИАЛЫ И МЕТОДЫ

Для проведения экспериментов требуются сегментирующая объекты на изображении модель и данные, на которых модель будет обучаться и тестироваться. Данные получаются из специального генератора, который позволяет гибко регулировать их параметры. Для каждого из экспериментов генерируется несколько наборов данных: набор для обучения модели с исходными параметрами и несколько наборов для тестирования модели с равномерно изменяющимся сдвигом распределения. В процессе обучения и последующего тестирования модели на обозначенных наборах данных фиксируется точность предсказаний и впоследствии анализируется.

Для создания набора данных был написан генератор, который на основе переданного конфигурационного файла создает требуемое количество изображений, содержащих объекты простой геометрической формы. Помимо исходных изображений генератор создает маски объектов на них, которые впоследствии используются для обучения модели и оценки точности предсказания, и файл с метаданными, необходимый для работы модели. Схема работы генератора данных приведена на рисунке 2. Сами изображения были в формате PNG, размером 320 на 320 пикселей и содержали по 5 объектов на каждом.

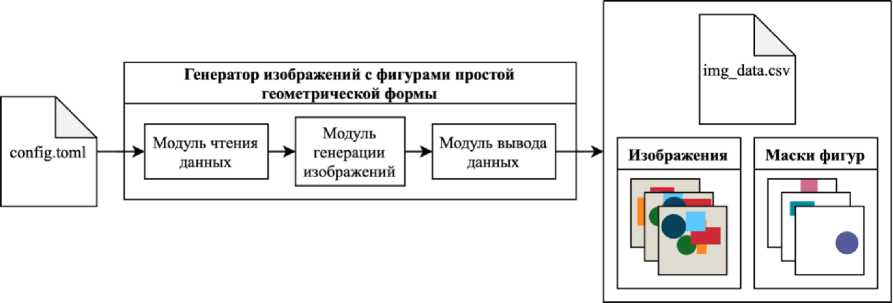
Рисунок 2. Принцип работы генератора изображений.

Figure 2. Image generator working principle.

Обозначенный генератор позволяет создавать набор данных с указанными параметрами. Для создания множества наборов данных применяется мета-генератор, для которого можно указывать шаг сдвига распределения. Таким образом, описав общий конфигурационный файл, в котором приведены настройки данных для всех экспериментов, можно при помощи метагенератора получить все требуемые данные.

В качестве модели, как было сказано ранее, используется Mask R-CNN. Модель доработана для работы с теми данными, которые выдает генератор. Обучение выполняется за десять эпох батчами по четыре элемента со скоростью обучения 0,01, которая уменьшается в 10 раз каждые три эпохи. Объем выборок составил 3500 элементов для обучающей и 300 для тестовых. Для каждого эксперимента создавалось по три тестовых выборки, а в дальнейшем по результатам брались значения точности с посчитанным доверительным интервалом. Перед поступлением на вход модели изображение случайным образом отражается по вертикали и/или горизонтали для повышения качества обучения.

Подход по расчету точности опирается на концепцию, предложенную в VOC2008 [10] и представленную следующим выражением:

точность =

TP+ FP + FN

где TP – верно определенные пиксели объекта (True Positives), FP – ложно определенные пиксели объекта (False Positives), FN – ложно не определенные пиксели объекта (False Negatives).

Эксперименты разбиты на 10 групп. В каждой группе проверяется влияние сдвига распределения одного конкретного параметра. Распределения остальных параметров остаются при этом неизменными. Исследуемые параметры выбраны следующие: ширина и/или высота фигур, поворот отдельных фигур и всего изображения, цветовые каналы H, S и V фигур, шум, накладываемый на изображение и степень перекрытия фигур друг другом. Внутри группы экспериментов можно выделить 4 подгруппы, для каждой из которых менялась только одна из характеристик распределения: центр равномерного распределения, ширина равномерного распределения, центр нормального распределения и сигма нормального распределения.

РЕЗУЛЬТАТЫ

Для удобства представления полученных результатов введем ряд обозначений. Так, usegm и nsegm будут означать точность сегментации при использовании равномерного и нормального распределений соответственно. Данные значения будут приводится вместе с указанием доверительного интервала при доверительной вероятности 0,95. Также результаты тестов, полученные при параметрах сдвига распределения, которые использовались при обучении модели, для наглядности будут отмечены жирным курсивом.

Результаты экспериментов по изменению распределения размеров фигур приведены в таблицах 1 и 2. В качестве параметра, к которому применяются различные распределения, для данных экспериментов используется коэффициент, на который умножается ширина и/или высота фигуры по умолчанию.

Таблица 1. Точность сегментации при сдвиге центра распределения размера ( ШИРИНЫ и высоты), высоты и ширины фигур НА ИЗОБРАЖЕНИИ .

Table 1. Segmentation accuracy when shifting the distribution’S center of size (width and height), height and width of shapes in the image.

Центр сдвига распределения	Размер фигур		Высота фигур		Ширина фигур
Центр сдвига распределения	u segm , %	n segm , %	u segm , %	n segm , %	u segm , %	n segm , %
0,3	83,2 ± 1,07	-	82 ± 1,1	-	75,3 ± 1,07	-
0,4	91 ± 0,28	-	90,1 ± 0,25	-	88,1 ± 0,94	-
0,5	95 ± 0,14	94,9 ± 0,17	93 ± 0,08	93,5 ± 0,4	93,3 ± 0,29	93,5 ± 0,24
0,6	95,6 ± 0,2	95,6 ± 0,16	94,2 ± 0,25	94,5 ± 0,19	94,6 ± 0,17	94,4 ± 0,24
0,7	95,9 ± 0,03	95,6 ± 0,07	94,6 ± 0,22	94,6 ± 0,16	94,9 ± 0,16	94,8 ± 0,13
0,8	95,3 ± 0,1	95,1 ± 0,3	94,5 ± 0,18	94,6 ± 0,19	94,8 ± 0,13	94,7 ± 0,26
0,9	94,8 ± 0,16	94,5 ± 0,09	94,4 ± 0,17	94,3 ± 0,2	94,6 ± 0,03	94,5 ± 0,06
1,0	94 ± 0,23	94 ± 0,1	94,2 ± 0,18	93,9 ± 0,06	94,2 ± 0,12	94 ± 0,26
1,1	92,7 ± 0,04	92,7 ± 0,06	93,4 ± 0,09	93,4 ± 0,21	93,5 ± 0,16	93,5 ± 0,25
1,2	91,1 ± 0,16	91,2 ± 0,11	92,7 ± 0,21	92,8 ± 0,45	92,6 ± 0,19	92,7 ± 0,16
1,3	88,2 ± 0,79	89,8 ± 0,34	91,5 ± 0,04	91,9 ± 0,23	91,6 ± 0,17	91,5 ± 0,58
1,4	84,9 ± 0,36	86,6 ± 0,45	90,1 ± 0,23	90,5 ± 0,15	89,9 ± 0,26	90,2 ± 0,43
1,5	79,9 ± 0,99	83,6 ± 0,75	88,4 ± 0,32	89,1 ± 0,3	86,9 ± 0,44	89,3 ± 0,65
1,6	74 ± 0,65	-	86,1 ± 0,28	-	84,6 ± 0,3	-
1,7	67,4 ± 0,11	-	83,5 ± 0,26	-	81,6 ± 0,28	-

Таблица 2. Точность сегментации при сдвиге Δ / Σ распределения размера ( ШИРИНЫ и высоты), высоты и ширины фигур на ИЗОБРАЖЕНИИ .

Table 2. Segmentation accuracy when shifting the distribution Δ/ Σ of size (width and height), height and width of shapes in the image.

Δ/σ	Размер фигур		Высота фигур		Ширина фигур
Δ/σ	u segm , %	n segm , %	u segm , %	n segm , %	u segm , %	n segm , %
0,05	-	94,1 ± 0,08	-	94,2 ± 0,15	-	94,1 ± 0,31
0,1	94,2 ± 0,15	94,1 ± 0,08	94,3 ± 0,06	94,1 ± 0,12	93,9 ± 0,24	93,9 ± 0,42
0,15	-	93,8 ± 0,35	-	93,7 ± 0,17	-	93,9 ± 0,15
0,2	93,9 ± 0,1	93,5 ± 0,04	94 ± 0,3	93,8 ± 0,36	94,3 ± 0,16	93,8 ± 0,31
0,25	-	93,2 ± 0,22	-	93,5 ± 0,35	-	93,7 ± 0,11
0,3	93,4 ± 0,39	92,3 ± 0,36	94 ± 0,13	93,5 ± 0,23	94 ± 0,48	93,5 ± 0,34
0,4	93,3 ± 0,22	-	93,5 ± 0,14	-	93,8 ± 0,48	-
0,5	92,5 ± 0,24	-	93,7 ± 0,18	-	93,6 ± 0,14	-

Результаты экспериментов по изменению распределения поворота фигур и всего изображения приведены в таблицах 3 и 4. В качестве параметра, к которому применяются различные распределения, для данных экспериментов используется значение в градусах, которое прибавляется к значению поворота по умолчанию.

Таблица 3. Точность сегментации при сдвиге центра распределения поворота фигур на изображении и всего ИЗОБРАЖЕНИЯ .

Table 3. Segmentation accuracy when shifting the distribution’S center of rotation of shapes in the image and whole image.

Центр сдвига распределения	Поворот фигуры		Поворот изображения
Центр сдвига распределения	u segm , %	n segm , %	u segm , %	n segm , %
0	94 ± 0,15	93,7 ± 0,14	94 ± 0,28	91,1 ± 0,36
10	92,8 ± 0,41	93,2 ± 0,23	92,7 ± 0,13	88,5 ± 0,22
20	90,4 ± 0,35	91,7 ± 0,15	90,8 ± 0,21	82,6 ± 0,12
30	86,6 ± 0,44	89,6 ± 0,6	86,5 ± 0,5	75,7 ± 0,83
40	81,7 ± 0,32	87,1 ± 0,24	81,6 ± 0,09	69,5 ± 0,47
50	77,2 ± 0,49	84,9 ± 0,15	78,2 ± 0,18	66,6 ± 0,18
60	75,1 ± 0,4	82,4 ± 0,75	76,6 ± 0,65	68,2 ± 0,91
70	76,6 ± 0,21	81,4 ± 0,62	77,9 ± 0,42	70,9 ± 0,49
80	76,9 ± 0,68	79,9 ± 0,81	78,5 ± 0,62	73,8 ± 0,48
90	77,5 ± 0,63	78,7 ± 0,8	78,1 ± 0,95	75,4 ± 0,79

Таблица 4. Точность сегментации при сдвиге Δ / Σ распределения поворота фигур на изображении и всего изображения.

Table 4. Segmentation accuracy when shifting the distribution Δ/ Σ of rotation of shapes in the image and whole image.

Δ/σ	Поворот фигуры		Поворот изображения
Δ/σ	u segm , %	n segm , %	u segm , %	n segm , %
5	-	94,2 ± 0,14	-	93,4 ± 0,08
10	94 ± 0,18	93,8 ± 0,09	94,2 ± 0,42	91 ± 0,05
15	-	93,1 ± 0,16	-	88,6 ± 0,56
20	93,2 ± 0,18	92,2 ± 0,16	93,1 ± 0,31	85,8 ± 0,34
25	-	91,4 ± 0,05	-	83,6 ± 1,08
30	91,6 ± 0,21	90,3 ± 0,15	91,7 ± 0,05	81,6 ± 0,48
35	-	89,8 ± 0,45	-	80,3 ± 0,39
40	89,6 ± 0,3	89,3 ± 0,39	90,1 ± 0,37	79,3 ± 0,58
45	-	88,2 ± 0,56	-	78,1 ± 0,19
50	87,6 ± 0,49	-	88 ± 0,14	-
60	85,9 ± 1,28	-	86,2 ± 0,39	-
70	84,8 ± 0,13	-	84,6 ± 0,46	-
80	83,5 ± 0,47	-	84,1 ± 0,4	-
90	82,8 ± 0,7	-	82,7 ± 0,16	-

Результаты экспериментов по изменению распределения цветовых характеристик изображения приведены в таблицах 5 и 6. В качестве параметра, к которому применяются различные распределения, для данных экспериментов используется значение, которое прибавляется к нормированному значению компоненты цвета. В качестве используемой цветовой модели была взята модель HSV.

Таблица 5. Точность сегментации при сдвиге центра распределения значения цветовой компоненты изображения.

Table 5. Segmentation accuracy when shifting the distribution’S center of image’S color component’S value.

Центр сдвига распределения	Тон (H)		Насыщенность (S)		Яркость (V)
Центр сдвига распределения	u segm , %	n segm , %	u segm , %	n segm , %	u segm , %	n segm , %
-0,5	71,9 ± 0,12	75,6 ± 0,42	89,1 ± 0,07	89,4 ± 0,06	87,9 ± 0,14	94,3 ± 0,17
-0,4	71,1 ± 0,57	76 ± 0,27	92,1 ± 0,18	92,4 ± 0,26	89,7 ± 0,25	94,4 ± 0,24
-0,3	74,1 ± 0,19	79,9 ± 0,2	93,4 ± 0,13	93,5 ± 0,22	92,6 ± 0,48	94,3 ± 0,23
-0,2	84,6 ± 0,66	88,9 ± 0,39	93,9 ± 0,09	93,8 ± 0,22	94,4 ± 0,29	94,4 ± 0,17
-0,1	92,2 ± 0,13	93 ± 0,11	94 ± 0,14	94 ± 0,21	94,2 ± 0,25	94,4 ± 0,13
0	94,4 ± 0,31	94 ± 0,32	94,2 ± 0,16	94,4 ± 0,25	94,4 ± 0,06	94,3 ± 0,25
0,1	92,4 ± 0,35	89,3 ± 0,54	94,5 ± 0,14	94,2 ± 0,26	94,5 ± 0,09	94,2 ± 0,21
0,2	88 ± 0,17	94 ± 0,1	94,4 ± 0,32	94,5 ± 0,26	94 ± 0,2	94,4 ± 0,19
0,3	82,6 ± 0,75	78,7 ± 0,56	94,2 ± 0,2	94,3 ± 0,34	92,7 ± 0,24	94,3 ± 0,08
0,4	76,1 ± 0,26	73,2 ± 0,58	94,2 ± 0,07	94 ± 0,09	89,1 ± 0,33	94,2 ± 0,23
0,5	72,4 ± 0,39	70,6 ± 0,44	93,2 ± 0,42	93,8 ± 0,36	83 ± 0,72	94,2 ± 0,09

Таблица 6. Точность сегментации при сдвиге Δ/ Σ распределения значения цветовой компоненты изображения.

Table 6. Segmentation accuracy when shifting the distribution Δ/ Σ of image’S color component’S value.

Δ/σ	Тон (H)		Насыщенность (S)		Яркость (V)
Δ/σ	u segm , %	n segm , %	u segm , %	n segm , %	u segm , %	n segm , %
0,05	94,2 ± 0,21	94,1 ± 0,07	94,3 ± 0,14	94,4 ± 0,17	94,4 ± 0,23	94,2 ± 0,06
0,1	94,2 ± 0,13	93,2 ± 0,23	94,5 ± 0,1	94,3 ± 0,07	94,4 ± 0,23	94,2 ± 0,03
0,15	93,7 ± 0,19	91,4 ± 0,47	94,2 ± 0,1	94,3 ± 0,25	94,4 ± 0,16	94,1 ± 0,21
0,2	92,2 ± 0,42	88,9 ± 1,16	94,2 ± 0,27	94 ± 0,19	94,3 ± 0,08	93,2 ± 0,12
0,25	90,8 ± 0,3	87,7 ± 0,91	94 ± 0,2	93,8 ± 0,46	94,2 ± 0,1	92,7 ± 0,24
0,3	89,5 ± 0,48	85,4 ± 0,73	94,5 ± 0,02	93,1 ± 0,19	94,1 ± 0,08	91,4 ± 0,02

Результаты экспериментов по изменению распределения шума, накладываемого на изображение, приведены в таблицах 7 и 8. В качестве параметра, к которому применяются различные распределения, для данных экспериментов используется значение условной переменной, которая отражает силу шума. Чем её модуль больше, тем больше шум. Нулевое значение переменной означает отсутствие шума.

Таблица 7. Точность сегментации при сдвиге центра распределения накладываемого на изображение шума.

Table 7. Segmentation accuracy when shifting the distribution’S center of noise applied to image.

Центр сдвига распределения	u segm , %	n segm , %
0	94,2 ± 0,19	94,3 ± 0,28
10	93,9 ± 0,06	94,2 ± 0,09
20	93,7 ± 0,17	94,3 ± 0,09
30	93,5 ± 0,2	93,8 ± 0,2
40	93 ± 0,25	93,2 ± 0,08
50	92,4 ± 0,02	92,8 ± 0,1

Таблица 8. Точность сегментации при сдвиге Δ/ Σ распределения накладываемого на изображение шума. Table 8. Segmentation accuracy when shifting the distribution Δ/ Σ of rotation of noise applied to image.

Δ	u segm , %	σ	n segm , %
10	94 ± 0,31	5	93,3 ± 0,04
20	94,1 ± 0,13	10	94,3 ± 0,23
30	94 ± 0,02	15	94,2 ± 0,21
40	94,2 ± 0,15	20	94,6 ± 0,17
50	93,9 ± 0,39	25	94,5 ± 0,13
60	93,6 ± 0,41	30	94,3 ± 0,2
70	93,5 ± 0,15	35	94,1 ± 0,21
80	92,9 ± 0,26	40	93,8 ± 0,1
90	92,6 ± 0,09	45	93,5 ± 0,26
100	91,8 ± 0,34	50	92,9 ± 0,15

Результаты экспериментов по изменению распределения перекрытия фигур друг другом приведены в таблицах 9 и 10. В рамках данного блока экспериментов на расположенные на изображении пять фигур накладывается ряд ограничений. Так, не более двух фигур могут иметь долю области видимости 85% и выше.

Также максимум одна фигура может иметь долю области видимости 10% и менее. Фигуры, не попавшие под обозначенные условия, должны иметь долю области видимости от 30% до 60%. Границы последнего интервала будут смещаться в силу применения распределений.

Таблица 9. Точность сегментации при сдвиге центра распределения допустимой доли видимости фигур.

Table 9. Segmentation accuracy when shifting the distribution’S center of figure’S allowed observable part’S interval.

Центр сдвига распределения, %	u segm , %	n segm , %
-20	88,8 ± 0,45	89,5 ± 0,21
-15	90,2 ± 0,37	90,5 ± 0,09
-10	91,2 ± 0,12	91,5 ± 0,14
-5	91,9 ± 0,08	91,4 ± 0,31
0	92,3 ± 0,14	92,1 ± 0,26
5	92,5 ± 0,24	92,7 ± 0,18
10	93 ± 0,34	92,9 ± 0,17
15	93,2 ± 0,58	93,2 ± 0,23
20	93,4 ± 0,34	92,8 ± 0,23

Таблица 10. Точность сегментации при сдвиге Δ/ Σ распределения допустимой доли видимости фигур.

Table 10. Segmentation accuracy when shifting the distribution Δ/ Σ of rotation of figure’S allowed observable part’S interval.

Δ, %	u segm , %	σ, %	n segm , %
5	92,2 ± 0,28	5	92,2 ± 0,19
10	92,2 ± 0,39	8	92,2 ± 0,12
15	92,2 ± 0,18	11	91,9 ± 0,15
20	92 ± 0,13	14	92,2 ± 0,45
25	91,9 ± 0,14	17	91,7 ± 0,36
30	91,4 ± 0,28	20	91,6 ± 0,35

ОБСУЖДЕНИЕ

Разберем результаты проведенных экспериментов. Рассмотрим не только эффект от сдвига распределения, но и приведем ситуацию из жизни, при которой такой сдвиг мог бы быть возможен. В дальнейшем это поможет сформировать рекомендации к использованию системы по сегментированию объектов на фотографии.

Эксперименты по изменению распределения ширины и/или высоты фигур могут моделировать отклонения фотографирующего устройства от положения, используемого при получении фотографий из обучающей выборки модели. Так, например, увеличение разброса ширины фигур как следствие искажения перспективы может возникнуть из-за шатающейся камеры на палубе корабля вследствие её недостаточно жесткого крепления в условия качки. По таблицам 1 и 2 видно, что точность сегментации заметно сильнее снижается при увеличении сдвига центра распределения ширины и/или высоты фигур, нежели при его уменьшении. При увеличении разброса распределения наблюдается тренд на снижение точности предсказаний, хоть и менее выраженный по сравнению со сдвигом центра распределения.

Эксперименты по повороту фигур моделируют хаотичное положение объектов на фото. Такую ситуацию можно встретить, рассматривая вещи пассажиров на ленте в зоне досмотра в аэропорту. Эксперименты по повороту всего изображения в свою очередь показывают возможное поведение системы при наклоне камеры относительно линии горизонта. Согласно данным из таблиц 3 и 4, при сильном повороте фигур в 60-90 градусов от исходного положения заметно снижается точность сегментации. Причем эффект при равномерном распределении выражен сильнее по сравнению с нормальным распределением. Схожие наблюдения можно сделать и для сдвига распределения поворота всего изображения.

Эксперименты по смещению сдвига распределения цветовых компонент могут быть полезны при оценке эффекта от избыточной или недостаточной освещенности сцены или особенностей матрицы камеры. Из таблиц 5 и 6 можно сделать наблюдение, что при отклонении центра распределения канала тона в любую сторону от нуля на более чем 0,2 приводит к значительному падению точности сегментации вплоть до 75% и ниже. Увеличение интервала распределения к столь сильному снижению точности не привело. Изменения распределения насыщенности практически не отражаются на точности предсказаний. Единственное, при сильном снижении насыщенности наблюдается заметное падение точности сегментации. Это объясняется тем, что фигуры становятся трудно различимы между собой. В случае с распределением яркости изменение ширины интервала распределения практически не оказывается эффекта. Однако большую роль играет смещение центра распределения. При его отклонении в любую сторону от нуля на более чем 0,2 приводит к постепенному падению точности сегментации вплоть до 85% и ниже.

Шум может появляться при съемке вследствие различных помех. Чем сильнее помехи, тем сильнее шум. Однако, как показывают результаты экспериментов из таблиц 7 и 8, влияние изменения распределения шума на точность крайне мало.

Эксперименты по изменению распределения интервалов области видимости фигур являются попыткой ответить на вопрос, насколько важно, чтобы объекты на сцене имели наименьшее количество пересечений с другими объектами. Результаты из таблиц 9 и 10 показывают, что с уменьшением области видимости точность сегментации падает, но незначительно, на 3-4%. Увеличение размера интервалов видимой доли эффекта практически не дает.

ЗАКЛЮЧЕНИЕ

Используя генератор изображений, содержащих примитивные геометрические фигуры, было выполнено обучение и дальнейшее тестировании модифицированной Mask R-CNN модели при различных сдвигах распределения параметров фигур и самого изображения. Обобщая проведенные эксперименты, можно выделить ряд ключевых наблюдений. Прежде всего, не все сдвиги распределения одинаково влияют на эффективность работы модели. Наибольшее влияние на точность сегментации оказывают сдвиги центра распределения, в то время как ширина сдвига либо не влияет вовсе, либо влияет слабо. Среди всех рассмотренных параметров наиболее чувствительными к сдвигу распределения оказались тон и яркость изображения. Изменение размеров фигур умеренно снижает точность сегментации. Сдвиг распределения насыщенности цвета, шума и степени наложения фигур практически не влияют на работу модели.

В дальнейших исследованиях эксперименты можно углубить за счет использования реальных изображений или изображений, сгенерированных нейросетью. Это позволит приблизить экспериментальные данные к фактическим, исключив особенности работы модели с простыми геометрическими фигурами.

Статья