Влияние шероховатостей поверхности диэлектрических микросфер на параметры формируемых фотонных наноструй

Изучение особенностей рассеяния света малыми частицами имеет важное значение при решении задач, направленных на совершенствование технологий дистанционного оптического зондирования [1, 2], обнаружения техногенных и природных аэрозолей [3, 4], прецизионной диагностики параметров дисперсных сред [5–7], микроскопии сверхвысокого разрешения [8] и т.д. В настоящее время также активно развиваются научные направления, связанные с наноструктурированием материалов при использовании микрочастиц в качестве оптических элементов, преобразующих падающее оптическое излучение [9, 10]. Здесь часто используют миниатюрные объекты различных геометрических форм (микропризмы [11], микроконусы [12], микрокубоиды [13]), однако наиболее востребованными с практической точки зрения по-прежнему остаются непоглощающие сферические диэлектрические микрочастицы. В большей степени это связано с более простой технологией изготовления микросфер с заданными размерами и внутренней структурой.

Обладая высокой степенью пространственной симметрии, сферические частицы с размерами поряд- ка длины волны падающего излучения (мезоволновые частицы) могут создавать в области ближнего поля протяженные локализованные световые потоки повышенной интенсивности – так называемые «фотонные наноструи» (ФНС) [14]. Пространственная форма и интенсивность ФНС оказываются чувствительными к изменению размера и оптических свойств микросферы [15–21]. Возможность управления параметрами фотонной наноструи, например, увеличение длины либо повышение пиковой интенсивности, делает эффект ФНС весьма привлекательным для множества практических приложений современной фотоники, в частности, спектроскопии высокого разрешения [14], нанолитографии [22], медицины (оптический скальпель или оптический пинцет) [23–25].

При численном моделировании эффекта ФНС, как правило, рассматривают частицы, имеющие идеальную сферическую поверхность. На практике же достичь подобной идеальности крайне сложно. Шероховатость существует почти на всех поверхностях природных частиц (кристаллы льда в перистых облаках, биологические споры в воздухе или воде, клетки тканей живых организмов), а также на искусственно изготовленных объектах [26]. Текстура поверхности рассеивающей частицы, помимо ее геометрической формы, является важным морфологическим фактором, определяющим оптические свойства рассеивателя. Любое, даже незначительное искажение поверхности, влечет за собой изменение характеристик светорассеяния частиц [27]. Однако, несмотря на важность обсуждаемой проблемы как с теоретической, так и с практической точек зрения, в настоящее время нет достаточной ясности в понимании специфики формирования ФНС при наличии шероховатостей поверхности микрочастицы.

Влияние шероховатости поверхности на рассеяние света в дальнем поле для частиц сферической формы было численно изучено в [28, 29]. Шероховатости задавались в форме псевдослучайных возмущений по сферическим углам, а исследовалась матрица рассеяния. Было показано, что в ряде случаев использование приближения идеальной сферы для шероховатых частиц может привести к заметным ошибкам в коэффициентах матрицы Мюллера.

В работах [30, 31] с помощью метода спектральных элементов исследовались специфические деформации диэлектрических микроцилиндров, в которых деформации вызываются с помощью гофрирования поверхности. Обнаружено, что с точки зрения ближнепольной микрофокусировки оптического поля, при определенных условиях гофрированные цилиндрические частицы могут проявлять себя так же, как и идеально гладкие микроцилиндры, обеспечивая высокую степень подъема интенсивности поля и появление типичных фотонных наноструй.

В настоящей работе, в отличие от предыдущих исследований, рассматривается ситуация, которая наиболее близко соответствует условиям экспериментов с фотонными наноструями, получаемыми от реальных микрочастиц. В нашем моделировании задаются не детерминированные искажения поверхности микросфер (эллиптичность, асферичность, регулярный гофр), а шероховатости считаются случайными (в рамках алгоритма машинного генератора случайных чисел) по всей координатной поверхности. По нашим сведениям, это одно из первых подобных исследований, выполненное для случая нерезонансной фокусировки оптической волны неидеальной диэлектрической микросферой, в котором систематически изучаются все значимые параметры ближнепольной фокальной области, существующей в виде ФНС. Мы показываем, что все характеристики ФНС могут существенно изменяться при возникновении искажений поверхности частицы, при этом две из них – интенсивность и продольная протяженность, являются наиболее чувствительными.

1.    Компьютерная модель диэлектрической микросферы с шероховатой поверхностью

Далее для определенности будем рассматривать рассеяние оптического излучения с длиной волны X =500 нм на непоглощающих сферических частицах радиуса R = 1 мкм. Поверхностная шероховатость ^ (x, у) генерируется с помощью стандартного алгоритма для создания случайной поверхности в спектральной области (включен в состав используемого программного пакета FDTD-расчетов). Этот алгоритм был нами адаптирован для конкретной задачи фокусировки поля на шероховатых микросферах.

Процедура состоит из нескольких шагов. Сначала инициируется матрица случайных равномерно распределенных комплексных чисел на плоскости декартовых координат ^ ( x , у ). Затем в 2D-пространстве Фурье-гармоник to _K={ to x , to y }, определяемом размерными параметрами численной сетки, задается Гауссовская корреляционная функция:

{ ^( x , у ) ^ ( x + 5 x , у + 5 у )^ -

- О ² exp { - ( to x L cx ) ² - ( to L ) ² } ,

где введены корреляционные длины L cx и L cy по координатным осям и амплитуда возмущений О . После этого в алгоритме используется спектральное преобразование Фурье для преобразования матрицы случайных частот обратно в реальное пространство. Вследствие особенностей работы быстрого преобразования Фурье, матрица шероховатости будет периодической с периодом численной сетки.

Наконец, вычисленная матрица шероховатостей с корреляцией (1) «обертывается» вокруг заданной геометрической фигуры (сфера) путем прибавления массива заранее вычисленных для сферической поверхности высот z0 - R2 -(x2 + у2) . Это приводит к возмущению всех точек по поверхности сферы радиусом R и созданию непрерывной шаровой структуры со случайной шероховатой поверхностью R (x, у) = zо (x, у) + ^(x, у).

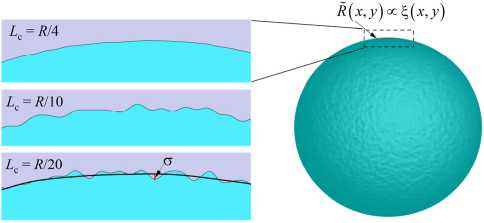
Рис. 1. Визуализация работы алгоритма задания шероховатости с амплитудой а и различной длиной корреляции возмущений Lc на сферической поверхности микрочастицы

В качестве иллюстрации работы данного алгоритма на рис. 1 показан участок поверхности частицы при различном значении длин пространственной корреляции возмущений. В дальнейшем для удобства анализа корреляционные длины возмущений по осям x и y будем считать равными, если не оговорено обратное. Поэтому дистанция корреляции поверхност- ных возмущений будет обозначаться одним символом: Lcx =Lcy =Lc .

2.    Результаты численного моделирования и их обсуждение

Численные расчеты проводились путем решения системы дифференциальных уравнений Максвелла для векторов электромагнитного поля ( E - H ) в 3D-координатном пространстве. Для этого использовалась стандартная технология конечно-разностной аппроксимации полевых переменных во временной области (FDTD), реализованная в коммерческом программном пакете Ansys Lumerical FDTD. Внутрь прямоугольной области, заполненной воздухом и окруженной идеально поглощающими слоями, реализующими выполнение условий свободного излучения поля через границы домена, помещалась диэлектрическая сфера со сгенерированной шероховатой поверхностью R ( x , y ).

В качестве источника оптического излучения задавалась плоская линейно поляризованная волна с длиной волны X, распространяющаяся с нижней стороны счетного домена в направлении оси z. Дискретизация пространства проводилась штатным сеточным генератором Lumerical при задании адаптивного алгоритма с минимальным шагом сетки в пределах микрочастицы 5 нм (X/100), что существенно меньше рассматриваемых здесь длин корреляции возмущений, и временным шагом порядка 0,02 фс.

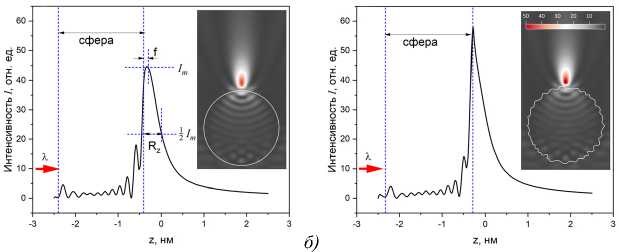
В результате рассеяния оптической волны на частице в ближнем поле формируется область фокусировки – ФНС, которая обычно характеризуется четырьмя пространственными (длина R z , полуширина по осям x и y – R x и R y , фокусное расстояние – f ) и одним амплитудным (фактор подъема интенсивности – I m ) параметрами. Принцип вычисления данных параметров показан на рис. 2 а и основан на анализе одномерных профилей относительной интенсивности оптического поля, получаемых при сечении 3D-распределения интенсивности поля I ( x , y , z ) в точке абсолютного максимума I m .

а)

Рис. 2. Примеры распределения относительной интенсивности I оптического поля в области ФНС от (a) идеальной и (б) шероховатой кварцевых сфер (п = 1,45), освещенных оптическим излучением ( Л = 500 нм).

Направление падения волны показано красными стрелками, а границы частицы – синим пунктиром

Показатель преломления вещества частицы n считался действительным числом (поглощения нет) и мог варьироваться. Для обеспечения репрезентативной статистики результатов для каждого набора входных переменных ( п , L c , о ) производился многократный расчет структуры оптических полей, каждый раз со случайно сгенерированной формой поверхности. Глубина выборки составляла 50 реализаций, в рамках каждой из них вычислялись значения параметров ФНС ( I m , f , R x , R y , R z ), и затем проводилось их математическое усреднение.

Сравнение рис. 2а и 2б показывает, что наличие шероховатости поверхности сферы приводит к изменению не только пространственного размера, но и интенсивности ФНС. Для заданных параметров расчета изменение текстуры поверхности сферы влечет сокращение протяженности струи, при этом в ряде случаев может наблюдаться повышение пиковой интенсивности Im, но в целом она снижается. Численные расчеты также показали, что координата максимума интенсивности фотонного потока f для идеальной сферы (рис. 2а) удалена от поверхности, в отличие от случая частицы с шероховатой поверхностью на рис. 2б, когда фокусное расстояние f =0, а поле в области внешнего фокуса формируется в виде экспоненциально затухающего (эванесцентного) «хвоста».

Далее более подробно обсудим обозначенные выше размерные характеристики фотонных наноструй от частиц с различными типами искажений поверхности.

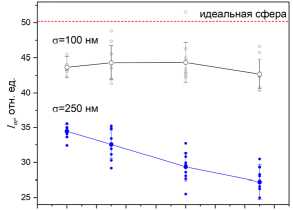
На рис. 3 а-б представлены зависимости пиковой интенсивности I m (рис. 3 а ) и длины R z струи (рис. 3 б ) от длины корреляции возмущений L c шероховатостей поверхности микросферы. Расчет проведен для двух значений амплитудного параметра о (по х и у ): о = 100 нм и 250 нм. Точки на графиках получены в результате усреднения по 50 реализациям. Отмечен также доверительный интервал разброса значений параметров.

Видно, что параметры фотонной наноструи от микросферы с шероховатой поверхностью существенно отличаются от своего «идеального» аналога (на рисунках соответствующие значения Im и Rz обозначены как «идеальная сфера»). Оба рассмотренных параметра ФНС уменьшаются. В то же время при невысокой амплитуде шероховатостей (о =100 нм = X/5) изменение длины их пространственной корреляции в рамках статистической вариации практически не влияет ни на интенсивность ФНС, ни на ее длину. Увеличение степени шероховатости поверхности (о = 250 нм) приводит к заметному падению пиковой интенсивности струи (до двух раз при Lc >150 нм) и сокращению ее длины вследствие затягивания оптического поля внутрь частицы при микрофокусировке на шероховатостях. При этом более плавные возмущения поверхности (параметр Lc растет) оказывают большее влияние на характеристики фотонной струи. Что касается пространственных размеров струи в поперечном направлении (не показано), значимого влияния длины корреляции шероховатости частицы на параметры Rх, Ry выявлено не было.

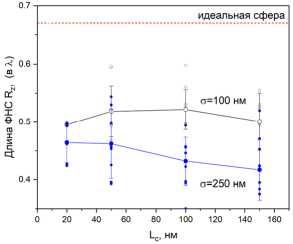
Далее обсудим серию графиков (рис. 4 а, б ), представляющих результаты численного моделирования зависимости пиковой интенсивности (рис. 4 а ), длины и ширины ФНС (рис. 4 б ) от другого расчетного параметра, а именно, амплитуды возмущений о . Как было установлено выше, интенсивность ФНС заметно падает при возрастании амплитуды неоднородностей поверхности. Эта зависимость представлена на рис. 4 а для трех различных значений пространственного масштаба корреляции шероховатостей. Видно, что указанная тенденция сохраняется при любых размерах неоднородностей, причем начиная со значений L c > 100 нм = λ /5 интен-

Рис. 3. Зависимость пиковой интенсивности ФНС I m (а) и протяженности R z (б) от длины корреляции искажений поверхности микросферы L c

О 20    40    60    80   100   120   140   160

а)                                          б)

сивность ФНС уже перестает зависеть от масштаба шероховатостей и «чувствует» только их амплитуду.

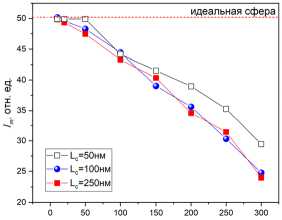
Интегральная оценка пространственных размеров струи может быть дана только на основании комплексного анализа всех ее размерных параметров, а именно, длины R z и полуширин по координатным осям x и y ( R x , R y ). На рис. 4 б представлены результаты численного расчета данных величин для выбранного значения корреляции поверхностных возмущений L c =250 нм. Здесь же для сравнения представлены соответствующие значения для идеальной сферы. Видно, что с увеличением о для частиц с шероховатой текстурой поверхности уменьшается длина струи R z (синяя кривая) и ее поперечный размер по оси x – R x (черная кривая), что свидетельствует о формировании локально ограниченного ближнепольного фокуса. В то же время происходит рост другого поперечного размера R y (красная кривая), а следовательно, уширение фотонного потока в поперечном к плоскости поляризации направлении (по оси y ) . Таким образом, при сильной шероховатости поверхности фотонная наноструя теряет свою изначальную эллипсоидальную форму, которая характерна для случая облучения сферы линейно поляризованной волной, и приобретает пространственный вид квазикругового конуса с основанием у поверхности микросферы.

а)

б)

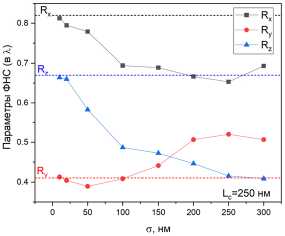
Рис. 4. Зависимость пиковой интенсивности I m (а) и длины R z (б) ФНС от амплитуды а искажений поверхности микросферы. Пунктирные линии – соответствующие значения для идеальной сферы

Представленные выше расчеты проведены для шероховатых сфер, изготовленных из материала, близкого по показателю преломления к обычному кварцевому стеклу с n = 1,45. Ниже рассмотрим более широкий ряд значений n и обсудим влияние шероховатости поверхности микросфер на их оптические свойства. В качестве модельной частицы была выбрана микросфера с параметрами шероховатости Lc = 100 нм и о = 100 нм. Сравнение проведено с идеально сферической частицей того же радиуса и оптических свойств (рис. 5 и 6).

Из анализа рис. 5 следует, что изменение показателя преломления частицы позволяет управлять интенсивностью ФНС. В первую очередь, обращает на себя внимание подобие кривых для идеальной сферы и сферы с шероховатой поверхностью, а также наличие явно выраженного пика при n = 1,6, когда фотонная струя имеет максимум точно на теневой поверхности сферы [32]. Интересно, что для водных частиц (n = 1,33) заданные при численном моделировании параметры шероховатостей не изменяют мощностных характеристик ФНС, поскольку в этом случае наноструя достаточно далеко отстоит от частицы (см. рис. 6г) и не «чувствует» рельефа ее поверхности. При этом для частиц с показателем преломления n > 1,6 отличие в значениях Im уже становится существенным и может превышать ~ 100%.

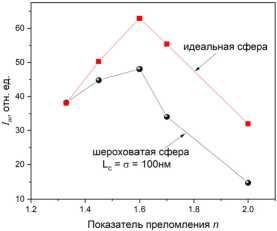
Рис. 5. Зависимость пиковой интенсивности фотонной наноструи Im от показателя преломления рассеивающей частицы n для идеальной сферы и сферы с шероховатостью поверхности

Показатель преломления п

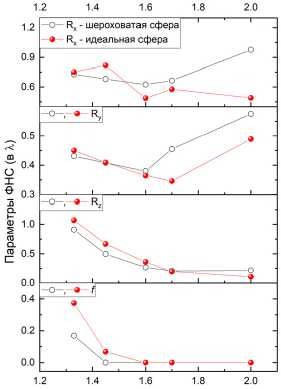
Рис. 6. Пространственные размеры фокальной перетяжки при изменении показателя преломления n рассеивающей частицы при L c = 100 нм и σ = 100 нм

Пространственный размер ФНС также чувствителен к изменению показателя преломления рассеивающей излучение частицы (рис. 6). Как показали наши расчеты, в направлении плоскости поляризации (вдоль оси x) и поперек поляризации волны (вдоль оси y) пространственный размер фокуса Rx и Ry увеличивается в диапазоне значений от n = 1,6 до 2, т.е. происходит уширение пятна фокусировки. Продольный размер фокальной области Rz характеризуется более сглаженной зависимостью от n и не имеет явно выраженных максимумов. Более того, длина ФНС практически не зависит от качества поверхности сферы. Увеличение показателя преломления сферической частицы приводит к постепенному сокращению длины струи, что связано с обострением фокусировки при повышении отношения показателей преломления сферы и окружающей среды (воздуха).

Удаленность максимума интенсивности ФНС от поверхности рассеивающего излучение объекта определяется параметром фокусного расстояния f (рис. 6 г ). Видно, что при n > 1,6 для идеальной сферы (красная кривая) фотонная струя всегда имеет максимум интенсивности на поверхности частицы, в то время как для искаженной сферы (черная кривая) эта ситуация реализуется уже для n > 1,45. При этом отличие значений f для сферической и волнистой водных частиц ( n = 1,33) составляет порядка двух раз.

Следует заметить, что реализовать искажения поверхности, подобные показанным на рис. 1, в жидких частицах (каплях) возможно только в динамике, т.е. возбудив поверхностные колебания, например, переменным воздушным потоком, или за счет неоднородного распределения температуры (термокапиллярные деформации), или интенсивным оптическим полем за счет действия пондеромоторных сил [33].

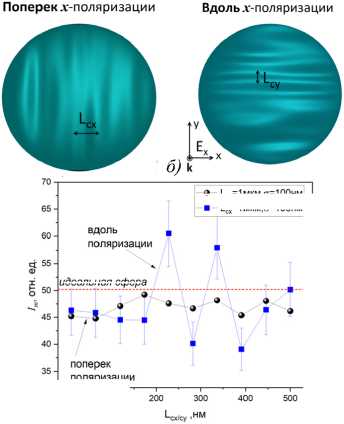
Все представленные выше результаты получены для случая симметричных возмущений по осям x и y . Рассмотрим теперь вариант резко несимметричных искажений поверхности диэлектрической частицы, когда выполняется неравенство: L cx ^ L cy . Напомним, что в качестве оптического источника, освещающего микросферу, используется плоская линейно поляризованная по оси x волна. Следовательно, при создании возмущений поверхности сферы преимущественно вдоль или поперек вектора поляризации поля возможно ожидать различный эффект на параметры возникающей фотонной струи. В рамках используемого алгоритма генерации случайных возмущений пространственная асимметрия шероховатостей по осям x и y создавалась путем задания соответствующего параметра длины корреляции ( L cx или L cy ) на фиксированном уровне, равным для определенности радиусу сферы, и вариации другого оставшегося параметра. В результате, на поверхности сферической частицы возникал рельеф неоднородностей вдоль одной из координатных осей (см. рис. 7 а и б ).

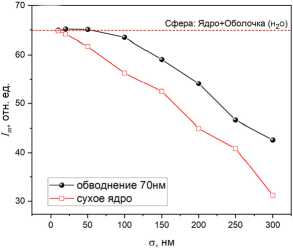
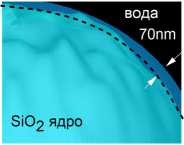
Результаты расчетов интенсивности ФНС показаны на рис. 7в. Видно, что случаи резкого изменения амплитуды шероховатостей преимущественно вдоль или поперек вектора поляризации волны оказывают разное влияние на параметр Im. Особенно это заметно в диапазоне длин корреляции возмущений, примерно X/2

а)

идеальная сфера

в)

Рис. 7. Схематическое изображение поверхности частицы при создании возмущений поверхности (а) поперек и (б) вдоль поляризации плоской волны. (в) Интенсивность ФНС Im в зависимости от корреляционной длины поляризации

в Ьсу=1мкм,а=100нм

Lc,=1mkm,g=100hm асимметричных шероховатостей

Если же микрорельеф образован поперек поляризации оптического поля (рис. 7а), то никаких протяженных микролинз на поверхности частицы для компоненты поля Ex не образуется. Независимо от периода пульсаций формы поверхности вдоль x, интенсивность ФНС лишь незначительно снижается, в среднем на 10%. Размерные параметры фотонной струи ведут себя подобным образом, испытывая наибольшие изменения для случая продольного расположения гофрированного микрорельефа.

Интересно обсудить также возможности снижения влияния шероховатостей поверхности микросфер на качество фокусировки ближнего оптического поля. В качестве одного из таких способов, не связанных с вмешательством в технологию изготовления микрочастиц, можно предложить покрытие частиц каким-либо жидкофазным материалом, который заполняет все микронеоднородности твердой поверхности и за счет сил поверхностного натяжения создает близкую к идеальной двуслойную сферу. Тогда все локальные фокусировки оптического поля, возникающие на неоднородностях твердого ядра, сглаживаются внешней сферической поверхностью. Простейшим вариантом здесь является обводнение микрочастиц, т.е. создание водной наноразмерной пленки на их поверхности.

Указанная ситуация моделировалась нами путем создания двухслойной частицы, состоящей из кремниевого ядра с шероховатой поверхностью и внешней сферической водной оболочки толщиной dw =70 нм (n = 1,33). Результаты расчетов интенсивности ФНС Im приведены на рис. 8. Для сравнения здесь также приведена зависимость данного параметра для сухой микросферы того же внешнего радиуса Rw = R + dw с шероховатостями поверхности. Для упрощения анализа длина корреляции возмущений Lc в расчетах была неизменной и составляла 100 нм.

б)

а)

в)

Рис. 8. (a) Интенсивность ФНС в зависимости от амплитуды шероховатостей для сухой и обводненной кварцевых частиц (n = 1,45). Изображение части поверхности (б) сухой и (в) обводненной микросфер

Из данного рисунка видно, что до тех пор пока водная пленка способна заполнить микровпадины, т.е. примерно до значения амплитуды возмущений о = 2dw, шероховатость поверхности практически не сказывается на степени подъема интенсивности ближнего поля. Фазовый фронт оптической волны, искаженный микрофокусировками на выступах и впадинах твердой поверхности, сглаживается и «исправляется» гладкой внешней водной поверхностью. При дальнейшем росте амплитуды шероховатостей, аналогично сухой частице, интенсивность ФНС демонстрирует монотонное падение.

Заключение

Рассмотрены основные характеристики фотонных наноструй (пространственный размер, пиковая интенсивность), формирующихся в окрестности прозрачных диэлектрических микросфер микронного радиуса с различными типами случайно сгенерированных искажений поверхности при облучении их лазерным излучением с X = 500 нм. Детально исследованы случаи симметричных и несимметричных искажений поверхности частицы. Установлено различное влияние корреляционной длины и амплитуды возмущений поверхности на ключевые параметры ближнепольной фокальной области.

Численные расчеты, выполненные в рамках FDTD-метода, наглядно продемонстрировали, что наличие шероховатостей поверхности приводит к изменению фокусирующих свойств частицы по сравнению со своим «идеальным» аналогом. При этом наиболее восприимчивыми к изменению текстуры поверхности рассеивающей оптическое излучение частицы являются два параметра ФНС, а именно, пиковая интенсивность и ее протяженность в поперечном к поляризации волны направлении.

Изменение характеристик ФНС возможно также путем варьирования оптического контраста (относительного показателя преломления) рассеивающей излучение микросферы. Определен диапазон значений показателя преломления микросферы, в котором для заданных параметров модельной частицы происходит уширение пятна фокусировки, однако длина ФНС практически не зависит от качества поверхности сферы.

Предложена возможность снижения влияния шероховатостей поверхности на качество фокусировки ближнего оптического поля при обводнении микросфер.

Работа выполнена при поддержке Министерства науки и высшего образования в рамках выполнения работ по Государственному заданию ИОА СО РАН.