Влияние шума на вейвлет-спектр

Вейвлет-анализ является инструментом анализа динамики систем и привлекает в последнее время все больше внимание исследователей, нуждающихся в локальном анализе нестационарных сигналов [1, 2]. Локальный анализ требует анализа локальных особенностей вейвлет-спектра на малых масштабах, где влияние шумов относительно велико. Целью исследования является оценка влияния шумов на вейвлет-спектр и анализ их расположения.

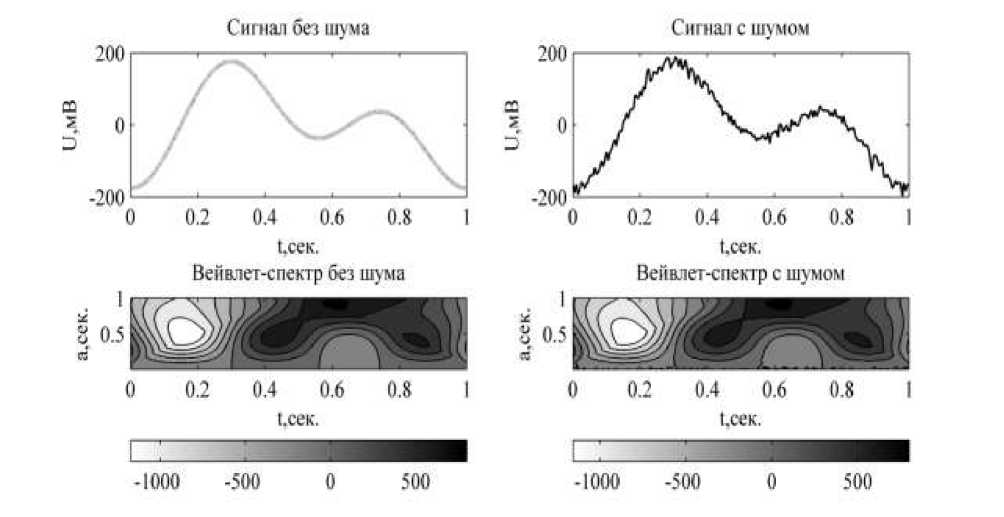
Рис. 1. Сумма синусоид и его вейвлет-спектр: (слева) без шума, (справа) с белым шумом

Методика исследования

На примере модельного сигнала, имеющего две особенности разных масштабов, проанализируем влияние шумов. Итак, рассмотрим модельную кривую с аддитивным белым шумом 5 100 sin(2ut —

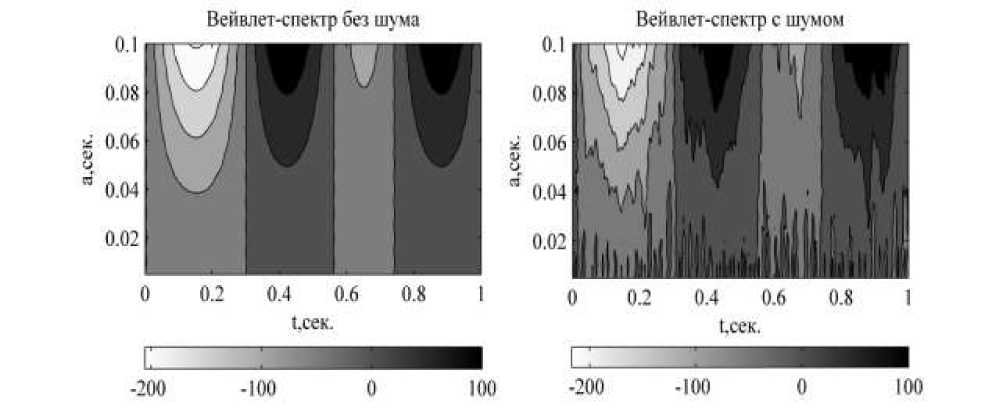
Рис. 2. Вейвлет-спектры на малых масштабах: (слева) без шума, (справа) с белым шумом

Для наглядности представим вейвлет-коэффициенты, соответствующие этим масштабам на одном графике (рис. 3). Видно, что шумы влияют на вид кривых на всех масштабах, представленных на графике справа. Амплитуды вейвлет-коэффициентов увеличиваются по мере возрастания масштабов, поэтому на графиках они имеют одну форму, но разную ам- плитуду.

Вей влет-ко эффнциенты без шума

2001-----------------------■-----------------------■-------

Вейвлет-коэффициенты с шумен

-100

Z D

-100

-200

-200

-300 L 0

0.4     0.6

1,сек.

-300 L 0

0.4     0.6

1,ССК.

Рис. 3. Вейвлет-коэффициенты на масштабах от 0,01 до 0,1 с: (слева) без шума, (справа) с белым шумом

Заметим, что при отсутствии шума положение точек экстремумов и нулевых точек, определяющих общий вид вейвлет-спектра, не меняются на данных масштабах. При наличии шума точки экстремумов и нулей могут иметь положение, не совпадающее с положением при отсутствии шума. Рассмотрим положение нулевых точек вейвлет-спектра сигнала без шума в сравнении с вейвлет-спектром при наличии шума. На рисунке 4 показаны вейвлет-коэффициенты вейвлет-спектра с шумом на масштабах от 0,01 до 0,05 с с обозначенными нулевыми точками из вейвлет-спектра сигнала без шума. Видно, что из-за наличия шума при малых масштабах (0,01-0,04 с) появляется большое количество точек экстремумов и нулевых точек, имеющих шумовое происхождение. Это значительно осложняет анализ локальных особенностей сигнала на малых масштабах вейвлет-спектра.

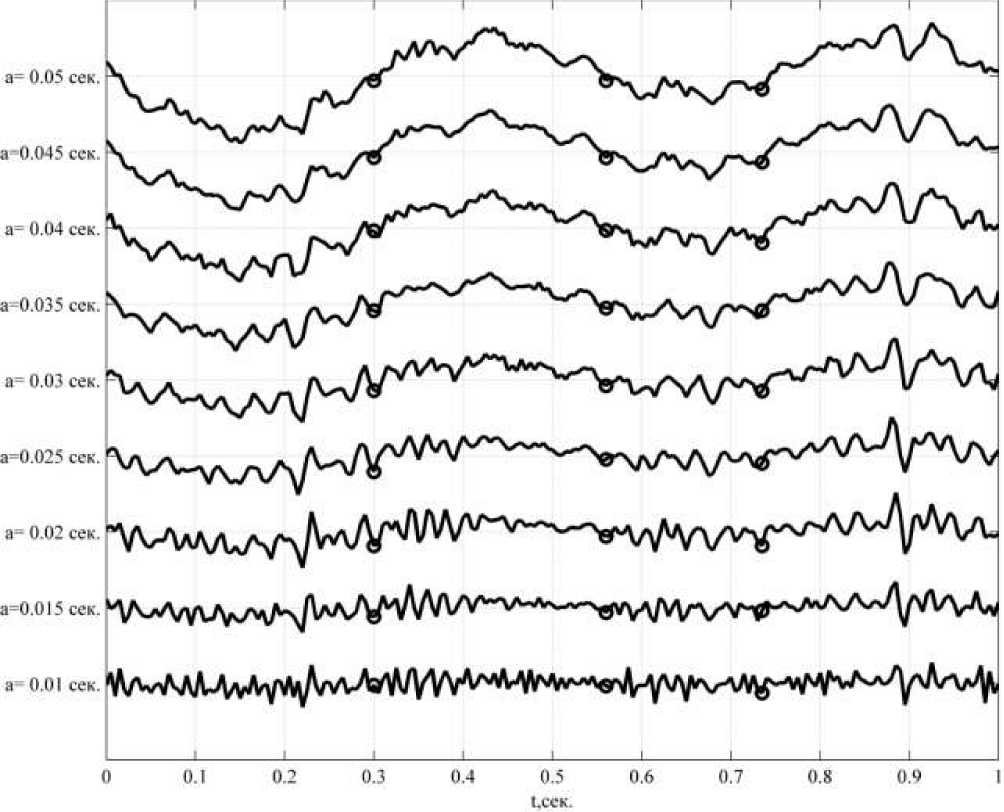
Рис. 4. Вейвлет-коэффициенты на масштабах от 0,01 до 0,05 с с вейвлет-спектра при наличии белого шума с обозначенными нулевыми точками из вейвлет-спектра без шума

При масштабах до 0,1 с разница координат нулевых точек колеблется. Начиная с масштаба 0,1 с координаты этих точек определяются так же, как при отсутствии шума. На рисунке 5 пунктирной линией показаны вейвлет-коэффициенты на масштабах 0,1, 0,2, 0,3 с при отсутствии шума, а сплошной линией - при наличии шума. Видно, что наличие шума влияет на гладкость вейвлет-коэффициентов на этих масштабах, при этом форма кривых сохраняется, и координаты нулевых точек и точек экстремумов совпадают с аналогичными координатами точек при отсутствии шума.

Заключение

Таким образом, анализ влияния шума на вейвлет-спектр показал, что шум существенно влияет на вейвлет-коэффициенты и вид вейвлет-спектра при малых масштабах. Это влияние добавляет на вейвлет-спектре множество локальных особенностей, имеющих шумовое происхождение. Следовательно, при подробном анализе и поиске локальных особенностей и закономерностей на вейвлет-спектрах следует учитывать наличие помех и выбирать для ана- лиза масштабы, где влияние шума незначительно. На наименьший масштаб без шумовой составляющей будет влиять уровень шума чем он выше, тем больший надо выбирать масштаб. Данные рекомендации будут полезны при анализе экспериментальных сигналов с наличием помех, каковыми являются большинство биологических и технических сигналов.

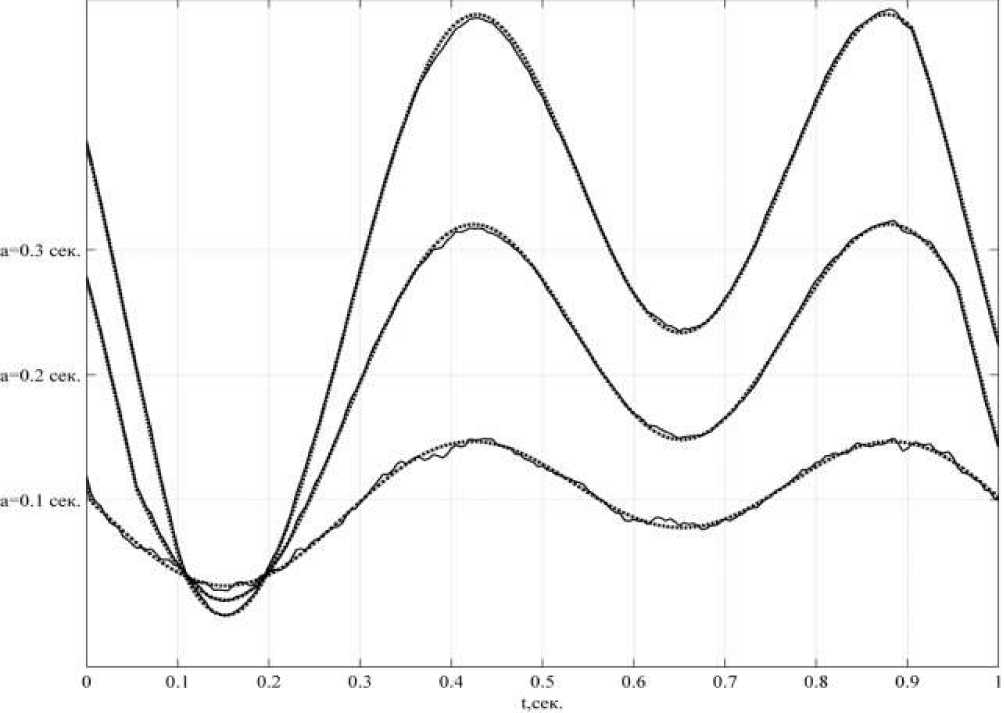
Рис. 5. Вейвлет-коэффициенты на масштабах 0,1, 0,2, 0,3 с (пунктирная линия) без шума, (сплошная линия) с белым шумом