Влияние слоистых неоднородностей тропосферы на дифракционное поле УКВ

Введение. На закрытых приземных трассах основными механизмами распространения УКВ являются дифракция вокруг земной поверхности [1-5] и переизлучение волн неоднородностями диэлектрической проницаемости тропосферы [1,2]. Для частотно-территориального планирования радиосетей различного назначения необходимы модели, учитывающие эти механизмы. Как правило, влияние земной поверхности и тропосферных неоднородностей, при расчете загоризонтного распространения, учитывается раздельно. Между тем очевидно, что наиболее адекватным реальной ситуации должен являться совместный учет влияния обоих механизмов распространения. Это особенно относится к промежуточной зоне теневой области, где дифракционная и тропосферная компоненты соизмеримы по амплитуде и их интерференция может приводить к аномально высоким уровням поля, вызывающим ухудшение условий электромагнитной совместимости радиосредств, и к глубоким замираниям сигнала.

В качестве простой модели совместного учета дифракционного и тропосферного механизма в данной работе рассматривается задача о распространении радиоволн на трассе с клиновидным препятствием, когда над ним находится отражающий тропосферный слой.

Теория. Пусть между источником А сферической волны и точкой наблюдения Р находится клиновидное непрозрачное препятствие, над которым расположен отражающий тропосферный слой (рис. 1)/ Будем полагать, что удаления источника, края препятствия и приемника от границы раздела много больше длины волны. Тогда для решения задачи можно воспользоваться методами геометрической оптики (ГО) и геометрической теории дифракции (ГТД) [7, 8].

На рис. 1 показаны геометрооптические и дифракционные лучи, возникающие в данной задаче. Результирующее поле в точке, согласно ГТД и ГО, имеет вид:

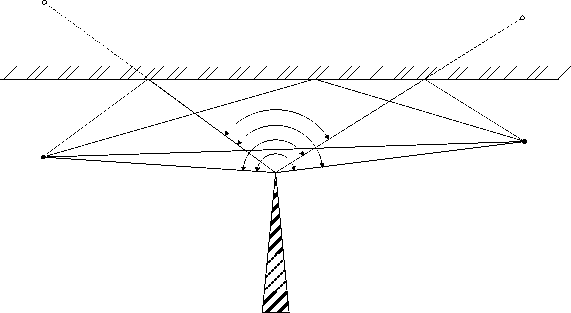
Рис. 1. Геометрия задачи

U№=Ms-«yU^-a_x\^    +U₅₆₁ + Г₄₈₉ + Г₅₆₈₉ ,         (1)

где л v 7 - единичная функция Хевисайда, индексы показывают последовательный путь лучей.

Выражения для полей, входящих в формулу (1), получены с помощью методов ГО и ГТД. Например, поле U561 имеет вид ехр[^(г5+г6+г7)] Г тг 2к(г5+г6)Г1

>1Цг5 +r6 +r7)     ( 4    r5+r6+r7      2 J ^ r5+r6 + r7 2 J где Д] - коэффициент отражения луча 5 от границы слоя.

Численные результаты. Для оценки влияния тропосферного слоя были проведены расчеты множителя ослабления поля V=U(P)/Ui для случая, когда слой представляет собой полупространство, т.е. отражающей поверхностью является граница раздела двух полупространств с диэлектрическими проницаемостями е = 1 + v, e=l+v + Jec |Je| < v « 1, где Л с - скачок диэлектрической проницаемости на границе раздела, который может иметь как положительный, так и отрицательный знак. В этом случае коэффициент отражения от слоя независимо от поляризации волны описывается формулой sin а - Vas + sin2 а sin а + Vas + sin2 а где а - угол скольжения волны.

Расчеты проведены для различных длин трасс, высот препятствия, их расположений на трассе и различных значений скачков диэлектрической проницаемости. Для примера на рисунке 2 приведены результаты расчета для трассы длиной 50 км и клиновидным препятствием, расположенным посередине трассы. Результаты получены при различных значениях высоты препятствия Н над линией АР в зависимости от расстояния между границей раздела и краем препятствия Н, на длине волны 2=10 см.

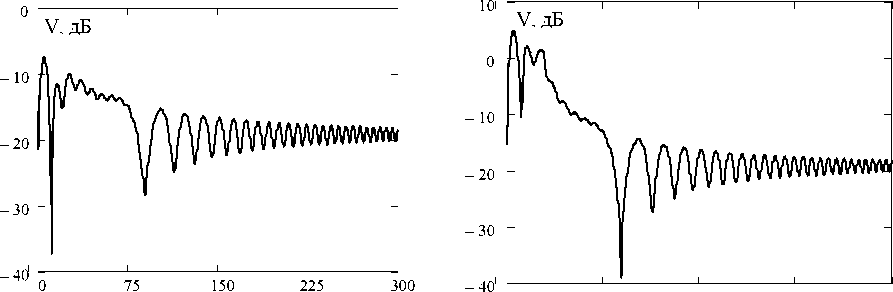
а)                                                           б)

Рис. 2. Зависимости множителя ослабления от высоты слоя над краем препятствия а) Н = 50 м, Ле = 10"5, б) Н = 100 м., Ле = - 10"5

Приведенные зависимости показывают, что интерференция дифракционного поля и поля, отраженного от тропосферного слоя, при определенных соотношениях между геометрией трассы, длиной волны, параметрах слоя могут приводить к значительным изменениям уровня результирующего сигнала.