Влияние смазочно-охлаждающих технологических средств на теплообмен в зоне контакта при разрезании заготовок из пкм отрезными алмазными кругами

Как было установлено ранее [1, 2] величина плотности теплового потока q_c при разрезании заготовок алмазными отрезными кругами на разных отрезках режущей кромки определяется кинематическими параметрами процесса и температурой, распределенной по длине дуги контакта режущей кромки с заготовкой.

Поверхностная плотность теплового потока q _ж, отводящего из зоны контакта тепло на нагрев и парообразование смазочно-охлаждающей жидкости (СОЖ), определяется зависимостью [1]:

f c G ( t - T ,)

ж ж \ f ' T с' T

—, T ^ T f ^;

^G ж = G жт ⁺ G жц = Р ж (V жт ⁺ V жц ), (2) где G _жт , G _жц – соответственно массовый расход СОЖ, уносимой торцевой и цилиндрической поверхностями режущей кромки, кг/с;

V _жт, V _жц – соответственно объём СОЖ, уносимой торцевой и цилиндрической поверхностью режущей кромки в единицу времени, м³/с.

Объём СОЖ, уносимой торцевой поверхностью режущей кромки V _жт при отсутствии фазового перехода находится по [3]:

V™ = I ^П ( d pk 1 - d pk 2 Xl - £ pk 3 ) ( 1 - ^KV ) ^X 3 n , (3)

q ^ = I

S

c_n ^ G_n ^ T - ^Tf ⁾⁺ c , G , T - T f ) _{T T} , T >  T f ,

где d²_pk1 d²_pk2 – соответственно наружный и внутренний диаметры режущей кромки отрезного

S

где G_ж , G_пж = c_жG_ж(T – T_f )/r – соответственно массовый расход СОЖ в парообразном и жидком состоянии проходящей через зону контакта круга и заготовки, кг/с;

r – удельная теплота парообразования СОЖ, Дж/кг;

Т – температура насыщения СОЖ, К;

Т _f – температура потока СОЖ, К;

c_ж – теплоемкость СОЖ, Дж/(кгК);

G_ж = ρ _жV_ж , где ρ _ж – плотность СОЖ, кг/м³;

V _ж – объём СОЖ, уносимой алмазоносным слоем режущей кромки круга через зону контакта в единицу времени, м³/с.

S – площадь контакта режущей кромки с заготовкой, м2

алмазного круга;

h k^p 3

^ рз = "⁼⁼" — относительная критическая

³    X з

глубина заделки алмазных зёрен в связке;

• h_kp3 – критическая глубина заделки алмазных зе рен, м;

• X ₃ – средневероятный размер алмазных зерен, м;

K_V – коэффициент, учитывающий объём, занимаемый алмазными зёрнами, выступающи-

ми из связки;

n – частота вращения круга, с^–1;

KV

^Vl 3 ^NS X 3

где V_l3 = 1/(4N_l ) – объём единичного алмазного зерна, м³;

N_l – количество алмазных зёрен в единице объёма, шт./м³;

N S - число алмазных зёрен на поверхности круга, шт. [4, табл. 9].

Аналогично (3) запишем объём СОЖ V жц , уносимый цилиндрической поверхностью режущей кромки круга:

V ., = « W- pk ( 1 - е„ , ) ( 1 - KV ) X , . . (5)

Следовательно, подставив (3) и (5) в (2), получим:

G»■ = Р^п (1 — Ерк з )(1 — Kv )х ^.          ^.               pk 3

---- [ d 2,, - d хX3n — p + dpk 2hpk . (6) к 2

Рассчитаем местные коэффициенты теплоотдачи со свободных поверхностей круглой заготовки а з или отрезаемой пластины а _пл, режущей кромки a_pk и корпуса отрезного круга а_к (см. [2]). Соответствующая геометрия задана ранее (см. [2]).

Используем эмпирическими уравнениями подобия [5].

Участок АВ круга (см. рис. 1) рассмотрим как участок заготовки, продольно обтекаемой потоком СОЖ с относительной скоростью:

потоком можно определить по эмпирическому уравнению подобия [5]:

_____                    [ р_г к ^0,25

NUf = ^0,66Re 0 ^^рг f ’⁴³[- f ] .    (9)

к w )

где NUT_f = "' B ; Р-_Л _ uC f- ;

ff

Л к f            Л к f

^Uw^C K w .   „  _   ^{0 AB}

“          ’ f ^,

Лк w          Vf apk - среднее на участке АВ значение коэффициента теплоотдачи, Вт/(м2К).

К ж - теплопроводность жидкости, Вт/(м К).

Параметрам, выбираемым по температуре СОЖ на выходе из насадка, присвоим в обозначениях индекс f. Параметрам, выбираемым по средней температуре поверхности режущей кромки на участке АВ - индекс w .

Если Re > 10^s , то расчёт ведут по эмпирическому уравнению подобия для турбулентного режима течения:

Nu f = 0,0296RefPr f’⁴³

f ^ Г

I Pr w J

.

u о = to r pk ^- u . COS «_v ⁽⁷⁾

где и ж =д ж /S c скорость истечения СОЖ из насадка, м/с;

g _ж - объёмный расход СОЖ из насадка, м³/с;

S_c - площадь выходного сечения насадка , м². Определим число Рейнольдса:

Re _ u 0 l AB _ P . u 0 l AB

^V 1         Р 1

где l_AB - длина участка AB , м;

v 1 , ц 1 - соответственно кинематический и динамический коэффициент вязкости СОЖ, Па-с.

По аналогии, расчётную схему для определения коэффициента теплоотдачи от корпуса отрезного алмазного круга к СОЖ при Re ^ 10^s можно получить при обтекании заготовки, ламинарным потоком по эмпирическому уравнению подобия:

_____                      f p_r k ^0,25

Nu f = ^0,66R e 0^^p r 7³- f   ,   (11)

< ^pr w J

где

Nu f

^a k l AB      =

^/    f

^ж /

^U f ^C ж f .

^ f ^ж /"

Если Re ^ 10^s , то коэффициент теплоотдачи в условиях обтекания заготовки ламинарным

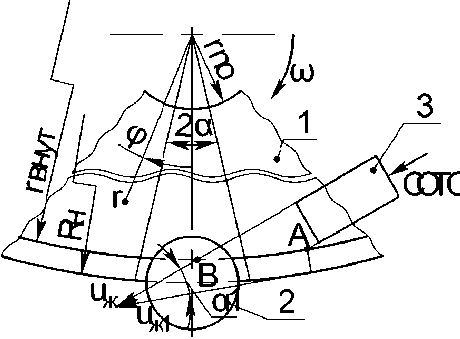
Рис. 1. Расчётная схема для определения коэффициентов теплоотдачи:

1 - корпус отрезного круга; 2 - заготовка;

3 -насадок для подачи СОЖ

pr

w

и C u w ^ ж w . Re ’

^ ж w

u 0 l AB

f vf

a _k - среднее на участке АВ значение коэффициента теплоотдачи от круга к СОЖ, Вт/(м²К).

Если Re > 10^s (турбулентный режим течения), то

_____                         f p_r k ^0,25

Nu_f = 0,0296Re ^0o,8 Pr 0^,43 -f    . (12)

1              1    1 I prw J

Расчётную схему для определения коэффициента теплоотдачи от заготовки к СОЖ принимаем для случая поперечного обтекания цилин-

дра. Значение коэффициента теплоотдачи а _з , среднее по поверхности заготовки, обтекаемой СОЖ, определим по эмпирическому уравнению подобия [4]:

Nu f

= C • Re ^m d Pr ^m

f1125

Pr

V Prw 7

,

кромки, зависящий от скорости выхода аэрозоля из насадка.

В этом случае:

W^ d где Prfd =---, Nuf = -г—-, C, m, n - числовые

Vf           кжf коэффициенты, выбираемые в зависимости от диапазона числа Re fd в соответствии со следующей таблицей.

Таблица 1. Числовые коэффициенты

Gж = ^ Q«k_c .          (18)

^ж       ^ж a c

Re fd	C	m	n
5÷103	0,5	0,5	0,38
> 103	0,25	0,6	0,43

При подаче аэрозоля получаем следующие зависимости.

Участок АВ круга (см. рис. 2) принимаем как участок заготовки, продольно обтекаемой струей аэрозоля со скоростью u₀ :

u 0 = to r pk ± u ж ,              (19)

Для определения коэффициента т еп лоотдачи от отрезаемой заготовки к СОЖ ^ , рассмотрим продольное обтекание заготовки по участку АВ, меняющему своё положение в процессе разрезания. При этом скорость потока находится по зависимости:

u 0 = K ж ^ЮГ рк + u ж. ^C0S « 1 , (14)

где uж = gж /Sc – скорость истечения аэрозоля из насадка, м/с, gж – объёмный расход аэрозоля из насадка, м3/с;

S_c – площадь выходного сечения насадка, м².

Окружная скорость отрезного круга меньше скорости истечения аэрозоля [6], из-за чего полагаем u₀ = u_ж .

Определим число Рейнольдса:

= u 0 l AB = Р ж^и 0 l AB

^V 2        ^ 2

где Кж – коэффициент, учитывающий разгон жидкости корпусом отрезного круга.

Коэффициент теплоотдачи от отрезаемой плоской заготовки-пластины к СОЖ при Re ≤ 105 можно получить аналогично в условиях обтекания заготовки ламинарным потоком по эмпирическому уравнению подобия:

_____                      f P_r 1 ^0,25

Nu_f = 0,06 • Re^Pr® ’⁴³ -f    ,   (15)

где                     J J V Pr. 7

где l_AB – длина дуги АВ, м;

ν ₂ , μ ₂ – соответственно кинематический и динамический коэффициент вязкости распыляемой жидкости, Па·с.

Nu ff =

^ пл l AB

2 _f ж f

^Pr f =

^ f^C ж f .

k ж/

MwCж w rw кж w

Re _f =

u 0 l AB

^V f

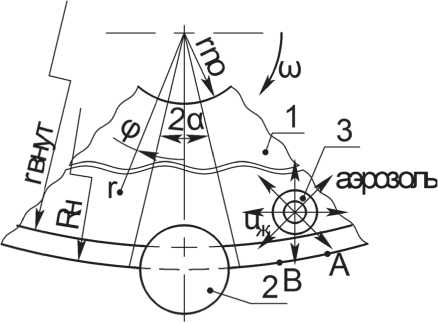
Рис. 2. Расчётная схема для определения коэффициентов теплоотдачи:

1 – корпус отрезного круга; 2 – заготовка;

3 – сопло для подачи аэрозоля

а _ил - среднее на участке АВ значение коэффициента теплоотдачи от отрезаемой заготовки к СОЖ, Вт/(м²К).

Если Re > 10 ⁵ (турбулентный режим течения), то:

_____                         f P_r 1 ^0,25

Nu_f = 0,0361 • Re ⁰;⁸ Pr ?’⁴³           . (16)

f       ff

V P1w 7

При использовании вместо СОЖ аэрозоля, применение которого все более увеличивается [6], объём жидкости, уносимый алмазоносным слоем режущей кромки через зону контакта в единицу времени, определяется по формуле:

^Vж = Q a k c , (17)

Параметрам, выбираемым по температуре СОЖ на выходе из сопла, присвоим в обозначениях индекс f , как и в случае с обтеканием ламинарным потоком. Параметрам, выбираемым по средней температуре поверхности режущей кромки на участке АВ – индекс w .

Рассчитываем по эмпирическому уравнению подобия, полученному для турбулентного

где Q_a – расход аэрозоля, м³/с;

k_c – коэффициент смачиваемости режущей

режима течения:

_____                          f P_r 1 ^0,25

Nu_f = 0,0296 • Re °;⁸ Pr 0,⁴³ -f    , (21)

f        ff

V P1^ 7

где Nu f - ^ ^ l AB- ; Pr _f - ff ; A k f            A k f

Pr = MwCm rw       j

^A kw

_{Re f} - u A B , ^v f

a_m - среднее на участке CD значение коэффициента теплоотдачи от отрезаемой плоской заготовки-пластины, к СОЖ, Вт/(м²К).

Проанализируем далее воздушное охлаждение.

Исследования [8], показали, что формирование воздушных потоков у отрезного круга начинается от планшайбы. Наиболее мощные потоки генерируются торцами алмазного круга. Наличие пор у абразивных кругов позволяет им достичь избыточного давления воздуха на периферии 0,03-0,05 МПа. Избыточное давление воздуха на режущей кромке алмазного круга можно считать близким к нулю. Поэтому примем, что теплоотдача к воздуху в процессе разрезания происходит за счёт свободного теплообмена.

Определим соответствующие коэффициенты теплоотдачи [4]:

a

св

Nu Я mm d 3

Определяющая температура:

гр __ ¹ B ' ¹ pk 3

T m ^—     Z .

Теплофизические свойства воздуха при температуре Т_m :

λ в m = λ в (T m ); μ вm = μ ж (T m ); c вm = c ж (T m ) . (24)

Тогда:

Num = C, Rammт,(25)

где коэффициенты C₁ , n₁ определяются из следующей таблицы:

Таблица 2. Значения коэффициентов

Ra m	C l	n l
10-3÷5·10-2	1,18	0,125
5·10-2÷2·107	0,54	0,250
2·107÷1013	0,135	0,333

Ram = GrmPrm,(26)

где Ra_m – число Рэлея; Gr_m – число Грасгофа:

IN

Grm = gd^Tm (Гз,2 - Te )Pm -(

Me g – ускорение свободного падения, м/с2, β= Tm-1 – коэффициент объёмного расширения воздуха;

M ^em c ^em

^Pr m - ₀     .                (28)

^A em

Шероховатость получаемой поверхности может быть оценена по формуле, предложенной [7]:

R Z - - 2,1 + 0,098 v - 0,005 s + 0,029 Z + 0,0011 vs . (29)

Таким образом, охлаждающая технологическая среда и способ её подачи влияют на тепловую напряжённость процесса разрезания полимерных композиционных материалов отрезными алмазными кругами. Это видно через изменение следующих показателей:

• 1)    поверхностной плотности теплового потока, отводимого из зоны контакта за счёт нагрева и парообразования СОЖ (см. [2] зависимость (1));

• 2)    коэффициентов теплоотдачи на участках свободных поверхностей режущей кромки и корпуса отрезного алмазного круга и заготовки, контактирующих с С ОЖ (с м. [ 2] – и за висимости, определяющие a _pk , a _k , a ₃ , а _пл ).

Ранее были разработаны математические модели см. [2], задач теплообмена при разрезании заготовок из полимерных композиционных материалов алмазными отрезными кругами. В моделях показана связь теплового состояния контактирующих объектов с характеристиками охлаждающих технологических сред, характеристиками их подачи в зону обработки, с реальной формой взаимодействующих объектов и зоны контакта. Это поможет найти оптимальные условия подачи СОТС при разрезании для минимизации температурных напряжений, то есть, в итоге, улучшить качество получаемых деталей.