Влияние соотношения геометрических размеров на гидродинамическое сопротивление при течении неньютоновской среды в призматических каналах при условии равенства периметров поперечного сечения

При решении задачи теплопереноса при небольших разницах температуры уравнения переноса количества движения и неразрывности можно решать независимо от уравнения теплопроводности при условии, что теплофизические характеристики процесса меняются незначительно. Кроме того, очевидно, что гидродинамическая структура потока оказывает сильное влияние на характер процесса теплообмена, и в большинстве случаев получение решения гидродинамической задачи, а именно в случае неньютоновских сред, представляет наибольшую трудность, поэтому данная работа посвящена решению этой проблемы. Одной из основных характеристик теплообмена является площадь поверхности теплообмена, вследствие чего, решение гидродинамической задачи наиболее целесообразно проводить при равных площадях поверхности теплообмена.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Математическая модель ламинарного течения неньютоновской жидкости в призматическом канале (рис. 1) построена при следующих допущениях:

1) течение жидкости изотермическое, стационарное, ламинарное, со сформировавшимся профилем скорости на входе в канал; 2) жидкость несжимаема; 3) физические свойства жид-

кости постоянны; 4) массовые силы пренебрежимо малы; 5) реологическое поведение среды, характеризуется наличием нелинейно-вязких свойств.

дP дz

. ■ 1дx \ дx J

1 <>(и

В качестве граничных условий приняты условия прилипания жидкости на стенках канала y=0, y=h: v = 0 ,            (2)

x=0, x=b: v = 0 .            (3)

На входе в канал задается ньютоновский профиль скорости.

Для описания реологических свойств 0,65% раствора Na карбоксиметилцеллюлозы (КМЦ) использовалась модель дифференциального типа [1]. В качестве конкретной зависимости взята модель Кутателадзе-Хабахпашевой [2, 3]. Экспериментальные данные при течении 0.65% раствора Na-КМЦ в круглой трубе [5]. Для диапазона I ₂ <500 согласно [2, 3] построена регрессионная модель вязкости при T₀ = 293 (К),

Рис. 1. Призматический канал прямоугольного сечения

р.( 1 2 ) = 0,0756312 - 9,03685*10 ^{- 6} 1 ₂ + 0.492196(1.0561 + 0.019904 1 2 ) -

50 + 1 ₂

- 0.000339989*293 + 2.38648*10 ^{- 8} *293 1 ₂ +

+ 4.02062* 10 — 7 293 2 - 3.26264* 10 ^{- 10} 1 22

Погрешность между регрессионной формулой и аналитической моделью Кутателдазе-Ха-бахпашевой составляет менее 0,5%. Исходное уравнение (1) с граничными условиями (2)-(3) решалось методом конечных элементов.

РЕЗУЛЬТАТЫ РАСЧЕТОВ

Расчеты проводились при р =1014 (кг/м3), С p =3591 (Дж/(кг*К)), Х = 0,5618 (Вт/ (м*К)). В работе размеры сечения призматического канала выбирались из условия равенства периметров p=0,2392 (м):

а) (h=0,0598; b=0,0598 соответствует b/h=1), б) (h=0,0398; b=0,0798 соответствует b/h=2),

в) (h=0,0299; b=0,0897 соответствует b/h=3), г) (h=0,0199; b=0,0997 соответствует b/h=5).

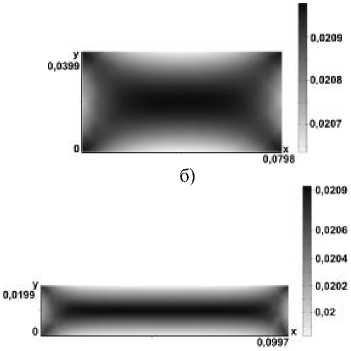
В ходе выполнения численных расчетов получены следующие распределения I 2 и Ц по сечению канала на промежуточной границе (рис. 2, 3). Как видно из рис. 2, для жидкости 0,65% раствора Na-КМЦ в пристеночной области наблюдается максимальное увеличение второго инварианта тензора скоростей деформации, поэтому жидкость у границ канала менее вязкая. Данное явление является характерной чертой для всех псевдо-пластичных жидкостей [1].

Влияние геометрии канала, в данном случае соотношения b/h, связано с тем, что c увеличением b/h увеличивается значение I₂, а именно b/ h=1 (I 2 ) max =19 (1/с²), b/h=5 (I 2 ) max =275 (1/с²). При этом значение вязкости, наоборот, уменьшается с ц mjn = 0,0207 (Па*сек) для: b/h=1 до ц min = 0,0199 (Па*сек)дляb/h=5.

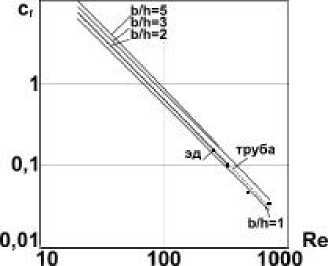
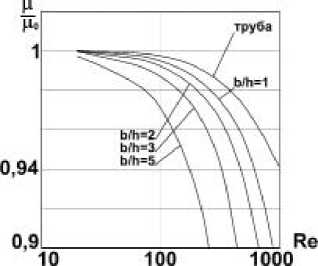
На рис. 4 представлены зависимости коэффициента сопротивлению трению C_f и отношения Ц / Ц 0 ( Ц д вязкость при Т=293(к) I 2 =0(1/ с²)) от числа Рейнольдса для ламинарного течения 0,65% раствора Na-КМЦ [5].

а)                                                         б)

в)                                                        г)

Рис. 2. Распределение второго инварианта тензора скоростей деформации (I₂) по сечению канала, Re=80

в)

Рис. 3. Распределение вязкости по сечению канала, Re=80

г)

• ^а)                                               б)

Рис. 4. а) зависимость коэффициента сопротивления трению от числа Рейнольдса для ламинарного течения 0,65% раствора Na-КМЦ, эд – экспериментальные данные по круглой трубе, L=1; б) зависимость отношения текущей вязкости к начальной ц q = ц (0,293 ) в (6)

С f =

D_э ^P /4 L

Р u ^ /² ’

D э – эквивалентный диаметр канала, Δ P – разность давления в исследуемом участке, ρ – плотность жидкости, u m – средняя скорость течения.

ВЫВОДЫ

В ходе исследования ламинарного течения 0.65% раствора Na-КМЦ в призматических каналах одинакового периметра было получено, что коэффициент сопротивления трению увеличивается с увеличением отношения ширины канала к высоте, при этом вязкость наоборот уменьшается. Максимальное среднеквадратичное отклонение между численными результатами в круглой трубе и экспериментальными данными (эд) составляет менее 10 %.

Работа выполнена при финансовой поддержке ФЦП “Научные и научно-педагогические кадры инновационной России” на 2009 - 2013 годы”, государственный контракт № П1212