Влияние сопротивления лицевого слоя солнечного элемента на выходные характеристики устройства

Ведение. Солнечные элементы широко используются в космических аппаратах [1-12]. Одной из важнейших задач технологии солнечных элементов (СЭ) с лицевым n ⁺-слоем является уменьшение омических потерь этого слоя на фоне других факторов, ухудшающих рабочие параметры СЭ.

Обычное выражение для ВАХ СЭ [11-14]:

	I C =- I pn + I v ,	(1)
где	Г q ( V + I c R ) >
где	I pn = 1 0 e 0 - 1 V             7	,                   (2)
	0 = кТ ; R = p 1 1 ; w1 2	(3)

R - сопротивление лицевого слоя; р - его удельное сопротивление; w - толщина; 1 1 - длина (от середины n ⁺-слоя до собирающего электрода); 1 ₂ -протяженность собирающего электрода; I _v - фототок СЭ при R = 0; I_pn - обратный ток из n ⁺-канала в p -область; I ₀ - обратный темновой ток p-n -перехода.

Уравнения (1), (2) отражают модель, в которой сопротивление лицевого слоя учтено как последовательно соединенное с p-n ⁺-переходом сопротивление.

Минимизация сопротивления n ⁺-канала должна осуществляется самосогласованно с конструкцией СЭ, обеспечивать максимальную прозрачность лицевого слоя для проникновения в p -область света, а главное, не ухудшать это качество при длительной эксплуатации СЭ, например, в условиях радиационного воздействия в космосе.

В связи с этим интересно рассмотреть более точные модели учета влияния омических потерь n ⁺-канала на вольт-амперные характеристики СЭ.

Влияние сопротивления n ⁺-канала на вольт-амперные характеристики СЭ. В [13-15] показано, что для расчета вольт-амперных характеристик СЭ с n ⁺-каналом, необходимо использовать уравнения рассредоточенных токов j ( x ) и потенциалов ф ( x ) в канале. Учитывая, что возрастание тока а / ' на пути А х в канале обусловлено притоком электронов из p -области - I ф 1 ₂ А x , запишем:

j = 121ф, (4) dx где 12 - протяженность собирающего электрода,

Iф = - Ipn + Iv; (5)

qφ rpn = Iо e 0 -1 .

Аналогичным образом для падения напряжения в n-канале запишем dФ = - R/(7)

dx1

Из (7) получим:

1 ^{1 1}

Аф = (-V + фо ) = R- J j(x) dx.

' 1 о

Решение уравнений (4)-(7) будем рассматривать с учетом граничных условий:

j = 0, ф = ф ₀ при x = 0

j = I , ф = V при x = 1 1

где ф ₀ - потенциал середины n ⁺-слоя.

Влияние сопротивления лицевого слоя на параметры СЭ можно проанализировать с помощью компьютерного интегрирования уравнений (5)-(7). Для этого преобразуем их по методу конечных разностей, превратив их в следующие рекуррентные отношения:

Jk + 1 = Jk + 1 ф (Ф к ) А к ,               (10)

Ф к + 1 = Ф к — R/ k А к ,                (11)

где

Г q-.

I ф (Ф к ) = I v - 1 0 e ⁰ - 1

Систему рекуррентных соотношений (10)-(12) будем решать при граничных условиях:

jk = 0, ф к = ф 0 при к = 0 ( x = 0)

. (13) j N = I , Ф N = V при к = N ( x = 1 1 )

Здесь N А к =1, 1 1 = N A x , N - число разбиений участка 1 1 на элементы A x . При этом (как и выше) здесь и ниже токи I_v , I ₀, I ф , j_k и сопротивление R будем относить к единице освещенной поверхности СЭ так, что 1 1 1 2 = 1.

При этом ф₀ (потенциал середины n ⁺-слоя) так же, как и все j_k и ф _к , независимы, а I_v , I ₀, R и 1 1 являются параметрами модели, от которых следует изучить зависимость ВАХ СЭ.

С учетом нелинейности уравнения (12) решение уравнений (10), (11) требует нестандартного подхода. В нашем случае задача существенно упрощается, если ф₀ рассматривать как аргумент, от которого выходные ток jN = I и напряжение ф₀ = V зависят параметрически.

Из физических соображений следует, что ф0 лежит в интервале фкз < ф0 < Vxx. Каждому ф0 в этом интервале однозначно соответствует своя пара значений фN = V и jN = I, совокупность которых и образует ВАХ СЭ. При этом фкз определяется как то значение ф0, при котором V = 0 и I = Iкз.

На рис. 1 показана серия ВАХ, рассчитанных для типичных СЭ с параметрами I_v = 25 мА/см² и V_xx = 0,6 В и различающимися сопротивлениями лицевого слоя R (на рис. 1 приведены кривые для различных 1 1 , так как R ~ 1 1 ).

Для анализа результатов рассмотрим уравнения (4)-(7) интегрированием их отношения:

JdJ = - ¹ 1 Ф ⁽Ф) d Ф.                ⁽¹⁴⁾

R

Здесь и ниже положено 1 1 1 ₂ = 1, и поэтому I ф , I _v , I , а также R будут рассматриваться на единицу освещаемой поверхности СЭ.

Учитывая (5), интегрирование (14) дает

2, j =х[Ф(Фо) — Ф(Ф)], R

На рис. 1 видно, что при R <  R_n ~ 4 Ом/см² вольт-амперная характеристика СЭ приближается к идеальной, у которой I _кз не зависит от R . В то же время при R > R_n эти параметры уменьшаются обратно пропорционально RR в полном соответствии с (19) и (20).

Необходимо отметить, что при больших расстояниях между электродами в середине межэлектродного пространства даже при токе короткого замыкания должна существовать «нейтральная» зона, в которой фототоки сбалансированы обратными токами из n ⁺-канала в базовую p -область. Протяженность этой части канала будет определяться из условия j ( x = 1 1 -- X) = y I , где y << 1 — величина, задающая требуемую точность расчетов (~0,01), X - протяженность активного участка канала, прилегающего к электродам, в котором собирается основная часть фототока.

Если на этом (11 - X < x < 11) участке n+-канала пренебречь обратными токами, то возрастание тока в n+-канале в X-области будет происходить по линейному закону, и тогда, как не трудно показать с помощью (8), где

Ф (ф) = ( I v + I о )ф-- ^q

^

e ®

- 1 1 0 .

Здесь ф ₀ (как и выше) - потенциал середины ( x = 0) n ⁺-слоя. Это уравнение справедливо и для x = 1 1 , где j = I и ф = V . При этом для ВАХ СЭ получается следующее уравнение:

1 ² = - [Ф (Ф 0 ) -Ф ( V ) ] ,

R

I ² = - Аф

R

qV

I v + I 0 - I 0 e ® F (а)

где q . eа -1

Аф = фо - V , а = —Аф, F (а) =-----.        (17)

0           а

В этих уравнениях фигурирует параметр ф ₀, для определения которого можно использовать уравнение (7) в интегральной форме:

7 d Ф

R = ----.

V j ⁽Ф)

Из (15) и (16) устанавливается следующая связь между ф кз и I _К з :

I _к ² ₃ = 2- Ф (ф_кз).                   (19)

R

При больших R R —— максимальное значение I      I кз )

I 2 достигается при ф ~ V_xx и согласно (19) зависит от R по закону

I КЗ = — Ф(ф_к з). кз кз

I        V» I

В то же время при малых R I R <<  — I величина

I       I кз )

ф_кз « — RI_K3 кз ₂ кз

и поэтому I _кз ~ I_v , т. е. слабо зависит от R .

А ф = ^X1 RI . (21) ' 1 ²

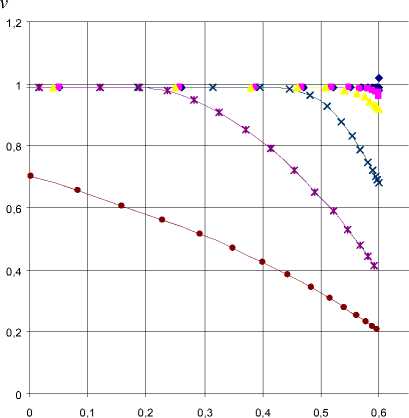
Здесь величина v = X/ 1 1 представляет собой долю активной части лицевого слоя СЭ. Она зависит не только от 1 1 (точнее - от R ), но и от выходных тока и напряжения СЭ. Пользуясь численными методами, изложенными выше, мы рассчитали Аф и v = Аф/^ ZR в зависимости от I и V серии СЭ с разными R . Результаты расчетов представлены на рис. 2.

Из этих расчетов видим, что в хорошем приближении ВАХ СЭ приближается к идеальной ( v ~ 1) при R <  R n , где R n = 4 Ом/см². В то же время при R > R_n область идеальности уменьшается в сторону меньших выходных напряжений ( V <  V_n , где V_n = 0,45 В для R = 6 Ом/см² и V_n = 0,22 В для R = 25 Ом/см²) и, следовательно, больших токов. Параметр неидеальности v связан с коэффициентом заполнения ВАХ СЭ n = I m V m / 1 кз V™ , где I m V m -максимальная мощность выходного тока при заданных I_v и V_xx . Расчет показывает, что V m ~ V_n , так что определение V_n и, соответственно, I m очень важно для оптимизации электрических режимов эксплуатации СЭ.

Заключение . Таким образом, с учетом распределения потенциалов и токов в лицевом n ⁺-слое солнечных элементов n ⁺- p -типа получено выражение для их вольт-амперных характеристик в зависимости от параметров лицевого слоя. Проведенный анализ уравнений (4)-(8) позволил представить уравнение ВАХ СЭ в новой форме, более точно описывающей зависимость выходных параметров СЭ от R , а также от характеристик p - n -перехода. Показано, что при сопротивлении лицевого слоя R >  R_n (~4 Ом/см²) ток короткого замыкания ( I _кз) и коэффициент заполнения ( п ) уменьшаются обратно пропорционально RR , а при R <  R_n ВАХ практически не зависит от R . Сопротивление лицевого слоя солнечного элемента влияет на вольт-амперные характеристики. В условиях космоса деградация параметров СЭ происходит в значительной степени из-за возрастания сопротивления лицевого n ⁺-слоя, пересыщенного донорами в условиях облучения.

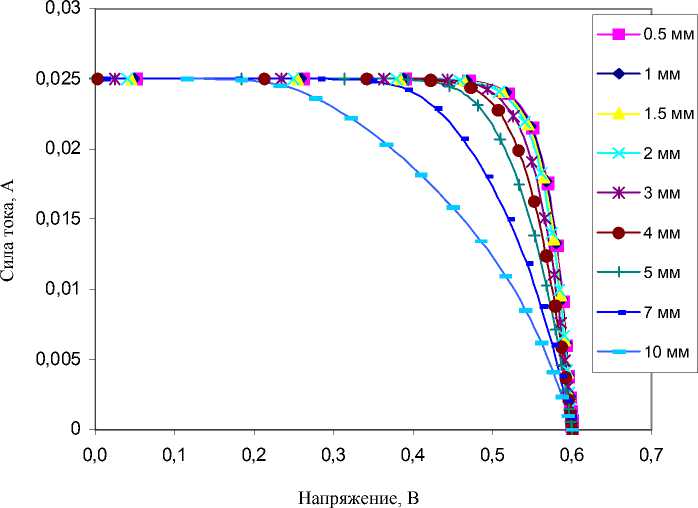
Рис. 1. Расчетные ВАХ для СЭ с I ф = 25 мА/см² и V_хх = 0,6 В

Напряжение, В            а

—♦— 0,00625

0,25

6,25

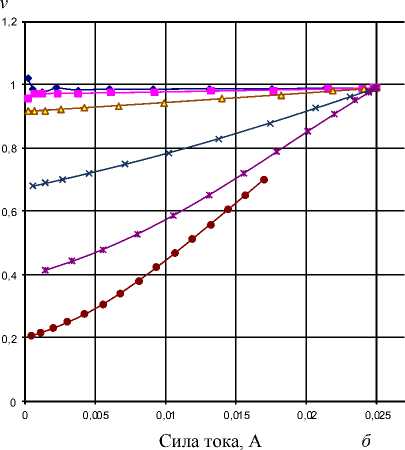
Рис. 2. Зависимость ν от V ( а ) и I ( б ) для разных значений R ( l ₁)