Влияние сотового наполнителя на размерную стабильность трехслойных параболических углепластиковых рефлекторов

К параболическим рефлекторам, используемым в качестве элементов антенн на космических аппаратах, предъявляются высокие требования по размерной стабильности в процессе эксплуатации. При неравномерном нагреве солнцем и охлаждении в тени среднеквадратичное отклонение <СКО) поверхности рефлектора от идеальной параболической формы не должно превышать заданной величины. Конструктивно рефлектор состоит из двух многослойных обшивок из волокнистого углепластика, скрепленных сотовым наполнителем (СН). При анализе рефлектор полагается тонкой термоупругой трехслойной ортотропной оболочкой типа Кирхгофа - Лява. Постановки соответствующих задач объемной нестационарной теплопроводности и термоупругости приведены в [1]. Обычно при расчетах таких конструкций на силовое нагружение жесткостью СН пренебрегают ввиду ее малости. В случае же -температурного нагружения влияние наполнителя для размеростабильных конструкций может быть существенным из-за большего, чем у силовых обшивок, коэффициента линейного температурного расширения (КЛТР).

Влияние температурного расширения СН определим из решения следующей задачи. Трехслойный пакет, занимающий область О (рис.)) с границей S , находится при температуре Т . Полагаем, о что температура в области О изменяется на величину е. Считая границу S свободной от нагрузок, найдем изменение линейных размеров пакета в направлении координатных осей х> у. Полагаем материал обшивок ортотропным, СН - изотропным. Главные направления тензора свойств материала обшивок и направления выкладки СН совпадают с координатными осями х, у- При деформировании стенки сот не теряют устойчивость. В области П выполняется гипотеза плоских сечений. В обшивках реализуется плосконапряженное состояние ^.^ 0^> в стенках сот - одноосное. Тензор упругих деформаций е есть разность полных е и температурных деформаций ёТ:

с = е - е .                                                    (1 )

С учетом принятых предположений определяющие соотношения для материала обшивок имеют вид [2]"-

Рис. 1. Схема 'трехслойного пакета.

1,2 - силовые обшивки толщиной н, 3 - сотовый наполнитель толщиной И-

- (и) К ( е (и) - е^Т + р 1 е Си) - е* )), (х^у), (2)

X                     х            >:       х       у            у где еТ :     е. Е = Е / ( 1 - р Р )), и         .         х х                   х у

• е. ( и ) - ® и / д $-, pxwy)', вектор перемещении;

<л «х >. у <£ > - КЛТР, модуль Юнга по оси х<уХ X у X у

• > - коэффициент Пуассона, характеризующий сокращение в направлении оси у<х> при растяжении в направлении оси

Из симметрии упругих свойств справедливо соотношение :

Р К = р Е

X X       у '

Из гипотезы плоских сечении и симметрии напряженно- деформированного состояния <НДО следует, что сдвиговые деформации £ху и соответствующие им напряжения равны нулю.

Для материала <Н <рис. 2> :

= Ес

а в )

Вариационная постановка краевой задачи для области О без

3 5(й)  • e(v) <Ю = О, V и е П_доп

где U - кинематически допустимое множество доп е - тензор деформаций.

перемещений,

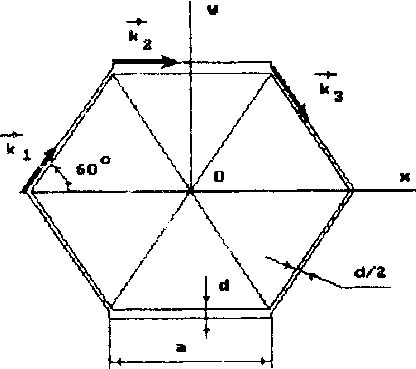
Рис. 2. Ячейка сотового наполнителя.

а ~ размер ячейки, d - толщина ленты.

Для нахождения двух искомых эффективных КЛТР пакета <а >, <а >, X        у соответствующих случаю однородного температурного поля, выберем последовательно две пробные Функции v , v е U , которые, пос1   2 ДОП ле подстановки их в <4>, дадут два линейно независимых уравнения относительно искомых величин. В качестве первой пробной Функции выбираем такую, чтобы S^v) = 44, второй - чтобы s^v) = jj> где i, J - единичные орты для осей ж, у, 4 4, jj - диадные произведения векторов. Из гипотезы плоских сечений следует соотношение между полной деформацией стенки соты е и полными деформациями обшивок е :

e = k e k = k (eti + ejj) k,        (5)

где к ~ единичный вектор, характеризующий положение стенки соты (векторы к , к , к указаны на рис. 2>.

12 3

После подстановки пробных Функций v^ и и^ в С4> с учетом <2>, <3>, <5> и необходимых преобразований приходим к системе двух уравнений относительно компонент полных деформаций пакета

4  е + 4 е = 6 В ,

Их   12 у1

4  е + А  е = 6 В ,

12 х      22 у2

где 4  = а + с , 4    = а + с ;

И 11 И 22     2222

А - р а + 3 с / 17; 12х

В = а (а + а р ) + 20 с а / 17; 1      11 X у X11 с

В = а. (о*ар)*4о а / 3;(7)

2      2 2 У     х у22 с а = 8 Ё h ( 373 а + 2d ). а _ = 8 Е h ( зУз а + 2d ); 11         X22

с = 17 Е И d> с = 9 Е Н d. 41           с          22с

Решение системы (б) имеет вид :

е = в С В А -В А 1 /

X        1 1 22     2 12 > '

еу = ® < Вг Ai - В1 Аг Z А> где Д = А^ А^ А^.

Эффективные КЛТР пакета <ох>, <ау> определяются из соотношений :

<а ) - е / в, <а > = е / в.(9)

XX    уу

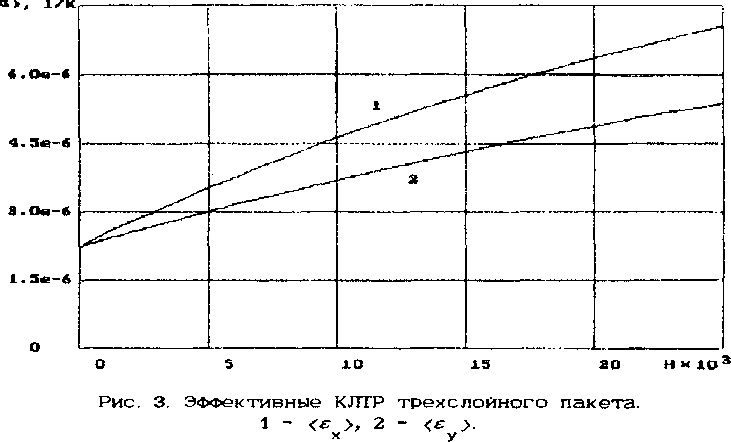
Эти величины количественно характеризуют влияние СН при однородном нагреве. При нулевой толщине обшивок < Н = О > эффективные КЛТР пакета <а >, <а как и следовало ожидать, равны КЛТР х у материала СН а^. На рис. 3 приведена зависимость <ш >, <а > от толщины СН И для пакета с четырехслойными обшивками из углепластика КМУ-4Л с выкладкой 0-90-90-0 и толщиной h =  6" 10 * м.

Эффективные характеристики обшивок Е - Е = 72.64 ГПа, р - р = 0.01743, «х - ®  - 2.23" 10 6 1/К. В качестве наполнителя ис пользованы алюминиевые соты с параметрами а = 3- 10 3 м, d 5' IO"5 м, Ег - 108.25 ГПа, а^ - 1 .67' 10~S 1/К. Каи видно из приведенных графиков, действительно, за счет больших КЛТР наполнителя эффективный КЛТР пакета может в 2..3 раза превышать КЛТР-обшивок.

Для практических расчетов в случае неоднородных температурных полей найдем эффективные механические характеристики СН. Симметрия выкладки его относительно осей х. у позволяет записать определяющие соотношения в виде, совпадающем с <2>:

<сгх(и)>

<Ех> ( ех(и)

ех + <их> ( еу(и)

ej )    (х*»У ) - (10)

При изменении температуры в области О на величину в в любых сечениях, параллельных плоскостям Oacz, Oyz , выполняются уравнения равновесия:

J о (и) ds = J о fu) ds = О, зхS из которых с учетом соотношений <2>, <101 получаем уравнения :

<Е > ( е -а 6 * <р > ( е - « в )) К * X   X   С     хус

Е ( е - « 6 + Р ( е - а в )) 2 h = О, (х**у),(11)

XXX  X уу где полные деформации ех, еу определены соотношениями <81. Недостающие два уравнения для нахождения четырех неизвестных <Е >, <Е >, <Р >, <Р > получим, рассмотрев НДС области О при изменении температуры на величину е последовательно при двух условиях : сначала потребовав е х(и) = О, затем е Си) = О Для первого случая пробную Функцию выбираем такую, чтобы e(v) =ii, для второго - чтобы e(t>2)  = jj- После подстановки пробных функций у и v в <4) с учетом определяющих соотношений <21, 12

• < 10> и необходимых преобразований получаем систему четырех уравнений :

<Вх> ( а^ * а12 <Рх> ) =c

<Ёу> ( «21 + ам <Ру> ) =с

<Ё_х> ( а_{м + %2} <р_х> ) ^ с_з;

) - %> где а = С В / А - а ) И, а - а Н;

11      _ 1      11 с         1Zс с = - Е (В / А ( а * р а )) 2 Н; 1          X      1      11          XX у

»2i = СД Х 4г - « > Н, ^2 = - о. Н;

с₂ = - Е_у t В₂ / А^ - б «_у 4 Р_у а_х )) 2 К,

Д₃₁ - б <« >       ) И, t^₂ = ( <а >  - а_с) И;

с = - В ( <а > - а 4 р f <а > - а )) 2 h; 3        X       X       X      X       уу а = б <« > - а ) Н, а о = f <а > - а ) Н;

41      _ У       с          4 2         Xс с = - В б <« > - а 4 р ( <а > - а )) 2 h;

4        у      у      у у      XX

<а >, <а > определяются соотношениями (9); х У

А , А , В , В - соотношениями (7). 11    22    12

Решения сис-гемы уравнений (12) имеет вид:

<Е_х> = б с^ _а2 - е_за ₁₂ ) / б а₄₁ а_д2 - а_{12% ±}

• _{< Рх}> = ( ^ / <В_х> - а _t ) / а₁₂ ;

• < V = б с₂ / <Е_у> - «₂₁ ) / а₂₂;

Эффективные модули Юнга СН определяются из соотношений:

• < Е > - <В > ( 1 - <р > <р > ),   (х*»у).(14)

XX     X  у"

Искомые величины, определенные выражениями (13), не должны зависеть от характеристик материала обшивок В> В , р , р , а , X у X у X а , толщин h, и Н, КЛТР материала СН а . Следовательно, соотноше-у                                             с ния (13) могут быть упрощены, однако непосредственные их преобразования требуют громоздких вычислений. Для упрощения соотношений (13) проанализируем структуру коэффициентов А^, А 1г> В^ В2 (7). Коэффициент А есть сумма двух слагаемых : а и с , при-11                                              11         11

чем коэффициент а.^ характеризует вклад от обшивок, коэффициент с - от СН. Примем во внимание, что вид определяющих соотноше- 11

ний для СН (10) совпадает с видом определяющих соотношений для обшивок (2). В этом случае коэффициент с^ для СН есть аналог коэффициента а для обшивок. Рассуждая аналогично, можно заклю- чить, что в выражении для коэффициента В второе слагаемое есть 1

аналог первого. С учетом изотропии КЛТР материала СН эти аналогии позволяют записать :

с ( 1 4 <р > ) а = 20 с а /17, 11               X        с           11 с откуда находим, что <р> = 3/17. Преобразовав выражение для коэффициента а , получим :

Ех= а^/ ( 2 h 4 ( 3 V3 а. + 2 d )).

Использование отмеченной аналогии между коэффициентами ^ и а^ позволяет записать :

<Ех> = с^ / ( Н 4 ( 3 73 а + 2 d )) =

= 17 Ес d / ( 4 ( 3 73 а + 2 d ))•

Рассуждая аналогично, из анализа коэффициентов Дга, вг находим, что <р > = 1/3, <Е > = 9 Е d / ( 4 ( 3 73 а. + 2 d ) )■ С учетом у               Xс соотношений (14 ) окончательные выражения для эффективных упругих свойств СН имеют вид :

• < Е_х> = 4 Е^ d / ( 3 73 а + 2 d )">

• < Е > = 36 Е d / ( 17 ( 3 73 а + 2 d ))",(15)

Ус

• < Р > = 3/17,       <ц > = 1/3-

• XУ

Чтобы убедиться, что (15) действительно есть решение системы ( ;2), достаточно подставить (15) в (12), что приводит к тождествам.

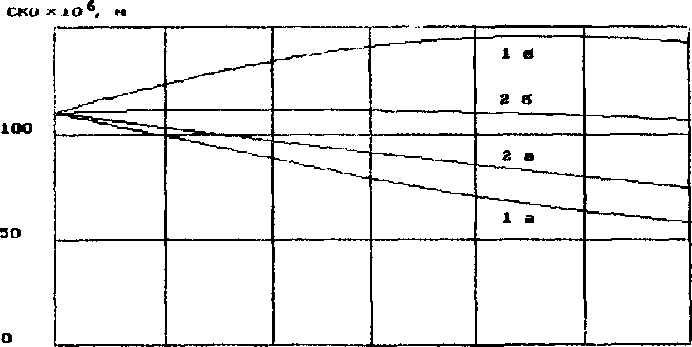
5        1О      15       20       25 НхЮ3, м

Рис. 4. Влияние термического расширения сотового наполнителя на размерную стабильность рефлектора.

а - без учета, б - с учетом расширения наполнителя.

Алюминиевые соты d=5xlO~^SM, 1 - а=Зх10^Эм, 2 - а= 1,2х 1 0 ²м.

Для рассмотренного ранее примера эффективные модули Юнга СН составляют: <Е > = 1.4 ГПа, <Е > = 0.7 ГПа, что на два порядка х                     У меньше модуля упругости обшивок. Существенное влияние на поведение конструкции наполнитель со столь низкими жесткостными характеристиками обеспечивает , во-первых, за счет больших, чем у обшивок, КЛТР, и, во-вторых, за счет значительно большей толщины по отношению к толщине обшивок. В реальных СН толщина ленты d много меньше размера ячейки а, Анализ соотношений (15) с учетом приведенного замечания позволяет заключить, что эффективные модули Юнга СН <Е >, <Б > практически линейно возрастают с ' и у' увеличением толщины ленты d и быстро убывают с увеличением размера ячейки о-

ЭФФективные механические характеристики наполнителя позволяют при расчетах реальных конструкций рассматривать его как однородный ортотропный материал с КЛТР, равным КЛТР материала СН. Такой подход был использован при оценке размерной стабильности параболических рефлекторов. На рис. 4 приведены результаты расчетов для рефлектора диаметром 0.9 м с характеристиками, указанными ранее в примерах. Рассмотрен случай наиболее неблагоприятного, даюшего наибольшее СКО, нагрева рефлектора солнцем под углом 75° к оси рефлектора. Как следует из приведенных графиков, расчеты без учета влияния наполнителя приводит к существенным погрешностям . Эти погрешности возрастают с увеличением толщины сот и их ’Чессивности" (увеличением d, уменьшением а>.

Еывшш

Уточненные расчеты Формоизменения трехслойных размеростабильных оболочечных конструкций при температурном нагружении требуют учета температурного расширения сотового наполнителя. Необходимые для этого эффективные характеристики наполнителя могут быть найдены по предложенной в данной работе методике и расчетным Формулам.