Влияние спектра полупроводникового лазера на ФРТ дифракционного микрообъектива для лазерной считывающей головки

ВЛИЯНИЕ СПЕКТРА ПОЛУПРОВОДНИКОВОГО ЛАЗЕРА НА ФРТ ДИФРАКЦИОННОГО МИКРООБЪЕКТИВА ДЛЯ ЛАЗЕРНОЙ СЧИТЫВАЮЩЕЙ ГОЛОВКИ

В [']• Г2] сообщалось о результатах работы по созданию дифракционного микрообъектива (ДМО) для считывающей головки лазерного цифрового проигрывателя. ДНО был рассчитан и изготовлен для работы с полупроводниковым (п/п) лазером в оптической схеме с переносом изображения "из точки в точку". При расчете предполагалось, что источник света точечный, одночастотный. Однако в зависимости от условий работы, температуры кристалла, срока службы и т.д. число продольных мод и длина волны основной моды в излучении п/п лазера могут изменяться, что приводит к появлению сферических аберраций. Цель работы - определить (теоретически и экспериментально) допустимые отклонения в спектре излучения источника света, которые не влияют существенно на качество изображения ДМО.

Качество фокусирующих объективов для считывающих головок удобно оценивать по критерию Марешаля [3], который связывает нормированную интенсивность в дифракционном фокусе (число Штреля Q) со среднеквадратичным отклонением фазы волнового фронта от опорной сферы (ДФ)2. Если аберрации малы, то

Q Z 1 - (ДФ)2,                                                                          (1)

где

Q = 1/10 - отношение максимальных интенсивностей в аберрированном дифракционном изображении точечного источника I и в изображении, сформированном той же системой при отсутствии аберраций 10;

(ДФ)2 = Ф2 - (Ф)2 - среднеквадратичная ошибка Фазовой функции ДМО.

Фазовая функция ДМО вычислялась для определенных параметров: длины волны X; апертуры а; толщин d1 , da подложки и защитного стекла с показателем преломления П1 и па' Расстояния источника и изображения до дифракционной структуры без учета знаков z1, z= (рис. 1). Для изготовления фотошаблонов использовались члены разложения функции по р до восьмой степени (р - расстояние от центра структуры ДМО, изменяющееся от 0 до а). Для определения технологических допусков достаточно ограничиться четвертой степенью разложения

Ф = (а, + аа)р2 - (В, + В3)р“,                                                 (2)

где

• а, = 2п/(Х • Ь,л); а3 = 2п/(Х • Ь31);В1 = <2п/Х)(Ьлз/Ьлл); В3 = (2п/Х) (Ь33/Ь^);

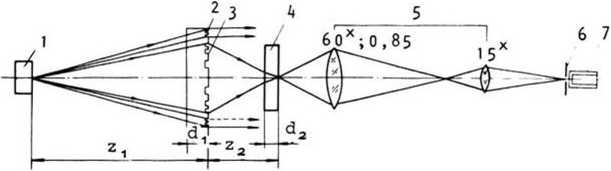
Рис. 1. Оптическая схема установки для исследования ФРТ дифракционных микролинз: 1 - источник излучения; 2 - дифракционная микролинза; 3 * вспомогательная кольцевая микролинза для настройки схемы; ^ - пластинка, имитирующая защитное покрытие компакт-диска;

5 - микроскоп; 6 - микродиафрагма;

7 - фотоумножитель b11 = 2[z, + d, {(1/n,) - 1}]; b21 = 2 [z2 + d3{(1/na) - 1}];

Ь31 = 2[z, + d^d/n’)- 1)]; b23 = 2[z3 + d,{(1/n= ]- 1}].

Найдем ошибку фазовой функции д<р при изменении длины волны X; для этого учтем, что во всех коэффициентах (2) зависимость от X проявляется в виде умножения на (1/А) , например, За/ЗХ = -а/Х,

Ф = ДФ = ( - у1 ДХ - ^ ДХ + д2 )Р2 + (|1 ДА + Ь. дЛ - ^ Дг3)р“, (3) где Хо _ расчетная длина волны.

После вычисления среднеквадратичной ошибки по (1) находим число Штреля Q при подходящем выборе центра опорной сферы Дг

“. - £<а, *«_aw^;

= - i-|^ te, ♦ 6, - ^ («, * q,)^ Г ^ ■                   «)

Расчетное значение ДХ при Q > 0,8 составляет 132 X.

Оценка влияния ширины спектра источника на качество изображения проводилась по следующей аналитической формуле [3]:

° ■ А °" '^р7^,= '                                  151

где

(2к+1) - количество продольных мод; сп - вес n-й моды;

n = -_2Tta2 д ^  _ длина ВОЛны основной моды, Д - расстояние между сосед-

Ч z2 0 ними модами).

Практическая оценка системы по значению Q не всегда возможна, так как неиз вестно реальное абсолютное значение Q для идеальной системы. В таких случаях качество изображения можно контролировать по функции рассеяния точки ФРТ [3], например, по отношению интенсивности в 1-ом максимуме и минимуме к максимуму интенсивности в центре. В безаберрационном изображении интенсивность в 1-ом максимуме составляет 1,75%, а в минимуме равна нулю.

Экспериментальная проверка качества изображения ДМО проводилась на установке оптическая схема которой приведена на рис. 1. Распределение интенсивности в фокальной плоскости ДМО переносилось с увеличением -1000 на подвижную цель с фотоумножителем и фиксировалось на ленте самописца. В качестве источников излучения использовались He-Ne лазер (X = 0,63 мкм), который, можно считать, не вносит аберраций в ФРТ микролинзы и полупроводниковый лазер типа ИЛПН-210А (X = 0,79 мкм), ширина спектра которого задавалась режимом работы. Изменение ширины спектра п/п лазера достигалось путем регулирования температуры кристалла ступенчато через ~2°С при постоянном токе накачки. Одновременно это приводило к изменению мощности и сдвигу длины волны. Экспериментальная зависимость мощности излучения от температуры кристалла представлена на рис. 2, мощность дана в значениях тока диода J, помещенного за лазером. Сдвиг длины волны излучения для всех используемых режимов работы лазера относительно расчетного значения не превышает 17 А (рис. 3), что лежит в допустимых пределах (132 А), и его влияние на ФРТ можно не учитывать.

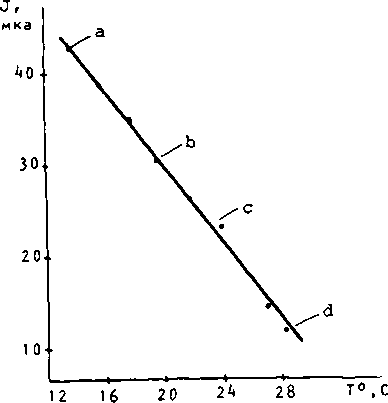
Рис. 2. Зависимость тока диода J от температуры кристалла Т

Спектр излучения п/п лазера при всех режимах записывался на спектрометре ДФС-21!. На рис. *» графически показано, как изменяется ширина спектра источника в соответствии с различными значениями тока диода. Согласно рисункам 2 и ^ наиболее узкий спектр шириной от 1 до 10 А (1-3 продольные моды) наблюдается при температуре кристалла от 1^ до 20°С. Ширина спектра определялась на уровне 0,1 интенсивности основной моды. Наиболее характерные спектры излучения п/п лазера приведены на рис. 3. Они соответстеуют точкам a, b, С и d на рис. 4. Распределение интенсивности в фокальной плоскости ДМО, записанное с лазером, работающим в указанных режимах, представлено на рис. 5 (a-d), а на рис. 6 - то же с Не—Ne лазером, имеющим значительно более узкий спектр излучения (ширина контура усиления составляет 0,03 8).

Для оценки ФРТ, согласно критерию Марешаля, выполнены расчеты Q по формуле (5) для условий, которым соответствуют функции, представленные на рис. 5 (Ь, с, d); получены значения 0,89, 0,81 и 0,26 соответственно. Значения Q, вычисленные из эксперимента при условии нормировки интенсивности по ФРТ и представленные на рис. 5а (одномодовый спектр источника), равны 0,85, 0,70 и 0,22 соответственно. Пересчет мощности сделан по току диода из графика на рис. 2.

d

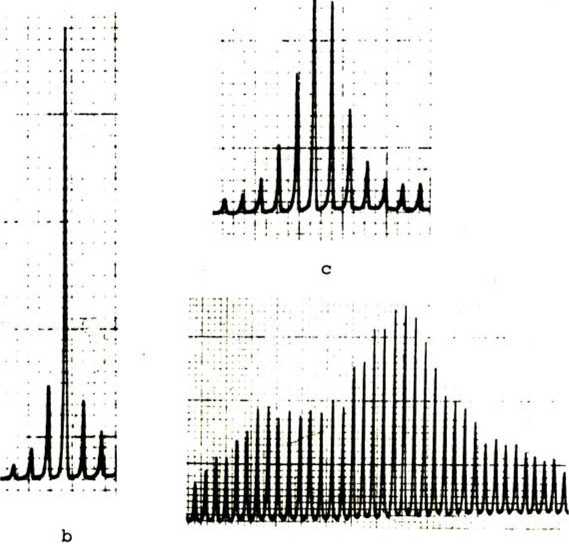
Рис. 3. Спектры излучения п/п лазера при различных режимах работы: а) ДХ = 1 A, Xmgx = 788,3 нм;

Ь) ДХ = 10,5 А, X = 788,3 нм; с) ДХ = 30 А, max          о

X = 788,3 нм; d) ДХ = 180 А, X = 789,1» нм. max                               max

Ширина спектра дана на уровне 0,1 интенсивности основной моды

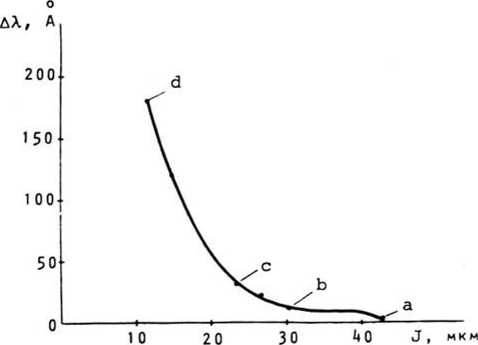
Рис. ^.. Изменение ширины спектра ДХ п/п лазера в зависимости от режима работы

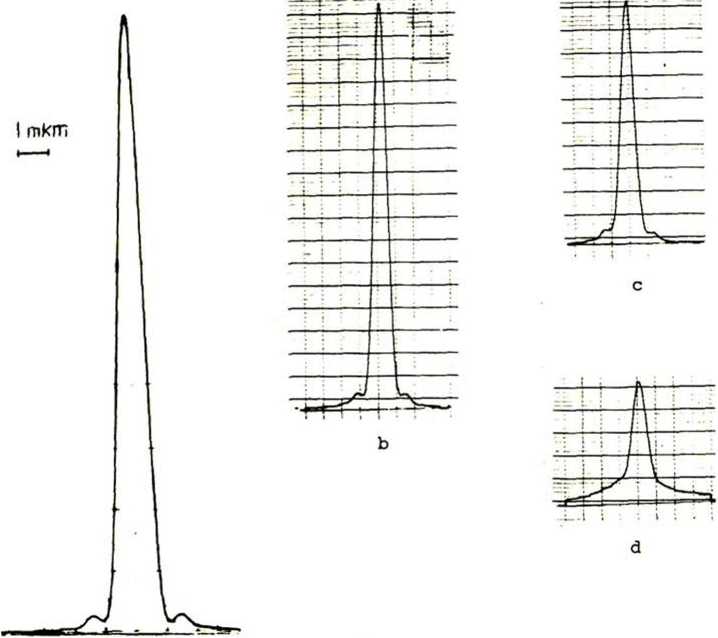
Рис. 5- Функция рассеяния точки дифракционного микрообъектива, полученная с п/п лазером при различной ширине спектра

На рис. 7 (кривая 2) показано распределение интенсивности, рассчитанное для спектра источника, приведенного на рис. Зс, по формуле [3]

I(u,v)/Io = ф2 [U2(u,v) +U2(u,v)],                                   (6)

где U, и Ua ■ функции Ломмеля. При u=v=0 формула (6) переходит в (5) .

Сравнение с безаберрационным распределением интенсивности (кривая 1) пока-о зывает, что при ширине спектра 30 А (что соответствует среднеквадратичной шири о не 11,5 А) функция рассеяния точки еще удовлетворяет критерию Марешаля. Соответ ствующая экспериментальная ФРТ (рис. 5с) имеет большую сферическую аберрацию, то есть условие Марешаля для нее не выполняется (Q = 0,70).

Экспериментальные функции отклика отличаются друг от друга тем, что уровень 1-го минимума растет по мере уширения спектра источника (рис. 8, кривая 1), размер центрального пятна при этом остается постоянным в пределах точности измерений. Кривая 2 на рис. 8 показывает интенсивность в 1-ом боковом максимуме (по отношению к центральному). Разность кривых 1 и 2 соответствует величине провала в минимуме. Для He-Ne лазера интенсивности в 1-ом минимуме и боковом максимуме отмечены точками на оси I/I . Уровень фона в 1-ом минимуме при этом наименьший - 0,8%. Для п/п лазера, работающего в одномодовом режиме (точка а на оси ДХ, ширина линии 1 А), уровень фона в 1-ом минимуме (1,65%) в 2 раза больше. При ширине спектра источника 30 А, что соответствует на рис. 8 точке с на шкале ДХ, интенсивности в 1-ом минимуме и боковом максимуме становятся одинаковыми и равными (“5%) . В расчетном распределении интенсивности (рис. 7,

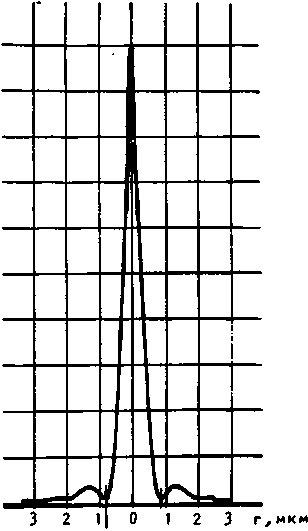
Рис. 6. Функция рассеяния точки дифракционного микрообъектива, полученная с He-Ne лазером

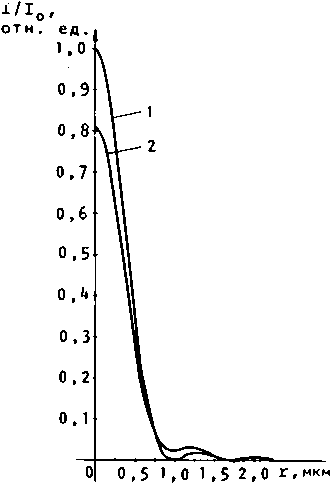
Рис. 7- Расчетное распределение интенсивности в дифракционном фокусе: 1 - безаберрационная кривая; 2 -0 при ширине спектра источника 30 А

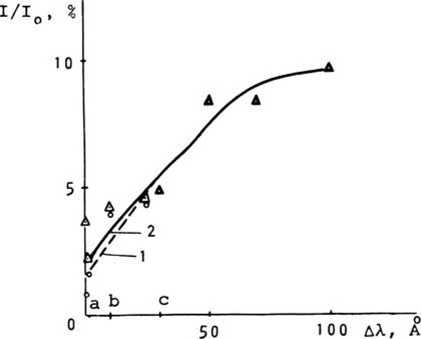
Рис. 8. Зависимость I/XQ 8 1-ом минимуме и боковом максимуме ФРТ от ширины спектра источника ДХ

кривая 2) в

1-ом минимуме фон составляет

2,5%, а интенсивность бокового макси

мума - 3,8% относительно интенсивности в центре.

При дальнейшем уширении спект

ра источника сферохроматическая аберрация возрастает настолько, что минимум и боковой максимум размываются полностью (рис. 5d) .

Критерием качества системы может служить также глубина фокусировки, которая увеличивается при уширении спектра источника за счет появления продольной сферохроматической аберрации. Сфокусированное пятно вытягивается вдоль оптической оси. На рис. 9 приведены графики падения интенсивности по обе стороны от фокальной плоскости для двух режимов работы п/п лазера, соответствующих ширине спектра о                           о

10 А (кривая 1) и 190 А (кривая 2).

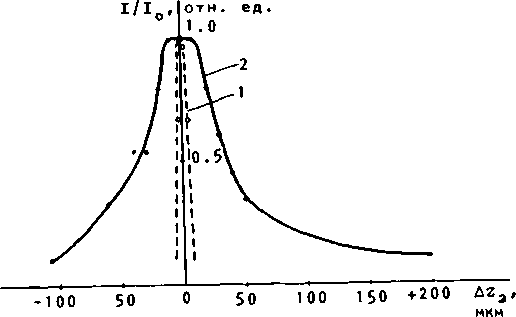
рис. 9- Распределение интенсивности вдоль оптической оси вблизи дифракционного фокуса при ширине о                           ° спектра 10 А (кривая 1) и 190 А (кривая 2)

Для кривой 1 хроматизм положения, рассчитанный по формуле

Дх2 = (ДЛ/Х)г2, равен ±2 мкм, а экспериментальное значение составило **< мкм. Для кривой 2 расчетный хроматизм положения составляет 138,5 мкм, что значительно меньше экспериментального значения. Вероятно, при таком широком спектре источника кроме хроматизма присутствует большая продольная сферическая аберрация.

Таким образом, показано, что при работе с одномодовым п/п лазером ФРТ дифракционного микрообъектива мало отличается от ФРТ при работе с He-Ne лазером.

При расширении спектра п/п лазера в ФРТ появляется фон (до 10%), увеличивающийся к центру функции, который приводит при многомодовом режиме к размытию ФРТ и исчезновению минимума интенсивности.