Влияние спектра рассеяния Доплера на величину мощности межканальной помехи OFDM - сигнала

В работе [1] рассмотрено одновременное влияние быстрых релеевских замираний и частотного рассогласования частот субканалов приема и передачи. Количественной мерой воздействия этих факторов на характеристики OFDM–сигналов служит величина межканальной помехи (МКП) между отдельными субканалами на приемной стороне OFDM [2]. В непрерывном случае, без учета дискретизации по времени OFDM–сигнал имеет вид:

N

S ( k ) = £ S k e^{jj2 n k} , 0 <  k <  T ,        (1)

k = 1

где          ^f = ^f 0 + ^{k A f} = / 0 + T;

S, =J2Ecd         + id ;

k          S m , m mr mj ;

S _k – передаваемый на k –ой поднесущей комплексный сигнал;

d _m – символ передаваемых данных с нулевым математическим ожиданием и дисперсией D ( d m ) = 1;

d_kr , d_ki – статистически независимы, идентично распределены и имеют математические ожидания равные нулю.

Постановка задачи

Постановка задачи в данной работе повторяет постановку задачи [1; 3], включая описание радиоканала с частотно–селективными быстры- ми релеевскими замираниями, который является стационарным процессом в широком смысле с некоррелированными рассеивателями на интервале локальной стационарности, превышающим длительность T, факторизуемую двумерной корреляционной функцией:

R ( т , f ) — R ( т ) - R 2 ( к — l ) ,           (2)

где R 1 ( т ) - корреляционная функция во времени;

R 2 ( к — 1 ) — корреляционная функция по частоте между поднесущими k –го и l –го субканалов.

Принимая во внимание [3], импульсная характеристика (ИХ) субканала k –ой поднесущей определяется как:

h k ( t^{, т} ) = Р к ( t ) ⁵(^т ) ,                ⁽³⁾

где 5 ( т ) - дельта функция.

Далее используем возможность представления Р_к ( t ) рядом Тейлора, введенного Bello [3], и, учитывая сравнительно небольшую скорость изменения канала на интервале длительности OFDM символа, ограничимся линейной аппроксимацией [3]:

^р к ( t ) = ^р о ( t о ) + Р к '( t о )( t ^— t о ) ,        (4)

T где t о - —.

Шум в канале – аддитивный белый гауссовский шум n ( t ) имеющий одностороннюю спектральную плотность мощности N ₀ Вт/Гц.

Для к — 1,... N Р_к ( t ) обладают идентичными статистическими характеристиками гауссова вида с нулевым средним и комплексными значениями. Принимаемый сигнал OFDM имеет вид:

N y (t) —Z Рк (t)5 (t),             (5)

к — 1

и сигнал на выходе m –го субканала с учетом (1),

(5) запишется как:

T

1 NT

7 ZH Р к ( t ) e "  j ² * ⁽ f m - f ) Ч' 5

^T к — 1 I о                                 ,

Если в канале присутствует «частотный сдвиг», то в (6) добавляется фазовый множитель:

u ( t ) — e j ^{2 na A} ft — e “ , 5 f где^a —тт;

A f

^5f - «сдвиг частот», вызванный расхождением частот передачи и приема.

Суммарный эффект, вызываемый совместным влиянием Допплеровского рассеивания и частотным сдвигом поднесущих может быть оценен по величине a , коэффициента влияния к -го субканала на m –ый субканал:

T ak1— J Рк (t )• u (t )•e " j2 n1 Afdt, T —\

здесь и далее 1 — m — к , к е 1 — N , m е 1 — N .

Определение величины коэффициента влияния

Принимая во внимание (4), (8) будет иметь следующий вид:

T а — - в (to)eete"jAftdt + kl              k0

TT

—

T

+ J Р к ( t о )( t — t о ) - e^{j 6 t}e ^{— j 2 n 1 A ft}dt .

T

Для первого интеграла в (9) из [2] можно видеть, что

, , sin n (7 — a)       , .

в к ( t о )-- — в к ( t о ) - F l .

n ( / — a )

Второй интеграл в (9) представим суммы двух интегралов: первый из них:

T 2

• 1    в к ( t о ) J t - e j ⁶' t - e ~j^' ^{A f}^ dt — T_T —

T sin ^{n ( a —} ll ) Р к ⁽ t о ) j

• 2    n ( a — / )

  •------------:---------------------------

  n ( a — / )

  
  

  —

  
  

  cos n ( a — / ) n ( a — / )

  
  

  — Р к ( t о ) - F

  
  

а второй интеграл в этой сумме:

T

7 Р к ( t о ) J — tо-е» - е"¹' - ' ^A dt — T_T

в

виде

sin n ( a — / )

• ^{— —} t о ' ^р к ⁽ t о )-- 7----- ^{— —} t о ' ^р к ⁽ t о ) ' F l .

n ( a — / )

Оценка мощности МКП, обусловленной одновременным воздействием быстрых замираний и рассогласований частот

В рассматриваемых условиях, в составе принимаемого сигнала (5) d ^ˆ _m , составляющая, соответствующая переданному сигналу d m , равна:

Cl m — d m [ P m ( t о ) ' F > + P m ( t о ) ' F ) —     (13)

• ^— t о ^{- p} m ⁽ t о ^)- F > ] ,

T что при tо — — может быть представлено как:

ˆ

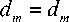
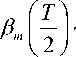
sin па па

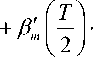
T ( .sin па 1 sin па . cos па

—I j-----+ j------

2 1 па па па па

Составляющая межканальной помехи в m –ом субканале ( МКП ) m :

N

(МКП) m = Z dk [ вк (10 )• F1+ вк( 10 )• F - (15)

к = 1, к * m

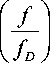
1        g cos(5) -f- e      fD

I 0 ⁽ g )

- ^в к ^{( 1} 0 ) • ¹ 0 • ^F 0 ] .

Для вычисления мощностей (13) и (14) согласно [3] используем следующие статистические свойства случайных величин в_к , в'_к , d _k : все суммируемые слагаемые в (14) и (13) являются взаимно – независимыми, так как:

• а)    для гауссовских случайных величин в_к , в к : MV At о) & to о)] 0дя^лявсех [k, т^ е 1, N . ;

• б)    произведения в _т ( t 0 ) • в _к ( t 0 ) есть произведе

ния взаимно независимых от d m • d _k величин, для которых математическое ожидание M ( d_k ) = 0.

В предлагаемой работе рассматривается выражение общего вида, как в [5], связывающее спектральную плотность мощности Допплеровского рассеивания (далее СПМ, если специально не оговорено другое) с пространственными харак-

теристиками канала, такими как направленность антенн и плотность распределения углов прихода сигналов на антенну. Легко видеть, что СПМ, рассмотренная в [1; 7; 9], полученa в случае изотроп-

ного распределения углов прихода и изотропных

характеристиках антенн. В общем случае СПМ может быть представлена в виде [2; 4]:

G f ^f 1

5 ( f ) =— f ; при V\ ^ fu ,     (16)

^{m f} DK I¹ "| ^ ।

V f u /

где f D – максимальная частота СПМ рассеяния Доплера.

Представление СПМ в виде (15), как показано в [5, 8], имеет целый ряд преимуществ перед другими формами СПМ, поскольку напрямую отображает физическую природу рассеивания Доплера и позволяет определить СПМ без использования интегралов. Если принять в качестве плотности распределения углов прихода сигналов распределение фон Мизеса–Тихонова, то получаем, согласно [6], для изотропных антенн следующую функцию

G

•

(

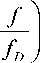
• cosh g sin ( ^ )

I

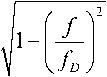
где I ₀ – модифицированная функция Бесселя 0– го

порядка;

0 - среднее значение направления углов при-

хода;

g >  0 - параметр концентрации, задающий ширину рассеяния 0 .

При g = 0 СПМ (15) соответствует закону Jakes, то есть изотропной модели Кларка [2; 4]. В общем случае (6) несимметрично относительно

f = 0.

Введем обозначение

M [| в'к (t )|2

= D .

Тогда

среднее значение оценки мощности принимаемого полезного сигнала m –го субканала запишется как:

M

d ˆ m ²

sin па 1

па 7

+ D--

( па ) 2

sin па ।

па

1 sin 2 па      ₇

+---+ cos

2 2 па

(па)

После выполнения алгебраических преобразований получаем итоговые выражения для средней мощности МКП, где а - 1 = а - ( m - к ) . Кроме этого, выполнив приведение подобных членов и обозначив нормированную величину макси-

мального значения допплеровского рассеивания β = F d /Δf , получаем итоговые выражения для средней (по субканалам) мощности MKP. Введем обозначения у = п ( а - m + к ) , следовательно.

Р

Ì ÊÏ

N

= Z

к = 1, к ^ m

п2 (а - m + к)2

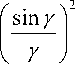
+ D--

+ •

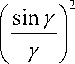
sin (2/) (2у)

Как показано в [4] для оценки мощностей полезного сигнала и МКП достаточно определить дисперсии процесса в _к ( t ) и его производных, которые для СПМ Доплеровского спектра могут быть выражены через моменты этой СПМ. В частности, для (15) имеем:

D [IPk (t )|]=1;

D [I R( t )|] = J

- 1

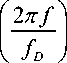
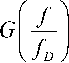
n f D

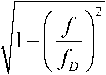
df . (20)

Оценивая влияние формы СПМ Допплеровского рассеяния на величину мощности МКП следует отметить, что аналитическое выражение дисперсии производных процесса вк (t) и, в конечном итоге, величины мощности МКП через моменты СПМ вида (16) и (17) получить весьма проблематично. Поэтому используя общее интегральное представление искомых дисперсий, как это сделано в (20), определим ее величину чис- ленным методом.

В качестве такого метода применим из [6] квадратурную формулу наивысшей алгебраической точности для интегралов вида:

1 f(x) т _ П \ k^Tdx= n § f(xk),     (21)

где ^x k – корни полинома Чебышева степени n ;

f (x ) = x2 G (x);

G (x) – определяется формулой (16).

График, иллюстрирующий СПМ в зависимо-f сти от (17) представлен на рисунке 1.

fD

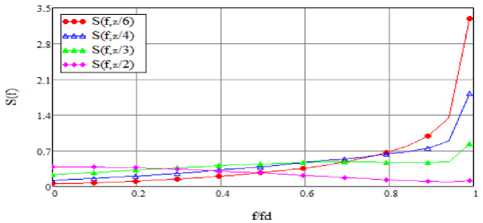
Рисунок 1. График иллюстрирующий СПМ в зависимости от f/f D

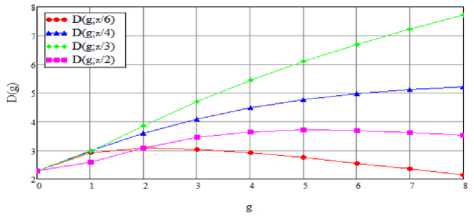
Рисунок 2. Семейство графиков иллюстрирующие значения (20), вычисленные по (21) при задании значений 6 и g

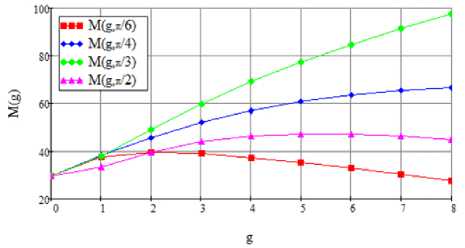
Рисунок 3. Семейство графиков иллюстрирующие

значения оценки мощности принимаемого

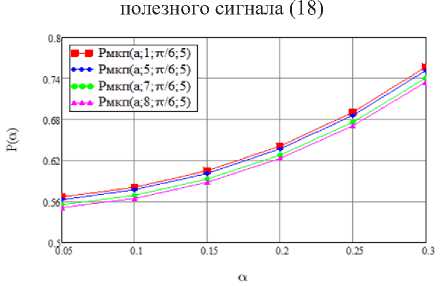
Рисунок 4. Семейство графиков иллюстрирующие значения оценки средней (по субканалам) мощности МКП (19)

Семейство графиков иллюстрирующие значения (20), вычисленные по (21) при задании значений 6 и ^g в виде семейства параметров, показаны на рисунке 2 соответственно.

Графики иллюстрирующие зависимости (18) и (19) приводятся ниже на рисунке 3 и рисунке 4 соответственно.

Оценка производительности OFDM – систем

В [1, 4] отмечается, что производительность OFDM – систем представляет собой функцию величины SNR . В результате появления МКП, мощность которой не зависит от мощности аддитивного шума в канале Pn , как правило, вводится показатель SINR, представляющий собой функ- цию отношения мощности сигнала Pñ к суммарной мощности аддитивного шума и МКП, т.е.

SINR=-----c-----, p + p 1 n T1 МКП где Pc – мощность принимаемого сигнала;

P _n – мощность аддитивного шума в канале; P МКП – мощность межканальной помехи.

Исходя из представленного соотношения (21) можно заметить, что SINR относительно SNR в OFDM – системе не подверженной Доплеровскому рассеиванию и сдвигу частот субканалов, дает ухудшение:

A = лт2|

ASNR = SNR - SINK =

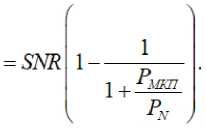
В (23) принимается во внимание, что величина мощности передаваемого сигнала равна 1, и мощность шума остается неизменной величиной. На рис. 5 и рис 6 соответственно представлены полученные результаты, рассчитанные по (22) и (23). При этом, необходимо заметить, что соотношение (22) было получено для канала с быстрыми замираниями и с нулевым частотным рассогласование при P МКП из [3].

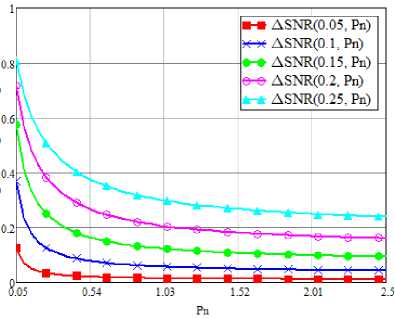
Рисунок 5. ∆ SNR в отсутствии Доплеровского рассеивания, β = 0

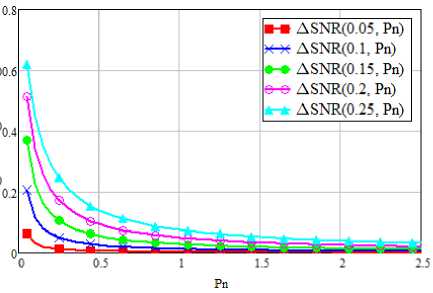
Рисунок 6. ∆ SNR для канала с быстрыми замираниями и с нулевым частотным рассогласованием

Заключение

Согласно представленным в работе результатам, можно оценить влияние быстрых релеевских замираний и частотного рассогласования частот субканалов приема и передачи в OFDM – системе. При этом, одновременное влияние данных источников, как правило, является следствием увеличения МКП и уменьшения SNR по сравнению со случаями парциального воздействия каждого источника по отдельности. Что, в свою очередь, открывает возможность определения того, насколько должны быть ужесточены требования к точности согласования частот при работе систем OFDM в каналах с быстрыми замираниями [1; 4; 10].