Влияние степени заполнения горизонтальных цилиндрических резервуаров на время их опорожнения при аварии

In the petrochemical industry for the storage and transportation of petroleum products are widely used horizontal cylindrical tanks. The scale of accidents resulting from the violation of their integrity, depend primarily on the rate of discharge of oil. Speed depends, in part, on the degree of filling of the reservoir, which determines the initial height of the liquid column. However, the regulatory impact assessment methodologies do not take into account the failures of the receptacle, that is assumed that the initial height of the liquid column is equal to the diameter of the tank. This leads to incorrect results, unnecessarily overstate or understate the effects of the disaster. In this paper, we propose a simple method of accounting for the value of degree completion*.

* Sedov D. Influence degree completion horizontal cylindrical tanks while they emptied by accident

ВЕСТНИК ВОСТОЧНО-СИБИРСКОГО ИНСТИТУТА МВД РОССИИ

При хранении и транспортировке нефтепродуктов существует опасность возникновения аварии из-за нарушения герметичности обечайки резервуаров (образование трещин, расхождение швов, износ уплотнений, расслоение биметалла, коррозия, пробои при падении резервуара с опор или обрушении каких-либо конструкций и т.д.). Тяжесть ее последствий зависит от скорости истечения нефтепродуктов на прилегающую территорию. На скорость истечения влияет не только диаметр аварийного отверстия, но и степень заполнения резервуара ε, определяемая технологическим регламентом (она определяет начальную высоту столба жидкости Н0, от которой зависит скорость истечения). Если для вертикальных резервуаров постоянного сечения Н0 определяется просто (объем жидкости в резервуаре Vж = εV, где V – объем резервуара, следовательно, Н0 = εНрез, где Нрез – высота резервуара), то для горизонтальных цилиндрических резервуаров, у которых сечение по высоте не постоянно, формулу Н0 = εНрез не применяют. Поэтому зачастую при оценке последствий аварии степень заполнения ε не учитывают совсем, то есть принимают, что Н0 равно диа- метру резервуара. Это, естественно, приводит к некорректным результатам, необоснованно завышающим или занижающим последствия аварии. В настоящей работе предлагается новый способ учета величины ε.

Время опорожнения горизонтального цилиндрического резервуара определяется по известной формуле (см., например, [1]):

16 LD ²

3 µ ₀ π d_о ² _тв 2 g

где L – длина резервуара;

D – диаметр резервуара;

µ 0 – коэффициент расхода через аварийное отверстие (0,62 для отверстия в тонкой стенке);

d отв – диаметр аварийного отверстия в днище резервуара (возникновение отверстия в днище – наиболее опасный вариант);

g – ускорение свободного падения.

Однако выражение (1) применимо в случае, когда резервуар заполнен на 100 %. При частичном заполнении резервуара необходимо изменить граничные условия дифференциального уравнения, из которого получена формула (1) (см. [1]):

где Н – высота столба жидкости в резервуаре.

В левой части уравнения (2) – объем нефтепродукта, вытекшего из резервуара за время dτ, в правой – объем резервуара, освободившийся от нефтепродукта за это же время.

Уравнение (1) получено из (2) при следующих граничных условиях:

в начальный момент времени (при τ 1 = 0) высота столба жидкости равна диаметру резервуара ( Н 1 = D ), в момент опорожнения (при τ 2 = τ оп ) высота столба Н 2 = 0.

В случае же частичного заполнения при τ 1 = 0 начальная высота столба Н 1 будет равна не D , а некоторой величине Н 0 <  D . После интегрирования (2) в новых границах получаем выражение для времени опорожнения частично заполненного горизонтального цилиндрического резервуара:

3 /            X³

16 L D ² - ( D - Н 0 ) 2

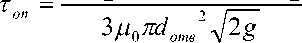
Величина Н0, как правило, неизвестна и зависит только от степени заполнения ε резервуара, которая задается технологическим регламентом. Зависимость Н0 = f(ε) можно получить из уравнения (2), записанного в dV = -2 L^H (D - H)dH,       (4)

где dV – объем нефтепродукта, вытекшего из резервуара за время dτ .

В начальный момент времени Н 1 = Н 0 , а объем вытекшего нефтепродукта V 1 = 0. В конечный момент времени Н 2 = 0 , а V 2 = V ж ( V ж – объем жидкости в резервуаре). Интегрируя (4) в данных границах, получаем:

0               Н 0

J dV = - 2 L j V H ( D - H ) dH ;

V ж             0

Н 0

К ж = 2 L J V DH - H²dH . (5)

Н 0

Интеграл J \DH - H2 dH явля-

ется интегралом вида J \ a + bx - cx ² dx (см., например, [2]), решение которого выглядит следующим образом:

виде:

г I ;       2",     2 cx - b /    :        2" b ² + 4 ac     .   2 cx - b

I V a + bx - cx dx =------- a+ + bx - cx +-- .— arcsin .      ^ + const.

^J                     4 c                    8д/ _c³         bb + 4 ac

Следовательно, искомый интеграл составит:

J V DH - H² dH = ^{2 H 0 D} DH₀ - H_o² 0 ⁴

, D ²    . 2 H_o - D . nD ²

+-- arcsin-- 1-- ,

8          D 16

а выражение (5) примет вид:

Vж

= L [ 2 H ⁰   D DH о - H о

V ²

D ²    . 2 H _o - D   n D ² )

+-- arcsin----⁰-- 1--

4          D 8 J

.

Так как К ж = e V = e

π D ²

L , то вместо (6) получаем:

£ =

DH 0

—

H 0

+— arcsin π

2 H 0 - D

D

+ 0,5.

Выражение (7) и есть зависимость Н 0 = f ( ε ) (в явном виде выразить Н 0 не удается).

На примере горизонтального цилиндрического резервуара размерами L = 5 м и D = 2,5 м построен график данной функции (рис. 1). Из рисунка видно, что график функции (7) можно приближенно заменить прямой линией:

H о = £ D (8)

(прослеживается аналогия с вертикальными резервуарами, для которых Н 0 = ε Н рез ). Как будет показано ниже, данная замена дает все же более точные результаты, чем расчеты, не учитывающие ε .

По графику функции (7) (см. рис. 1) определяем, что если ε = 0,9, то Н 0 = 2,15 м. Теперь по формуле (3), зная диаметр аварийного отверстия d отв , можем найти время опорожнения резервуара.

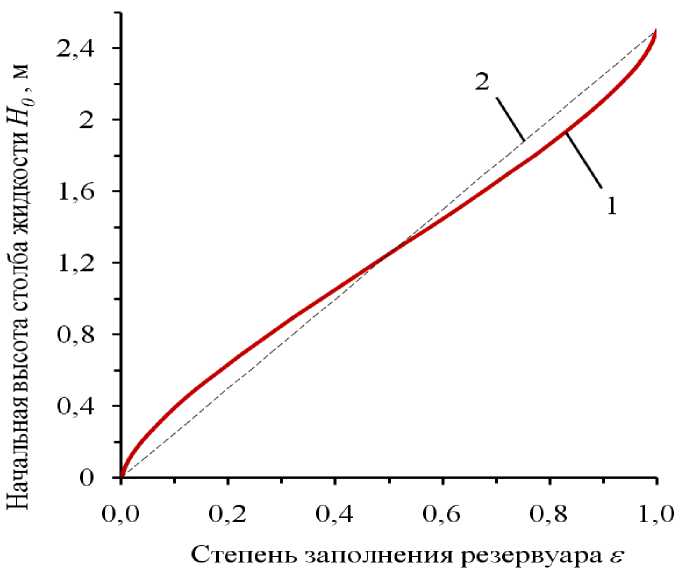
Рис. 1. Зависимость начальной высоты столба жидкости Н₀ от степени заполнения s горизонтального цилиндрического резервуара: 1 -функция (7);

2 - зависимость Н₀ = s D

Рассмотрим наиболее часто образующиеся при авариях отверстия ( d отв = 0,03…0,1 м [3]). Так, при d отв = 0,04 м нефтепродукт вытечет из резервуара через 2 ч. Расчеты же без учета ε , то есть по формуле (1), дают завышенный результат: 2,12 ч. Результаты с учетом (8) более точны: 2,06 ч.

На рис. 2 показан график зависимости времени опорожнения резер- вуара (3) от степени его заполнения при dотв = 0,04 м. Как видно из рисунка, если степень заполнения уменьшается, расхождения в результатах заметно увеличиваются. Например, при ε = 0,8 (Н0 = 1,86 м) время выхода нефтепродукта по формуле (3) с учетом зависимости (7) составляет 1,85 ч. Если вместо (7) использовать (8), то получается 1,93 ч.

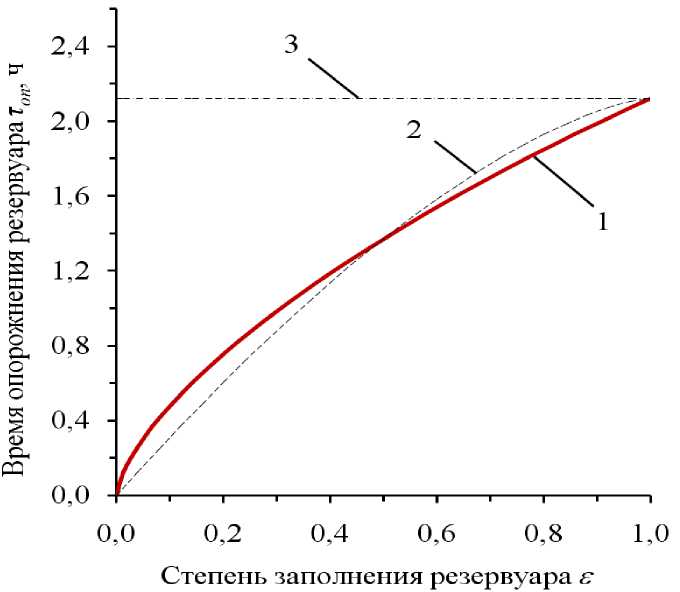
Рис. 2. Зависимость времени опорожнения резервуара (3) от степени его заполнения (при d отв = 0,04 м): 1 – с учетом зависимости (7);

2 – с учетом приближенной замены (8); 3 – без учета ε , зависимость (1)

На рис. 3 показан график зависимости времени опорожнения (3) от степени его заполнения ε при различных значениях dотв. Из рисунка видно, что если не учитывать ε, то расхождения в результатах увеличива- ются с уменьшением dотв. Например, при ε = 0,9 время опорожнения резервуара с учетом (7) для отверстий диаметром 0,1 м, 0,05 м и 0,03 м соответственно составляет 0,32 ч, 1,27 ч и 3,53 ч. Без учета ε, то есть по формуле

(1) время опорожнения равно 0,34 ч, 1,36 ч и 3,77 ч.

Однако относительная ошибка вычислений (в %)

о    Топ - Топ (£)| от = J---------------1

τ _оп ( ε )

•100

( τ оп – время опорожнения либо без учета ε , либо с использованием приближения (8); τ оп ( ε ) – время опорожнения с учетом ε по зависимости (7)) от размера отверстия не зависит и определяется только точностью учета степени заполнения (рис. 4).

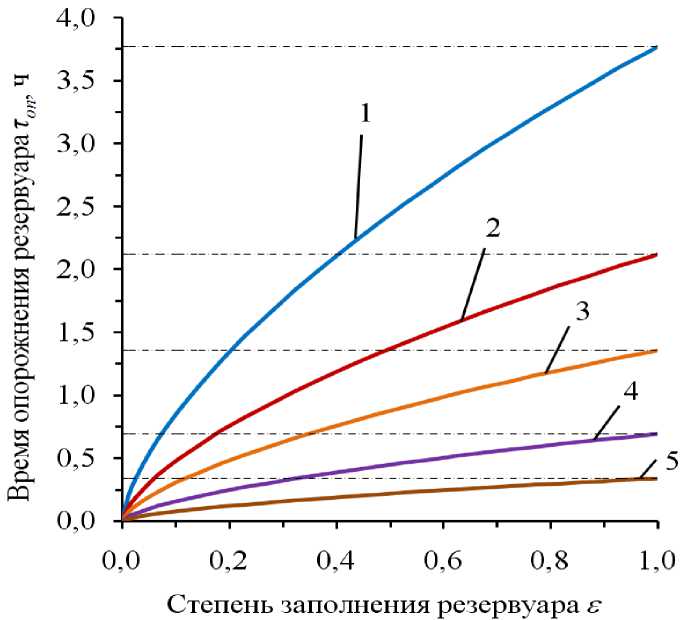
Рис. 3. Зависимость времени опорожнения резервуара от степени его заполнения при различных диаметрах аварийного отверстия: 1 – 0,03 м; 2 – 0,04 м; 3 – 0,05 м;

4 – 0,07 м; 5 – 0,1 м; пунктиром показаны результаты соответствующих расчетов без учета ε , по формуле (1)

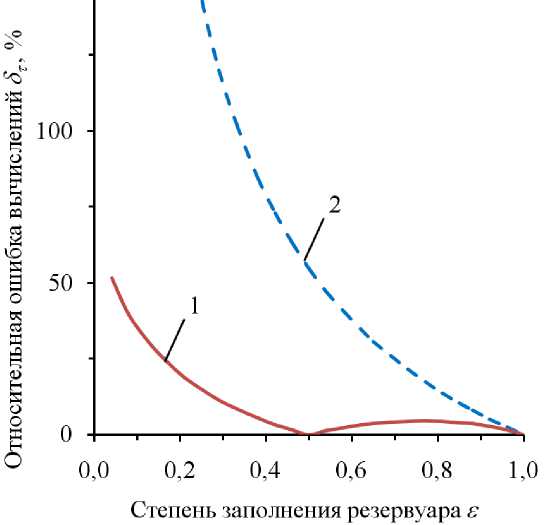
Рис. 4. Относительные ошибки вычислений времени опорожнения горизонтального цилиндрического резервуара: 1 – по формуле (3) с учетом приближенной замены (8);

2 – без учета ε , по формуле (1)

Как видно из рис. 4, относительные ошибки расчетов с использованием замены (8) не превышают 4,5 % при ε = 0…0,5. При меньших ε (менее 0,4) погрешности превышают 5 % и быстро увеличиваются. Относительная погрешность вычислений без учета ε уже при ε = 0,9 достигает 7 %, при ε = 0,8 она составляет 14,7 %, а при ε = 0,5 составляет 54,7 %.

Все же при оценках последствий аварий большее значение имеет абсолютная ошибка. Ведь просчет всего на несколько минут может увеличить последствия проектной аварии (например, избыточного давления взрыва) в разы.

Увеличение абсолютной ошибки при уменьшении размера отверстия и степени заполнения резервуара наглядно прослеживается по графикам на рис 5.

Как видно из рис. 5, при больших аварийных отверстиях абсолютная ошибка расчетов без учета степени заполнения невелика и соизмерима с погрешностью при использовании приближенной замены (8), что объясняется большей скоростью истечения нефтепродукта.

Так, при образовании в рассматриваемом резервуаре пробоя с диаметром отверстия d отв = 0,1 м время его опорожнения без учета степени заполнения при ε = 0,9…0,8 оказывается завышенным на 0,02–0,04 ч.

При малых значениях d отв и снижении ε абсолютная погрешность, напротив, резко увеличивается. Так, если d отв = 0,03 м, то при ε = 0,9 время опорожнения резервуара становится больше на 0,23 ч, а при ε = 0,8 время опорожнения будет завышено на 0,48 ч.

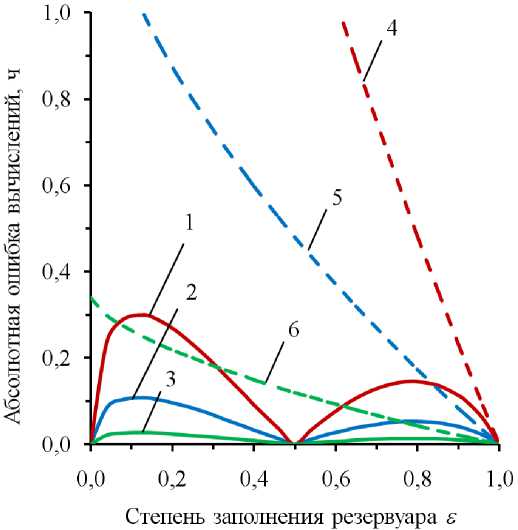
Рис. 5. Абсолютные ошибки вычислений времени опорожнения горизонтального цилиндрического резервуара при различных диаметрах аварийного отверстия: 1 и 4 – 0,03 м; 2 и 5 – 0,05 м; 3 и 6 – 0,1 м; сплошная линия – по формуле (3) с учетом приближенной замены (8); пунктирная линия – без учета ε , по формуле (1)

Таким образом, при исследовании влияния степени заполнения горизонтальных цилиндрических резервуаров на время их опорожнения получена точная аналитическая зависимость, которая позволяет избежать завышения или занижения теоретических последствий аварий. Обосновано применение приближенной зависимости Н0 = εD, которая, тем не менее, дает более точные результаты, чем расчеты без учета степени заполнения ε. На примере горизонтального цилиндрического резервуара объемом 25 м3 показано, что неучет данной величины приводит к тому, что при наиболее распространенных размерах аварийных отверстий (0,03–0,1 м) и степенях заполнения резервуаров (0,9–0,8) время опорожнения завышается на 0,23–0,48 ч, относительная ошибка расчетов составляет 5,1–14,7 %. При увеличении объема резервуаров погрешность будет уменьшаться.