Влияние структурной анизотропии на устойчивость композитной цилиндрической оболочки при осевом сжатии

Типичной структурой стенки композитной цилиндрической оболочки является система слоев одинаковой толщины, армированных под углом к образующей цилиндра. Как правило, слою с углом армирования +ф соответствует такой же слой с углом армирования -ф (рис. 2).

Рис. 2. Схема армирования стенки оболочки

Подобные слоистые структуры принято считать ортотропными. Однако это утверждение является справед ливым только в том случае, когда число слоев, формирующих стенку оболочки, велико. При определенном отношении толщины стенки к толщине слоя структура стенки, состоящая из слоев с углами армирования ±ф, должна рассматриваться как анизотропная. Для доказательства этого утверждения выполним анализ жест-костных параметров в физических соотношениях, записанных в характерном для анизотропных оболочек виде:

N а ^— B 11 ^Е а ⁺ B 12 ^Е р ⁺ B 13 ^Е ар ^{+ C} 11 % а ^{+ C} 12 % р ^{+ C} 13 % ар ,

N р ^{— B} 21 ^Е а ^{+ B} 22 ^Е р ^{+ B} 23 ^Е ар ^{+ C} 21 % а ^{+ C} 22 % р ^{+ C} 23 % ар ,

N ар ^{— B} 31 ^Е а ^{+ B} 32 ^Е р ^{+ B} 33 ^Е ар ^{+ C} 31 % а ^{+ C} 32 % р ^{+ C} 33 % ар , Q)

M а ^{— C} 11 ^Е а ^{+ C} 12 ^Е р ^{+ C} 13 ^Е ар ⁺ D 11 % а ⁺ D 12 % р ⁺ D 13 % ар ,

M р ^{— C} 21 ^Е а ^{+ C} 22 ^Е р ^{+ C} 23 ^Е ар ^{+ D} 21 % а ^{+ D} 22 % р ^{+ D} 23 % ар , M ар ^{— C} 31 ^Е а ^{+ C} 32 ^Е р ^{+ C} 33 ^Е ар ^{+ D} 31 % а ^{+ D} 32 % р ^{+ D} 33 % ар ^.

ЗдесьNа, Nр,Nар -мембранныеусилия; Mа, Mр -изгибающие моменты; Mар - крутящий момент; Еа, Ер, Еар - компоненты мембранной деформации; % а, % р - компо ненты изгибной деформации; %ар - компоненты крутиль ной деформации; B, C, D - мембранные, смешанные и изгибные жесткостые параметры стенки оболочки.

Жетскостные параметры стенки оболочки определя ются по формулам [1] hhh

B mn — j А mn d Y, C mn — J Amn Y d Y, Dmn — J Amn Y 2 d Y, (2) hhh

-- -- -- 222

( mn — 11,12,13, 21, 22, 23, 31, 32, 33 )

где h - толщина оболочки; A_mn - коэффициенты жесткости слоев. Для слоя, армированного под углом ф к оси а, величины A_mn определяются следующим образом:

А 11 = E 1 c ⁴ + E ₂ s ⁴ + 2 E ₁₂ c ² s ²,

A ₁₃ = c s [ E 1 c ² - E ₂ s ² - E ₁₂ ( c ² - s ² )]

A ₂₃ = cs [ E 1 s ² - E ₂ c ² + E ₁₂ ( c ² - s ² )]

A j₂ — E j P j₂ + ( E j + E 2 - 2 E 12 ) c²s ², A 22 — E 1 s ⁴ + E ₂ c ⁴ + 2 E 12 c² s ², A 33 — ( E 1 + E 2 - 2 E 12 Й 12 ) c ² s ² + G j2 ( c ² - s ² ) ², (3)

A - 4    4 = 4    4 = 4 FG

21    ^12,   ^31    ^13,    ^32    ^23,    -^12 "^1 ^12 +

1                     ,        ^2,

¹ P 12 P 21              ¹ P 12 P 21

c — cos ф,      s — sin ф.

Здесь E 1 , E ₂ - модули упругости в направлении армирования и направлении, перпендикулярном ему; G₁₂ - модуль сдвига; р₁₂, ц₂₁ - коэффициенты Пуассона.

Коэффициенты жесткости A mn рассматриваемой слоистой структуры (см. рис. 2) являются кусочно-постоянными функциями координаты у. Выполняя в формулах (2) интегрирование по слоям для жесткостных параметров В , C , D , получим выражения

^{д 2} M а + 2 ^{д 2} M 21 । ^{д 2} M 1 д а ² д а д р д р ²

N 1 + ^N 2 | 4 = 0 ; (10) R д а

В = h ( A ( — ) + A ( + ) ) C = ( - 1 ) 2 h ²- ( - A » + A И mn 2 mn m"mn Л mn          4 k mn m^mn ,

D - h    ^{(-)    (+)}

D mn 24 ⁽ A mn ⁺ A mn ) ,

геометрические соотношения:

_ д2 w     _ д2 w      _ о д2 w z2 "-да2", z 1    др, z21     дОдр;

уравнение совместности деформаций

( mn = 11,12,13, 21, 22, 23, 31, 32, 33), где k- число слоев; A mn ) - коэффициент жесткости слоя с углом армирования -ф; A mn ) - коэффициент жесткости слоя с углом армирования +ф.

Вернемся теперь к формулам (3), определяющим для заданного материала зависимость коэффициентов жесткости от угла армирования. Подставляя в них углы -ф и +ф и сравнивая величины A ^- и A mn¹ , получим следующие соотношения:

A m — n " A mn ) ,   если mn = 11, 12, 21, 22, 33; ₍₅₎

A mn =- A mn ) , если mn = 13, 23, 31, 32.

Преобразуем далее равенства (4). С учетом соотношения (5) будем иметь

B = fhAm+n ’, если mn = 11,12,21,22,33, mn |0, если mn = 13,23,31,32,

д ² _е 2 + 9^ -д^ - 2 д ² w д р ^{2 +}д а ² д а д р R д а ²

В уравнениях (9).. .(12) не оговоренные ранее обозначения имеют следующее значение: w - прогиб оболочки, N “ - мембранное усилие, соответствующее докри-тическому состоянию оболочки. Примем, что исходное напряженное состояние является безмоментным. Тогда для мембранного усилия N ® будем иметь

N 2 "- T . (13)

В соответствии с традиционной схемой решения задач устойчивости цилиндрических оболочек в рамках технической теории введем функцию напряжений f ( а,р ) по формулам

д² f ,,   д² f

N ² др ² , N ¹    д а ² , N ²¹

^^^^^^в

д ² f да др

.

С mn

k 22

__ ( - 1 ) ² h-A mn ’, если mn = 13, 23, 31, 32,

^{2 k}                                     (6)

0, если mn = 11, 12, 21, 22, 33,

D mn

"[ 12

h 3 п(+ ) mn ,

если mn = 11,12,21,22,33,

Подстановка усилий (14) в уравнение устойчивости (9) приводит к их тождественному удовлетворению. Получим разрешающую систему уравнений, содержащую в качестве неизвестных прогиб оболочки и функцию напряжений. Первоначально разрешим физические соотношения (7) относительно мембранных деформаций. В результате преобразования получим

0, если mn = 13,23,31,32.

Подведем некоторые итоги. В физических соотношениях (1) подчеркнутые члены в соответствии с равенством (6) обращаются в ноль. Однако смешанные жесткости C ₁₃, C ₂₃, C ₃₁, C ₃₂ для рассматриваемой слоистой структуры отличны от нуля. Их величина, как это следует по формулам (6), обратно пропорциональна числу слоев k . Только при достаточно больших значениях k смешанные жесткости C ₁₃, C ₂₃, C ₃₁, C ₃₂ можно рассматривать как малые величины, а слоистую структуру стенки - как ортотропную. Таким образом, физические соотношения (1) принимают следующий вид:

^N а "  ^ВИ^£ а ^{+ В} 12 ^£ р ^{+ C} 13 ^X ар ,       ^N р "  ^B 21 ^£ а ^{+ В} 22 ^£ р ^{+ C} 23 ^X ар , (_)

^N аР "  ^В 33 ^£ аР ^{+ C} 31 Z а ^{+ C} 32 X Р ,

^M а = ^C 13 ^£ аР ⁺ D 11 X а ^{+ D} 12 X р .     ^M р = ^C 23 ^£ аР ^{+ D} 21 X а ^{+ D} 22 X р . („)

^M аР "  ^C 31 ^£ а ^{+ C} 32 ^£ р ^{+ D} 33 ^X аР '

Оценим влияние смешанных жесткостей C ₁₃, C ₂₃, C ₃₁, C ₃₂ на несущую способность оболочки. Воспользуемся для решения задачи устойчивости цилиндрической композитной оболочки уравнениями технической теории. В рамках этой теории система уравнений, описывающая потерю устойчивости оболочки, помимо физических соотношений (7), (8) включает линеаризованные уравнения устойчивости:

Э N д N       д N   д N

' ² +---± = 0,     —21 +--- 1 = 0,     (9)

д ад р , д ад р ,

Е « = E 11 N « + E 12 N р

^Е р "  ^E 21 ^N « ^{+ E} 22 ^N р

^Е _Нр "  ^E 33 ^N _нр

-

где

E = B 22 ;

¹¹ B ;

E 22 "

B 11 B

E 33 "

B ₁₁ C ₂₃

F 23 "

^^^^^^в

B

-

-

^F 31 X 2

^F 13 ^X «р ,

F 23 ^X «р ,

-

F 32 X р ,

E 12 "  E 21 "

1 B 33 ^;

B 21 C 13 ;

^^^^^^в

B 12 B ^;

B 22 C 13

F 13 =------

B 12 23

B

;

С

C ₃₁

FA

C

F 32 = ^32 ;   b = b_ub 22

B 33

B ₃₃

^- B 122 .

;

Исключим далее мембранные деформации из физических соотношений (8). Подставляя (15) в (8), будем иметь

^M a ^G13 ^N ар ^{+ H} 11 X а ^{+ H} 12 % р , ^M р "  ^G 23 ^N ар ^{+ H} 21 % а ^{+ H} 22 % р , ^M ар "  ^G 31 ^N а ^{+ G} 32 ^N р ^{+ H} 33 % ар ,

где

G 13 "  ^C 13 ^E 33 ; ^G 23 "  ^C 23 ^E 33 ; ^G 31 "  ^C 31 ^E 11 ^{+ C} 32 ^E 21 ; ^G 32 "  ^C 31 E 12 ^{+ C} 32 ^E 22 ;

^H 11 " ^D11 ^{- C} 13 ^F 31 ; ^H 12 "  ^H 21 " D 12 ^{- C} 13 F 32 ;                             ⁽¹⁸⁾

^H 22 " ^D 22 ^{— C} 23 F 32 ; ^H 33 " ^D 33 ^{— C} 31 F 13 ^{— C} 32 ^F 23^.

Затем, последовательно подставляя (17), (15), (14) и (13) в уравнения устойчивости (10) и совместности деформаций (12), получим

p д ⁴ f ₊          ) д ⁴ f д ⁴ f

E ¹¹ др ^{4 +(} 2 E ^{12 +} E ³³ ) да ² др ^{2 +} E ²² да ^{4 +}

^{+ (} 2 F 13   F 32 )

⁽ 2 G 32   G 13 )

д ⁴ w дадр ³ д ⁴ f

⁺ ( 2 F 23   F 31 )

-

да ³ др

^{+ ( 2 G} 31 - ^G 23 }

д4 w 1 д2 w _ 0 да3др - R 10? = , д 4 f    1 д2 f

--

-

да др ³ R да ²

-

H 11 ^ w + 2 ( H 12 + 2 H 33 ) ^24 ^ 2 + H 22 да                да др

д ⁴ w

др ⁴ _

-

T ^ w = 0. да ²

Предполагая, что на краях оболочки выполняются условия шарнирного закрепления, представим решение уравнений (19) в виде тригонометрических рядов то w = £ (wnm cosX n P + wnm sin X n P)sin X m a, m=1 то f = £ (/„m COsX n P + f(m sinX n P )sinX m a,    (20)

m = 1

(n = 2, 3, .., то), где X m = mл ,1; X n = n/R; m - число полуволн вдоль образующей оболочки; и - число волн по окружности оболочки; f(v), w(v) (v = 1, 2) - неизвестные числа.

mn mn

Подставляя разложения (20) в равенства (19), получим однородную систему линейных алгебраических уравнений:

a nm^f nm ^{+ —} m' a nm f n^ R

то

w(1) _ V b t  w(2) = о, nm          nm1 mm1 nm1      ,

m ] =1

то

w⁽²⁾— X b I w⁽¹⁾ = 0, nm         nm ₁ mm ₁ nm ₁       ,

где

( 1 ) c w nm nm

m 1 =1 то

-

—/⁽¹⁾ - У d I /

R nm        nm ₁ mm ₁

c w ^{( 2 )} nm nm

m^

то

nm ₁

- t x m w nm = o,

-

-m -/⁽²⁾ - У d I /

R nm        nm ₁ mm ₁

m^

nm ₁

- t - m w nm = o,

( m = 1, 2, ...,то, n = 2, 3, „.,то )

I mm ₁

^a b

mn

nm ₁

= E _ПХ 4 + ( 2 E 12 + E 33 ) - n X m + E 22 X 4m ;

r nm dnm1

= X n X m 1 [ ( 2 F 13- = H _nX ⁴ m + 2 ( H 1 = X n X m 1 [ ( 2 G 32

- F 32 ) X n + ( 2 F 23 - F 31 ) X m , ] 12 ⁺ 2 H 33 ^{) -} n ^- m ^{+ H} 22^X „ ^;

-

2l sin К a cos К a d a = m        m1

l ₀

G 13 ) - m , + ( 2 G 31 - G 23 ) - n ] 0, если m ± m 1 четно,

4 m

--------, если m ± m 1 нечетно, л m 2 - m 1

Исключим из уравнений (21) неизвестные f m " ) ( у = 1, 2 ) . В результате преобразований получим следующую систему уравнений:

то p w(1) — X r pmn nm       nmm1

то

где

m 1 =1

то p w(2) + X S'   w1

pmn nm        nmm1 n m1=1

w"^ m ] - £ s, ^m 1 ^{= 1}

то

,^{(1 )} - У nm ₁

m 1 =1

'     w ^{( 2 )}

nmm ₁ nm ₁

r    w ^{( 2 )}

nmm ₁ nm ₁

- Tw nm = 0,

- Tw nm ’ = 0, (23)

( m = 1, 2, ..., то, n = 2, 3, „.,то ),

enm pnm 2 ;

^X m

4m- nm nm            ;

R ² a_nm

г nmm1

g nmm ₁

;

S

nmm ₁

h n mm ₁

- ^;

h

n m m ₁

I mm ₁ R

' ^X m b m 1

+

^{X m} 1 b nm

g nm   ^bnm_x^knmm_} ^;

V

а а nm         nm1

то nm2

mm   ^£        mm 2 m 2 m 1

m 2 =1 a nm 2

Удержим в бесконечных рядах (23) i членов по продольной координате а и] членов по окружной координате р . Перепишем систему (23) для выбранных i и] в виде матричных уравнений

( P n - R n М- S n W ( ^{2 )}- T W ®= 0, S n W ^{( 1 )}+ ( P n - R n ) W ( ^{2 )}- T W ( ^{2 )}= 0, ( n = 2, 3, „., j ),

где

R

n

W? =

" w ^(v)

)

w j¹

r;P n =^

p n 1 0

0 p n 2

;

r n 11

Г n 21

г n12

г n22

г n1i

г n2i

^; s n

s n 11

s n ₂₁

^sn 12

s n ₂₂

г ni1

г ni2

г n ii

( v = 1,2 ) .

pni

sn1i sn2i

^; (26)

s n _i1

s n _i2

s n _ii

Объединяя уравнения (26), окончательно получим

( Z n -T E)W„ = 0, ( n = 2,3, _ , j ),        (27)

где

⁽¹⁾1             -R -S 1

^w" =ы4 ^z" =1 ⁿs ⁿ p-r [•      (²⁸)

L n t n n n

Здесь E - единичная матрица. Критическая нагрузка соответствует минимальному собственному числу однородной системы уравнений (27).

В качестве примера определим критическое усилие Т для слоистой оболочки, изготовленной из углепластика типаР313 [2]. Радиус оболочки-0,5 м, длина - 1 м, толщина - 0,002 м. В расчетах варьировалось число слоев к и угол армирования ф. Рассматривались структуры стенки оболочки (см. рис. 2) с к = 2,4, 6,10,20. Угол ф изменялся от 0° до 90°. При решении в рядах (20) удерживалось 50 членов по продольной координате и 20 членов по окружной координате (рис. 3).

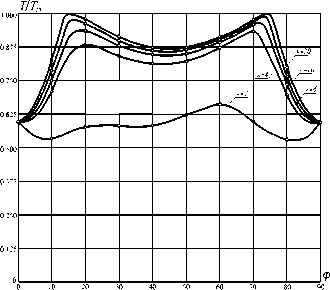
Рис. 3. Изменение величины Т / Т ₂₀ ( Т _г0 - максимальное критическое усилие оболочки с к = 20) в зависимости от числа слоев и угла армирования

Число слоев к , а значит, и смешанные жесткости C ₁₃, C ₂₃, C ₃₁, C ₃₂ оказывают значительное влияние на величину критического усилия. Только при к = 20 критическое усилие практически совпадает с критическим уси-

лием, найденными по расчетной модели, в которой структура стенки является ортотропной.

Таким образом, анизотропия стенки оболочки, у которой структура армирования традиционно считается ортотропной, должна, как показал приведенный выше анализ, учитываться при расчете критических усилий.