Влияние структурных параметров и напряженного состояния на ползучесть цементных композитов

Предельные деформации гпр при осевом сжатии или растяжении можно определить из интегрального уравнения ползучести, предложенного В. М. Бондаренко [1; 2]:

£пр(О = SM («(t))

1 EMco

t

d

j Sn (^t)) fa c(t, to)dt, t0

где г - полные деформации в момент наблюдения t; t₀ - время приложения напряжения a(t) ;

S_M , S_n - функции напряжений для мгновенных и запаздывающих деформаций; E M (t) -начальный модуль упругости; c(t, t 0 ) - мера ползучести.

Рассмотрим ползучесть образца композита, контактирующего с агрессивной средой и находящегося под действием центрально сжимающей нагрузки P . Предполагаем, что реологические параметры E₀(c), Е д (с), т(с) зависят от концентрации (с) агрессивной среды. Тогда, согласно [3], для случая переменных свойств материала уравнение ползучести в линейном приближении имеет вид:

Е0(с)т(с)ё+ Ед(с)г = и + т(с)а,                       (2)

где  Е0 - начальный модуль упругости; Ед - длительный модуль упругости; т - время релаксации.

При неравномерном распределении концентрации жидкости по площади поперечного сечения образца для решения уравнения (2) воспользуемся методом усреднения реологических параметров (рис. 1).

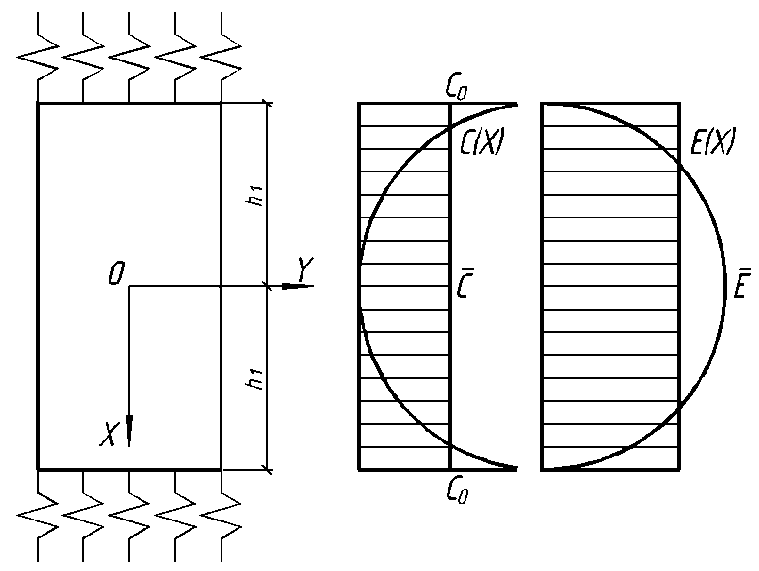
Рис. 1. К расчету ползучести методом усреднения в зависимости от концентрации по высоте сечения: h 1 + h₂ - высота поперечного сечения экспериментального образца;

С(Х ) - эпюра изменения концентрации агрессивной среды в объеме образца при двустороннем проникновении агрессивной среды;

Е (Х) - эпюра изменения прочностных свойств материала образца при двустороннем проникновении агрессивной среды.

Уравнение ползучести (2) после усреднения реологических параметров примет вид:

Е0Т £ + Ед £ = (7 + ТО .

Если в момент t = 0 концентрация агрессивной среды в материале равна нулю (с = 0), то решением уравнения (3) является функция

t

(т

£(t) = ^+ I К (t,t0)dt0.

Едт

Д0

Предполагая, что начальные значения Е₀ (с_Н) и т(с_Н) не зависят от концентрации среды, и выражая изменение Е д по площади поперечного сечения элемента линейной или экспоненциальной функциями, находим ядро уравнения

К (t,t0)=    S0     1

Е0 (сН)т \

—

^Е Д

Е 0 ⁽ С н )

ехр (- h^ dt»)j

В формуле (5) среднее значение длительного модуля деформации равно

Ед = fQE (t,x)dx = ЕоСн D(Wc),                      (6)

где D(WC) — деградационная функция жесткости, определяемая в общем случае из соотношения:

D(W c ) =

Де (t,x,y)dxdy I Д

F(t)                      '  ^(0)

Е (t0,x,y)dxdy

С учетом выражения (6) и ядра уравнения (5) деформации ползучести будут определяться из соотношения:

+ =?f Г1 — D(WC) exp (- f DWC) dt0)) dt0. (8)

ЕоЫ D(Wc)  ЕоШ t (c_h)J\         \ о ^Ы //

При действии сжимающих напряжений деградационная функция D(W) зависит от скорости переноса жидкости в объем и химического взаимодействия материала с агрессивной средой. Основной характеристикой скорости переноса жидкости в пористой среде является обобщенный коэффициент диффузии D, определяемый формулой [4, 5]:

D =

Dm +

4 R2^

192 Dm .

Зависимость усредненного значения радиуса пор R от уровня сжимающих напряжений имеет вид уравнения:

R2 =    ПОт exp{—ас} ^ R2 exp{—а-}.

4л AN             ^{0 r}

Тогда выражение, определяющее деградационную функцию D(W) при к₂ = 1; к_т = 1; к 1 = E(t)/E(0), можно записать в виде:

D(W) = 1-

2k(0j(Dm + (4 RO ^m/192 Dm) expt-ao) t

(- El)  ■"■

h

По результатам проведенных исследований получены зависимости, позволяющие аналитически описать процессы ползучести, происходящие в материале конструкций на основе цементных вяжущих под действием сжимающих напряжений и агрессивных сред. Приведенные зависимости целесообразно использовать для описания процессов деградации цементных композитов, а также прогнозирования поведения и срока службы строительных конструкций.