Влияние структуры на механические свойства двухфазных композиционных материалов

Practical application of space reinforce composite materials causes the necessity of forecasting the mechanical properties of such materials. In the article is introducing the method of forecasting of the Hung module and Poisson coefficient for composite materials which are reinforced by curvilinear fibers.

В последнее годы широкое практическое применение находят композиционные материалы, армированные волокнами, расположенными произвольным образом в пространстве. Линейные волокна могут располагаться регулярно и нерегулярно, отличаться либо хаотической пространственной ориентацией, либо иметь определенную укладку в различных направлениях. Пространственное распределение волокон удобно задавать в общем случае с помощью плотности распределения сферических углов ϕ и γ , определяющих положение оси волокна в лабораторной системе координат (рис. 1). При этом следует иметь в виду, что подобное распределение может быть как дискретным, так и непрерывным. Рассмотрим различные типы армирования материала волокнами.

Рис. 1. Задание ориентации линейных волокон с помощью сферических углов

Если непрерывное распределение волокон не имеет преимущественной пространственной ориентации, то соответствующая плотность распределения f ( ϕ , γ ) по верхней полусфере проекций имеет вид

1π

f ( ϕ , γ ) = sin γ , 0 ≤γ≤ , 0 ≤ϕ≤ 2 π , 2 π               2

с условием нормировки

2 л/ 2

J J f ( ф , Y d Ф d Y = 1.

В случае, когда волокна в композите ориентированы по нескольким дискретным направлениям, плотность распределения f ф , у ) может быть представлена в виде суммы импульсных 5 -функций Дирака с весовыми коэффициентами, равными объемной доле волокон p k с соответствующей ориентацией:

f (Ф, y)=L Pk 5(Ф — Ф k )5(Y-Y к).

k

Так, при армировании волокнами, расположенными вдоль главных направлений, и волокнами, равнонаклоненными к координатным осям, функция плотности распределения имеет следующий вид:

f ⁽Ф, Y ) = P 1 ⁵ ( фДУ ^- П J + P 2 Д Ф^- ПД Y ^- П j + P 3 ⁵ ( ф^{) 5 (}У^{) +} оГ    п\д а / -\/ а

+ p 4 51 ф- — 15 ( у-у ) + p 5 51 ф + — 15 ( у-у ) +

( 3п\/              3п\/

+ p 6 51ф + — 15 ( у-у ) + p 7 51ф- — 15 ( у-у )

*

где у

= arctgV2.

На основе математических моделей и метода локальности [1] производим вычисление коэффициентов упругости и податливости материала в зависимости от структуры и текстуры композита, в том числе и сложноармированных материалов.

Начальным этапом проектирования конструкций из неоднородных материалов является исследование их напряженного состояния, что предусматривает знание полного набора всех упругих постоянных. Как известно, количество независимых упругих постоянных определяется симметрией материала, и экспериментальное определение всех постоянных не всегда бывает возможным в силу особенностей геометрии элементов конструкции и технологии их изготовления.

Традиционным методом определения деформационных характеристик пространственно-армированного композита по известным механическим свойствам его компонентов является метод осреднения модулей упругости отдельных однонаправленно-армированных элементарных объемов в модели композита.

Компоненты тензора упругости c(n) определяем по правилам преобразования ijkl компонентов тензора четвертого ранга

( n )                       *

c jjili = l ip l jq l kr l Is c pqrs ,

*

где c pqrs – компоненты тензора упругости однонаправленно-армированного композита с тем же объемным коэффициентом армирования; lip – косинусы углов между главными осями симметрии пространственно-армированного композита и осями локальной системы координат, связанной с направлением армирования элементарного объема.

На первом этапе определим упругие макроскопические характеристики однонаправленно-армированного композита. В силу предположения об эргодичности рассматриваемой модели осреднения по объему композита и ансамблю случайных ориентаций совпадают, что позволяет при вычислении упругих макроскопических характеристик пространственное распределение волокон описывать с помощью плотности распределения сферических углов, задающих положение случайно ориентированного волокна в лабораторных осях координат. Операцию осреднения по множеству ориентаций проводим с использованием сверток трансверсальноизотропного тензора c_pqrs по двум индексам, являющихся тензорами второго ранга, где 5 у - символ Кронекера.

с pqrr prqr

- ( c 1111	* + c 1122	* + c 1133	) + ( c 3*333
f 3 * < 2 1111	* ■^ c 1122	* + c 2323	) r * 1 + 1 c 3333

+ c 1133

3_{* 2} c ₁₁₁₁

c ₁₁₁₁

+ c 2323

^С 1122 ⁾§ p 3 § q 3 ,

+ 2 ^С 1122 l§ p 3 § q 3 ’

На этапе осреднения вводим понятие параметров армирования, которые определяются как средние значения направляющих косинусов второй и четвертой степени.

^А 1 ^— ( l в)’ ^А 2 ^— l 2 23 У ^А 3 ^— ( l 323 ), ^А 4 ^— ( l 13 )’ ^А 5 ^— ( l 23 )’ ^А 6 ^— ( l 33) "

Из шести параметров армирования независимыми являются только пять, так как в силу условия ортогональности существует зависимость вида

А1 + А 2 + А 3 = 1.

Компоненты тензора макроскопических упругих характеристик представимы в виде c11

****

= c 11 - ( 2 c 1 + 4 c ₂ ) А 1 + c ₃ А 4 ,

****

^c 22 ^{— c} 11    ( ^{2 c} 1 ^{+ 4 c} 2 ) ^А 2 ^{+ c} 3 ^А 5 ’

****

c 33 = c_n - ( 2 c 1 + 4 c 2 ) А 3 + c 3 А ₆

c 23

c ₁₃

c ₁₂

c 44

c 55

c 66

*

• —    ^c 13

*

^{— c} 13

*

• ^{—    c} 13

*

• ^{—    c} 44

*

• ^{—    c} 44

*

• ^{—    c} 44

⁺ ( ^c 1* ^{- c} 3* ) ^А 1 ⁺ ( ^c 1* ^{- c} 3* ) ^А 2 ⁺ ( ^c * ^{- c} 3* ) ^А 3 ⁺ ( ^c 2* ^{- c} 3* ) ^А 1 ⁺ ( ^c 2* ^{- c} 3* ) ^А 2 + ( c ₂ * - c 3* ) А 3

*

+ ^3 (1 + А 4 -А 5 -А 6 )’

*

+ 723-(1 + А 5 - А 6 - А 4 ),

*

+ ^3 ( 1 ^{+ А} 6 ^{- А} 4 ^{- А} 5 ) ’ *

c

+ ^ (1 + А4 - А 5 - А 6 )’ *

+ ^^ ^{( 1} + ^А 5 ^{- А} 6 ^{- А} 4 ⁾ , *

c

+ ^3 (1 + А 6 - А4 - А 5 )"

Аналогичным образом определены компоненты тензора податливости.

Таким образом, проблема прогнозирования упругих характеристик пространственно-армированных композитов сводится к определению параметров армирования по данным о характере пространственного распределения армирующих волокон.

При непрерывном пространственном распределении прямолинейных волокон в общем случае параметры армирования определены с помощью соотношений

П 2 п 2

П 2 п 2

А 1 = J j cos² ф sin² у • f ( ф , у ) d ф d y , A 2 — j J sin² ф sin² у • f ( ф , у ) d ф d у ,

П 2 п 2

A3 = j j cos2 у • f (ф, у)dфdу, п 2п 2

П

2 п "2

A 4 = j j cos⁴ ф sin⁴ У • f ( ф , у ) d ф d Y ,

П

2 п ₂

A 5 = j j sin⁴ ф sin⁴ у • f ( ф , у ) d ф d у , А б = j j cos⁴ у • f ( ф , у ) d ф d y .

Если волокна в

композите распределены равновероятно, то параметры

армирования принимают следующие значения:

^А 4 — ^А 5 — ^А б

.

А1 — А 2 — А 3 — 3,

В случае, когда волокна в композите ориентированы по нескольким дискретным направлениям, параметры армирования заданы равенствами

А1 — 2 Pk cos2 ф k sin2 У к , А 2 — 2 Pk sin2 ф k sin2 У к , kk

А з— 2 Pk cos2 у k, А 4— 2 Pk cos4 ф k sin4 у k, kk

А 5— 2 Pk sin4 ф k sin4 у k,А б— 2 Pk cos4 у k.

kk

Так, при армировании волокнами, расположенными вдоль главных направлений, и волокнами, равнонаклоненными к координатным осям, получены следующие параметры армирования:

^А 1 ^— P 1 + 3 ( P 4 ⁺ P 5 ⁺ P б ⁺ P 7 ) ,

^А 2 ^— P 2 ⁺ 3 ( P 4 ⁺ P 5 ⁺ P б ⁺ P 7 ) ,

^А 3 ^— P 3 ⁺ 3 ( P 4 ⁺ P 5 ⁺ P б ⁺ P 7 ) ,

^А 4 ^— P 1 ⁺ 9 ( P 4 ⁺ P 5 ⁺ P б ⁺ P 7 ) ,

^А 5 ^— P 2 ⁺ 9 ( P 4 ⁺ P 5 ⁺ P б ⁺ P 7 ) ,

^А б ^— P 3 ⁺ 9 ( P 4 ⁺ P 5 ⁺ P б ⁺ P 7 ) .

Значительные трудности возникают при моделировании и расчете пространственно-армированных композитов, когда волокна имеют искривления. Как правило, при этом рассматриваются упрощенные модели, в которых криволинейные волокна заменяются прямолинейными волокнами конечной длины с достаточно грубой аппроксимацией реального пространственного распределения.

Предлагаемый метод позволяет произвести эквивалентную замену криволинейных волокон на статистическую систему коротких волокон, имеющих ту же плотность распределения, на основе принципа локальности [2]. При этом параметры армирования вычислены по формулам

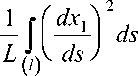
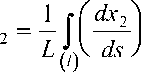
ds ,

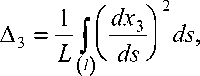
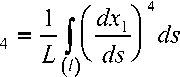
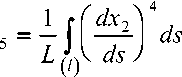
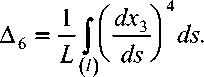
Для иллюстрации рассмотрим вычисление параметров армирования композита со спиральными волокнами и композита, армированного тканью полотняного плетения.

В случае, когда композит армирован волокнами, имеющими вид спирали, расположенной вдоль оси Ox 3 , где r – радиус навивки спирали, h – ее шаг, параметры армирования следующие:

л

^А 3  ----¹---Г

^{1 + 4 п2}h

, А

V

„ 2 _А 2

1 + 4 п ²

h ² )

, ^А 1 - ^А 2 -

/

1 + 4 п V

2 4 h ^{2 7}

,

л

А 4 - А

- 3

1 - 2

V

+

¹ + ^{4 п} V f ^{1 +} 4 п ² - 2 ]

V h ) )

.

Для композита, армированного тканью полотняного плетения с одинаковым содержанием и характеристиками волокон долевого и уточного направлений при моделировании волокон дугой окружности радиусом r и длиной хорды l , имеем

А 1

1 sin 2а .           .     1 sin 2а

---, А₂=А[ , А₃=- +------ , 4    8 а ^{2    1}         2    4 а

3 sin 2 а

16    8 а

sin 4а                3  sin 2а sin 4а +

32 а

+------, А₅ =А₄ , А₆ = - +------

64 а     ^{5    4 6} 8    4 а

Как правило, анизотропию упругих свойств материала связывают с зависимостью модуля Юнга и коэффициента Пуассона от направления. В плоскости Ox 1 x 2 модуль Юнга определяется соотношением

E-1 (а) = 5 11 cos4 а + 5 22 sin4 а + (5 66 + 2 s12 )cos2 а sin2 а, где а - угол между направлением растяжения и соответствующей осью.

Угловая зависимость коэффициента Пуассона в плоскости Ox 1 x 2 ортотропного материала может быть найдена как изменение отношения упругих деформаций по ширине и длине растягиваемого образца. Угловая зависимость коэффициента Пуассона при этом находится из выражения

^{v ( a )} =

5 12 + ( 5 ц + ⁵ 22 - 2 S 12 - s 66 ) cos² a sin² a

511 cos4 a + s22 sin4 a+ (2s12 + 566 )cos2 a sin2 a x1                                           x1

МПа

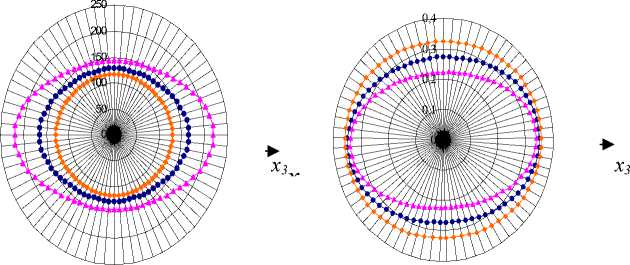
30%   60%   10%              30%  60%   10%

Рис. 2. Анизотропия модуля Юнга и коэффициента Пуассона для медной матрицы, армированной вольфрамовыми спиральными волокнами

Анизотропия модуля Юнга и коэффициента Пуассона для медной матрицы E m =1014 МПа, V ” =0,36, армированной вольфрамовыми спиральными волокнами Е =400 МПа, v ^f =0,045 [67] с c f =0,6, c f =0,5, c f =0,1, при угле навивки спирали 75 0 представлена на рис. 2.

При детерминистическом микроструктурном подходе основной проблемой является аналитическое построение решения для определения напряженно-деформированного состояния неоднородной среды. Часто основной задачей армирования является получение изотропного или трансверсально-изотропного материала. Из предложенного аналитического способа прогнозирования упругих свойств пространственно-армированных композитов следует, что разным схемам армирования могут соответствовать материалы с одинаковым набором упругих постоянных. Для этого необходимо выполнение условия равенства соответствующих параметров армирования.